例谈小学数学教学中如何培养学生的 质疑、应变和创造能力

林洪春 周立新

摘  要：小学数学是学生进入数学领域的基础阶段。这个阶段主要以熟记计算公式和运算法则以及大量机械重复训练来巩固所学知识。这个时候学生理论基础相对薄弱，自主分析意识和独立思考能力相对不足。对老师盲从，对课本例题抱住不放，解决问题时极易犯“教条主义”错误，不知变通，不善创新。长此以往，不利于学生理性素养的塑造和形成。

关键词：质疑;应变;创新;发散

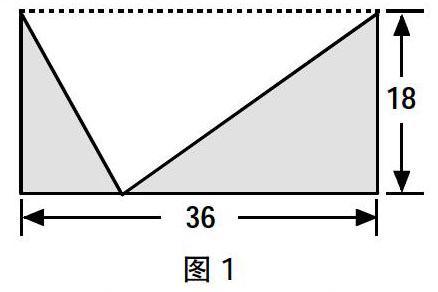
苏教版小学《数学》五年级上册26面第七題，有一个求面积的几何图形，要求涂色部分的面积。

这道题看似简单，实则大有文章。果然，学生自行解答时差不多都是千篇一律的差错：36×18=648，648×2=1296。要么就是束手无策，甚至怀疑题目给的已知条件不足。笔者针对这种普遍的错误，借题发挥，因势利导，引发学生质疑并借机培养学生的变通能力。

一、不拘泥于既定成型的定理公式，而要通晓并且运用定理的推导过程

在这个问题中，学生会产生困惑，究其原因主要是不会变通，死抠三角形的面积计算公式：三角形面积=底×高÷2。学生形成思维定式：要求出三角形的面积，就一定要知道三角形的底边长度和高度，然后代入公式求值。殊不知，学生准确牢记并忠实于三角形的面积公式，有时反而让思想受到束缚。这时，如果教会学生质疑：求出三角形的面积非要知道三角形的底边长和高度吗？三角形的面积仅仅是底边长与高度相乘的一个积吗？如果学生在面对权威定义公式时能够发出质疑，就会明白：面积是反映图形占据平面大小的一个量，并不单纯是一个乘积;三角形的面积公式是根据与其等底等高的平行四边形的面积的一半推导出来的。如此，学生便会茅塞顿开：根本没必要知道两个涂色三角形的底和高分别是多少，也不必先行分别求出两个涂色三角形的面积，再相加。只需要抓住“三角形的面积是与其等底等高的平行四边形的面积的一半”就可以另辟蹊径，快刀斩乱麻地解决问题。从整体看，图形为一个长方形，而挖去的空白三角形刚好与长方形等底等高。因此，空白三角形的面积是长方形的面积的1/2。于是，顺理成章得出余下涂色部分面积为长方形面积的1/2。局势一下子便明朗了，列式为：36×18×1/2=324。

二、能利用已有公式，根据题目形式临时创造出适用的特殊公式

苏教版小学《数学》五年级下册第111面第11题：

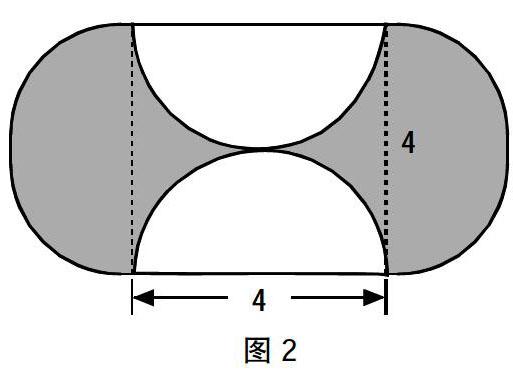
对于这个图形，要求的涂色部分都是不规则的图形，没有具体公式可言。为了顺利求出目标图形的面积，只能利用切分拼凑法，借助规则图形的面积计算公式创造出临时的适用公式。

如图2，涂色部分是不规则图形，先切分再叠加。左右两边为两个半圆，合起来算一个圆形，根据圆形的面积计算公式：

2×S半圆=S圆=πr2→S圆=π（D/2）2→S圆=π（4/2）2→S圆=4π。

中间剩余部分为两个不规则图形：

2×S不规则=S正-2×S半圆=S正-S圆。

再把两部分相加得出：

S涂色=S圆+（S正-S圆）=S正=4×4=16。

在这个图形的分析解决中，充分利用了已有公式之间的组合变形，得出新的临时公式，经过一些抵消运算后不断简化，最后得出一个极为简单的结论：S涂色=S正，顺利地把不规则图形面积计算转换为规则图形面积计算。

三、创造性化用已有运算定律来处理简便计算

在简便计算中，为了运算的便捷，往往需要应用学到的运算定律，这些运算定律都是对运算性质的高度总结。但是，课本上提到的运算定律十分有限，主要集中在加法和乘法上。如加法交换律、加法结合律、乘法交换律、乘法结合律、乘法对加法的分配律。这些运算定律不足以解决所有简便计算问题，这就需要我们教会学生“创造性套用”。通过知识迁移、核心规律“移植”等，创造性运用。

如由“加法交换律”可以衍生出“加减交换律”“减法交换律”。即a+b-c=a-c+b（在一个没有括号的加减混合运算中，交换加数和减数的位置以及运算顺序，结果不变）;a-b-c=a-c-b（在一个连减算式中，交换两个减数的位置，差不变）。

学生对原有的运算定律不能只掌握其“形”，更要领悟其“神”，才能创造性、变通性地应用其他运算。如将“乘法对加法的分配律”变通性地应用于减法，形成所谓的“乘法对减法的分配律”，同样具备合理性和逻辑性：a×（b-c）=（a×b-a×c）（一个数与两数之差相乘，可以先分别求出这个数与被减数、减数的乘积，再相减）。

依据“加法、乘法结合律”可以创造出“加减结合律”和“除法结合律”：a+b-c=a+（b-c）（在一个没有括号的加减混合运算中，先求出其中一个加数与减数的差，再与第一个加数进行运算，结果不变）;a÷b÷c=a÷（b×c）（在一个连除运算中，先求出几个除数的积，再与被除数相除，商不变）。

总之，要想增强学生的理论基础，提升学生的自主分析意识和独立思考的能力，培养和塑造学生的理性思维素养，就要让学生学会质疑、变通和创造。书中的定理、例题适用范围有其局限性，老师传授的经验带有鲜明的特性烙印。只有不迷信、不盲从，内化、吸收一些数理定律，才能真正做到活学活用、融会贯通。这样，在遇到疑难题型，没有现成的公式模板可以借鉴套用的时候，理应运用上述方法做出大胆尝试，因为“他山之石可以攻玉”。