变换思维角度:解决问题的有效策略
2018-01-03王文清
王文清

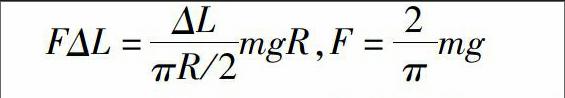

【内容摘要】新一轮课程改革对学生思维能力的培养提出来很高要求。如何结合物理学科培养学生的科学思维是需深入研究的问题。本文从日常教学案例着手,尝试引导学生从转变研究方向、静态动态转化、合理建立坐标、巧妙应用对称等方面,变换思维角度,有效解决问题,培养学生发散思维和求异思维,从而提升学生的核心素养。
【关键词】思维 策略 解决问题 核心素养 物理学科
即将启动的以学生学科核心素养培养为目标的新一轮课程改革,对培养学生科学思维提出了很高要求。通过物理学科的学习要求学生“具有批判性思维的意识,能基于证据大胆质疑,从不同角度思考问题,追求科技创新”。当然,创新离不开求异思维和发散思维的培养,思维的过程就是创新能力和创新精神培养的过程。
一、 一个实验引发的思考
在“超重与失重”的教学中,为了让学生更好地理解超重与失重现象,笔者设计了这样一个问题:一个人站在磅秤上,不借助其他工具,怎么样才能使磅秤的读数最大?几乎所有的同学都采取了同样的方法:人先蹲下,然后快速站起。站起时的加速度越大磅秤读数的增加量也越大。然而,有一位同学却采用了另一种方式:他先站直不动,接着快速下蹲,利用向下减速过程中的超重现象使磅秤的读数增加。他这种不同常人的方式最终赢得了比赛。
这个同学解决问题的思维方式引起了笔者的思考:从不同的角度考虑同一个问题时,常常能发现一些易被忽视的东西,而其中包含了解决问题最重要的要素;鼓励学生从不同的思维的角度来研究同一个问题,不仅对学生解题能力的培养有好处,更重要的是学生在问题研究中增强了创新意识,获得了创新精神。
二、 应用变换思维角度解决问题的实例分析
在平时的教学中,笔者总是有目的地创造机会,让学生展示他们在研究问题中表现出的创新能力和创新精神。下面是应用变换思维角度的策略来解决问题的一些实例分析。
1.转变研究方向,寻找问题突破
案例1:线上拴一小球,从水平位置A由静止释放。在小球从水平位置A运动到竖直位置B的过程中,当线与竖直方向的夹角θ为何值时小球的竖直分速度最大?常规的思路是,根据机械能守恒定律得:mglcosθ=12mν2所以,ν=2glcosθ。竖直方向的分速度νy=νsinθ=2glcosθsin2θ,当cosθsin2θ取最大值时,竖直方向的分速度νy有最大值。然而,求解cosθsin2θ的极值需要一定的数学技巧,问题陷入了困境。这时,启发学生变换思维的角度,研究竖直方向的分速度变化的原因。经过分析发现:前半个过程,由于重力大于绳子拉力的竖直方向的分量即:mg>Tcosθ,所以竖直方向处于加速状态,竖直方向的分速度νy不断增大;后半個过程,绳子拉力的竖直方向的分量大于重力,Tcosθ>mg,所以竖直方向处于减速状态,竖直方向的分速度νy不断减小。当mg=Tcosθ时, νy有最大值。
解决这个问题的关键在于,当从竖直方向的分速度 的表达式直接分析陷入困境时,变换思维的角度,从受力分析着手研究竖直方向分速度 变化的原因,找到了解决问题的突破口。
2.静态动态转化,抓住问题要害
案例2:一质量为m的均匀链条,绕在一光滑的1/4圆柱上,用一水平拉力作用,处于平衡状态。求:一水平拉力F的大小。这是一个关于物体平衡的问题。开始似乎很难找到解题的切入口。当变换思维的方法,从另一个角度分析时发现了解决问题的切入口。假设链条在拉力F的作用下向左缓慢地移动了很小的一段距离ΔL,则底部的链条将上升了ΔL。通过这样模型变换后,把原来的静态问题转化成了一个动态问题。当链条在拉力F的作用下移动了很小的一段距离ΔL过程中,相当于整个链条其它部分没动,圆柱体底部的链条上升了R。对整根链条应用能量守恒定律:
FΔL=ΔLπR/2mgR,F=2πmg
问题马上找到了答案。由于根据系统能量守恒定律进行求解抓住了问题的要害,题目求解简洁明快。当告诉学生上述方法是物理学中经典的思想——虚功原理时,他们感受到创造性学习的成功带来的快乐。
3.合理建立坐标,简化问题研究
案例3:从倾角为θ的斜坡顶端以初速度ν0水平抛出一小球,不计空气阻力,若斜坡足够长,则小球抛出后离开斜坡的最大距离H是( )。
(A)ν022g
(B) ν02sin2θ2g
(C)ν02sinθ2g
(D) ν02tanθsinθ2g
如果采用通常的坐标建立的方法,水平方向为X轴,竖直方向为Y轴,则计算不仅麻烦,还需要一定的技巧。
4.巧妙应用对称,深化问题认识
案例3:所示为白炽灯L1(规格为“220V 100W”)和L2(规格为“220V 60W”)的伏安特性曲线,根据该伏安特性曲线可以确定将L1、L2两灯串联接在220V电源上时,两灯消耗的实际实际功率分别为多少?
在这个问题中由于白炽灯是非线性元件,其伏安特性曲线不能用解析式来表示,所以无法用公式直接求解。这种情况下白炽灯的工作状态如何确定?是问题解决的关键。这个问题的求解,有学生想到了逐步逼近的方法。因为串联电路中电流强度相等,用一直尺与横坐标平行画出一系列直线,当L1与L2两灯的电压之和为220V时,直线与两伏安特性曲线的交点即为问题的解。
变换思维的角度是解决问题的一种有效策略。在实际解决问题的过程中,当常规的思路陷入困境时,如果能及时地变换思维的角度,往往能产生意想不到的效果。更重要的是,寻找独特的思维角度的过程,正是对学生创新能力和创新精神培养的过程,他们在创造性学习的过程中体会到成功带来快乐的同时,更坚定了对科学探索持久的热情,逐步形成了学生发展终身受用的核心素养。
【参考文献】
[1] 教育部.普通高中物理课程标准(实验)[M].北京:人民教育出版社,2014(7).
[2] 赵国庆.思维可视化[M]. 北京: 北京师范大学出版社,2016(7).
(作者单位:安徽省安庆第一中学)endprint
