基于贝叶斯方法的Meta-分析

张珍， 赵强

(山东师范大学数学与统计学院, 山东 济南 250014)

基于贝叶斯方法的Meta-分析

张珍， 赵强*

(山东师范大学数学与统计学院, 山东 济南 250014)

稀疏数据; 贝叶斯模型; Jeffreys分布; 链接函数; Meta-分析

1 引言及预备知识

1976年，英国心理学家Glass[1-2]提出Meta-分析，这是以综合已有发现为目的, 对单个研究结果的集合的统计学研究方法。Meta-分析又称作荟萃分析、整合分析、汇总分析, 是对具有相同研究题目的多个研究进行综合分析的一系列过程, 其中包括提出研究问题、制定纳入和排除标准、检索相关研究、汇总基本信息、综合分析并报告结果等[3]。

到目前为止, 针对稀疏数据的合并, 大致分为两个方向: 一种是对稀疏数据进行填补, 即对试验中存在0案例的试验进行连续性修正; 另外一种是无需进行连续性修正, 运用贝叶斯模型直接对各个试验结果进行分析。

2 Meta-分析中的贝叶斯模型

贝叶斯统计学的基础是贝叶斯公式和贝叶斯定理，贝叶斯公式是基于条件概率的定义和全概率公式推导而来[4]， 因此贝叶斯公式的实践形式如下: 设试验E的样本空间为S,A为E的事件，B1,B2,…，Bn为样本空间S的一个划分, 且p(A)>0,p(Bi)>0,i=1,2,…,n，则由条件概率的定义及全概率公式可得:

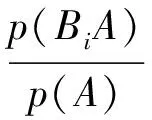
贝叶斯公式密度函数形式如下: 设x=(x1,x2,…,xn)是来自某总体的样本, 该总体的概率密度函数为p(x|θ),当给定一组观察值x=(x1,x2,…,xn)时,θ的条件概率分布为

即在样本x=(x1,x2,…,xn)下θ的后验分布。其中，π(θ)是参数θ的先验分布。

为样本x=(x1,x2,…,xn)的联合条件密度函数, 也即似然函数。

为x的边缘密度函数, 是一个与θ无关的量。

2.1 先验分布为Jeffreys无信息先验的贝叶斯统计模型

而在0～1之间的不可观察的变量x的贝叶斯模型如下:

其中，为了完善Meta-分析中贝叶斯模型的计算公式, 我们需要一个链接函数π(θi|θ), 注意这个条件分布必须兼容早先给的π(θi)和π(θ),也就意味着二维分布π(θi,θ)=π(θi|θ)π(θ)必须满足积分公式[5]

通常π(θi,θ)可能依赖于不确切的超参数t。 这里考虑内在先验分布类

{πIJ(θi,θ|t),t≥1}，

经验证

可用作模型的链接函数, 上式是一个单变量Beta密度的混合。因此, 可以用统计软件实现。例如R、Mathematic。 经过计算, 可以得出在给定t下,θi和θ之间的相关系数如下:

这是一个关于t的递减函数[6]。

考虑一个有不同中心的k个相互独立的随机临床试验结果, 用(xi,ni),i=1,2,3,…,k表示可观察到的多中心数据集。θi表示数据中心的概率效应, 即xi～B(θi,ni)。 接下来的计算公式运用θi的似然函数和链接分布可得

在给定t下, 参数θ的似然函数可有下式表达出来:

其中，P(x)表示变量x的似然函数。假设(xi,ni)对i=1,2,…,k相互独立, 在给定θ的条件下,θi在θ下条件独立。然后对整个数据集有参数θ的似然函数如下:

令n=(n1,n2,…,nk),x=(x1,x2,…,xk),而在给定t下,θ的后验概率可由下式给出:

其中关于参数θ, 应用数据(x,n)包含所有的信息, 符号“∝”表示“正比于”, 注意正常化常数不能从其封闭形式中得到。这里需要一个简单的一维数值分析。关于变量X的预测分布, 在给定数据(x,n)和超参数t下, 可得

其中，X=0,1t≥1。

当X=1时, 上式得

注意, 处理组的试验成功时恰好有P(X=1|x,n,t); 并且观察到只有在0-1随机变量的情况下, 预测分布的变量和参数的后验期望一致。然而, 当随机变量超过两个值时, 这个情况将不会成立。

2.2 先验分布为更一般形式的贝叶斯模型的推广

满足条件; 这里,t是一个超参数. 运用θi的似然函数和链接分布可得:

类似2.1的计算过程, 关于变量X的预测分布, 在给定数据(x,n)和超参数t下, 可由下式得出:

其中，X=0,1，t≥1。当X=1时, 上式得

事实上, 处理组的试验成功时恰好有P(X=1|x,n,t), 而上面得到是关于θ的一组向量。

[1]GLASS G V. Primary,secondaryand Meta-analysis of research[J]. Educ Res, 1976, 5(10):3-8.

[2]YATES F. Contingency tables involving small numbers and the chi-squared test[J]. Supplement to the Journal of the Royal Statistical Society,1934，1(2):217-235.

[3]王丹,翟俊霞,牟振云,等. Meta-分析中的异质性及其处理方法[J].中国循证医学杂志,2009.9(10):1115-1118.

[4]COCHRAN W G. Problems arising in the analysis of a series of similar experiments[J]. Supplement to the Journal of the Royal Statistical Society,1937,4(1)102-118.

[5]MANTEL N,HAENSZEL W. Statistical aspects of the analysis of data from retrospective studies of disease[J].Journal of the National Cancer Institute,1959,22(4):719-748.

[6]MORENO E,VAZQUEZ-POLO E J,NEGRIN M A. Objective Bayesian meta-analysis of sparse discrete data[J].Stat Med,2014,33(21)3676-92.

[7]VAZQUEZ-POLO F J,MORENO E， Negrín M A, et al. A bayesian sensitivity study of risk difference in the meta-analysis of binary outcomes from aparse data[J]. Expert Rev Pharmacoecom Outcomes Res，2015，15(2):317-322.

Meta-analysisbasedonBayesianmethod

ZHANGZhen,ZHAOQiang*

(InstituteofMathematicsandStatistics,ShandongNormalUniversity,Jinan250014,China)

∶sparse data;Bayesian model;jeffreys distribution;link function;Meta-analysis

10.3976/j.issn.1002-4026.2017.06.019

2017-03-31

国家自然科学基金(11001155)

张珍(1991—), 女, 硕士研究生, 研究方向为应用统计。

*通信作者，赵强，男，副教授。E-mail:zhaoqstst@126.com

O211

A

1002-4026(2017)06-0115-04