求解可重入作业车间调度问题的改进离散微粒群优化算法
2018-01-03万婧
万婧
(山东省科学院海洋仪器仪表研究所,山东省海洋仪器仪表科技中心,山东 青岛 26600)
求解可重入作业车间调度问题的改进离散微粒群优化算法
万婧
(山东省科学院海洋仪器仪表研究所,山东省海洋仪器仪表科技中心,山东 青岛 26600)
本文针对可重入作业车间调度问题,对离散微粒群算法的搜索方式进行改进,混合一种变异机制,并结合Interchange邻域局部搜索机制,设计与开发有效的混合离散微粒群算法。通过实验仿真结果的比较,有力地证明了所提算法的有效性。
离散微粒群算法;局部搜索;作业车间
可重入作业车间调度问题(reentrant job shop scheduling problem,RJSP)是工业生产中的典型调度问题,是现代很多实际生产调度问题的简化模型,包括诸如半导体生产、超大规模集成电路设计与制造、物流运输、网络通信电路设计、电气布线等问题。可重入作业车间调度问题的求解难度很高,一直是学术界和工程界共同关注的重要课题。除混合的算法开发外,设计新颖的调度技术或将其他领域的优化算法推广到生产调度问题中同样是值得关注的课题。
1 问题模型
可重入作业车间调度问题通常描述如下:每个工件i在m台机器上要被加工R(i)次,R(i)是可变的;所有工件经过机器的顺序都是恒定的;任何时刻,每台机器只能加工一个工件,每个工件也只能在一台机器上进行加工。
C(πj,1,l(πj))=max{C(πj-1,1,l(πj-1)),C(πj,m,l(πj)-1)}+p(πj,1,l(πj)),j=1,…,R,
C(πj,k,l(πj))= max{C(πj-1,k,l(πj-1)),C(πj,k-1,l(πj))}+p(πj,k,l(πj)),k=2,…,m,
Cmax(π)=C(πR,m,l(πR)),
π*=arg{Cmax(π)}→min,
式中:m表示机器数,R表示n个工件中每个工件的重入次数,n表示工件数,π=[π1,π2,…,πR]是工件加工排序,πj∈{1,…,n}(j=1,…,R)表示排序π中第j个位置的工件,l(πj)表示工件πj在[π1,…,πj]中重复出现的次数,p(πj,k,l(πj)是工件πj第l(πj)次进入第k台机器的加工时间,C(πj,k,l(πj))是工件πj第l(πj)次进入第k台机器的完工时间,C(π0,k,l(π0))=0,C(πj,k,0)=0,k∈{1,…,m},优化目标是找到一个最优排序π*,使得对应的最早完工时间Cmax最小。
2 研究方法
针对可重入作业车间调度问题的求解方法,通常可分为精确方法、构造性方法、改进型方法和神经网络等。精确方法,如枚举法[1]、分支定界法[2]、动态规划[3]等,由于其计算存储量太过巨大,因此仅适用于求解小型种群规模问题。构造性方法通过一定的规则来构造问题的解,如Gupta法[4]、CDS法[5]、RA法、NEH法[6]、SL法等,此类求解方法可以快速寻找解的位置,以最快的速度找到最优解,但通常解的质量不优。改进型算法则是从若干已知解出发,对其周围邻域的不断深入探索,以及对当前解的替换来改进解的质量,如遗传算法[7]、模拟退火[8]、进化规划[9]、禁忌搜索[10]等。这些方法的优化效果十分可观,但不足之处在于,需要大量迭代,并且其算法操作顺序、参数和搜索结构要求十分严格,均需谨慎选取。
微粒群算法[11]是一种基于进化群体智能技术的新型算法,能够通过模仿鸟类的觅食行为,寻求最优解的过程就是鸟类觅食的过程。微粒群算法提供了每个个体在这个过程中的觅食规则,使鸟类觅食过程与整个粒子群的搜索过程能够做到有效的衔接,从而使其有效地应用于解决复杂的优化问题。
本文介绍了混合离散微粒群算法的具体实现过程。该算法采用混合离散微粒群算法对问题解空间进行有效快速的全局搜索,为避免对粒子的搜索陷入局部最优,我们引入了一种变异机制来改变算法的位置更新公式,使得其全局搜索能够更快更迅速地获得较优解存在的区域;进而采用插入法和两点邻域交换法来构造局部搜索,更加有效地在全局搜索得到的较优解邻域中进行更加细致的搜索,从而使得算法具有更强的搜索能力,为进一步获得优质解奠定了基础。
3 算法流程
3.1 解的编码
解的编码方式有基于工件的编码、基于机器的编码、基于随机键的编码等。在可重入作业车间调度问题中,最常用的编码方式则是直接采用工件的排序,故本文算法的编码规则采用基于工件的编码规则。
3.2 基于混合离散微粒群算法的全局搜索
混合离散微粒群算法的搜索过程是建立在微粒群算法的基础上的,在位置更新公式中加入了新的因素,后续实验表明该算法更加快速有效。步骤如下:
A、种群初始化:种群规模为M,采用随机方法产生初始化种群,直至初始解的数量达到种群规模的要求;
B、在给定的空间随机产生Ps-1个微粒的离散位置矢量,其中Ps代表群体规模,确定各微粒对应的加工顺序,并进行调度目标的评价;
C、采用位置更新公式更新所有微粒的位置。
首先声明,每个微粒对应着一个工件加工排序。
从各类文献的总结结果中得出,微粒群优化机制[11]可以这样理解:已经产生的第一代微粒基于自己伙伴的飞行经验不断调整自己的位置和速度,从而朝着最佳位置飞行,也就是说,微粒的新位置是其速度、自身最佳位置和群体最佳位置相互作用的结果,最终确定最佳位置。根据以上机制,我们可以得到如下位置更新公式


上述位置更新公式由三部分依次执行构成,下面逐一解释。
第一部分


第二部分

第三部分

为了避免陷入局部最优解,提高算法性能和搜索能力,我们在微粒的位置更新公式中作如下改进:

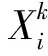
随机选取一个微粒的最佳位置所对应的最优值,与当前微粒最优值做比较,若当前微粒的目标值大于随机选取的微粒的目标值,则选用当前微粒,并取代随机选取的那个微粒最优位置对应的粒子。根据更新后的微粒,随机生成若干位置,把这些位置对应的值相互交换,得到新的微粒,再对其进行目标值的优劣比较,选择优者进入下一代的搜索。
3.3 局部搜索
对于车间生产调度问题,这里所提到的两种有效的局部搜索都是在文献中经常使用的。第一种是将工件排序中位置u与位置v之间的工件进行倒序排列(inverse(π,u,v)),第二种是交换工件排序中位置u和位置v处的工件(interchange(π,u,v)),实验证明,这两种局部搜索方法皆能够提高算法性能,帮助算法更快地找到最优解存在区域。因此,我们采用上述倒序操作(inverse)和交换操作(interchange)来构造局部搜索。所构造的局部搜索步骤如下:
步骤1:对于所选定的第i个个体的工件排序πi_0;
步骤2:扰动阶段
随机选择u和v两个位置,当u≠v时;πi=interchange(πi_0,u,v);
步骤3:探索阶段
Set loop=1; //设置循环体;
Do
随机选择u和v,当u≠v时; //选择u和v不同位置的工件;
令πi_1=inverse(πi,u,v); //执行inverse操作;
iff(πi_1) loop++; //继续循环,直到循环次数达到为止; While loop<(n*(n-1)); 步骤4:如果f(πi) 步骤5:将πi_0重新转换为Xi(t); //循环结束后,选择最优工件排序及调度目标值; 在上述步骤中,步骤2是扰动阶段,引导算法跳出局部最优,使其在不同区域进行探索。步骤3是对步骤2得到的邻域进行深入开发,得到更优解。从而有利于算法更快更有效地搜索存在不同优质解的区域,提高了混合离散微粒群算法的搜索与开发能力。 为了验证混合离散微粒群算法的有效性,我们采用随机生成不同规模的试验例子来测试混合离散微粒群算法的性能。有以下规模组合n*m*l。各个工件在各个机器上的每次重入加工时间服从[1,100]的均匀分布。最大完成时间C是整数。 每个工件的完成时间规定如下: 步骤1:对每个不同的问题p,随机生成工件排序。 步骤2:计算评价步骤1中的工件排序,得到目标值。 步骤3:针对每个测试例子,独立运行混合离散微粒群算法20次,将得到的结果进行比较研究。 以Delphi 7.0为开发环境,采用操作系统为Windows 7、CPU在Intel Celeron 2.40 GHz以上、内存256 MB以上、硬盘80 GB以上、显示器SVGA高分辨率彩色的PC。 通过一个实例演示。设置合理的算法参数,如算法的运行代数为200(设置范围为[5,1000]间整数),惯性权重系数W为0.5(设置范围为[0,1]间实数),认知系数C1为0.5(设置范围为[0,1]间实数),社会系数C2为0.5(设置范围为[0,1]间实数),设置“工件数”为10(设置范围为[1,100]间整数),“机器数”为5(设置范围为[1,20]间整数),“可重入次数”为3(设置范围为[1,10]间整数)。运行2种算法,即无局部搜索的DPSO算法(DPSO_noLS)和带局部搜索的DPSO算法(DPSO),可得如图1所示结果。 图1 DPSO_noLS和DPSO运行结果比较Fig.1 Operation results comparison between DPSO_noLS and DPSO 主界面右上半部分的曲线图形为相应算法第1至第200代每代最优个体(即截止当前代算法找到的最优个体)对应的适配值(即最大完工时间makespan)曲线,从曲线可知两种算法均能不断改进搜索质量,但DPSO算法对应的曲线下降更快,这验证了加入局部搜索是可行且有效的。主界面左上部分的两个文本框中分别显示两种算法运行200代中每代对应的最优值(即截止当前代算法得到的最小makespan),从中可知DPSO算法得到的每代最优值相对较小,只是由于加入了局部搜索,使得算法运行时间较长。主界面下半部分的文本框中显示了算法第1代和第200代的运行结果,包括第1代和第200代对应的最优值和工件排列。 本文提出混合离散微粒群算法DPSO,用于求解可重入作业车间调度问题。混合离散微粒群算法是学术界首个基于离散微粒群算法求解该问题的算法,有着巨大的影响力。混合离散微粒群算法利用改进的位置更新公式对问题解空间进行有效快速的全局搜索,并迅速准确地发现存在优质解的区域,同时采用基于倒序操作和交换操作的两种有效的局部搜索来针对存在优质解的区域进行深入搜索,提高了算法性能,在有限的时间内,加强了算法的搜索能力,提高了算法效率。 [1]PARPINELLI R S, LOPES H S. New inspirations in swarm intelligence:A survey[J] International Journal of Bio-Inspired Computation,2011,3(1):146-159. [2]马丁,陈庆新,毛宁,等.具有交货期约束带准备时间的平行机分批调度[J]. 计算机集成制造系统,2012,18(01):159-188. [3]WANG L, WANG S Y, XU Y,et al. A bi-population based estimation of distribution algorithm for the flexible job-shop scheduling problem[J] . Computers & Industrial Engineering,2012,62(4): 917-926. [4]汪慎文,丁立新,张文生.差分进化算法研究进展[J]. 武汉大学学报(理学版),2014,60(4): 283-292. [5]YANG X S. Flower pollination algorithm for global optimization[C]//International Conference on Unconventional Computing and Natural Computation. Berlin Springer,2012: 240-249.. [6]李修琳,鲁建厦,柴国钟,等.混合蜂群算法求解柔性作业车间调度问题[J].计算机集成制造系统,2011,17(7): 1495-1500. [7]吴尤可,王田.基于蚁群群体智能理论的创新政策扩散研究[J]. 科学学与科学技术管理,2014,35(4): 35-40. [8]ZHANG R, SONG S J, WU C. A hybrid artificial bee colony algorithm for the job shop scheduling problem[J] .International Journal of Production Economics,2013,141 (1) : 167-178. [9]WANG L, ZHOU G, XU Y, et al. An effective artificial bee colony algorithm for the flexible job-shop scheduling problem[J] .The International Journal of Advanced Manufacturing Technology,2012,60(1): 303-315. [10]王圣尧,王凌,许烨.求解混合流水车间调度问题的分布估计算法[J]. 自动化学报,2012,38(3): 437-433. [11]夏小翔.改进的微粒群优化算法[J].鄂州大学学报,2011,18(5): 5-7. Improveddiscreteparticleswarmoptimizationalgorithmtosolvethereentrantjob-shopschedulingproblem WANJing (ShandongTechnologicalCenterofOceanographicInstrumentation,InstituteofOceanographicInstrumentation,ShandongAcademyofSciences,Qingdao26600,China) ∶In this paper, by combining the existing discrete particle swarm optimization algorithm with a small but effective local search, an effective hybrid discrete particle swarm optimization algorithm was formed. This paper also discussed how to fuse the local search to optimize the discrete particle swarm. And the effectiveness of the proposed algorithm has been proved by the comparison of the simulation results. ∶discrete particle swarm optimization algorithm;local search;job-shop 10.3976/j.issn.1002-4026.2017.06.017 2017-01-03 青岛市市南区科技发展基金(2016-2-012-ZH ) 万婧(1989—),女,助理工程师,研究方向为海洋技术。E-mail:1066358426@qq.com TP301.6 A 1002-4026(2017)06-105-054 仿真试验比较

5 结论
