基于LMI的倒立摆滑模控制器设计

任鹏飞，赵玉顺，崔 勇，李雪健

(1.河南工程学院 电气信息工程学院，河南 郑州 451191;2.河南顺康机电设备有限公司,河南 郑州 450007)

基于LMI的倒立摆滑模控制器设计

任鹏飞1，赵玉顺2，崔 勇1，李雪健1

(1.河南工程学院 电气信息工程学院，河南 郑州 451191;2.河南顺康机电设备有限公司,河南 郑州 450007)

倒立摆是典型的欠驱动系统，针对其复杂非线性和存在不确定干扰的问题，提出了滑模控制器设计方案.以线性化模型为基础设计滑模切面，完成了对模型确定部分的控制设计，以及对不确定干扰的补偿输入.以线性矩阵不等式方法辅助完成滑模面和反馈增益的计算，避免了参数调试对设计经验的依赖.通过软件仿真和固高倒立摆测试对所提的控制方案进行测试，结果表明控制器有效实现了倒立摆的稳定控制.

滑模控制；欠驱动；倒立摆；线性矩阵不等式

倒立摆是多变量、强耦合的不稳定系统，被公认为是控制领域中验证控制策略的首选试验平台[1-3].该系统以唯一的拖动输入实现小车位置和摆杆角度的多变量控制，独立控制变量个数小于系统自由度个数，是典型的欠驱动系统.欠驱动系统在节约能量、降低造价、减轻质量、增强系统灵活度等方面都比完全驱动系统优越.由于系统的高度非线性、参数摄动、多目标控制要求及控制量受限等原因，而且它又足够复杂，所以欠驱动系统便于研究和验证各种算法的有效性[4].

由于倒立摆系统存在复杂非线性和不确定干扰，采用线性化的模型所设计的控制器通常无法获得较好的控制效果.例如,经典的PID需要在调试时反复试凑控制参数，而无法直接处理复杂系统.线性二次优化的LQR方法，其加权函数阵的选择需要依赖经验反复试凑，实时控制效果不理想.由于滑动模态可以进行设计且与对象参数及扰动无关，这就使得变结构滑模控制具有快速响应的特点，采用滑模控制方法可以有效地实现一类欠驱动系统的鲁棒控制[5-7].

为了优化倒立摆稳定控制效果，将滑模控制方法用于反馈控制器设计.利用滑模控制对参数变化及扰动不灵敏、不需要系统在线辨识、物理实现简单等优点，实现倒立摆小车位置和摆杆角度的控制优化.在滑模函数的设计中，需要考虑约束条件，在控制问题中转化为线性矩阵不等式约束的最优化问题.采用Matlab软件中提供的LMI工具完成求解计算，以得到反馈控制增益和滑模面所需要的正定矩阵.

1 倒立摆系统的欠驱动力学分析

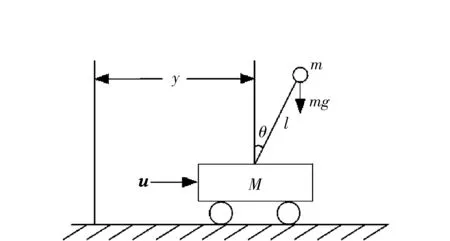
图1 倒立摆结构Fig.1 Structure diagram of inverted pendulum

小车倒立摆基本结构如图1所示.忽略空气阻力的影响并将摆杆视为刚体，以简化系统建模分析.利用牛顿力学方法可分别对摆杆和滑动小车进行运动分析，系统建模详细步骤见文献[2]，这里不再赘述.直接给出其动力学模型：

(1)

(2)

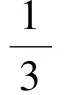
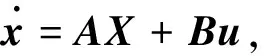
(3)

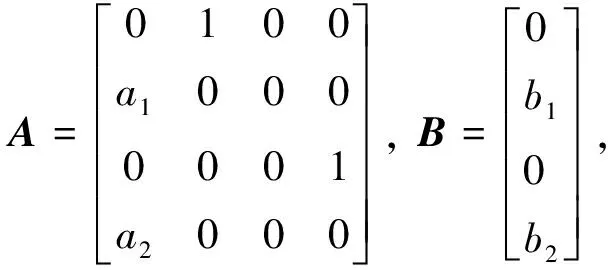
通过设计拖动力u的大小和方向，使小车移动到目标位置并保持摆杆倒立不倒.不失一般性，系统控制目标为x→O.

2 系统滑模控制器设计

基于式(3)的状态空间方程进行倒立摆系统的滑模控制器设计.考虑到不确定性和干扰f(x，t)，系统方程(3)可修正为

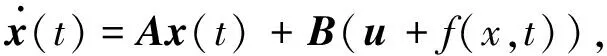
(4)

式中的干扰信号是有界的，记|f(x，t)|≤δf.

2.1 滑模控制器

定义滑模函数为s=BTPx.这里，P为4×4阶正定矩阵，通过P的合理设计实现s=0.这里先讨论滑模控制器的可行性，而正定矩阵P的计算将在2.2给出.

考虑不确定干扰信号，系统的控制输入包括两个部分：滑模等效控制ueq，提供控制系统所需的确定控制量；扰动补偿控制un，用来修正不确定干扰因素的不利影响.因此，设计滑模控制器为

u(t)=ueq+un，

(5)

式中的滑模等效控制和扰动补偿控制分别为

ueq=-(BTPB)-1BTPAx，

(6)

un=-(BTPB)-1[|BTPA|δt+ε0]sgn(s).

(7)

滑模控制器以实现s=0为设计目标，式(5)综合控制器设计的合理性可以通过Lyapunov稳定性理论加以说明.

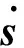
(8)

所以，

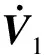
(9)

式(9)中Lyapunov函数的负定表明存在t≥t0，使得s=BTPx=0.

2.2 控制律的LMI辅助设计

采用LMI方法来设计滑模函数中的对称正定矩阵P.将控制律(5)写作

u(t)=-Kx+v(t)，

(10)

式中:v(t)=Kx+ueq+un.那么，系统方程(4)重新整理为

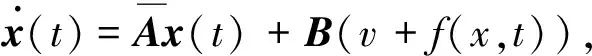
(11)

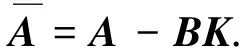
再取Lyapunov函数为V=xTPx，可得

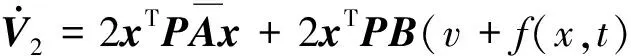
(12)

由式(8)和式(9)分析可知，存在t≥t0，使得s=BTPx=0，即sT=xTPB=0成立，所以有

(13)

(14)

取L=KP-1，则

AX-BL+XAT-LTBT<0.

(15)

整理为线性矩阵不等式，有

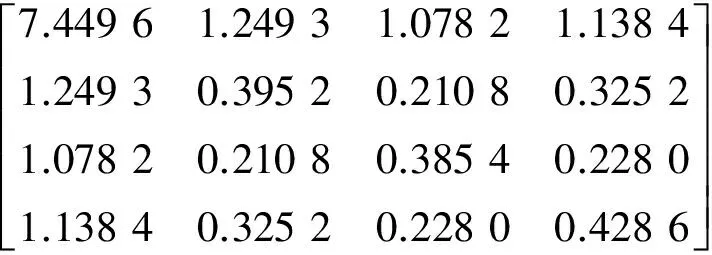
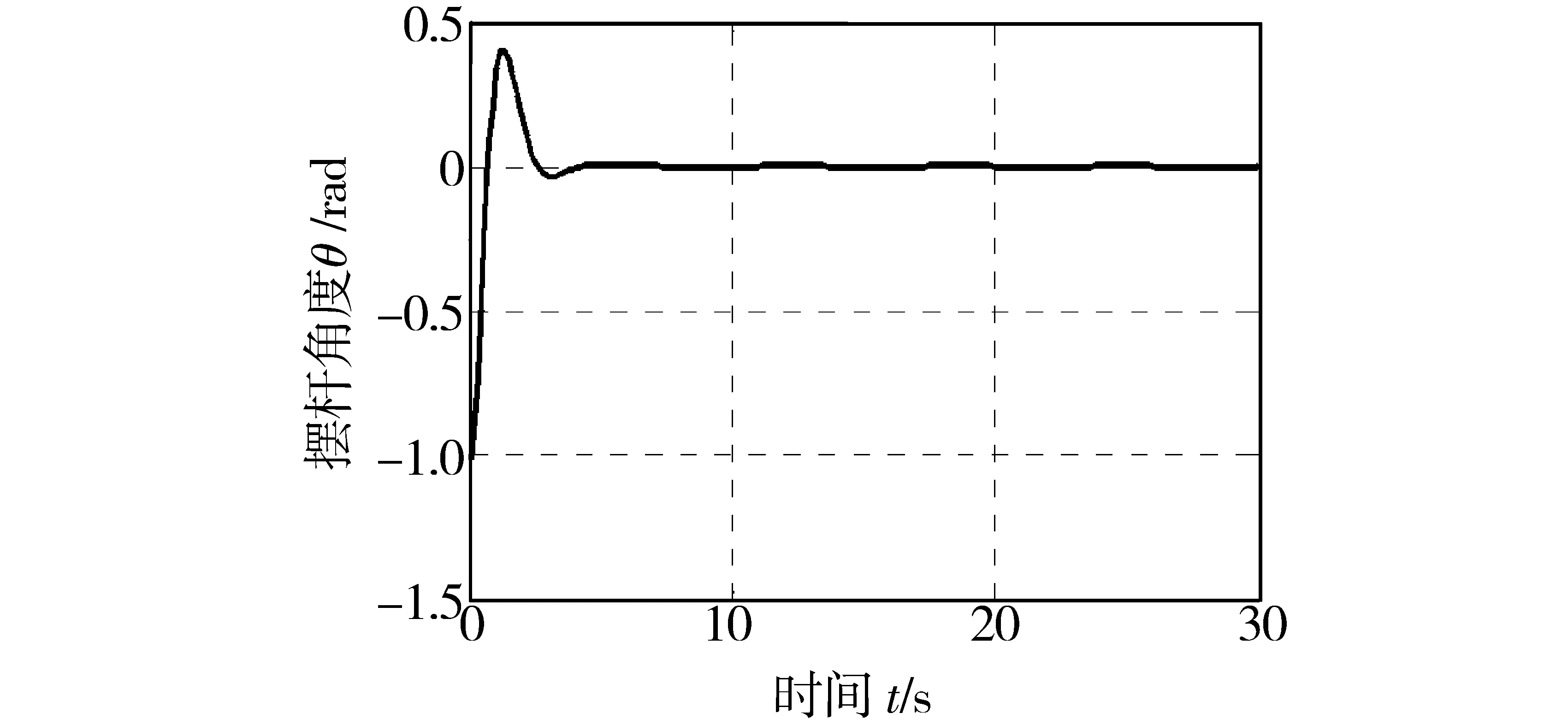
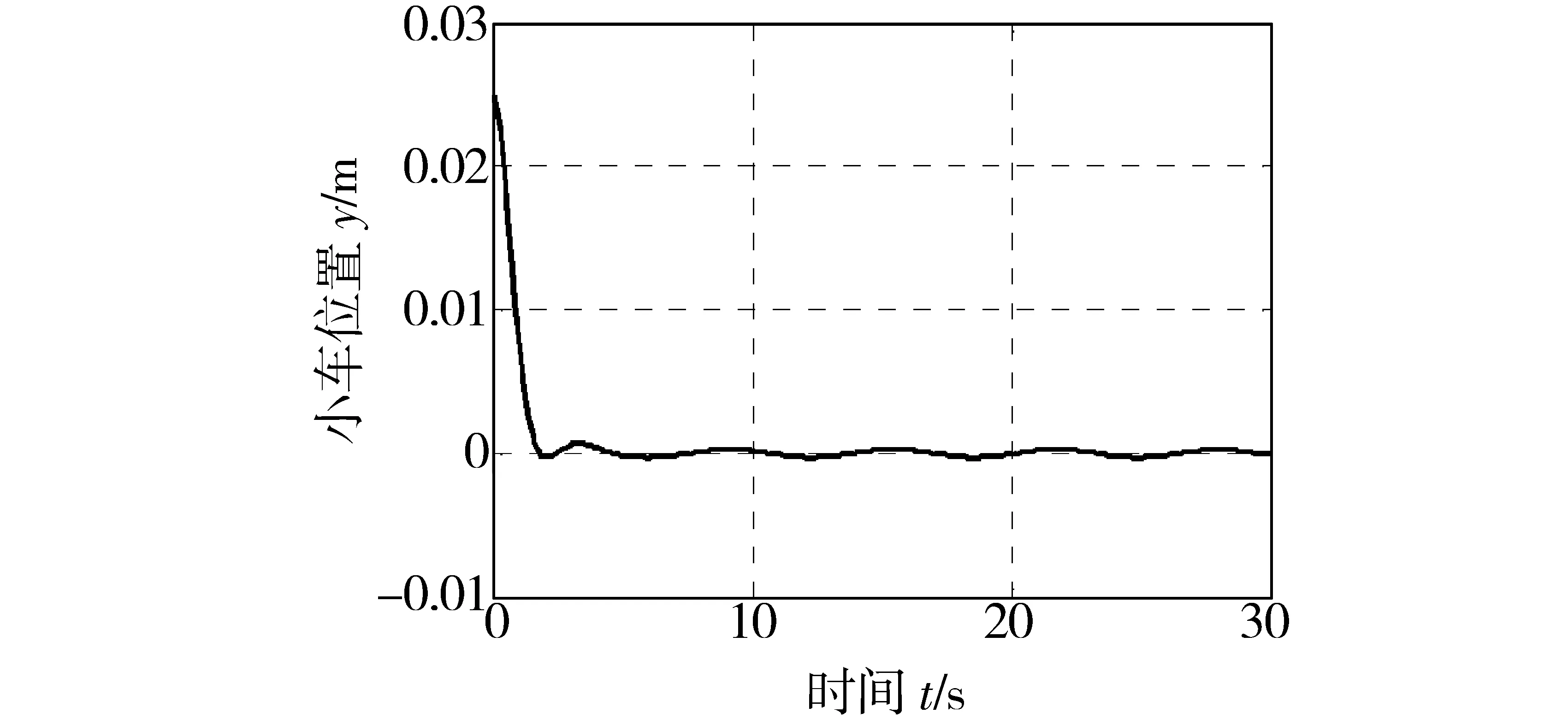
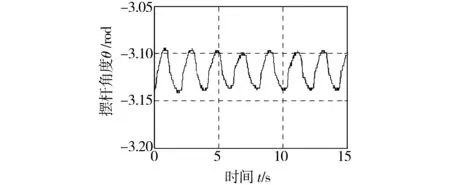
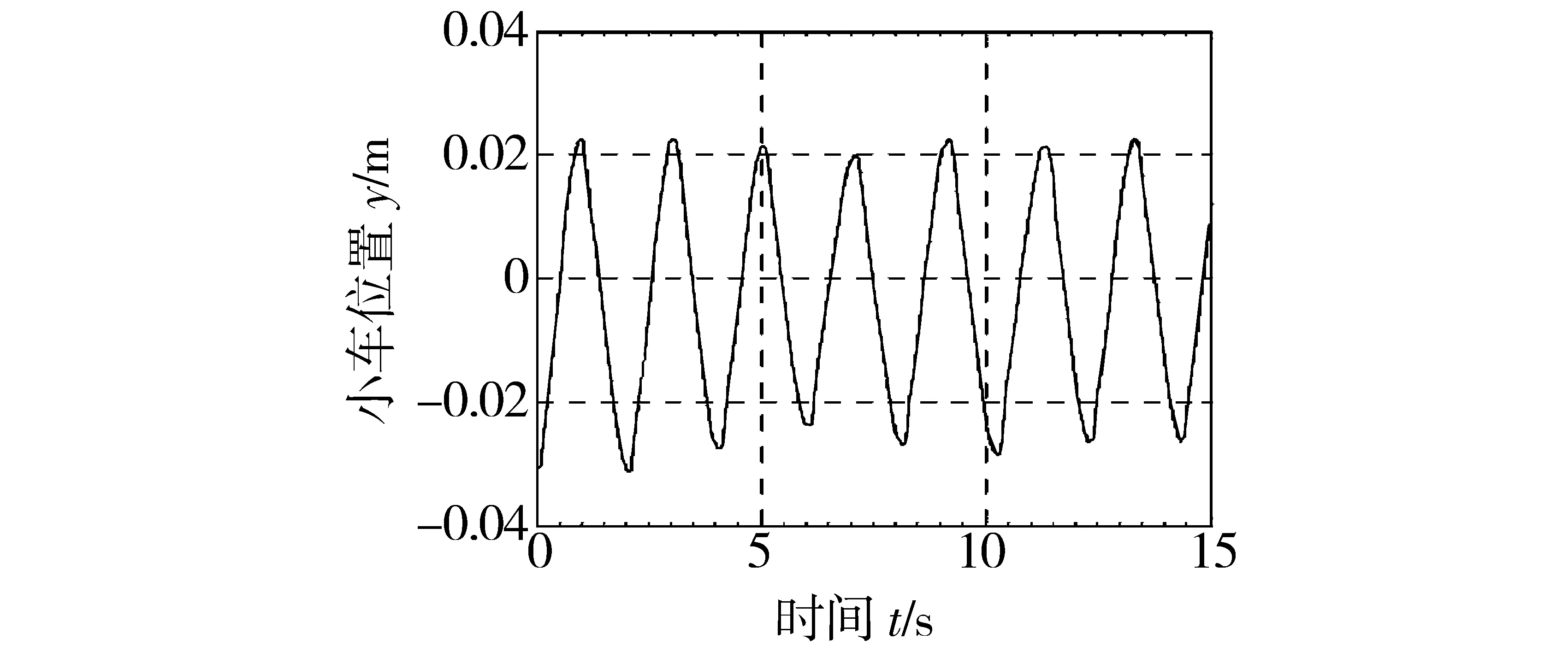
AX+XAT

(16)

利用Matlab的LMI工具箱进行辅助计算，可得到正定矩阵P和反馈控制增益矩阵K.设计过程中，为了保证P为对称正定矩阵，需要满足P=PT>0.

3 仿真及试验测试

采用滑模控制器，取δf=0.3，ε0=0.15.采用饱和函数代替切换函数，边界层厚度取Δ=0.05.这里需要指出，边界层厚度越小，控制效果越好，但同时又会使控制增益变大，抖阵增强；反之，边界层厚度越大，抖阵越小，但又会使控制增益变小，控制效果差.边界层的设置仅能保证系统状态收敛到以滑动面为中心的边界层内.可以通过较窄的边界层来任意地接近滑模，但不能使状态收敛到滑模.

利用LMI解算工具箱对式(16)进行计算，得到正定矩阵P和反馈矩阵K:

利用所得控制参数测算倒立摆小车的拖动输入，在Matlab/Simulink中进行仿真，得到小车的运动位置和摆杆的角度变化，如图2和图3所示.从仿真结果可以看出,摆杆角度和小车位置3 s后即到达目标位置并持续保持在目标值,仿真输出曲线存在小幅抖阵，波动幅值与滑模面切换和不确定干扰项的存在有关.

图2 摆杆角度仿真结果Fig.2 Simulation result of pendulum angle

图3 小车位置仿真结果Fig.3 Simulation result of pendulum position

图4 固高倒立摆实验平台Fig.4 Googol inverted pendulum

图4为固高倒立摆试验平台，由控制主机、运动控制箱和倒立摆机械部分组成.在Matlab仿真分析基础上，将所得控制输出信号转接固高倒立摆的运动控制板的通信端口，测试所设计滑模控制器的实时控制效果.启动程序时，先将摆杆扶到竖直向上位置附近，即给倒立摆一个接近平衡位置的初始值.数据输出端采集摆杆角度变化和小车运动位置变化，如图5和图6所示.与仿真不同，要将竖直向上的目标位置的摆角设为-3.14 rad.从图5和图6可以看出，小车在目标位置小幅摆动，摆动幅度小于0.03 m，摆杆角度的摆动幅度也小于0.03 rad.仿真数据和试验结果表明了所得控制器的有效性.

图5 摆杆角度实测数据Fig.5 Test result of pendulum angle

图6 小车位置实测数据Fig.6 Test result of pendulum position

4 结语

本设计主要讨论了滑模控制方法在倒立摆稳定控制中的应用.针对倒立摆建模过程中的复杂非线性和系统控制中的不确定干扰因素，提出了滑模控制方法进行控制器设计，并且利用线性矩阵不等式辅助方法完成了反馈控制参数的计算和滑模面的确定.仿真结果和基于固高倒立摆的联机测试结果表明，所设计的控制器能够使倒立摆快速稳定地到达目标位置.

[1] 赵晓军,刘成忠,胡小兵.基于果蝇优化算法的PID控制器设计与应用[J].中南大学学报(自然科学版),2016,47(11):3729-3734.

[2] 王瑶为,邢科新,马剑,等.直线一级倒立摆的自抗扰控制方法及实现[J].控制工程,2017,24(4):711-715.

[3] 王贤明,陈炜,赵新华.倒立摆系统起摆与稳摆控制算法研究综述[J].自动化技术与应用,2015,34(11):5-9.

[4] 孙宁,方勇纯,陈鹤.欠驱动惯性轮摆系统全局滑模控制[J].控制理论与应用,2016,33(5):653-661.

[5] 刘永慧.滑模变结构控制的研究综述[J].上海电机学院学报,2016,19(2):88-93.

[6] 薛鹏，任鹏飞，曹学儒.四旋翼飞行器滑模控制的稳定性分析[J].河南工程学院学报(自然科学版)，2015,27(1)：33-35,43.

[7] 辛腾达,范惠林,闫琳.滑模变结构制导律的抖振问题研究[J].航空兵器,2015(2):10-13.

DesignofslidingmodecontrollerforinvertedpendulumviaLMI

RENPengfei1,ZAHOYushun2，CUIYong1,LIXuejian1

(1.CollegeofElectricalInformationEngineering,HenanUniversityofEngineering,Zhengzhou451191,China;2.HenanShunkangMachineryandElectricEquipmentco.,Ltd.,Zhengzhou450007,China)

Inverted pendulum is a typical under-actuated system. Aiming at the complex nonlinear system, a sliding mode control strategy was proposed with the uncertain disturbance inputs. Sliding mode section was discussed via an linear model. Control design for the certain parts of the system was completed, and the disturbance compensation was also included. To reduce the dependence of parameter debugging on design experience, linear matrix inequality was taken to calculate the feedback gain and slide section parameter. Software simulations and Googol inverted pendulum experiments verified the feasibility of the proposed strategy. The results show that the stability control of the inverted pendulum system can be achieved by using designed controller.

sliding mode control; single chip microcontroller; inverted pendulum; linear matrix inequality

TS111

A

1674-330X(2017)04-0062-04

2017-07-08

河南工程学院大学生创新创业训练计划项目(201611517034)

任鹏飞(1982-)，男，河南郑州人，讲师，主要研究方向为电气工程.