掘进巷道瓦斯爆炸冲击波压力特性研究

杨书召，杜学胜

(河南工程学院 安全工程学院，河南 郑州 451191)

掘进巷道瓦斯爆炸冲击波压力特性研究

杨书召，杜学胜

(河南工程学院 安全工程学院，河南 郑州 451191)

为揭示煤矿掘进头瓦斯爆炸冲击波压力沿复杂巷道衰减变化特性，借助爆炸力学和相似定律理论，建立巷道一维爆炸压力变化计算数学模型和TNT当量系数法试验计算模型.理论和试验模型对比分析表明：掘进头弱瓦斯爆炸的冲击波压力沿稳定断面传播呈非线性变化特性，冲击波压力与传播距离的平方根成反比；冲击波压力遇巷道断面变化或分叉超压大幅度衰减；冲击波压力遇障碍物反射后压力是原来的2倍.瓦斯爆炸超压预测计算模型的计算值、理论计算值与实验值吻合较好，与爆炸冲击波压力的传播特性描述一致.

掘进巷道；瓦斯爆炸；冲击波压力；压力特性

煤矿掘进头瓦斯突然涌出引起的瓦斯爆炸是矿井重大灾害事故的主要原因之一[1].研究表明，这类瓦斯爆炸如果不激起煤尘参与，一般为弱爆炸[2-3].爆炸受巷道环境变化的影响，爆炸超压会造成井下人员伤亡和财产损失.研究瓦斯爆炸压力随巷道变化的特性，有助于煤矿防灾与减灾.

瓦斯爆炸冲击波传播受巷道环境因素制约，超压复杂多变.多年来，国内外学者对此进行了大量研究.苏联学者萨文科[4]通过大量实验，给出了冲击波经巷道拐弯、分叉和变截面等的超压衰减系数；国内学者在大型巷道和管道内对爆炸冲击波超压的变化也做了实验研究[5-6]，并取得了一些实验结果.但在计算如何确定不同时刻冲击波沿复杂巷道的变化量方面，大都停留在实验的基础上且结果各异.

采用理论分析和试验研究相结合的方法，揭示掘进巷道瓦斯爆炸冲击波压力变化特性，以期为防治瓦斯灾害提供理论和技术支持.

1 掘进巷道瓦斯爆炸冲击波压力计算

1.1 一维瓦斯爆炸压力计算模型

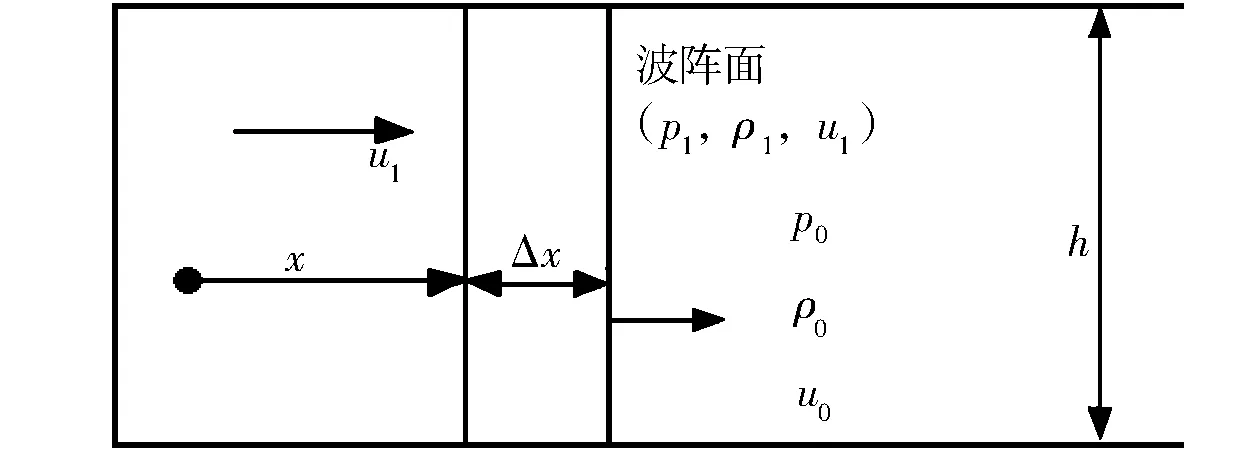
图1 爆炸冲击波一维物理模型Fig.1 One-dimensional physical model of explosion shock wave

掘进巷道瓦斯爆炸物理模型如图1所示.以爆源点为坐标原点，沿波阵面方向为x轴，建立一维坐标系.气体被爆炸产生的冲击波带到了波阵面的附近，厚度为Δx的冲击波内集中了大量的压缩气体，这些气体都在冲击波的作用下被压缩在有限的空间内.因为冲击波的厚度非常小，所以Δx的值也并不大，此薄层内密度等于波后密度ρ1，而且这个薄层内压缩气体的密度也为常数，所以该薄层的厚度为Δx，其质量为m=Sρ1Δx=Sρ0x.图1中，S为巷道截面积，x为冲击波所经过的距离，p0为波前压强，ρ0为空气密度，u0为空气速度.

若厚度为Δx的薄层内气流速度与波阵面后气流速度相等，均为u1，薄层内的压力为p，它是波后压强p1的φ倍，即p=φ·p1.其中,φ值并不确定，波前压强p0与p相比可以忽略.由牛顿第二定律建立薄层内气体微分方程：

(1)

(2)

通过对式(2)积分化简可以得出：

(3)

当不计冲击波与巷道产生的边界摩擦损失及通过热传导、热辐射等其他方式所产生的能量损失等，仅考虑冲击波对波前气体做功所产生的能量损失，则冲击波阵面内气体的动能和内能之和与冲击波对巷道内气体介质所做的功相等.设被薄层气体所包含的气体内能为Er，则

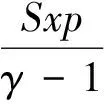
(4)

(5)

当瓦斯的累积量一定时，E为常数.而冲击波对气体介质所做的功与x没有关联，则

(6)

弱爆炸下马赫数Ms接近1，弱冲击波存在如下关系：

(7)

(8)

(9)

由此可得冲击波超压Δp近似计算公式：

(10)

弱爆炸下，空气密度ρ0取1.29 kg/m3，绝热常数γ取1.4，所在地的音速c0取340 m/s.

可以看出，冲击波超压计算模型没有考虑巷道环境变化对冲击波压力的影响.根据苏联学者萨文科实验得出的爆炸冲击波在分岔、变截面和拐弯巷道内的衰减系数θ，β和ξ，见文献[4]，则超压计算公式可写为

(11)

图2 爆炸冲击波反射示意图Fig.2 Schematic diagram of explosion shock wave reflection

1.2 冲击波遇巷道障碍物的压力计算

当爆炸冲击波与障碍物成α角入射，会出现冲击波斜反射.假设0区代表空气未扰动区，l区代表入射波经过而反射波尚未通过区，2区代表反射波经过区，见图2.由入射波阵面的两侧动量和质量守恒，并借助入射波和反射波冲击绝热方程得到反射压力计算模型：

(12)

假设入射波和反射冲击波均是一维定常的，由边界条件和基本关系式可得:

(13)

(14)

式中：下标0表示入射前未扰动压力、密度和速度参数；下标1表示入射后的各参数；下标2表示反射波阵面后的各参数.

若壁面刚性u0=0,u2=0,v0=0,v2=0，可得

(p1-p0)(ρ1ρ2-ρ0ρ2)=(p2-p1)(ρ0ρ2-ρ0ρ1).

(15)

(16)

入射波和反射波的超压为

Δp1=p1-p0，Δp2=p2-p0，

(17)

式中：Δp1，Δp2为入射压力和反射压力.反射波的峰值超压

Δp2=2(p1-p0)+χ(χ-1)(p1-p0)2[(χ+3)(χ-1)p1]-1.

(18)

当空气绝热指数γ=1.4时，

(19)

(20)

2 巷道瓦斯爆炸TNT当量系数法试验计算模型

掘进头巷道瓦斯爆炸可视为一种气云爆炸.采用 TNT当量系数法计算气云爆炸[7-8].瓦斯转化为TNT标准炸药量Q的计算公式：

(21)

式中：Q为当量TNT标准炸药量，kg；爆炸系数ζ=0.6；TNT炸药转化率n=0.2；瓦斯密度ρ=0.716 kg/m3(标准状态下)；VCH4为瓦斯体积，m3；TNT炸药的发热量QT=4 186.8 kJ/kg，即1 m3瓦斯(标准状态下)参与爆炸时的爆炸能量与0.945 kg TNT炸药相当.

根据相似定律，采用如下有量纲比例参数：

(22)

式中：Z为有量纲比例距离；x为掘进头巷道中瓦斯爆炸超压测点距爆源中心的距离；Q为独头巷道瓦斯爆炸实验中瓦斯TNT当量.

在煤炭科学研究总院重庆研究院全尺寸实验巷道进行了纯瓦斯爆炸实验[9-10]，实验方案内容详见文献[2].为了与实验进行对比，在瓦斯体积分数为9.5%、长886 m、断面面积为7.2 m2的独头巷道矿井中进行50 m3，100 m3和200 m3爆炸实验所得超压，利用最小二乘法将其展开为多项式并进行回归处理得到

(23)

考虑瓦斯体积对爆炸的影响，用矿井独头巷道100 m3瓦斯爆炸时各测点爆炸实验中测得的超压拟合同等浓度、不同体积的瓦斯-空气混合气体的爆炸超压计算模型：

(24)

式中：V为空气和瓦斯混合气体的体积，m3.

3 瓦斯爆炸冲击波压力模型分析

图3与图4为 50 m3和200 m3的瓦斯爆炸超压理论值、拟合预测值和实验值，实验数据依据文献[3]和文献[9].

图3 50 m3的瓦斯爆炸超压理论值、预测值和实验值Fig.3 Theoretical values, predicted values and experimental values of gas explosion over 50 m3

图4 200 m3的瓦斯爆炸超压理论值、预测值和实验值Fig.4 Theoretical values, predicted values and experimental values of gas explosion over 200 m3

从图3和图4可以看出，由瓦斯爆炸拟合得到的压力计算模型能满足对50 m3，100 m3，200 m3爆炸源瓦斯混合气体爆炸冲击压力的预测，实验值、理论值和拟合预测值基本符合.

4 结论

(1)掘进头瓦斯爆炸在沿巷道传播时，爆炸一般为弱爆炸，其冲击波压力衰减受巷道环境影响较大，巷道断面不变时，爆炸压力传播呈非线性变化.

(2)掘进巷道内的爆炸冲击波压力随传播距离增加而衰减，遇巷道截面变化、分岔和拐弯等均快速衰减，遇巷道障碍物冲击波出现叠加，反射压力加倍.

(3)瓦斯爆炸沿掘进巷道传播的冲击波超压的理论计算模型和TNT当量系数法拟合的预测计算模型，理论值与实验值基本吻合，满足爆炸计算误差，为煤矿瓦斯爆炸事故调查、勘验和分析等提供了两种计算方法.

[1] 林柏泉．矿井瓦斯防治理论与技术[M]．2版.徐州：中国矿业大学出版社，2010.

[2] 曲志明，周心权，王海燕，等．瓦斯爆炸冲击波超压的衰减规律[J]．煤炭学报，2008，10(4):410-414．

[3] 王海燕,曹涛,周心权，等. 煤矿瓦斯爆炸冲击波衰减规律研究与应用[J].煤炭学报,2009，34(6)：771-782.

[4] 萨文科.井下空气冲击波[M]．龙维祺，译.北京：冶金工业出版社，1979:100-114.

[5] 林柏泉，周世宁.障碍物对瓦斯爆炸过程中火焰和爆炸波的影响[J]．中国矿业大学学报，1999，8(2)：104-107.

[6] 张连玉，汪令羽，吴维．爆炸气体动力学基础[M]．北京：北京工业学院出版社，1987：370-374．

[7] 费国云．瓦斯爆炸沿巷道传播特性探讨[J].煤矿安全，l996，27(2)：32-34.

[8] 徐景德,徐胜利,杨庚宇,等.矿井瓦斯爆炸传播的实验研究[J].科学技术,2004,3(7):55-57.

[9] 吴兵.矿井半剑闭空间瓦斯爆燃过程热动力学研究[D]．北京：中国矿业大学(北京),2003.

[10]杨书召，吴金刚.半封闭空间瓦斯爆炸冲击波传播距离研究[J].湖南科技大学学报(自然科学版)，2014，29(1)：8-11.

Studyonpressurecharacteristicsofgasexplosionshockwaveindrivingtunnel

YANGShuzhao，DUXuesheng

(CollegeofSafetyEngineering，HenanUniversityofEngineering，Zhengzhou451191,China)

In order to reveal the characteristics of the attenuation of the shock wave along the complex roadway, with the mechanics of explosion and similitude theory, mathematic model and equivalent coefficient TNT test explosion pressure calculation model of one-dimensional tunnel was established. Theoretical analysis and model test results show that the weak head pressure of blast wave propagation along the stability section is nonlinear characteristics, the impact of the square root size and the pressure wave propagation is inversely proportional to the distance. The pressure of the shock wave decreases greatly when the cross section changes or the bifurcation of the roadway. The calculated value and theoretical calculation value of the prediction model of the overpressure of gas explosion coincide well with the experimental values, and the propagation characteristics of the explosion shock pressure are consistent with those of the three.

driving roadway; gas explosion; shock wave pressure; pressure characteristics

TD712

A

1674-330X(2017)04-0035-04

2017-08-13

河南工程学院博士基金(062701/D2013019)

杨书召(1969-)，男，河南内乡人，教授，博士，主要从事瓦斯防治方面的研究.