几道2017年数学竞赛不等式加强及推广

江苏省苏州市工业园区新馨花园17幢409室 (215000)

陈罗英

几道2017年数学竞赛不等式加强及推广

江苏省苏州市工业园区新馨花园17幢409室 (215000)

陈罗英

2017年各国数学竞赛题中，运用初等方法证明不等式，仍然是一个主要方面.笔者发现，有些不等式试题可以加强及推广.

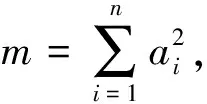
当n=3,λ=1时，依次取a1=a,a2=b,a3=c，即为原赛题.

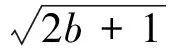
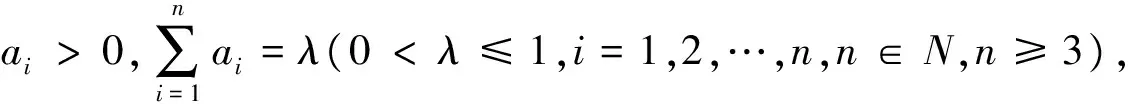
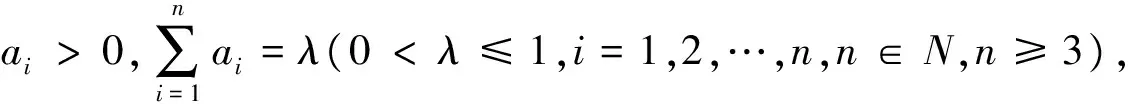
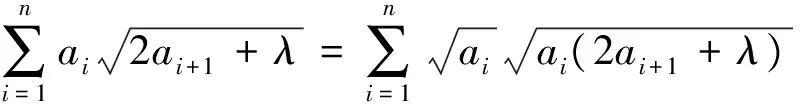
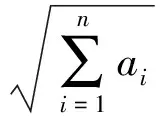
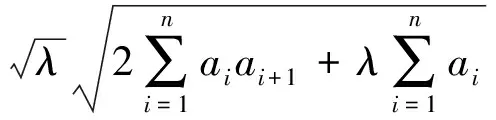
由此可见，原赛题存在下界.

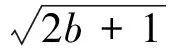
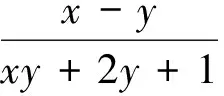
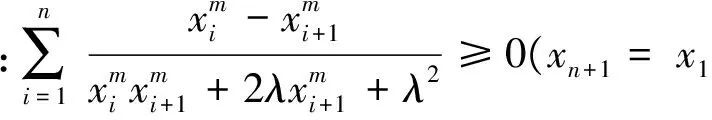
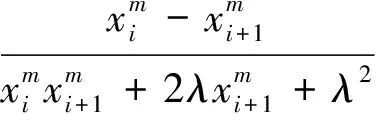
当n=3,m=1,λ=1时，依次令x1=x,x2=y,x3=z，即为原赛题.

例4[3](2016年阿塞拜疆数学奥林匹克试题)

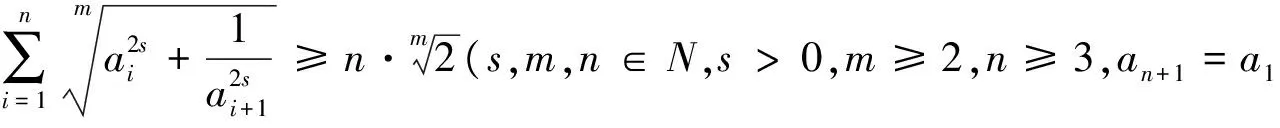
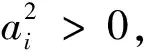
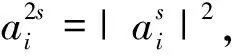
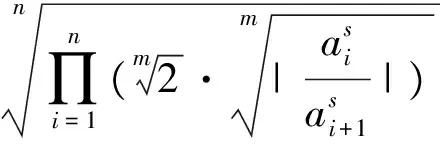
当n=3,m=2,s=1时，依次令a=a1,b=a2,c=a3时，即为原赛题.

[1]陈少春.2017年数学竞赛不等式赏析[J].中学数学研究(江西),2017,8.

[2]blog.sina.com.cn/s/blog_494a3afd0102v...-快照-新浪博客.

[3]吴盛盛,李加军.四道2016年数学奥林匹克试题的多种证法[J].中学数学研究(江西),2017,8.