“弹塑性力学”结构体系及教学方法探讨

2018-01-03刘红岩吕建国

中国地质教育 2017年4期

关键词：弹塑性本构屈服

刘红岩，吕建国

中国地质大学（北京）工程技术学院，北京 100083

“弹塑性力学”结构体系及教学方法探讨

刘红岩，吕建国

中国地质大学（北京）工程技术学院，北京 100083

“弹塑性力学”是中国地质大学（北京）工程类硕士研究生的一门专业基础必修课，具有高度的抽象性、理论性强及知识点多等特点，因而出现了教师难教和学生难学的现象。为此笔者基于多年的课堂教学实践，从本课程的教学大纲及教学内容出发，首先对课程总体结构体系及各章节之间的逻辑联系进行了详细分析，其次对教材中的几个难点问题进行了详细的探讨，最后在此基础上提出了总体—局部—总体的教学方法。

弹塑性力学；结构体系；教学方法

“弹塑性力学”是中国地质大学（北京）工程技术学院工科专业硕士学位研究生的核心基础课程之一，根据我院工科专业的研究生培养目标[1]，即：掌握坚实的数学、力学理论和系统的专业知识，熟悉本学科的国内外研究现状及发展趋势，我们制定了该课程的教学大纲，并选择了由徐秉业和刘信声共同编写的《应用弹塑性力学》作为主讲教材[2]。众所周知，力学课程一般比较抽象、难懂，它不但需要很多前期的数学及力学课程为基础，而且还需要开展相应的物理试验以积累感性认识，然而由于课时的限制，一些前期课程如张量分析和物理试验等都难以开展，因而更容易导致学生“课堂上听不懂，课下不会做作业”的普遍性问题。为此，针对该课程教学中存在的问题，不少教师分别从不同角度对其教学方法进行了较为详细和深入的研究与探讨。如林高用等从教学内容和教学方法上进行改革，采用工程案例的教学模式，使得教学效果明显提高[3]；徐鹏从教学内容、教学方法和考核评价等方面进行教学总体设计和实践，以工程应用为目的探讨了全日制专业学位研究生力学课程的教学方法[4]；杜冰等基于国外的工程教育教学理念，并结合多年教学经验，从理论教学、实践教学、考核机制及现代设计与教学工具等多个方面对该课程的教学方法进行了探讨[5]；原方等从启发式与讨论式教学的角度对该课程的教学改革进行了探索[6]。上述研究极大地促进了“弹塑性力学”课程教学方法的改革，取得了很好的教学效果。但是上述研究主要是针对某一具体内容或方法进行研究的，而对该课程总体上的把握略显不足，因此也导致学生对该课程的系统性及章节之间的联系把握不够。为此本文拟借鉴刘红岩等的研究方法，从系统论的角度出发，首先对该课程的内容进行整体上的概括，分析各章节之间的有机联系及层次结构，让学生对本课程有一个整体框架上的认识，然后再针对课程中具体的难点和重点问题进行逐个分析讲解，最终使学生能够很好地掌握本课程的主要内容[7]。

一、课程内容的结构体系分析

尽管“弹塑性力学”的教学大纲是由教育部统一制定的，但是不同高等院校间选用的“弹塑性力学”教材却不尽相同，这里就以我院采用的《应用弹塑性力学》教材为例进行说明。

根据人类认识事物的一般规律：总体—局部—总体，因此应从总体上让学生了解“弹塑性力学”在研究生学习阶段中的基础地位及作用；其次，就是介绍其研究对象、研究内容及方法；最后，对其在实际工程问题中的应用进行探讨和研究。

按照上述思路，首先，我们对教材内容结构体系进行分析（图1）。在研究角度上，其研究对象为线弹性体和理想弹塑性体；在研究内容上，它主要研究应力分析、应变分析、弹塑性的应力应变分析、弹塑性力学的解题方法和典型的弹塑性力学问题等；在研究手段上，该课程主要是采用理论方法和试验方法，如在应力分析和应变分析中主要是采用理论方法，而在塑性材料的屈服准则及塑性本构关系的建立方面，则更多是在根据试验结果进行假设的基础上，结合相应的理论方法最终获得相应的研究结论。

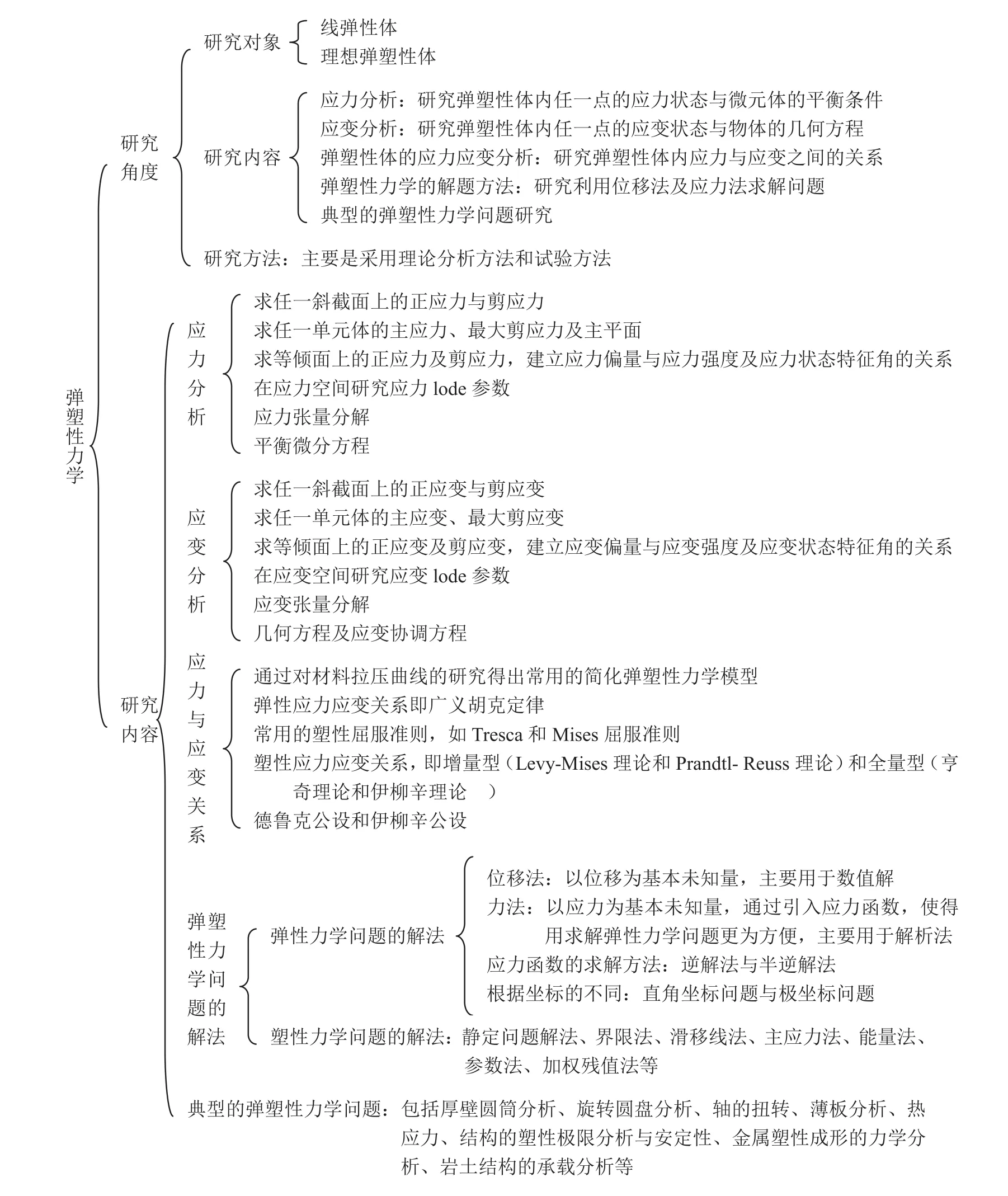
图1 “弹塑性力学”结构体系图

其次，在研究内容上，关于应力分析主要是采用理论推导的方法研究了三维空间内任一斜截面上的应力计算方法；任意单元体上的主应力、最大剪应力及主平面的计算方法；等倾面的引入及等倾面上的正应力和剪应力计算方法、应力偏量与应力强度及应力状态特征角的关系，这为后面的剪切屈服准则及理想塑性本构关系的建立奠定了基础；应力lode参数的引入、应力张量的分解及平衡微分方程的建立等等。关于应变分析的研究与之类似，同样也是研究了任一斜截面上的正应变与剪应变；任意单元体上的主应变和最大剪应变的计算方法；等倾面上正应变及剪应变的求法，应变偏量与应变强度及应变状态特征角的函数关系，这同样也为塑性本构关系的建立奠定了基础；应变lode参数的引入、应变张量的分解及几何方程和应变协调方程的建立等等。关于应力应变关系，主要介绍了弹性胡克定律、材料塑性屈服准则（Tresca屈服准则和Mises屈服准则）、两类塑性本构关系（增量型本构关系和全量型本构关系）及两个基本公设（德鲁克公设和伊柳辛公设）。第四章弹塑性力学问题的求解方法和第五～十二章典型的弹塑性力学问题则是上述理论在弹塑性问题求解中的应用。

上述内容即是对“弹塑性力学”课程内容的归纳总结，学生由图1可以很容易地从总体上把握本课程的全部内容及各章节之间的关系，进而理清其逻辑结构，达到学习和掌握的目的。

二、课程中的关键内容及其教学方法研究

在“弹塑性力学”中有几个内容是理解和掌握本课程的关键，同时也是比较抽象、难懂的问题，因此在教学过程中应给予足够的重视，应通过反复、多角度地讲解从而让学生能够彻底明白其中的道理，这样才能达到事半功倍的效果。下面笔者就根据我们自己的理解及教学过程中学生的反馈对本课程中的几个关键问题进行探讨。

1.等倾面提出的意义及其教学方法

通过本课程的学习，我们知道等倾面在“弹塑性力学”的研究中贯穿始终，对弹塑性理论的建立具有重要作用。但是学生对等倾面的理解和接受却没有那么容易。首先从定义上来看，等倾面就是一个与三个主应力轴成相同角度的面，进而等倾面上的应力可以分解为垂直于等倾面的正应力和在等倾面内的切应力。而垂直于等倾面的正应力为三个主应力的平均值，该应力即为静水压力，它不会引起材料屈服，进而得出材料的屈服面应该是以π平面（过坐标原点的等倾面）的法线为中心轴线的柱面，由此可得出材料的屈服面具有外凸特性。其次，把由三个主应力组成的应力空间向等倾面上投影，那么就可以得到三个互成120°的坐标轴。该方法的巧妙之处在于经过投影以后，等倾面上的正应力在投影后的坐标系上为零，由于我们已经通过试验知道静水压力不会引起材料屈服，这样就可以在投影后的坐标系上仅考虑切应力对材料屈服的影响。第三，可以用来研究理想塑性材料的增量型本构关系，即通过对投影后各应力矢量和的分析可以得到应力偏量与应力强度及应力形式指数之间的函数关系。同样在以主应变为坐标轴的应变空间中，将其投影到等倾面上也可以得到三个互成120°的坐标轴，进而根据相应的几何关系可以得到应变偏量与应变强度及应变形式指数间的函数关系。

同时Lode通过对受轴向拉伸与内压共同作用的薄壁圆管作试验，发现应力Lode参数与塑性应变增量Lode参数相等，再考虑Lode参数与应力形式指数之间的关系，进而可以得到应力形式指数与塑性应变增量形式指数相等，最终在不考虑体积变形的条件下，可得到著名的Levy-Mises增量型本构方程；进而由该方法可以得到其他几种著名的塑性本构方程，如增量型的Prandtl-Reuss方程和全量型的亨奇和伊柳辛方程。因此可以看出，等倾面在研究材料弹塑性本构关系方面具有重要作用。

关于等倾面的知识在本教材前三章都有介绍和应用，因此在教学过程中应注重各自然章节之间的联系，实现知识点的纵向贯穿，抓住等倾面这一主线就可以让学生很顺利地了解和掌握增量型及全量型的理想弹塑性本构方程的建立过程。

2.Lode参数提出的意义及其教学方法

由于应力Lode参数与应变Lode参数类似，因此下面以前者为例讨论其物理意义。应力Lode参数μσ是弹塑性力学中一个十分重要的参数，它可以描述物体内一点的应力状态类型及特征[8]。在弹塑性力学中引入μσ有三个重要意义，一是考虑了中间主应力σ2对材料屈服的影响，在弹塑性力学中有两个常用的屈服准则，即Tresca和Mises屈服准则，当中间主应力σ2在最大主应力σ1和最小主应力σ3之间变化时，相应地μσ则在[1,-1]之间变化，即中间主应力σ2对材料的屈服强度将有较大影响，因此可以认为应力Lode参数μσ很好地反映了中间主应力对材料屈服的影响。二是根据塑性力学假设，认为静水压力不会引起材料屈服，而应力Lode参数μσ也可以表示为偏应力之差，这说明μσ也能很好地反映这一规律。三是如前所述Lode参数在塑性本构关系的建立中也具有非常重要的作用，这里就不再重述。

由此可知，Lode参数在弹塑性力学理论中占有非常重要的地位，在教学中应向学生充分阐述其重要性，通过介绍其提出背景、定义及应用等几个方面对其进行全面阐述、加深学生的理解，认识到其重要性，而不是让学生仅仅认为只是多提出了一个力学参数而已。

3.引入德鲁克公设和伊柳辛公设的意义及其教学方法

这里以德鲁克公设为例进行介绍，德鲁克公设是经典塑性力学的重要基础，也是现代塑性理论发展的基石，由它不仅可以直接导出关联流动法则以及塑性应变增量与屈服面的正交性，而且还可以建立塑性状态下的本构方程[9]。因此，德鲁克公设把材料的屈服条件与塑性本构方程联系起来了，同时该公设的提出使得经典塑性理论有了比较严密的数学理论体系。

根据德鲁克公设，塑性应变增量与屈服面正交，若令塑性势函数等于屈服函数，则可得到关联流动法则。若取其屈服条件为Mises屈服条件，且不考虑塑性阶段的体积变形，即为Levy-Mises增量型本构方程。

因此德鲁克公设与理想材料的塑性本构关系之间是相互印证、相互促进的，而不是互相独立、彼此无关的。总之，德鲁克公设和伊柳辛公设的提出为塑性力学的发展起到了重要推导作用。因此在教学中应向学生深入介绍这两个公设与材料塑性本构关系之间的联系，从而在加深学生对其理解的同时认识到其在整个塑性理论体系中的作用和地位。

三、结语

笔者针对“弹塑性力学”教学中学生反映的课程难懂难学的问题，结合自己在教学过程中的体会，提出了从总体—局部—总体的教学方法，即首先采用结构体系分析方法对课程内容及章节之间的逻辑关系进行了分析、归纳和总结，然后针对教学过程中学生感到难以理解的几个问题进行了专门解答。这种基于课程结构体系的教学方法使学生能够在听课过程中做到思路清晰、层次鲜明，避免了因概念多、公式多而导致的思路不清、摸不着方向的感觉。经过实践，这种教学方法取得了初步的良好效果。同时，以结构体系图的方式表达课程各章节及知识点之间的逻辑关联，也能很好地培养和锻炼学生的逻辑思维与综合分析问题的能力，从而达到培养学生自我学习和自我解决问题的能力。

[1]吕建国，王贵和．地质工程专业研究生力学课程的改革与思考[J]．高等理科教育，2003，（S2）：130-131．

[2]徐秉业，刘信声．应用弹塑性力学[M]．北京：清华大学出版社，1995．

[3]林高用，杨立斌，陈明安，等．《弹塑性力学》课程教学的改革与实践[J]．湖南医科大学学报（社会科学版），2006，8（1）：205-207．

[4]徐鹏．全日制专业学位研究生力学课程教学设计与实践[J]．中国电力教育，2013（35）：92-93．

[5]杜冰，王超．新型教学理念及其在“弹塑性力学基础”教学上的实践[J]．教育教学论坛，2016（32）：137-138．

[6]原方，吴洁．研究生弹性力学教学方法及问题探讨[J]．力学与实践，2005，27（2）：82-84．

[7]刘红岩，李冬梅，罗志华，等．“理论力学”课程内容的逻辑关联分析及教学方法研究[J]．中国地质教育，2010，19（1）：82-85．

[8]刘家信．关于塑性力学中的Lode参数[J]．东北重型机械学院学报，1987，11（1）：70-78．

[9]曲圣年，殷有泉．塑性力学的Drucker公设和Ильюшин公设[J]．力学学报，1981（5）：465-473．

elasticity and plasticity Mechanics; structure system; teaching method

G642

1006-9372（2017）04-0032-04