并联机器人位姿正解优化算法及其仿真

李穆远 全惠敏 吴桂清

(湖南大学电气与信息工程学院 湖南 长沙 410082)

并联机器人位姿正解优化算法及其仿真

李穆远 全惠敏*吴桂清

(湖南大学电气与信息工程学院 湖南 长沙 410082)

选取3-6结构并联机器人为研究模型，根据构型间的约束关系，建立机构的位姿正解的求解模型，并采用改进粒子群算法进行求解，将复杂的位姿正解问题转化为多元非线性方程的寻优过程。为提高求解精度，利用混沌序列的不可预测性与无序性以及在一定范围内不重复遍历所有状态的特性，提出一种基于混沌序列调整惯性权重的改进粒子群算法，将其用于求解位姿正解的计算。计算实例表明，该算法能求解出全部的位姿正解，且相较于标准粒子群算法能达到更高的收敛精度。最后采用SolidWorks和Adams进行联合仿真，验证了这种优化算法的可行性。

位姿正解 粒子群算法 混沌序列 惯性权重 Adams仿真

0 引 言

并联机器人相对于串联机器人具有较高的精度、很强的承载能力及较快的响应速度等优点，故现在已被广泛地应用到各个领域[1]。目前较新的应用领域有：应用于虚拟现实的4D或5D影院运动座椅，应用于互动游戏的模拟运动平台等。给定并联机器人的杆长变量求解机器人运动平台位姿，称为并联机器人的位置正解，并联机构位姿正解是并联机构运动学分析的基础[2]。在这一求解过程中，由于构型的复杂性和耦合性，采用一般的数值计算方法很难求解，所以正解问题已成为并联机器人机构运动分析的难点和重点之一，国内外许多学者对其进行了大量的研究，并提出了多种解法[3-7]。常见解法有代数法和数值法[8-9]。传统的数值法主要是通过Newton 法或Newton-Raphson 法迭代求解[10-11]。粒子群算法由于其搜索速度快、效率高，算法简单等优点，已经广泛应用在并联机器人的正解问题的求解之中。刘伟锐等提出采用一种改进的粒子群算法求解并联机构的位姿正解[12]，耿明超等提出采用一种基于拟newton法求解位姿正解的方法[13]。本文提出改进的粒子群算法——混沌序列调整惯性权重的粒子群算法，并将其用于求解3-6结构并联机器人平台的位置正解解算之中。

1 并联机器人位姿正解的数学模型

图1所示为3-6结构并联机器人平台的结构简图。

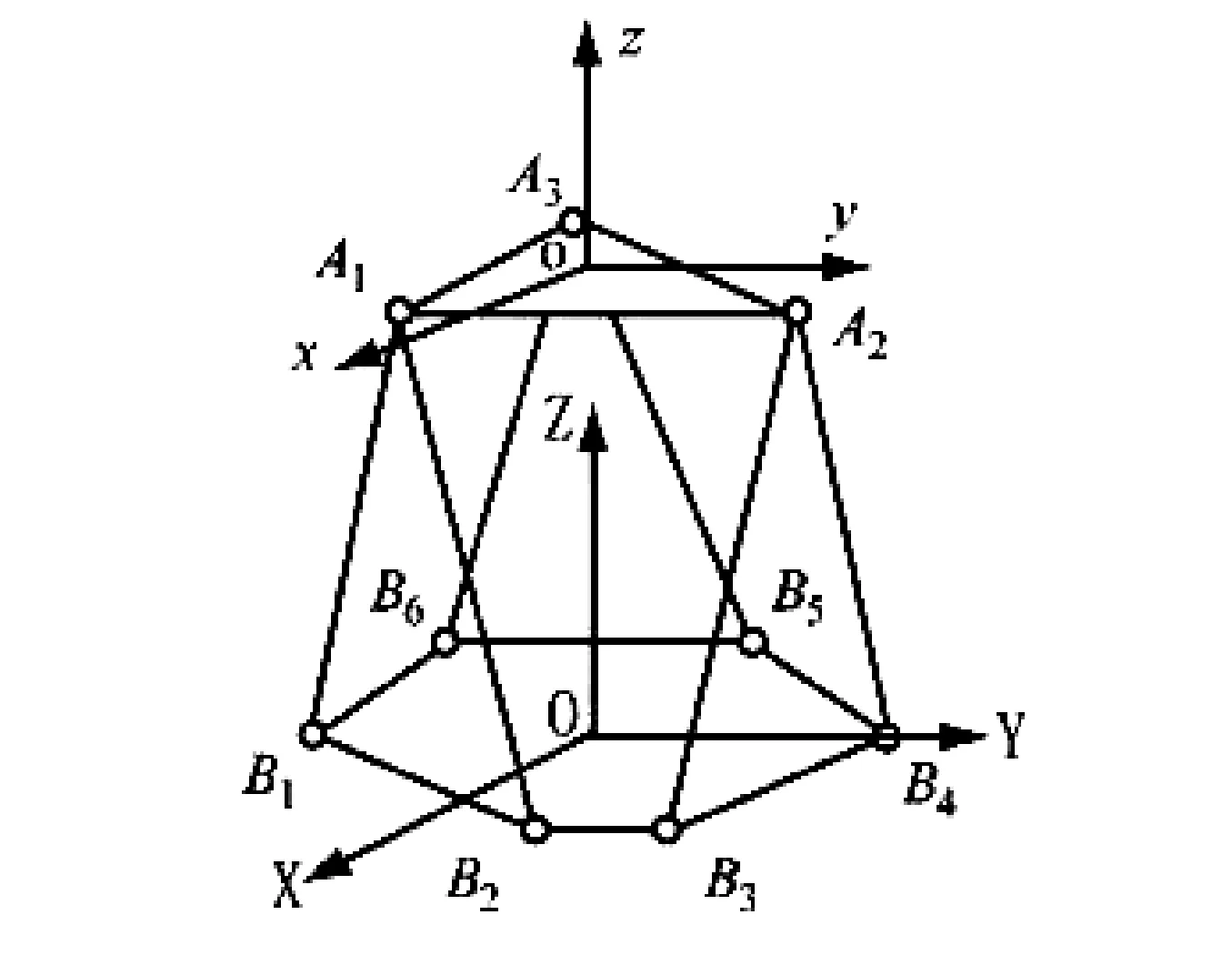
图1 3-6结构并联机器人结构简图

如图1所示该机构由上面运动平台，下面固定平台和6台可伸缩的电缸构成，上下平台和电缸之间采用铰链来连接，上下平台分别为一个正三角形和一个正六边形。在定平台上建立定坐标系O-XYZ，原点O位于定平台的几何中心，Y轴与B1B4重合，Z轴与定平台垂直，X轴遵守右手坐标系规则。O-XYZ为动坐标系，原点O位于动平台的中心点，Y轴与A1A2平行，Z轴与动平台垂直，X轴同样遵守右手坐标系规则。上平台边长为a，下平台边长为b，第i台电缸的长度为Li(i=1,2,…,6)。上平台三个顶点在动坐标系中的坐标矢量为：

下面正六边形的六个顶点在O-XYZ中的坐标矢量为：

设上平台的几何中心点O在定坐标系中的坐标矢量为OA=[XA,YA,ZA]T,用Z-Y-X型Euler角(α,β,γ)表示动平台的姿态，则动坐标系相对于定坐标系的方向余弦矩阵可表示为：

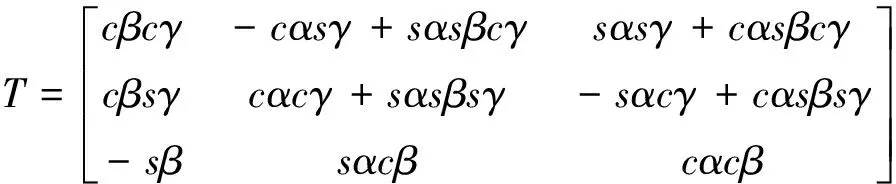
式中：“s”表示“sin”,“c”表示“cos”。则点Ai(i=1,2,3)的坐标可以通过如下变换公式转换成定坐标系中的坐标矢量：

AOi=TAi+oAi=1,2,3

(1)

根据电缸的约束条件得：

‖AO1-Bi‖=Lii=1,2‖AO2-Bi‖=Lii=3,4‖AO3-Bi‖=Lii=5,6

(2)

令x=[x1,x2,x3,x4,x5,x6]T=[α,β,γ,XA,YA,ZA]T，则式(2)转换为非线性方程组：

F(x)=[f1(x),f2(x),…,f6(x)]T=0

(3)

其中：

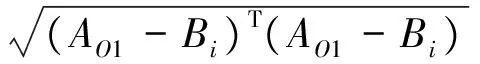
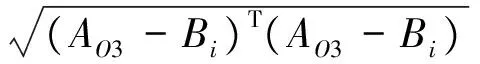
根据并联机构的约束关系，方程组fi(x)取值为零是最理想的状态，此时对应的方程解代表最精确的正解位姿，所以将方程组fi(x)转换为求解最小值的无约束优化模型：

(4)

根据无约束优化模型，可以求出用来描述上平台位姿的六个最优参数P=[α,β,γ,XA,YA,ZA]。即在给定电缸的伸长度时，可用上述模型求解出平台的位姿参数。由于上下平台坐标信息是根据不同的坐标系确定的，以及平台尺寸的标示单位可能不同，在进行计算之前先要进行参数的无量纲化。

2 并联机构位置正解的改进粒子群算法

2.1 标准粒子群算法(PSO)

标准粒子群算法采用文献[14]中的表述，假设搜索空间是n维的，粒子群中第i个粒子的位置用xi(xi1,xi2,…,xin)表示，第i个粒子的速度用vi=(vi1,vi2,…,vin)表示，第i个粒子的个体最好位置为pi=(pi1,pi2,…,pin)，整个粒子群目前搜索到的最好位置为pg=(pg1,pg2,…,pgn)，下一代粒子的第d(1≤d≤n)维的速度和位置根据下面的方程来更新：

(5)

(6)

式中：c1和c2是学习因子，是两个非负常数，r1和r2是介于[0,1]之间的随机数，为了使粒子在有效的区域内搜索，通常将粒子速度限定在[-vmax,vmax]之间，vmax是由用户设定的常数，ω为惯性权重。惯性权重较大有利于提高算法的全局搜索能力，而惯性权重较小会增强算法的局部搜索能力，因此其值的选取直接关系算法的开发能力和探索能力[15]。为提高算法的收敛性能，避免早熟问题和陷入局部最优问题，许多学者对标准粒子群算法进行各种改进。姜长元等提出一种正弦调整惯性权重的方法[16]。许少华等通过自适应的惯性权重来改进粒子群算法[17]。

2.2 基于混沌序列调整权重的粒子群算法

混沌运动具有无序性、不可预测性、对初值的敏感性，能按其自身的“规律”在一定范围内不重复遍历所有状态，Coelho等将混沌序列应用到不同进化过程的变异操作，以增强算法的寻优能力[18]。

由于混沌序列具有较好的遍历性和随机性的特性，且可以不重复遍历所有的状态，故可以通过一维混沌自映射产生混沌序列来调整粒子惯性权重，方程表述如公式：

ω(t)=f(ω(t-1))

(7)

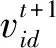
(8)

其中：ω(t)是第t次迭代的惯性权重，粒子的速度按式(8)进行更新。由式(7)生成的惯性权重，将具有混沌特性。最常用的混沌映射就是Logistic映射[19]：

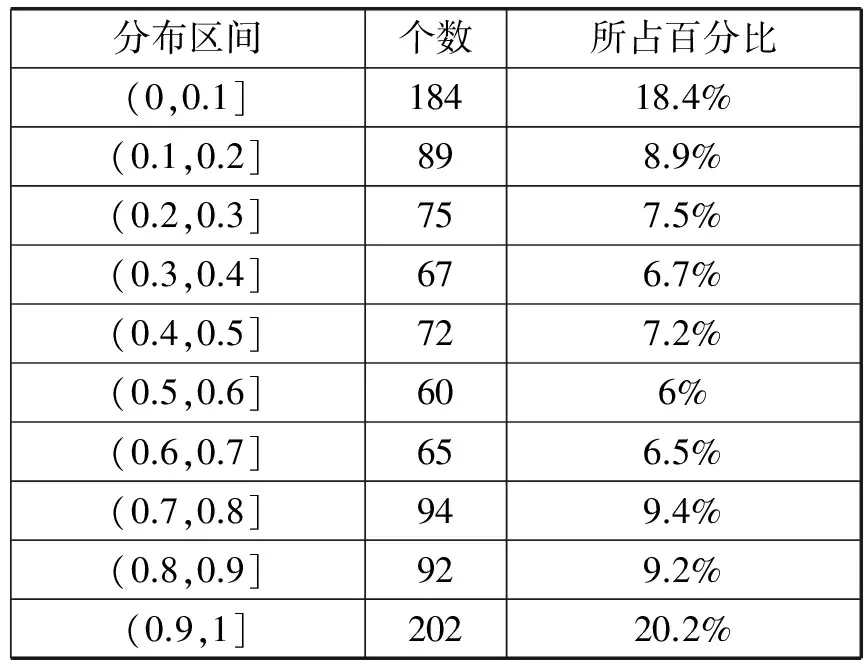
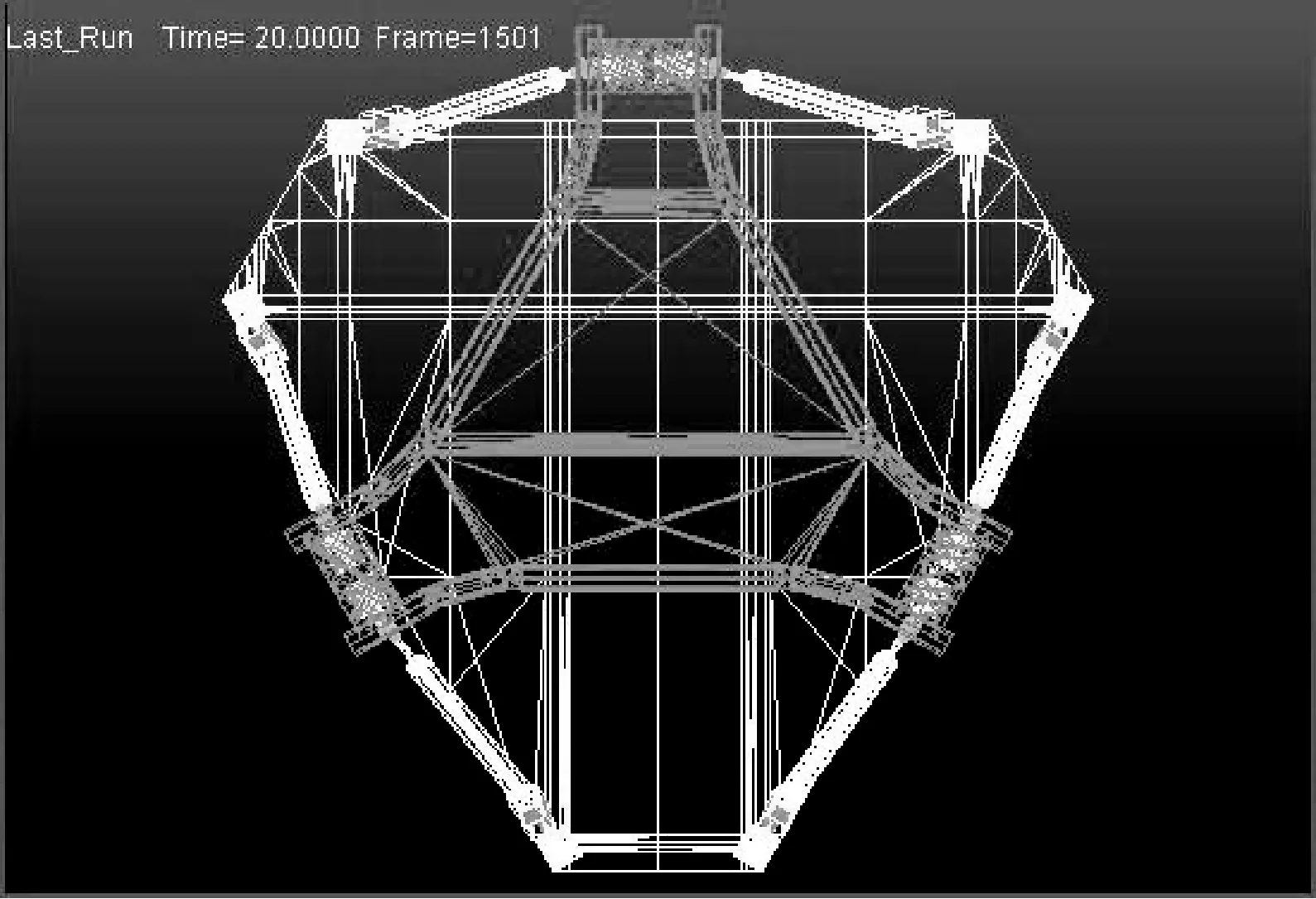
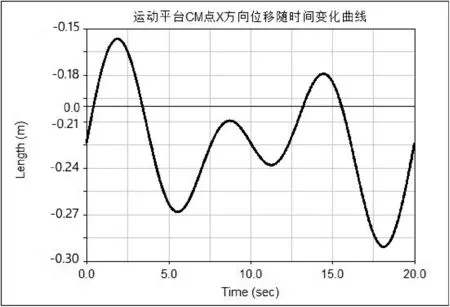
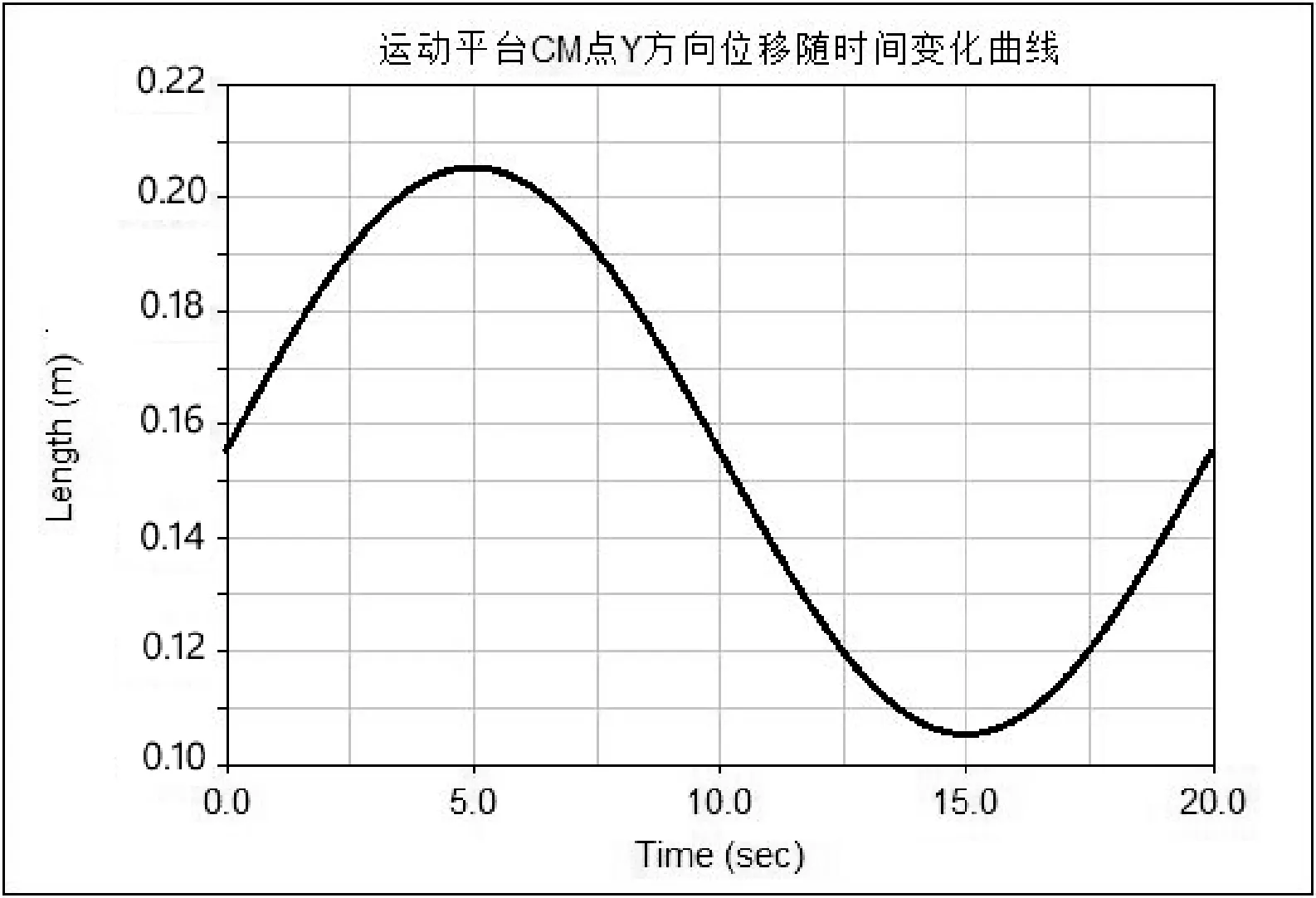
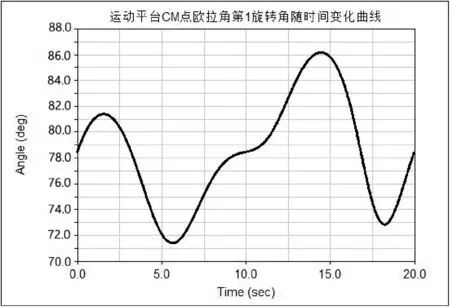
Zg+1=μZg(1-Zg) 0

(9)

其中：μ是控制参量，随着μ的改变会呈现复杂多变的状态，μ的取值决定着惯性权重Z的变化规律。取μ=0.4，由于混沌序列对初值的敏感性，为保证算法收敛，根据文献[6]中得出的经验值，取初值Z0=0.54，式(9)处于完全混沌状态。式(7)中t为1 000次时惯性权重L1的分布情况如图2所示，由该图可知，Logistic映射所产生的惯性权重遍历性较好,且产生的权重分布在经验值[0，1]的范围之中,故相较于一般的线性减少策略能更好地调整搜索空间。

图2 Logistic映射生成的惯性权重

为了进一步分析混沌权重分布的特性，对Logistic混沌映射进行了1 000次的迭代后对其值进行统计，分布情况如表1所示。我们发现得到的混沌惯性权重在两头分布的概率较大，这满足我们希望惯性权重在“某一时期”较大或较小的要求，而在其他区间则相对均匀，这有利于全局搜索的遍历性。

表1 混沌权重迭代1 000次分布情况统计

3 3-6结构并联机器人正解实例计算

将3-6结构并联机器人的边长量及电缸的变化量相对于动平台边长无量纲化，得到本次实例计算的无量纲参数如表2所示。

表2 边长量及电缸的变化量

将待求参数P=[α,β,γ,XA,YA,ZA]看作为粒子位置，将式(5)视为粒子群的适应度函数，采用第2节给出的基于混沌惯性权重的粒子群算法求解该机构的位姿正解。

仿真实验中，取最大测试次数为50次，c1和c2取为2，种群个数n=50，迭代次数取为1 000，维数取为6。采用Visual Studio 2013编程求解。运行结果显示：适应度函数最优值为0，最差值为1.380 507E-30，最优平均值为2.051 038E-31，图3所示为适应度函数的收敛曲线。由于优化算法是在标准粒子群算法基础上进行改进的，为了证明算法的优化性，对改进算法和标准粒子群算法进行收敛精度与迭代速度上的比较。从图中不难发现，改进后的粒子群算法能达到的收敛精度明显高于标准粒子群算法，且收敛曲线的下降速度快于标准粒子群算法，从仿真结果来看，这种改进算法具有更加良好的优化效果，说明在标准粒子群算法基础上采用混沌序列来调整惯性权重这种优化方法是行之有效的。表3所示为采用基于混沌惯性权重的粒子群算法求解的一组对应于本次计算给定边长量及电缸的变化量的全部运动学正解。

图3 适应度函数的收敛曲线

序号α(°)β(°)γ(°)XAYAZA179．67547．46810．0640-0．2820．1301．571279．78750．3087．7630-0．3180．1111．561380．29148．62512．2600-0．2990．1421．566481．06344．8618．1520-0．2730．1801．562584．68245．78914．2520-0．2620．1601．575679．07944．77311．9680-0．2460．1461．579781．45844．9278．7450-0．23470．1241．573878．14343．8362．9010-0．2440．1431．560977．52141．1164．8860-0．2080．1591．5691080．60642．23610．5150-0．1980．1391．5821181．88247．7606．6130-0．2710．1061．5631273．10047．5103．9540-0．2740．1511．5971378．66446．1918．4010-0．2560．1831．6001475．11844．8922．4540-0．2660．2031．5871585．29148．62512．2600-0．2990．1421．5661682．69445．81017．6010-0．2730．1831．5771781．06344．8618．1520-0．2730．1801．5621879．07944．77311．9680-0．2460．1461．5791981．45844．9278．7450-0．2350．1241．573

续表3

4 SolidWorks和Adams联合仿真分析

本文采用SolidWorks构建并联机器人模拟平台，然后将模型导入Adams仿真软件中进行位姿仿真，模型白色条状部分为下平台，黑色条状部分为运动平台，如图4所示。

图4 运动平台模型结构图

本次联合仿真试验选取运动平台的中心点为测量对象，在Adams模型中中心点被标记为CM点，本次仿真分析CM点在给定的驱动下，XYZ方向上的位移和时间的关系，以及欧拉角三个旋转角度随时间的变化关系，以此来验证算法的可行性。

在Adams仿真试验中采用的驱动方程为：

TraX=0.25sin(0.2πt)TraY=0.25sin(0.3πt)TraZ=0.25sin(0.1πt)

(10)

本次仿真时间设置为20 s,CM点在XYZ方向上速度变化随时间的关系如图5所示。

图5 CM点XYZ方向上的速度随时间变化曲线图

最后得到CM点的位移、角度随时间变化曲线如图6-图8所示。

图6 CM点在X方向上随时间变化曲线图

图7 CM点在Y方向上随时间变化曲线图

图8 CM点在Z方向上随时间变化曲线图

CM点欧拉角三个旋转角度随时间变化情况如图9-图11所示。

图9 CM点欧拉角第1旋转角随时间变化曲线图

图10 CM点欧拉角第2旋转角随时间变化曲线图

图11 CM点欧拉角第3旋转角随时间变化曲线图

由仿真曲线可以看到，运动平台的CM点在XYZ方向上的位移范围分别为：[-0.30，-0.15]，[0.10,0.22]，[1.52,1.66],CM点欧拉角的三个旋转角度的变化范围分别为：[70.0°,80.0°]，[40.0°,52.0°]，[2.0°,20.0°]。在第3节中实例计算得到的最优解的结果全落在CM点的位移和旋转角度变化的范围之内，由此验证了优化算法的可行性。

5 结 语

本文将动平台位姿的六个参数直接看作为未知数，根据机构的约束条件，构造无约束优化模型，将原来计算复杂的非线性运动学正解问题转化为目标函数的寻优过程。相较于文献[20]中使用的建立位置参数模型的方法，本文的模型构造较为简单，且能将上平台中心的坐标矢量作为未知数直接求解，然后采用一种混沌序列调整惯性权重的改进粒子群算法求解出位姿正解的全部解。且由适应度函数的迭代进化曲线可知，改进的粒子群算法达到的收敛精度明显优于标准粒子群算法，收敛曲线的下降速度也快于标准粒子群算法。最后采用SolidWorks和Adams进行联合仿真试验，验证了优化算法的可行性。

[1] Zhang Hongli,Ren Tiantian,Pazilai M.Forward Position solution of 3-RPS in-Parallel Manipulator Based on Particle Swarm Optimization[C]//2014 26th Chinese Control and Decision Conference(CCDC),2014:4171-4177.

[2] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.

[3] 车林仙,何兵,易建,等.对称结构Stewart机构位置正解的改进粒子群算法[J].农业机械学报,2008,39(10):158-163.

[4] Greenivasan S V,Nanua P.Solution of the direct position kinematics problem of the general Stewart platform using advanced polynomial continuation[C]//Proceedings of the 22th ASME Mechanisms Conference,Arizona,1992:99-106.

[5] 王玉新,王仪明,柳杨,等.对称结构Stewart并联机器人的位置正解及构型分析[J].中国机械工程,2002,13(9):734-737.

[6] Wen Fuan,Liang Chonggao.Displacement analysis of the 6-6 Stewart platform mechanisms[J].Mechanism and Machine Theory,1994,29(4):547-557.

[7] 李树军,王玥.一种求解6-3构型并联机器人机构位置正解的逼近算法[J].机械科学与技术,2002,21(1):81-82,85.

[8] Dasgupta B,Mruthyunjaya T S.The stewart platform manipulator:a review[J].Mechanism and Machine,2000,35(1):15-40.

[9] 季晔,刘宏昭,原大宁,等.并联机构位置正解方法研究[J].西安理工大学学报,2010,26(3):277-281.

[10] Lee K M,Shah D K.Kinematic analysis of a three degrees of freedom in-parallel actuated manipulator[J].IEEE Journal of Robotics and Automation,1988,4(3):354-360.

[11] Lisandro J P,Roque J S,German R P,et al.Design and kinematic analysis of 3PSS-1S wrist for needle insertion guidance[J].Robotics and Autonomous Systems,2013,61(5):417-427.

[12] 刘伟锐,赵恒华.改进粒子群算法在并联机构位置正解中的应用[J].机械设计与制造,2014(2):181-183.

[13] 耿明超,赵铁石,王唱,等.基于拟newton法的并联机构位置正解[J].机械工程学报,2015,51(9):28-36.

[14] 杨传将,刘清,黄珍.一种量子粒子群算法的改进方法[J].计算技术与自动化,2009,28(1):100-103.

[15] 周俊,陈璟华,刘国祥,等.粒子群优化算法中惯性权重综述[J].广东电力,2013,26(7):6-12.

[16] 姜长元,赵曙光,沈士根.惯性权重正弦调整的粒子群算法[J].计算机工程与应用,2012,48(8):40-42.

[17] 许少华,李新幸.一种自适应改变惯性权重的粒子群算法[J].科学技术与工程,2012,12(9):2205-2208.

[18] Coelho L D S,Mariani V C.A novel chaotic particle swarn optization approach using Henon map and implicit filtering local search for economic load dispatch[J].Chaos Solitons & Fractals,2009,39(2):510-518.

[19] 刘玲,钟伟民,钱锋.改进的混沌粒子群优化算法[J].华东理工大学学报:自然科学版,2010,36(2):267-272.

[20] 贺利乐,刘宏昭,王朋.基于改进遗传算法的六自由度并联机器人位置正解研究[J].应用科学学报,2005,32(5):522-525.

OPTIMIZATIONALGORITHMOFFORWARDPOSESOLUTIONTOPARALLELROBOTANDITSSIMULATION

Li Muyuan Quan Huimin*Wu Guiqing

(CollegeofElectricalandInformationEngineering,HunanUniversity,Changsha410082,Hunan,China)

In this paper, 3-6 structure parallel manipulators are chosen as the research model. According to the constraint relation between configurations, an unconstrained optimization model is established for solving the forward position problem of the parallel platform. The complicated kinematics problem is transformed into a multiple nonlinear equations optimization process. In order to improve the convergence precision of the algorithm, an improved particle swarm optimization based on the chaotic sequence was proposed. Ergodic, stochastic and regular properties are the characteristics of chaos, which means it can track any state in a certain scope without repetition according to its regularity, using chaotic sequence to adjust the inertia weight was proposed in this paper, And used this improved particle swarm optimization to solve the forward position problem. Results of a numerical for the forward position analysis of the parallel platform show that, the improved particle swarm algorithm could solve all the position positive solutions, and compared to the standard particle swarm optimization algorithm can achieve higher convergence accuracy. At last, SolidWorks and Adams were used for co-simulation test. And the feasibility of the algorithm was verified.

Forward pose solution Particle swarm optimization algorithm Chaotic sequence Inertia weight Adams simulation

2016-12-08。 国家科技支撑计划项目(2014BAK08B01)。李穆远，硕士生，主研领域：人工智能算法。全惠敏，副教授。吴桂清，副教授。

TP242

A

10.3969/j.issn.1000-386x.2017.12.050