基于混合核平滑自编码器的分类器设计
2018-01-03吴小俊
刘 帆 吴小俊
(江南大学物联网工程学院 江苏 无锡 214122)
基于混合核平滑自编码器的分类器设计
刘 帆 吴小俊
(江南大学物联网工程学院 江苏 无锡 214122)
自编码器是一种重构输入数据的神经网络,具有较强的特征学习能力,被广泛地应用在各种分类任务中。为了将自编码器应用于分类任务中,研究一种基于混合核平滑自编码器的方法进行手写数字和人脸图像的分类。对不同核函数的权重进行比较,同时还将结果与稀疏自编码器进行比较。实验结果表明基于混合核的平滑自编码在一定的比例下可以获得比单个核函数更好的分类效果。
平滑自编码器 核函数 分类 重构
0 引 言
随着计算机信息处理技术的发展,深度学习在语音识别、图像分类和文本理解等众多领域的应用越来越多。而在实际应用中经常会碰到高维的数据,由于高维数据的普遍性,使得对高维数据降维的研究变得有意义。而其中的一种比较常用深度学习方法就是自编码器。
自从1988年Rumelhart[1]提出自编码器的概念以来,神经网络的发展有了很大的提高。Hinton[2]在2006年提出了深度置信网络(DBN),对基本自编码器进行了改进,利用微调显著改进了BP算法易陷入局部极小的情况。Bengio[3]在2007年提出了稀疏自编码器(SAE)的概念,在优化目标函数中加入稀疏性约束,发现输入数据的潜在结构,进一步加深了自编码器的研究。Vincent[4]在2008年提出了降噪自动编码器,通过腐蚀后的数据来进行重构,防止了过拟合现象的出现,并且取得了较好的结果。Rifai[5]在2011年提出了压缩自编码器,通过对编码函数进行约束,增加了自编码器的鲁棒性。Baldi[6]在2012年对自编码器与无监督学习之间的关系进行了讨论,并且介绍了如何利用自编码器构造不同种类的深度模型。Liang[7]在2014年提出了平滑自编码器,通过重构样本的k近邻,而不是以往的重构样本本身,保持了数据的流形结构,增加了模型的鲁棒性。然而在确定k近邻的权重的时候,仅仅只是使用了高斯核函数作为权函数,只是利用了数据特征的局部性,而没有考虑到数据特征的全局性。因此,本文引入了混合核函数作为k近邻的权函数,这样学习到的特征不仅在局部上有较好的鲁棒性,而且在全局上也有一定的鲁棒性,同时也保持了数据的流形结构。
1 自编码器网络结构
1.1 基本自编码器
已知X={x1,x2,…,xn}∈RD×n为包含n个数据的高维数据集,其中xi是第i个D维数据。Y={y1,y2,…,yn}∈RD×n为X的重构数据集。自编码器网络结构如图1所示。整个网络由编码器(encoder)和解码器(decoder)两个网络组成。编码器的作用就是对输入数据进行降维处理,得到数据的码字表示h。解码器相当于编码器的逆过程,把数据的码字表示h重构成高维数据。 编码器和解码器之间存在一个交叉部分,称之为码字层,它是整个网络的核心部分,能够表示高维数据的本质结构。
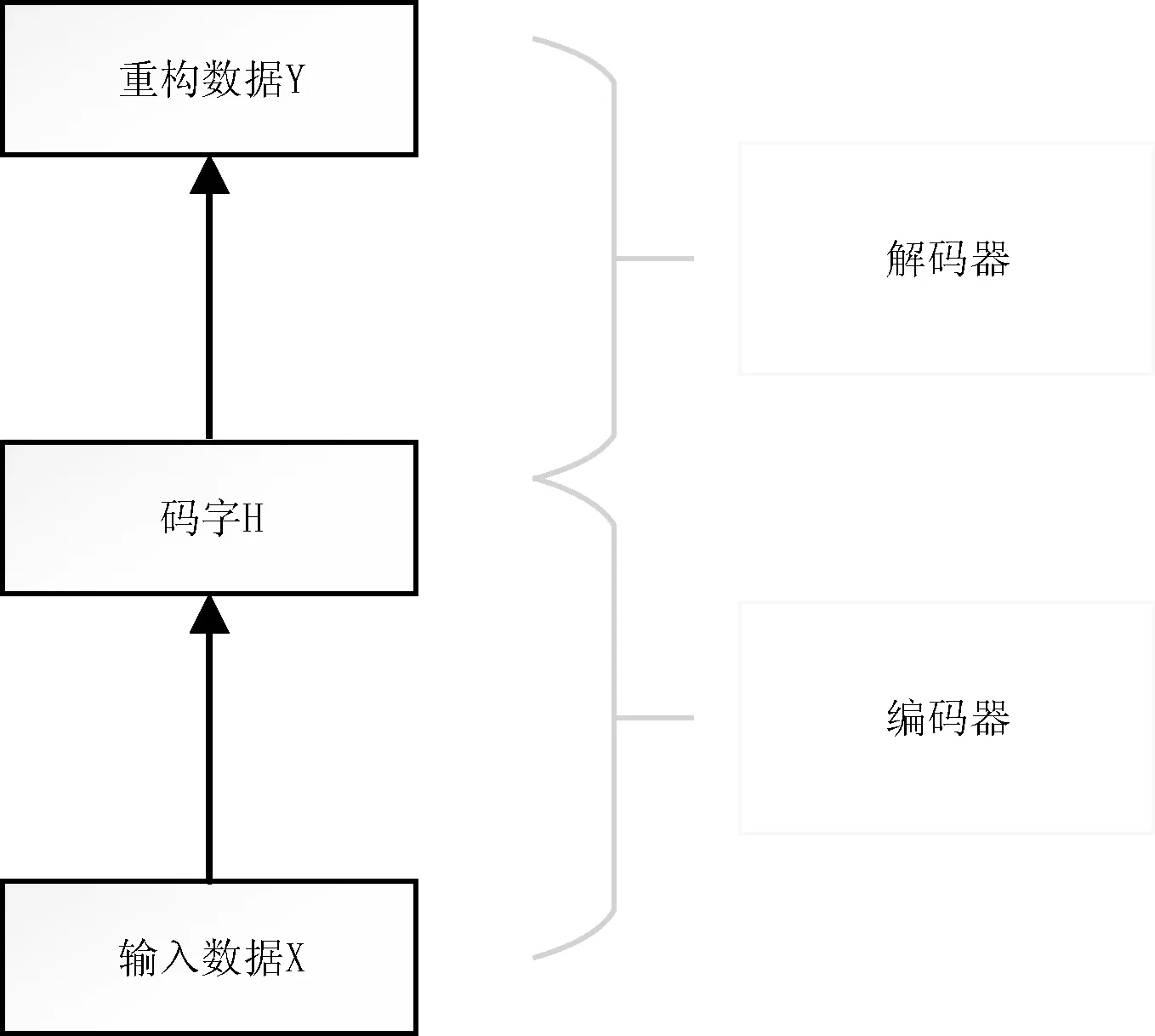
图1 自编码器网络结构图
自编码器的工作原理如下:首先初始化编码器和解码器两个部分的权值,然后依据原始数据和重构数据之间的误差最小化对自编码器网络进行训练。
得到的码字[11]表示为h=f(Wx+bh),其中,f(x)=(1+exp(-x))-1,bh为码字层的偏置。然后,使用一个线性解码器对h进行解码,得到y=WTh+bv,其中,bv为输出层的偏置,y为原始数据的重构。
1.2 平滑自编码器
从自编码器网络结构图中就可以看出自编码器重构的是原始输入,而没有考虑到数据之间的内在结构。数据较小的波动可能导致结果产生大的波动,因此模型的鲁棒性差。Liang[7]提出了平滑自编码器,对于一个数据xi,它重构的是一个集合Ωi={xj,xk,…},这个集合是xi的k近邻,在进行表示学习的同时保持了流形结构,保证了局部邻居之间的相似性。在确定k近邻的权重时,使用的是高斯核函数,在一定程度上表示的是数据的局部信息。
1.3 混合核平滑自编码器
由于平滑自编码器在确定权函数时,仅仅只是使用了单个光滑的核函数,不能同时考虑到局部和全局的信息。本文运用多个核函数来确定权函数,同时兼顾了局部和全局的信息,从而达到对数据集更好的分类。本文采用了高斯核函数、多项式核函数和线性核函数的组合形式作为权函数,对其中的两两组合形式和三个的组合形式进行了研究,进而确定混合核函数的有效性。
1.3.1 高斯核函数和线性核函数组合
高斯核函数[9]具有良好的局部性质,只有相距很近的数据点才对核函数的值有影响,但是其全局性较差,不具有好的泛化性质,其泛化能力随着带宽的增大而减小。而线性核函数[8]具有一定的全局性,在寻找权函数的过程中,在高斯核函数的基础上加入线性核函数在一定程度上增加了权函数的全局性。权函数的表达式如下:
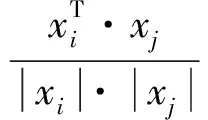
(1)
式中:xi和xj分别为第i个和第j个数据点,σ为高斯核函数的带宽,控制了函数的径向作用范围,m∈[0,1]。
1.3.2 高斯核函数和多项式核函数组合
多项式核函数[10]具有良好的全局性,即使相距很远的数据点都可以对核函数产生影响,具有良好的泛化能力,但是其局部性较差。权函数的表达式如下:
(2)
式中:q为多项式的次数。q越大,映射的维数越高,计算量也越大。q越小,映射的维数越低,计算量也越小,同时也降低了学习精度,m∈[0,1]。
1.3.3 多项式核函数和线性核函数组合
多项式核函数和线性核函数表示的都是全局信息。权函数的表达式如下:
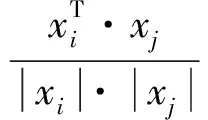
(3)
式中:m∈[0,1]。
1.3.4 高斯核函数、多项式核函数和线性核函数组合
权函数的表达式如下:
(4)
式中:m∈[0,1],n∈[0,1-m]。
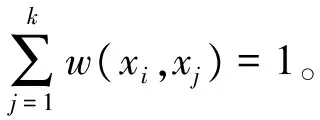
(5)
式中:Z是标准化项,Ωi是xi的k近邻集合。
2 混合核函数的实现
本文首先对两个核函数的组合进行了实验,实验的数据集为MNIST-BASIC和Extended YaleB。两个核函数不同的比例产生了不同的重构误差和分类误差。对于MNIST-BASIC数据集,采用的网络结构是(784,1 000,784)。而对于Extended YaleB数据集,采用的网络结构是(1 024,1 000,1 000,1 024)。
2.1 高斯核函数和线性核函数组合
实验中运用式(1)对k近邻的权重进行计算。当m=0.7时,重构结果见图2。(a)图是原始数据,(b)图是使用高斯核和线性核函数的混合核函数进行100次迭代后的重构结果,(c)图是在只使用高斯核函数进行100次迭代后的重构结果,(d)图是在只是用线性核函数进行100次迭代后的重构结果。在不同的比例下,不同数据集的分类误差的结果见表1。表中第1列表示的是m的大小。最后的三行为单独的高斯核函数和单独的线性核函数作为权函数时产生的误差和稀疏自编码器的分类误差。

图2 手写数字的重构结果
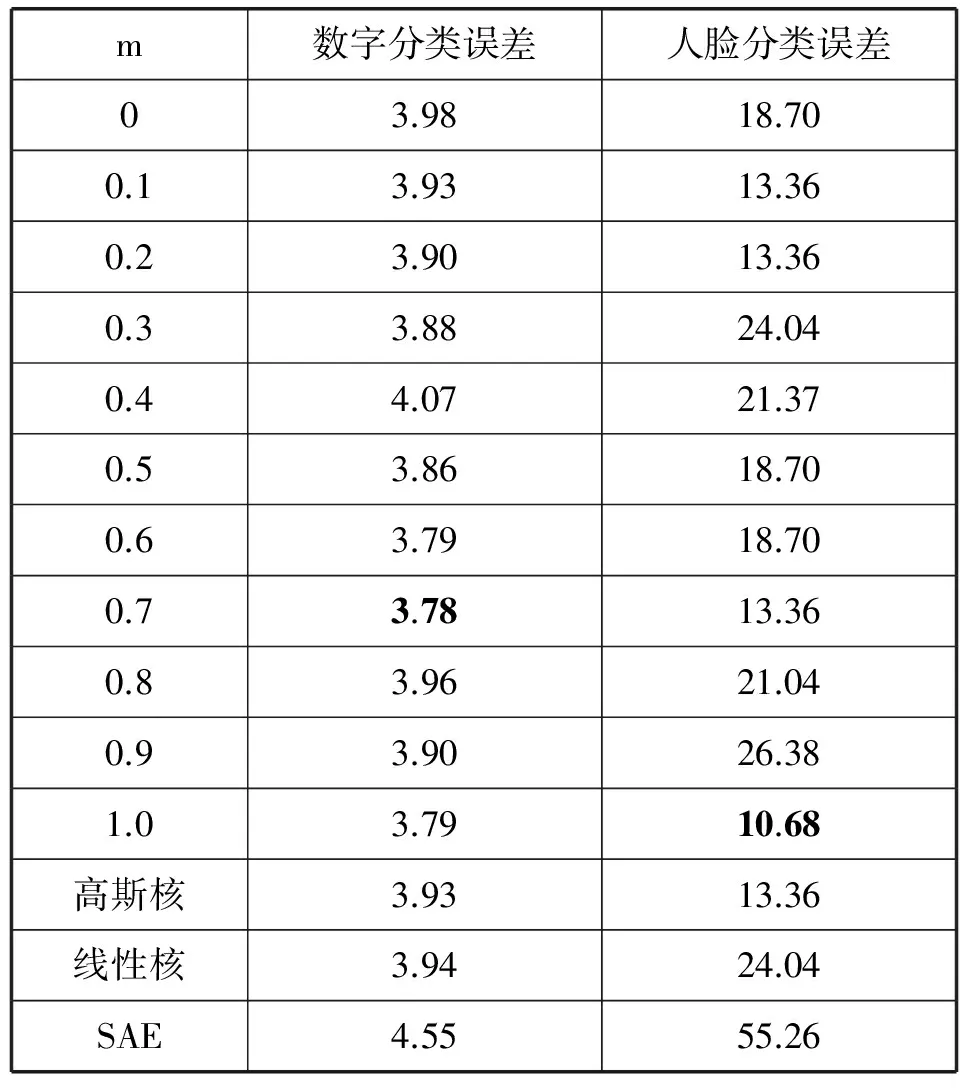
m数字分类误差人脸分类误差03.9818.700.13.9313.360.23.9013.360.33.8824.040.44.0721.370.53.8618.700.63.7918.700.73.7813.360.83.9621.040.93.9026.381.03.7910.68高斯核3.9313.36线性核3.9424.04SAE4.5555.26
对于分类误差,不同比例的混合核函数的构建在大多数情况下都有了一定程度的减小。表中加粗的是最小的误差值。
从表中可以看到,对于MNIST-BASIC,当m=0.7时,混合核函数作为权函数产生的分类误差最小,而这个值也比单独的核函数作为权函数时产生的分类误差小。对Extended YaleB,当m=1.0时,分类误差最小,这个值同样比单独的核函数作为权函数时产生的分类误差小。而混合核函数和单核核函数作为权函数得到的重构效果和分类效果都要比SAE好。由于线性核函数在一定程度上增加了核函数作为权函数的全局性,在保证数据流形的基础上,提取的特征具有更好的抗扰动性,鲁棒性更好。
2.2 高斯核函数和多项式核函数组合
下面通过实验考察了高斯核函数和多项式核函数之间的关系对重构和分类的影响。同时也对多项式的次数进行了研究,根据实验结果选择多项式的次数为9。在多项式次数为9的前提下,采用式(2)进行两个核函数的比例研究。重构结果见图3,(a)图是原始数据,(b)图是使用高斯核函数和多项式核函数的混合核函数进行了100次迭代后的重构结果,(c)图是只使用高斯核函数100次迭代后的重构结果,(d)图是只使用多项式核函数100次迭代后的重构结果。误差结果见表2。表中加粗的为误差的最小值。表中第一列为m的大小。最后三行是单独的高斯核函数和单独的多项式核函数作为权函数时产生的误差和SAE分类误差。

图3 手写数字的重构结果

m数字分类误差人脸分类误差03.9523.620.13.9513.020.23.8621.370.33.9018.360.43.8916.030.53.9318.700.63.9516.030.74.0421.040.83.8318.280.93.8718.701.03.9418.70高斯核3.9313.36多项式核4.0313.36SAE4.5555.26
第2列是数据集为MNIST_BASIC时的分类误差,在m=0.8时,分类误差最小,这个值也比单独的高斯核函数和单独的多项式核函数所产生的分类误差小。最后一列是数据集为Extended YaleB 时的分类误差,在m=0.1时,混合核函数作为权函数时,产生的分类误差最小,当然也比单独的核函数作为权函数时产生的分类误差小。这就说明了在一定比例下的混合核函数要比单独的核函数作为权函数好。同时也说明了在权函数中加入全局信息,可以一定程度上保证数据的流形结构,增加了模型的鲁棒性。
2.3 多项式核函数和线性核函数组合
多项式的次数可以有多种选择,在这里选定为5,然后使用式(3)对两个核函数的比例进行研究。分类误差见表3。表中加粗的为误差最小的值。表中第1列为1-m的大小,最后三行是单独的多项式核函数和线性核函数作为权函数时的分类误差和SAE的分类误差。
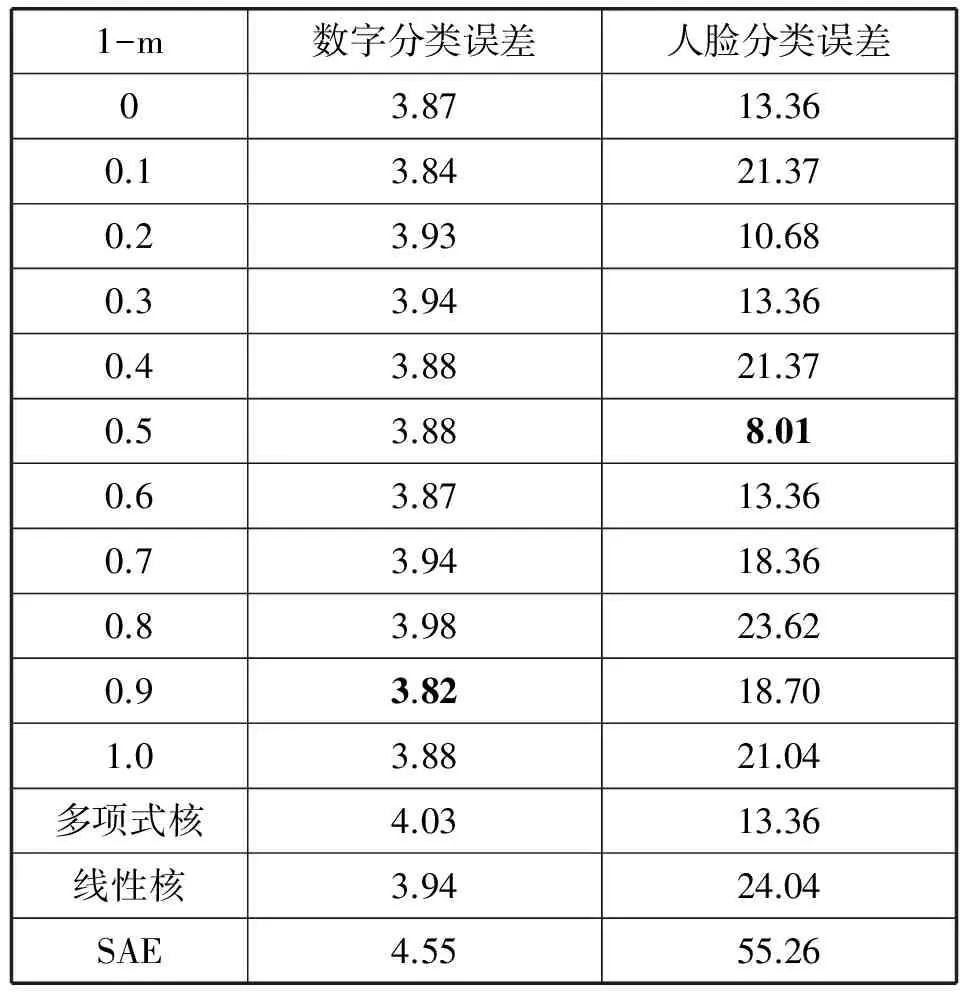
表3 多项式核、线性核函数组合的比例研究与单核和SAE的比较
对MNIST_BASIC数据集,基本上任何比例下的分类误差都要比单独的小。而对Extended YaleB数据集,当m=0.5时,得到的分类误差最小,同时也小于单独的核函数作为权函数时产生的分类误差。这两个核函数都在一定程度上表示的是全局信息,两个混合表示的全局信息多于单个的,因此效果要比单个的要好。但与上面的结果比较可知,只有全局信息并不能得到很好的结果,只有在确定权函数时增加局部信息和全局信息才能得到好的结果。这就说明了在保持了数据流形的基础上,适当加入全局信息可以得到更好的结果。
2.4 高斯核函数、多项式核函数和线性核函数组合
在研究了两个核函数比例间的影响后,本文使用式(4)对这三个核函数之间的关系进行了研究。为避免参数过多,这里选定多项式的次数为5。由于这三个核函数之间的比例关系复杂,产生的误差矩阵是一个上三角矩阵。详细结果见表4。表中第1行是n的大小,第1列是m的大小。从表中可以看到,对于每一行数据,分类误差达到最小时,线性核函数和多项式核函数的比例都不同。当这三个比例参数任意一个为0时,就相当于两个混合核的情况。由于连接权重初始化的随机性,导致了三个核产生的误差结果与双核产生的误差结果的不一致性,但是差距是在可接受的范围内。
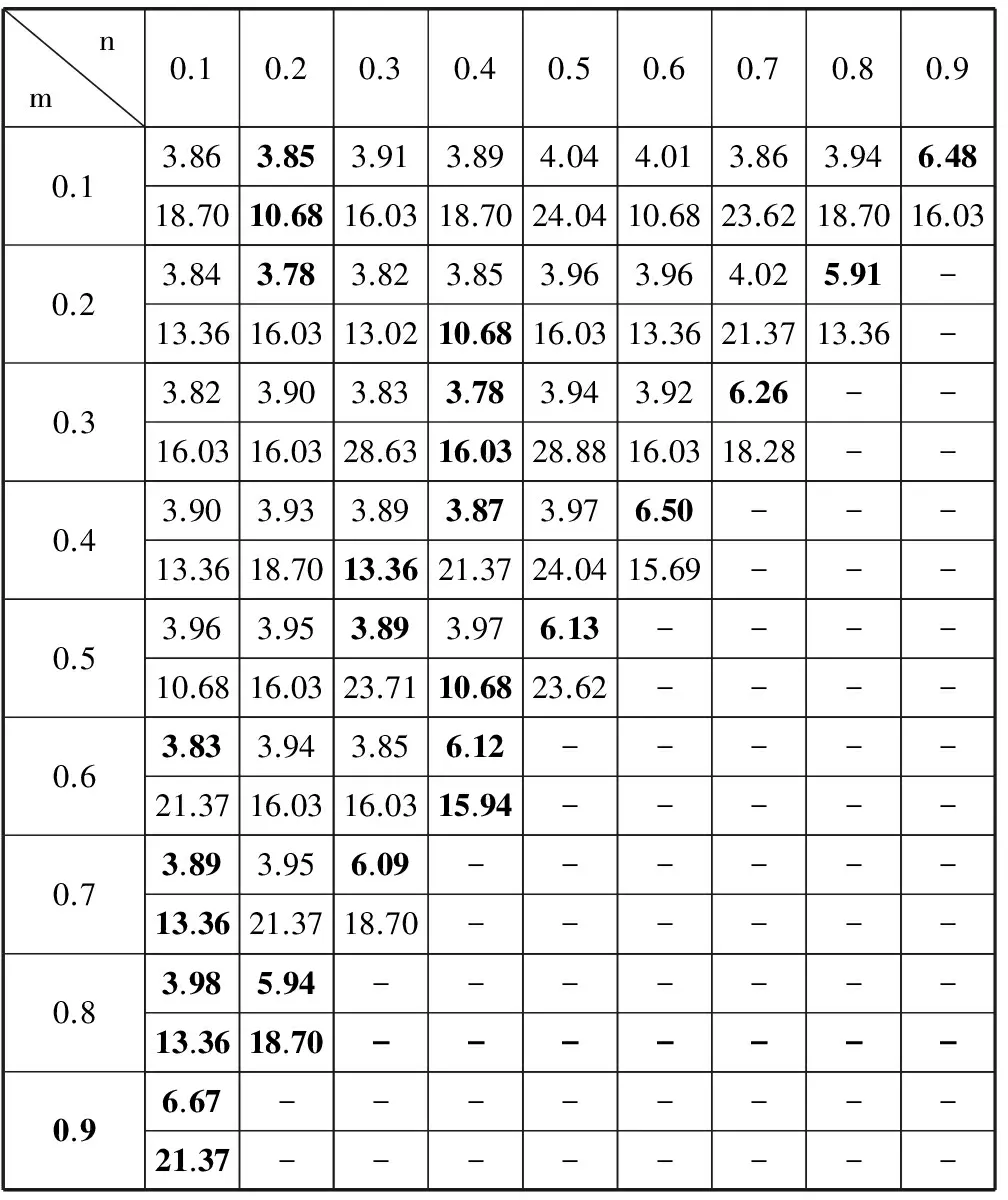
表4 高斯核函数、线性核函数和多项式核函数组合的比例研究
对于MNIST_BASIC数据集,表中最后一个数据都突然变大,这是三个核函数选了两种极端情况。说明混合核函数的研究需要对多种情况进行研究。
对于Extended YaleB 数据集,并没有出现手写数据集那样的误差突然增大的情况,然而在m=0.5,n=0.1时,分类误差为10.68,而在单个高斯核函数作为权函数的情况下,分类误差为18.36。从数据来看,结果有了一定程度的提升。这三个混合核函数作为权函数与单个高斯核函数相比,增加了局部信息和一定量的全局信息,因此在一定程度上可以改进分类结果。
在同样的实验条件下,两个组合中高斯核函数和线性核函数的组合得到的分类误差最小,多项式核函数和高斯核函数的组合得到的分类误差最大。线性核函数和多项式核函数都含有数据特征的全局性,但是由于多项式次数选取的不同,对实验结果影响很大,因此在实验时必须选择合适的次数,这样才能得到好的结果。而多项式核函数和线性核函数的组合基本上利用的是数据特征的全局性,因此分类效果要差于高斯核和线性核函数的组合形式。三个核函数的组合形式的分类效果要优于只使用数据特征的局部性或全局性的核函数。
3 结 语
本文在平滑自编码器的基础上提出了一种混合核平滑自编码器,并将混合核平滑自编码器用于手写数据集和人脸数据集的识别,实验表明,在一定的混合比例下,混合核平滑自编码器比单核平滑自编码器具有更好的重构和分类能力。
混合核平滑自编码器允许多种不同的核函数进行组合,根据每个核函数代表的物理意义选择不同的组合,得到的混合核有不同的含义。如何根据实际应用选择核函数的组合、如何自动地确定最优权函数的权重是今后需要研究的问题。
[1] Rumelhart D E,Hinton G E,Williams R J.Learning representations by back-propagating errors[J].Nature,1986,323(6088):533-536.
[2] Hinton G E,Osindero S,Teh Y W.A fast learning algorithm for deep belief nets[J].Neural computation,2006,18(7):1527-1554.
[3] Bengio Y,Lamblin P,Popovici D,et al.Greedy layer-wise training of deep networks[C]//NIPS’06 Proceedings of the 19th International Conference on Neural Information Processing Systems,2006:153-160.
[4] Vincent P,Larochelle H,Bengio Y,et al.Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th international conference on machine learning.ACM,2008:1096-1103.
[5] Rifai S,Vincent P,Muller X,et al.Contractive auto-encoders: Explicit invariance during feature extraction[C]//Proceedings of the 28th international conference on machine learning (ICML-11).2011:833-840.
[6] Baldi P.Autoencoders,unsupervised learning and deep architectures[C]//International Conference on Unsupervised and Transfer Learning Workshop.JMLR.org,2011:37-50.
[7] Liang K,Chang H,Cui Z,et al.Representation Learning with Smooth Autoencoder[C]//Asian Conference on Computer Vision.Springer International Publishing,2014:72-86.
[8] 王行甫,俞璐.混合核函数中权重求解方法[J].计算机系统应用,2015,24(4):129-133.
[9] 王国胜.核函数的性质及其构造方法[J].计算机科学,2006,33(6):172-174.
[10] 左森,郭晓松,万敬,等.多项式核函数SVM快速分类算法[J].计算机工程,2007,33(6):27-29.
[11] Kamyshanska H,Memisevic R.On autoencoder scoring[C]//Proceedings of the 30th International Conference on Machine Learning (ICML-13),2013:720-728.
DESIGNOFCLASSIFIERBASEDONHYBRIDKERNELSMOOTHAUTOENCODER
Liu Fan Wu Xiaojun
(SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi214122,Jiangsu,China)
Autoencoder is a kind of neural network that reconstructs input data and has strong learning ability which has been widely applied to many kinds of classification tasks. In order to apply autoencoder to classification tasks, this paper proposes a method based on hybrid kernel smooth autoencoder to classify handwritten numerals and face images. We compared the weights of different kernel functions, and compared the results with sparse self-encoders. The experimental results show that hybrid kernel based smooth autoencoder in a certain ratio can obtain better classification results than the single kernel function autoencoder.
Smooth autoencoder Kernel function Classification Reconstruction
2017-03-05。国家自然科学基金项目(61672265,61373055)。刘帆,硕士生,主研领域:人工智能与模式识别。吴小俊,教授。
TP3
A
10.3969/j.issn.1000-386x.2017.12.046
