有轨电车动态限界计算软件设计与实现

杨 宇 张济民 耿 跃

1(同济大学铁道与城市轨道交通研究院 上海 201804) 2(上海汇煦交通科技有限公司 上海 201108)

有轨电车动态限界计算软件设计与实现

杨 宇1张济民1耿 跃2

1(同济大学铁道与城市轨道交通研究院 上海 201804)2(上海汇煦交通科技有限公司 上海 201108)

针对目前没有形成有轨电车结构和模块编组特点的限界计算方法的现状，提出有轨电车动态限界(水平限界)算法。该算法基于解析几何方法，结合列车动力学分别推导出有轨电车在直线和曲线运行情况下以及有、无强侧向风情况下车体横向偏移量，计算出车辆动态限界。同时通过Matlab软件开发平台设计了有轨电车动态限界计算软件。该软件具有导入计算参数与导出计算结果的功能，通过软件计算，可以得到不同运行情况下有轨电车车辆横向限界值。最后给出计算实例来对算法进行验证，实验结果表明,该算法满足实践工程需求。该软件可供有轨电车车辆限界设计参考使用。

有轨电车 动态限界 解析几何 Matlab GUI

0 引 言

自1899年以来，有轨电车在我国的发展历经了引进—衰落—再发展的阶段[1]，目前，现代有轨电车以诸多优势取代了旧式有轨电车，在国内得到较为广泛的应用。据《2014年中国城市轨道交通市场发展报告》预测，2015年中国现代有轨电车新增运营线路里程达133.43公里，建设规模大幅增长。其中，北京、上海、广州、成都等诸多省市积极规划建设有轨电车系统[2]。但总体来看，现代有轨电车在我国尚处于初步发展阶段，尚未建立起系统的技术标准，车辆设计理念和方法不能简单照搬地铁的相关规范，在起步阶段需要建立起结合我国国情的现代有轨电车系统的国家标准，用以指导有轨电车系统的发展。

截至2016年11月，有轨电车系统的相关规范《现代有轨电车交通工程技术标准》正在接受审查，但是技术标准中关于有轨电车车辆限界的相关规定只列举了原则性的要求，未明确给出限界的计算方法。目前，用于计算有轨电车车辆限界的方法大多参考《城市轨道交通建设和运营规则》(BOStrab)和《地铁限界标准》(CJJ 96—2003)，其设计理念基本与地铁限界设计标准一致[3-5]。由于有轨电车的运行环境与地铁有很大差异，因此借用地铁限界设计理念计算有轨电车限界的做法是否准确适用，仍需实践检验。

本文提出一种新型的基于解析几何方法的有轨电车车辆限界(横向部分)计算算法，相对于参考地铁限界计算的方法，涉及到的参数较少，更加简洁方便。由于不同型号的有轨电车各项参数不同，但计算过程基本相同，为避免重复计算过程，利用Matlab软件在复杂数值分析、运算方面的明显优势，采用Matlab软件自带的图形用户界面GUI(Graphical User Interface)开发可视化界面。通过该软件可以很方便地实现限界的计算过程，用户只需输入相应车型的参数，选定相应运行情况，无需掌握代码具体内容，便可以快捷得到动态限界计算结果[6]。

1 有轨电车动态限界计算方法

当有轨电车在线路上运行时，计算车体横向动态限界需考虑到列车的横摆和侧滚运动，经分析计算得到车体最大偏移点处的内、外侧限界，最终相加得到总限界值。有轨电车动车和拖车横摆示意图如图1所示，侧滚示意图如图2所示。

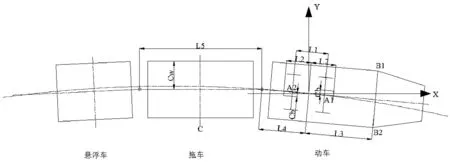
图1 车体横摆示意图

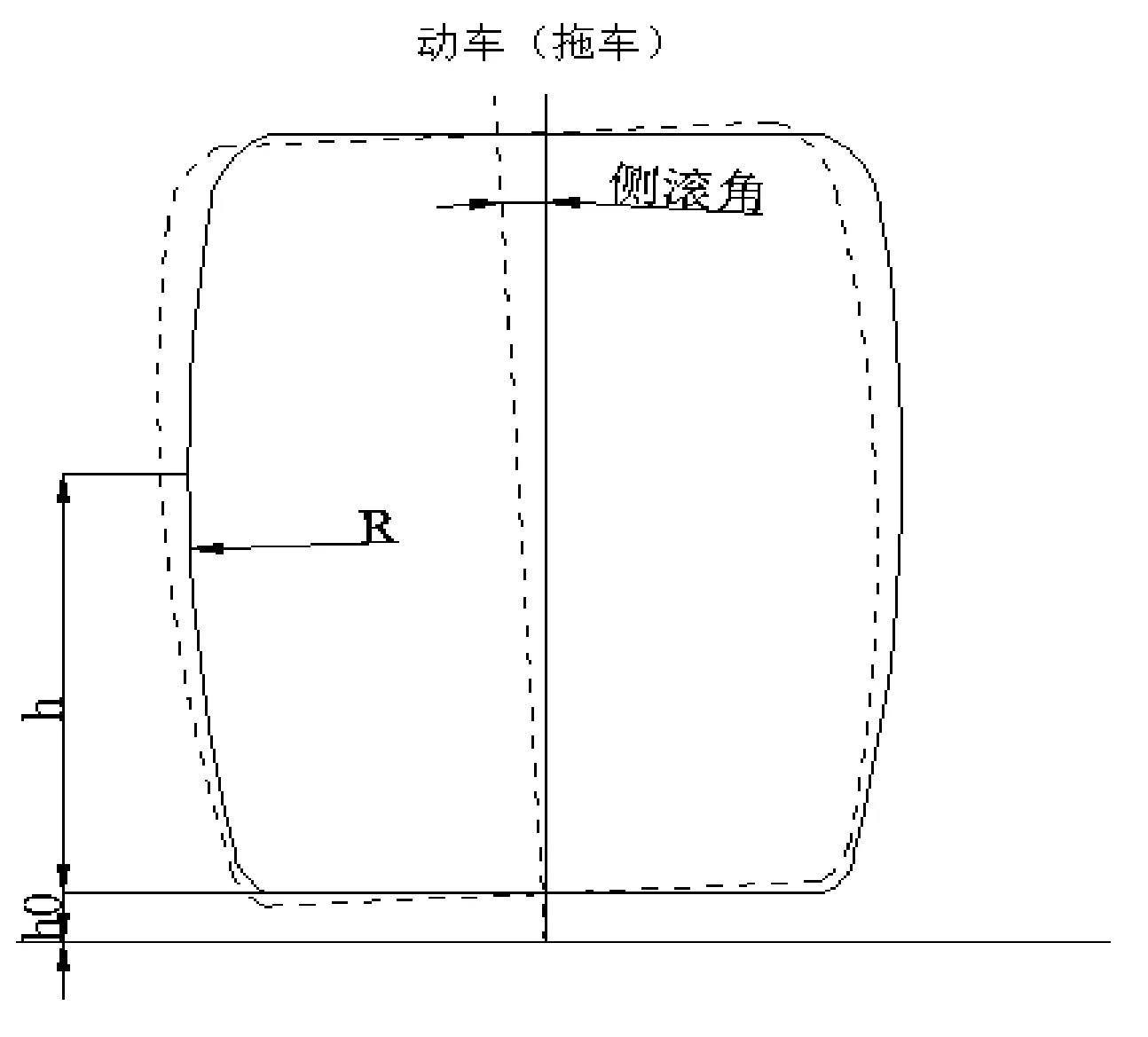
图2 车体侧滚示意图

无论列车横摆和侧滚运动方向如何，外侧限界总取决于动车的B1点，无需考虑拖车与悬浮车；而计算内侧限界时，拖车的内侧限界需要与动车的内侧限界比较，找出动车和拖车内侧限界的较大值[5]，作为车体内侧限界。

考虑横摆运动的影响，车体外侧限界的偏移最大点位于动车的端部截面的一点处，即图1中B1点。图1中A1、A2点分别是转向架两车轴中心线与线路中心线的交点，以转向架中心点为坐标原点建立直角坐标系。

根据所给参数和三角形相似计算出A1、A2点的坐标。当车辆在直线运行时，可根据两点坐标计算求得偏移角，根据相似三角形定理可分别得到B1点横向偏移量以及B1点据车体中心线的距离，即直线运行工况下横摆作用的外侧动态限界。

当车辆在曲线运行时，需要找出曲线的圆心坐标及B1点距圆心距离，后者减去曲线半径(外摆)或曲线半径减去后者(内摆)，即为曲线运行工况下横摆作用的外侧动态限界。

当通过大半径曲线时，动车有可能向曲线内侧摆动，当曲线圆点横坐标大于前部端墙到车体中心纵向距离时，就需要考虑动车车体内侧轮廓点造成的限界。找出曲线的圆心坐标及B2点距圆心距离，曲线半径减去后者即为动车内侧动态限界，并可以确定车体向内偏移的距离。利用铰接点与圆心坐标即可求出拖车内侧动态限界，以及拖车向内偏移的距离。进行比较后，较大值作为横摆作用的内侧动态限界。

考虑侧滚运动的影响，以线路水平方向为横轴，列车垂向中心线为纵轴，建立直角坐标系，如图2所示。在考虑横摆影响车体产生偏移的情况下，假设车体侧墙为曲面，只需计算得到车体侧墙曲面的圆点坐标，用曲面半径减去(外侧侧滚)或加上(内侧侧滚)圆点横坐标值即可最终得到最大偏移点处的内外侧动态限界。

当有轨电车以空车运行时，计算动态限界只需考虑横摆运动的影响；以重车运行时，需要考虑横摆和侧滚的共同影响。

在有轨电车实际运行时，还可能会受到强侧向风的影响。此时，车体产生较大的横向位移，导致横向止挡与构架接触，限制车体更大的横向位移。因此在考虑横摆的影响时，A1、A2点的纵坐标只需考虑一系悬挂横向位移和车体与转向架横向止挡间隙两项参数。其余步骤与上述计算方法相同。

2 限界计算软件实现

2.1 软件概述

有轨电车动态限界计算软件采用Matlab的GUI模块进行编写。该软件采用了本文提出的新型的基于解析几何的动态限界计算方法，主要功能就是计算有轨电车动态限界范围。该软件很好地避免了人工计算的重复繁杂和带来的误差，节省了人力物力。目前软件可针对不同车型的有轨电车进行动态限界的计算。图3给出了有轨电车动态限界计算软件的计算流程。

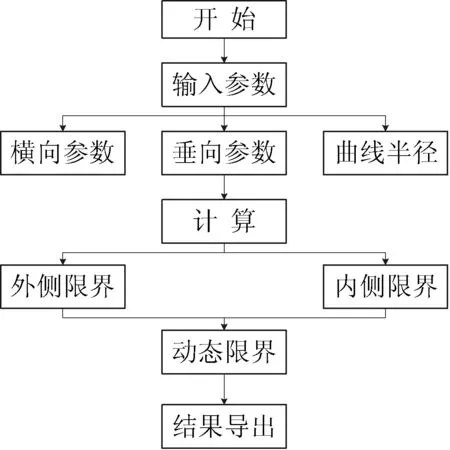
图3 软件计算方法流程图

2.2 软件主界面

Matlab下的GUI图形用户开发环境GUIDE提供了一系列的开发工具，设计者只需根据功能需要自由调用、组合不同控件，布局完成后进行各个控件的程序代码编写[7]。有轨电车动态限界计算软件中每个GUI界面设计均包含有后缀名为.fig的界面布局文件和.m的运行函数文件。

软件主界面如图4所示。主界面主要包括2个Axes用于放置背景图；“横向参数”、“垂向参数”、“计算”3个按钮；“曲线半径”静态文本框及其后的可编辑文本框；“强侧向风”的静态文本框和单选按钮。

图4 软件主界面

对应于每个按钮都可以在对应的.m文件中找到回调函数，对其进行代码编写以实现相应的功能，此处为调用对应的GUI界面。

线路曲线半径在可编辑文本框中输入，其对应的回调函数为：

r=str2num(get(handles.edit14,′string′));

单选按钮选定后将侧向风的有关数据赋值给wind并导入到计算过程中；其回调函数为：

wind=get(handles.wind,′value′);

在主界面的.m文件中包含了所有的计算过程。当输入的参数保存在对应的mat数据文件中，“计算”按钮可将各个数据分配至对应的参数名称中，通过文件后面的计算得到相应的限界计算结果，储存在Matlab数据库中。另外定义一个result_data.m函数文件用于调用结果数据，并将数据导入进另一个result.m文件，用于结果的显示。其中，点击“计算”按钮即可调用result.m文件对应的GUI界面。计算过程的流程图如图5所示。

图5 计算过程流程图

2.3 参数输入与输出

主界面中的2个参数输入按钮分别对应2个横向和垂向参数输入的GUI界面，如图6-图7所示。每个参数输入的GUI界面分别包括1个Axes用于放置各项参数的示意图；若干个显示参数名称的静态文本框以及对应的可编辑文本框，用于输入不同参数值；1个“确定”按钮。

图6 横向参数输入界面

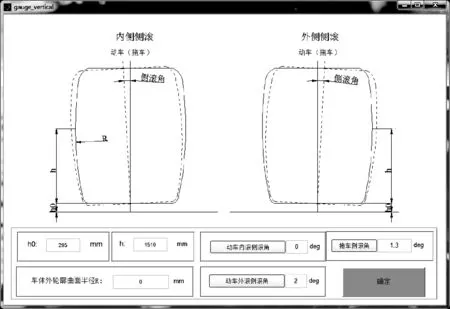
图7 垂向参数输入界面

每一个静态文本框都可以直接在GUI图形设计编辑界面里操作完成；每一个可编辑文本框的回调函数格式为：

L=str2num(get(handles.edit1,′string′));

右下角的“确定”按钮用于保存输入的参数值并关闭此界面，返回主界面。

2.4 计算结果

主界面的计算按钮对应于另外一个显示结果的GUI界面，如图8所示。界面包括1个Axes用于放置限界结果示意图；若干个静态文本框用于结果参数名称设置及对应的可编辑文本框用于结果数据的显示；“导出”和“返回”2个按钮。

图8 计算结果界面

结果输出界面对应result.m文件，只需调用存入了结果数据的result_data.m文件，将结果显示到对应的可编辑文本框中即可。

“导出”按钮可以用于计算结果数据的导出并保存，使用者可以自行定义保存路径，结果数据以.xls格式保存。“返回”按钮用于返回主界面。

3 实例验证

本文采用某型号有轨电车为例，将其相关参数输入软件进行计算，得出其动态限界，验证软件的可行性和准确性。

某型号有轨电车的相关参数详见表1。

表1 某型号有轨电车相关参数

根据表1中的参数计算该车型有轨电车的动态限界。设定曲线半径为150 m，有强侧向风的情况下，计算结果为车体外侧动态限界值为1 485.7 mm，内侧动态限界值取拖车内侧限界，为1 443.9 mm，总限界值为2 929.6 mm。当设定曲线半径为150 m，无强侧向风情况下运行，计算结果为车体外侧动态限界值为1 509.4 mm，内侧动态限界值取拖车内侧限界，为1 459 mm，总限界值为2 968.4 mm。由计算结果可知，软件的有轨电车动态限界算法具有一定的可行性，能够满足实际工程的需求。

4 结 语

本文基于解析几何的方法，结合有轨电车动力学提出一种新型的计算有轨电车动态限界的算法，具有一定的现实指导意义。在此基础上，通过Matlab GUI模块将算法整合出一个图形用户界面，设计成有轨电车动态限界计算软件，并通过实例计算验证了该软件的有效性，可供有轨电车车辆限界设计参考使用。

[1] 李元坤,苗彦英.国外现代有轨电车建设发展的启示[J].城市轨道交通研究,2013,16(6):29-32.

[2] 中规院交通院综合所.2015年中国现代有轨电车现状一览[J].中国轨道交通杂志,2015-6-29.

[3] 叶芹禄.有轨电车车辆限界的计算方法[J].铁道勘测与设计,2014(6):1-3.

[4] 王嘉鑫.浮动车体型有轨电车车辆限界(横向部分)计算方法分析[J].地下工程与隧道,2015(1):44-46,50.

[5] 吕凤梅,赵建秋,闫晓明,等.100%低地板现代城市有轨电车限界和小曲线通过能力分析[J].铁道车辆,2013,51(9):5-7.

[6] 秦辉,席裕庚.基于Matlab GUI的预测控制仿真平台设计[J].系统仿真学报,2006,18(10):2778-2781.

[7] 王华乔.基于MATLAB GUI的自动控制原理仿真软件设计[J].计量与测试技术,2011,38(2):12-14.

[8] 李连峰,樊金凤,周菁.铁路机车车辆限界规校准方法研究[J].铁道技术监督,2016,44(11):21-23,26.

[9] 李磊,张茂帆,李芾,等.悬挂单轨交通限界计算方法研究[J].铁道机车车辆,2016,36(1):119-126.

[10] 张恺,张玉钧.基于Matlab-GUI的衍射图像分析[J].计算机应用与软件,2011,28(3):243-245,281.

DESIGNANDIMPLEMENTATIONOFDYNAMICGAUGECALCULATIONSOFTWAREFORTRAMS

Yang Yu1Zhang Jimin1Geng Yue2

1(InstituteofRailTransit,TongjiUniversity,Shanghai201804,China)2(ShanghaiHuixuTransportationScienceandTechnologyCo.,Ltd.,Shanghai201108,China)

Because there is no calculation method of dynamic gauge for trams with its structure and module marshalling characteristics, this paper proposes a calculation method of dynamic gauge (horizontal gauge) for trams. Based on analytic geometry method and train dynamics, this algorithm derived the lateral offset of car-body when trams operated under different circumstances including in line and curve and with a strong side wind or without strong side wind, then the dynamic gauge of trams was calculated. At the same time, the dynamic gauge calculation software for trams was developed through the Matlab software platform. This software has functions of import calculation parameters and export calculation results. Through this software, the lateral gauge values of trams under different situations can be calculated. Experimental results show that this calculation method can meet the needs of practical engineering. Therefore this software can be used as references in vehicle gauge design for trams.

Trams Dynamic gauge Analytic geometry Matlab GUI

2017-02-22。杨宇，硕士生，主研领域：轨道车辆结构及动力学，列车空气动力学。张济民，教授。耿跃，高工。

TP3

A

10.3969/j.issn.1000-386x.2017.12.026