MatLab在成都地震台数字地震记录中的应用

何思源，刘华娇，徐文海，钟李彬，董立杰

(成都地震基准台 四川省地震局，四川 成都 611730)

MatLab在成都地震台数字地震记录中的应用

何思源，刘华娇，徐文海，钟李彬，董立杰

(成都地震基准台 四川省地震局，四川 成都 611730)

成都地震基准台数字台网中记录到的小震级地震数据中有的包含较为严重的干扰，本文利用MatLab计算软件对数字地震记录进行频谱分析，设计FIR、IIR两种类型滤波器对这些干扰数据进行滤波，对两种不同类型的滤波器的应用结果进行对比分析。通过滤波器处理后干扰得到有效消除，数据质量得到显著提高，分析认为2～4 Hz的干扰信息是成都地震台地震记录质量不佳的重要原因，这对于今后的地震数据分析工作具有一定的参考价值。

MatLab；数字地震记录；干扰信息；滤波器

成都地震基准台目前使用了JCZ-1型和JCZ-1T型两套甚宽频带地震计[1]。其中JCZ-1是分体装置，由一个垂向和两个水平向地震计构成，频带宽为20 Hz-DC，JCZ-1T型是JCZ-1型的改进型，是三分量一体机，地震计频带宽为50 Hz-DC。地震计数字化极大丰富了观测的信息量，同时人们又面临如何去处理和使用这样规模庞大的数字化观测资料的问题。地震计仪器在数据采集的时候，也会采集到很多干扰信号，这些干扰严重影响了观测地震波数据的质量，因此需要对这些干扰加以排除[2]。MatLab软件是一套进行科学计算的高性能软件，兴起于20世纪70年代，在传统的C语言和FORTRAN计算语言的基础之上，MatLab语言以更接近数学公式的表达方式，给用户提供了最简洁最直观的数字计算开发环境[3]。本文介绍在MatLab软件中利用快速傅里叶变换(FFT)方法实现有限序列长度的地震波形记录频谱分析，以及FIR、IIR两种滤波器的设计原理和应用于成都台测震数据后的对比分析。

1 快速傅里叶变换(FFT)原理及频谱分析MatLab实现

傅里叶变换在信号处理中具有十分重要的作用，但是离散时间的傅里叶变换具有很大的时间复杂度。非周期性连续时间信号x(t)的傅里叶变换可以表示为：

(1)

公式中计算出来的是信号x(t)的连续频谱。但是，在实际的控制系统中能够得到的是连续信号x(t)的离散采样值x(nT)。因此需要利用离散信号x(nT)来计算信号x(t)的频谱。有限长离散信号x(n)，n=0，1，…，N-1的DFT定义为：

(2)

这里，k=0,1,…,N-1。可以看出，DFT需要计算大约N2次乘法和N2次加法。当N较大时，这个计算量是很大的。而快速傅里叶变换(FFT)减少了DFT的运算次数,通过在时域将序列逐次分解为一组子序列，然后利用子序列的DFT来实现整个序列的DFT，从而减少了离散傅里叶变换的运算量，提高了计算效率。在MatLab中对输入信号实现快速傅里叶变换的命令如下[4]：

Xf=fft(xt,N)

(3)

其中Xt是输入信号序列，N为序列的长度，Xf是输出的信号序列，也就是Xt的频谱特征。图1是成都台JCZ-1T于2016年6月18日09时23分记录到的Unimak Island Region, Alaska地区的地震，震级M4.7，震中距67°，震源深度10 km。通过对该地震事件进行快速傅里叶(FFT)变换，得到了地震的优势频率和干扰信号的优势频率。由图1中可以看出，经过快速傅里叶(FFT)变换后得到的地震记录的频谱中，地震信号的优势频率是在0-1 Hz的区间，干扰信号的优势频率是在2～5 Hz的区间。在设计滤波器对干扰部分进行“过滤”的同时，应当对于包含地震信息的频率部分尽可能保护，这一点在设计滤波器时需要格外注意。

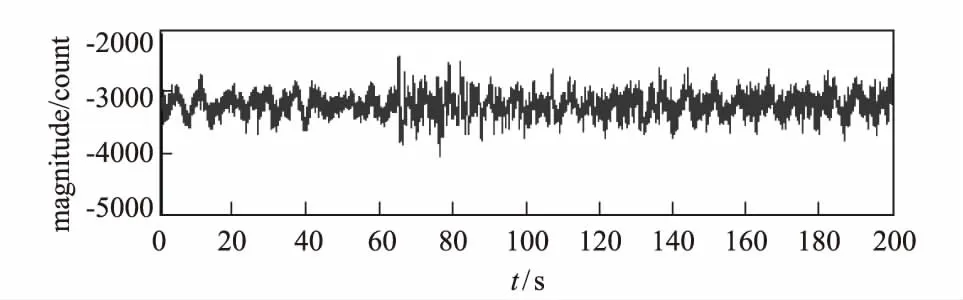
图1 地震记录的原始波形

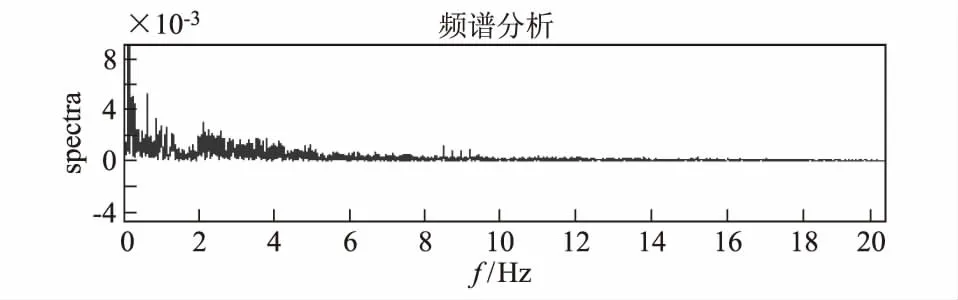
图2 地震记录的频率谱

2 FIR与IIR数字滤波器的设计

在地震分析中必须要先对原始信号进行滤波处理，滤波的目的是为了去除噪声，使原始信号通过滤波器后能够清晰地显示出优势频率。数字滤波器的主要功能是对数字信号进行处理时最常见的方法是保留数字信号中有用的频率成分，去除信号中无用的频率成分[4]。

2.1 FIR数字滤波器原理及设计

FIR滤波器的单位冲击响应h(n)是有限长(0≤n≤N-1)，其Z变换为：

(4)

在有限Z平面有(N-1)个零点，而它的(N-1)个极点均位于原点z=0处。FIR滤波器的系统差分方程为：

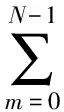
(5)

h(n)的频率响应H(ejw)可表示为：

(6)

信号通过FIR不失真条件是滤波器在通带内具有恒定的幅频特性和线性相位特性。线性相位FIR滤波器的相位滞后和群延迟在整个频带上是相等且不变的，所以，FIR滤波器虽然有相位延迟，但是通过滤波器的波形仍然保持原有形状且不会相位失真。FIR带阻滤波器的设计思路大致如下：确定带阻滤波器性能参数，如采样频率Fs，通带上、下截止频率flp,fhp,阻带下、上截止频率fls,fhs。通过“wlp=2*flp*pi/Fs”公式依次计算阻带、通带上下限归一化角频率wls,whs,whp,程序：wlp=2*flp*pi/Fs;whp=2*fhp*pi/Fs;wls=2*fls*pi/Fs;whs=2*fhs*pi/Fs(归一化角频率)。Fir1是MatLab信号处理工具箱中采用经典窗函数法设计线性FIR数字滤波器的函数，调用格式：b=fir1(N,wn,'type',window)，其中b为滤波器系数；N为滤波器阶数；wn为滤波器截止频率；‘type’为设计滤波器的类型，如带阻，type=stop，高通则type=high；window为窗函数类型。计算滤波器截止频率wn，wn=[(wlp+wls)/(2*pi),(whp+whs)/(2*pi)]。计算滤波器阶数N，程序如下:k1=wls-wlp;k2=whp-whs;kw=min(k1,k2);N=ceil(1.8*pi/kw);N=N+rem(N,2);使用窗函数;window=Boxcar(N+1);设置滤波器类型：type=stop;得到滤波器系数：b=fir1(N,wn,'stop',window);

调入地震原始数据，对地震数据进行滤波并输出滤波前后波形图。程序：

subplot(2,1,1),plot(t,a),xlabel(′t/s′),ylabel(′magnitude/count′),title(‘滤波前地震波形’),

subplot(2,1,2),plot(t,sf),xlabel(′t/s′),ylabel(′magnitude/count′),title(‘滤波后地震波形’);

512个点绘制滤波器频谱，程序：

[h1,w]=freqz(b,1,512); %使用512个点绘制滤波器幅频特性

subplot(2,1,1),plot(w*Fs/(2*pi),20*log(abs(h1)/abs(h1(1)))),xlabel('频率/ HZ′),

ylabel('幅度/dB′),title(‘FIR带阻滤波器幅频特性’)。

2.2 IIR数字滤波器原理及设计

滤波器的设计本质上是寻找一个既能物理实现，又能满足给定频率特性指标要求的系统传输函数。IIR滤波器一般采用递归型的结构，系统的输入与输出服从N阶差分方程：

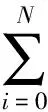
(7)

而IIR的传输函数为：

(8)

h(n)为滤波器的脉冲响应，取值范围在n∈[0,∞]。M和N为分解的分子和分母的系数个数[4]。IIR滤波器在同样的性能指标的前提下，需要的阶数明显要低于FIR滤波器。所用存储单元少，计算量小，效率更高，但其缺点是相位的非线性。根据频谱分析的结果以及干扰信号的频率区间，需要设计IIR带阻滤波器。设计思路是,利用已有的模拟滤波器设计理论，采用巴特沃斯butterworth模拟滤波器，然后再通过双线性变换法，完成从模拟到数字的变换。确定滤波器的技术指标，包括采样频率Fs，通带和阻带的上、下限归一化角频率(wlp、wls、whp、whs)，通带衰减Rp,阻带衰减Rs。通过计算求取频率预畸变以及归一化通、阻带频率，程序如下：

T=1/Fs; %采样间隔

wc1=(2/T)*tan(wlp/2);wc2=(2/T)*tan(whp/2);wr1=(2/T)*tan(wls/2);

wr2=(2/T)*tan(whs/2); %频率预畸变

w0=sqrt(wc1*wc2); R=wc2-wc1; wp=1; %归一化通带截止频率

ws=wp*(wr1*R)/(w0^2-wr1^2); %归一化阻带截止频率

用函数[N,wn]=buttord(wp,ws,Rp,Rs,'s')确定最小阶数N和频率参数Wn。再求出滤波器传输函数多项式系数向量b,a。相关程序：

[Z,P,K]=buttap(N); [MT,NT]=zp2tf(Z,P,K); %将零极点形式转换为传输形式

[M,N]=lp2bs(MT,NT,w0,R); %对低通滤波器进行频率变换，转换为带阻滤波

[b,a]=bilinear(M,N,Fs); %对模拟滤波器进行双性变换。

绘出所设计滤波器幅幅频响应。相应程序：

[H,W]=freqz(b,a); subplot(2,1,1),plot(W*Fs/(2*pi),abs(H)),xlabel(‘频率’),ylabel(‘幅值’),title(‘IIR带阻滤波器幅频响应’); %绘出滤波器幅频响应。调入地震原始数据，对地震数据进行滤波并输出滤波前后波形图。程序如下：

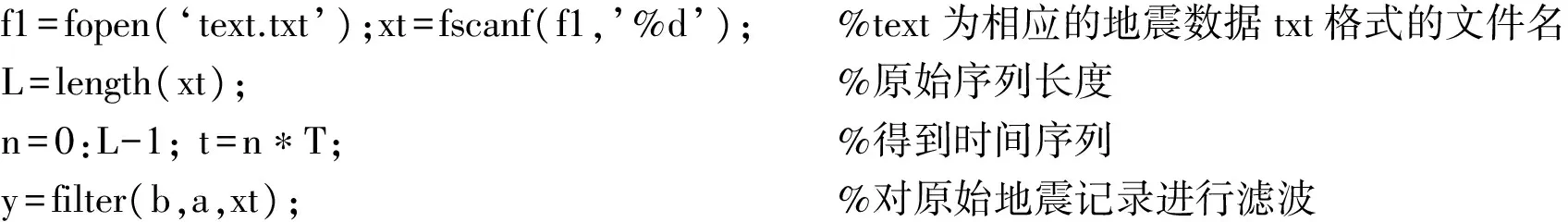
subplot(2,1,1),plot(t,xt),xlabel(′t/s′),ylabel(′magnitude/count′),title(‘滤波前地震波形’),

subplot(2,1,2),plot(t,y),xlabel(′t/s′),ylabel(′magnitude/count′),title(‘滤波后地震波形’)。

3 对地震数据滤波处理实例

由于成都台记录到的中小震级远震受到干扰明显，以图1的4.7级远震为例，通过频谱分析(参见图2)，确定地震的优势频率在0～1.5 Hz，干扰的优势频率为2～85 Hz，因此设计了FIR带阻滤波器与IIR带阻滤波器分别处理。为了尽可能的保留有用的地震信息频率，对两种滤波器做如下参数设置：FIR带阻滤波器：采样频率Fs=100 Hz;通带上截止频率flp=2 Hz;通带下截止频率fhp=5.5 Hz;阻带下截止频率fls=2.1 Hz;阻带上截止频率fhs=5 Hz;IIR带阻滤波器：采样频率Fs=100 Hz;通带上截止归一化角频率wlp=0.04*pi;通带下截止归一化角频率whp=0.11*pi;阻带下截止归一化角频率wls=0.042*pi;阻带上截止归一化角频率whs=0.10*pi;通带衰减Rp=1 dB;阻带衰减Rs=3 dB;经过程序运行后，得到滤波器的幅频特性(参见图3)，在频谱上可以看到干扰的频率被过滤掉(参见图4)，波形也得到明显的改善(参见图5～6)。由图4可以知，FIR、IIR滤波器应用效果明显，2～5 Hz的干扰被最大程度过滤，保留了地震信息的优势频率。在图5和图6中可以看出，滤波前的原始地震波形记录“毛刺”较多，波形受干扰严重，P波的初动方向无法清楚辨别。经过滤波器滤波后，地震记录改善十分明显，之前的“毛刺”大大减少，波形更加清楚，P波的初动方向可以清晰辨认。FIR与IIR两种滤波器都取的了很好的效果，但对比图5和图6可以发现，图5中地震的初动在时间上相对于原始波形稍有滞后，这是由于FIR滤波器的相位滞后造成的，但波形仍然保持原有形状且相位无失真。在成都台地震记录中，除了中小震级的远震，近震和地方震波形都受到很大程度的干扰，甚至混夹干扰信号难以分辨。因此，本文对近震进行了处理与分析，以2016年07月27日19时59分记录于JCZ-1T的四川平武ML2.5级地震为例。首先通过对四川平武ML2.5级地震谱分析(参见图7)，确定地震信号的优势频率是在0～0.5 Hz，属于0～1 Hz的区间；干扰的优势频率在2～4 Hz的区间。因此，需要设计符合要求的带阻滤波器去除干扰。改变技术参数使得：flp=2;fls=2.1;fhs=4;fhp=5;wlp=0.04*pi;wls=0.042*pi;whs=0.08*pi;whp=0.10*pi;运行程序后得到图8。

图3 FIR滤波幅频特性及IIR滤波器幅频响应

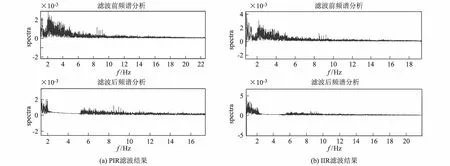
左为FIR滤波结果；右为IIR滤波结果图4 滤波前后的频率谱

图5 FIR滤波器滤波后的地震波形

图6 IIR滤波器滤波后的地震波形

图7 四川平武ML2.5级地震记录的频率谱

(图左 FIR滤波结果 图右IIR滤波结果)图8 滤波前后的频率谱图

由图8可以看出2～4 Hz的干扰频率已经被很大程度过滤掉了。图9、图10可知，FIR滤波器和IIR滤波器应用效果均明显，地震波形记录经过滤波器处理后，干扰的频率被过滤，而地震信息的频率得到了尽可能的保留。经过滤波器处理后的地震波形记录相较于原始地震记录有了明显的改善，干扰“毛刺”大大的减少，原始地震波形记录中被淹没的近震的波形也更加清晰。FIR滤波器滤波后的波形相位稍有滞后，但波形仍然保持原有形状且相位无失真。

图9 FIR滤波器滤波后的地震波形

图10 IIR滤波器滤波后的地震波形

4 讨论

根据文中列举的记录于JCZ-1T的地震实例的频谱，可以发现干扰频率都包含在2～4 Hz的区间。为了证实干扰是来自外界环境还是JCZ-1T仪器本身，本文截取了2016年02月19日21点19分记录于JCZ-1的地震波形数据来作为对比研究。通过对数据进行频谱分析，发现仍然存在2-4 Hz的区间干扰(参见图11)，并设计了相应的IIR带阻滤波器进行处理，从处理结果(参见图12)来看，波形有了明显改善，干扰明显减少。为了减小结果的偶然性，本文另截取了2016年06月18日19点51分记录于JCZ-1T的地震波形数据作为比较。以得出的频率谱(参见图13)以及IIR带阻滤波器处理前后的地震波形记录(参见图14)，证实了来自于外界环境2-4 Hz的干扰信息是造成成都台地震波形记录不佳的重要因素。

图11 记录于JCZ-1的地震记录频率谱

图12 IIR滤波器滤波前后记录于JCZ-1的地震记录

图13 记录于JCZ-1T的地震记录频率谱

图14 IIR滤波器滤波前后记录于JCZ-1T的地震记录

处理实例都是通过MatLab程序代码来实现的，针对不同实例的频谱对滤波器的相关参数做了改变，以达到过滤干扰和提高观测资料质量的目的。通过对成都地震台测震数据的处理结果来看，收效甚好，确确实实改善了原来的数据质量，通过研究过程中可总结出以下认识：来自于外界环境2～4 Hz的干扰信息是造成成都台地震波形记录不佳的重要因素，通过设计带阻数字滤波器可以去除干扰。FIR滤波器、IIR滤波器应用于成都台地震记录，均能达到理想的滤波效果，滤除了2～4 Hz频率区间的干扰，大大减小了地震波形记录中的干扰信息，改善了数据的质量，对成都地震台中小震级地震的观测记录有了很大的帮助。FIR滤波器虽然有相位延迟，但是通过滤波器的波形仍然保持原有形状且不会相位失真，并且相位线性，即不同频率分量的信号通过FIR滤波器后时间差不变；IIR滤波器在相同性能指标的前提下，相较于FIR滤波器所需阶数更少，计算量更小，效率更高，幅频特性精度更高，但相位非线性。在通过MatLab的滤波器方法对干扰信息进行排除时，应首先对干扰信息与背景噪声的分析，明确需要设计的滤波器类型，根据实际需要选取通带或者阻带的边界频率，并且尽可能保留原始观测信息。

[1] 田文德，叶建庆，胡俊明.成都地震台JCZ-1与JCZ-1T甚宽频带地震仪对比观测分析[J].地震研究，2013，3(36):372-378.

[2] 曾庆堂，起卫罗，马志刚，等.MatLab消除腾冲台数字地震记录中干扰波的应用[J].华南地震，2014，1(34).

[3] 谭雨文，刘国明.MatLab在地震信号处理中的应用实例[J].防灾减灾学报，2011，3(27).

[4] 万永革. MatLab数字信号处理实例教程[M].北京：科学出版社，2012.

ApplicationandResearchofMatLabintheDigitalSeismicRecordsatChengduSeismicStandardStation

HE Siyuan, LIU Huajiao, XU Wenhai, ZHONG Libin, DONG Lijie

(Chengdu Seismic Standard Station, Sichuan Earthquake Agency, Sichuan Chengdu 611730, China)

In Chengdu Seismic Standard Station,the seismic data of the middle and small magnitude events contain more serious interference.In this paper,the software MatLab is used to process the digital seismic records in order to reduce the interference.Two software FIR and IIR filters in the MatLab are two types of wave interference filters.The results processed by these two filters are good.It is found that the interference with the frequency 2～4 Hz is an important cause of poor-quality.That is valuable for the work about analysis and processing of seismic data in the future.

MatLab；digital seismic records；interference wave；filter

2016-09-21

何思源(1991-)，男，四川省安岳县人，助理工程师，主要从事测震分析.

P315.69

B

1001-8115(2017)04-0005-07

10.13716/j.cnki.1001-8115.2017.04.002