跨坐式单轨车辆走行轮轮辋优化设计*

杜子学 杨 震 许舟洲 侯忠伟 王湘寿

（1.重庆交通大学交通运输学院，400074，重庆；2.通号轨道车辆有限公司，410100，长沙//第一作者，教授）

跨坐式单轨车辆走行轮轮辋优化设计*

杜子学1杨 震1许舟洲1侯忠伟1王湘寿2

（1.重庆交通大学交通运输学院，400074，重庆；2.通号轨道车辆有限公司，410100，长沙//第一作者，教授）

跨坐式单轨车辆的转向架结构与其他轨道交通车辆不同，其转向架走行机理差异是关键。为此，从单轨列车轮辋与轮芯的摩擦连接行为、摩擦特性研究入手，将走行轮轮辋圆锥斜面椎角由28°优化为27°。通过静扭试验，验证了优化后的27°轮辋传动性能优于28°轮辋。运用Hyperwoks有限元软件计算分析，结果表明优化过后的轮辋刚度与强度均满足设计要求。

跨坐式单轨车辆；走行轮；轮辋；优化设计

跨坐式单轨交通车辆的转向架结构及轨道梁形式与其他轨道交通车辆不同，故跨坐式单轨车辆的走行轮必然是小直径、大负荷能力的橡胶轮胎，而与轮胎相配合的轮辋与轮芯也必然是全新设计的非标准件。由于转向架空间紧凑，走行轮轮辋与轮芯采用楔块锁紧的圆锥面无键联接，因此，实现轮辋-轮芯驱动系统的稳定性是跨坐式单轨车辆走行系统技术的关键。

无圆锥面无键联接具有对中性好、联接零件无键槽削弱、传递转矩大等特点，在正反转及较大冲击载荷工况下也能可靠工作,可多次装拆而不易损伤配合表面,具有一定的过载保护功能［1］。在跨坐式单轨走行系统轮辋圆锥面无键连接中，准确分析锥角与传递扭矩的关系对增加传动系统安全系数、保障车辆运行安全具有重要意义。

1 跨坐式单轨车辆走行系统的结构和原理

单轨列车走行系统主要由驱动轴、轮芯、内外轮辋、锁环、挡圈、隔圈、轮胎和楔块等零部件组成（如图1所示）。单轨列车走行系统与汽车行驶系统的驱动桥类似，但减速器的布置方式与汽车不同。减速箱输出的扭矩通过驱动轴传递给轮芯；楔块以双头螺柱固定在轮芯上，通过圆锥面过盈联接产生的摩擦将动力传递给轮辋，从而实现动力传输。在单轨列车走行系统的轮辋-轮芯系统中充分利用了摩擦原理，楔块起到了关键的“桥梁”作用［2］。

根据重庆跨坐式单轨车辆相关资料，进口车体轮辋体与楔块及轮芯的配合锥度角为28°（如图2所示）。本文选取27°为优化的配合锥度角，并对二者进行对比分析。

2 配合锥度角优化前后的对比分析

参考圆锥面无键联接的受力计算分析［3-4］，对轮辋轮芯系统的楔块进行受力分析（见图3）。

在图3中两个斜面所受压力F1、F2，可由楔块的静力平衡方程方程求出：

图1 走行系统的结构图

图2 锥角为28°的楔块

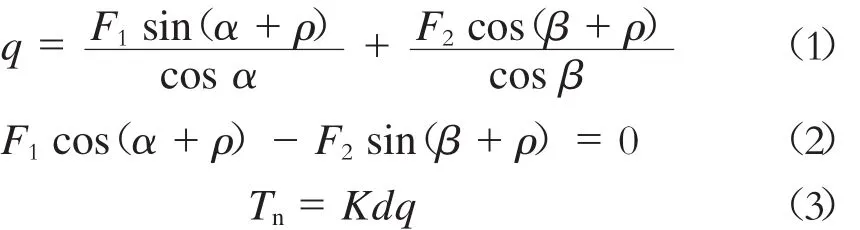
式中：

q——螺栓预紧力；

K——与摩擦有关的系数，一般K=0.2；

Tn——螺栓拧紧力矩；

d——连接螺栓的直径；

α——楔块与轮辋配合的锥面斜角；

β——楔块与轮芯配合的斜面锥角；

ρ——摩擦角，ρ=arctan（f）；

f——楔块与轮辋轮芯的摩擦系数，当钢件与钢件之间没有摩擦时f=0.15。

当楔块锁紧螺母的拧紧力矩Tn=170 Nm时，如α=28°，则 F1，28°=58 801.110 N，F2，28°=48 628.518 N；如 α=27°，则 F1，27°=60 471.591 N，F2，27°=53 215.000 N。

每个轮辋-轮芯系统有12个楔块，所以每个轮辋-轮芯系统由楔块在整个轮辋配合面上传递的总压力为：

图3 楔块受力图

在配合面上传递的摩擦力为F磨=F1，总f，则有：

轮辋轮芯系统能提供的最大扭矩Tmax=F磨d/2。

其中，28°轮辋平均结合直径 d1=374.7 mm，27°轮辋平均结合直径d2=373.7 mm。

由计算所得，在相同的楔块螺母锁紧力下，27°轮辋能传递的最大扭矩大于28°轮辋。故选择27°轮辋。楔块与轮辋体配合的斜面锥角相应为27°。27°楔块与28°楔块如图4～5所示。

结合图4～5，计算可得当楔块与轮辋配合的斜面椎角改为27°后，楔块与轮辋配合的长度由13.69 mm增加到17.03 mm；相应的楔块与轮辋体配合的面积Aα也会增加（如图6所示）。

28°楔块与轮辋的配合面面积为 A28°=708.81 mm，27°楔块与轮辋的配合面面积为 A27°=978.94 mm。楔块与轮辋配合面的接触压应力为：

式中：

Fα——楔块与轮辋接触面的压力。

经计算，P28°=82.96 MPa，P27°=61.77 MPa。可见，28°楔块对轮辋体的应力较大。

因此，改进后的27°轮辋-轮芯系统不仅能传递更大的扭矩，而且27°楔块对轮辋体的应力更小。

经过严格的设计计算，将跨坐式单轨车辆走行系统的轮辋-轮芯系统中轮辋锥角以及与轮辋配合的楔块的锥角优化为27°。

图4 斜面椎角为28°的楔块

3.3 试验结果

试验结果见表1。

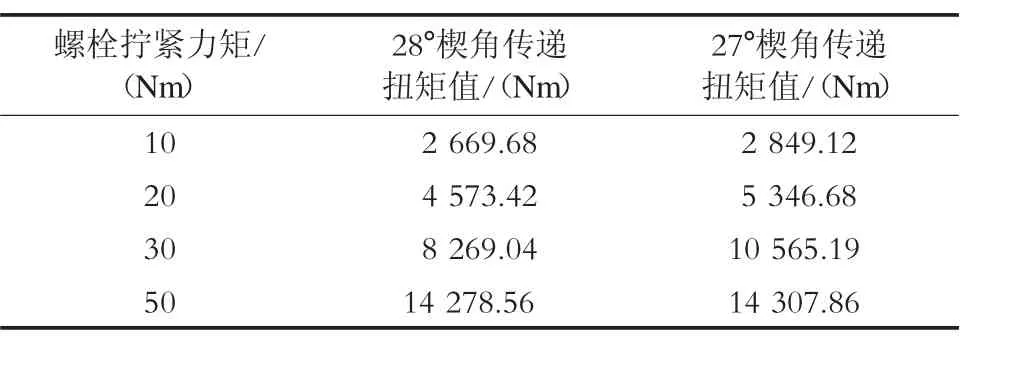
表1 试验结果

图5 斜面椎角为27°的楔块

图 6 28°楔块与27°楔块实景

3 轮辋-轮芯系统的承载能力试验

3.1 试验轮辋的设计

跨坐式单轨车辆的轮辋与轮芯因结构原因，无法安装在静扭试验台上，故重新设计制造了便于与静扭试验台安装的28°、27°模拟轮辋及轮芯。模拟轮辋轮芯的配合尺寸，材质与加工工艺均按照原件图纸。

3.2 试验方案

在静扭试验台上，对27°、28°两种锥度角的轮辋-轮芯-楔块系统的楔块螺栓分别施加10 Nm、20 Nm、30 Nm、50 Nm的扭矩，并依次以10 Nm递增，从而测试出在楔块螺栓不同拧紧力矩下能传递的最大扭矩。

如发生打滑，或者模拟组件能传递的最大力矩接近 T1=Tηn=14 405．09 Nm 时，则停止试验，认为达到了极端状况。如继续增加楔块螺栓预紧力，然后加载使模拟组件打滑，则可能损坏组件，或者超出连接螺栓能够承受的极限，会带来危险性后果。

从试验结果可以看出，27°轮辋-轮芯系统能传递的最大扭矩都大于28°轮辋-轮芯系统，证明了改进后的27°锥角的轮辋传动性能优于28°轮辋。

4 轮辋有限元分析

对外轮辋进行静载荷、动载荷及紧急制动等3种工况下的有限元分析。外轮辋在各工况下的应力应变分析结果见表2。

表2 外轮辋各工况下应力应变有限元分析结果

根据计算分析结果，在各种工况下的外轮辋较大变形均主要集中在轮辋外轮缘处（见图7），最大变形量为0.178 mm。此变形量相对较小，安全系数足够，轮辋刚度满足设计要求。

图7 外轮辋最大变形处

根据计算分析结果，各种工况下外轮辋的较大应力主要集中在楔块与轮辋接触面（见图8）。最大应力为168.1 MPa，远小于轮辋材料的屈服强度，具有足够的安全系数。轮辋强度满足设计要求。

图8 外轮辋最大应力处

5 结语

通过静扭试验，优化后的轮辋-轮芯系统在承载能力上优于优化前，而且通过有限元分析计算，优化后的轮辋强度与刚度都满足设计要求，优化后的轮辋-轮芯走行系统对增加传动系统安全系数和车辆运行安全具有重要意义。本文对跨坐式单轨轮辋-轮芯进行优化分析及试验，这对跨坐式单轨车辆轮辋的国产化以及圆锥面无键联接在城市轨道交通中的应用具有指导意义。圆锥面无键联接属于过盈联接，在联接面上由于楔块的锁紧，楔块与轮辋接触面上由于过盈产生的过盈力对轮辋强度产生的影响，还需要作进一步研究。

［1］ 李海国，张小菊，徐庆杰.几种无键联接机构的形式及特点［J］.重型机械科技，2007（4）：46.

［2］ 颜溯，杜子学，何希和.跨座式单轨交通车辆道岔结构及分析［M］.北京：人民交通出版社，2013：12.

［3］ 刘万俊，王志坚，龚小平，等.一种新的无键联接结构设计［J］.现代机械，2005（2）：44.

［4］ 韩正铜.圆锥面无键联接的受力分析计算［J］.机械科学与技术，1995（3）：13.

Structural Optimization of Walking Wheel Rim Design for Straddle-type Monorail Vehicle

DU Zixue，YANG Zhen，XU Zhouzhou，HOU Zhongwei，WANG Xiangtao

The important difference between straddle-type monorail and the subway system is the bogie structure,the key discrepancy of which is the bogie direction mechanism.Therefore,the optimization of walking wheel is studied firstly from the perspective of the friction and connection behavior between the wheel rim and wheel core,the conical surface angle of walking wheel rim is optimized from 28 degrees to 27.Through static torsion test,the 27 degrees rim has displayed higher drive performance than the 28 degrees rim.Then the finite element analysis software Hyperwoks is used to analyze the straddle-type monorail rim,and the results indicate that the optimized stiffness and strength of the walking wheel rim can meet the design requirements.

straddle-type monorail vehicle；walking wheel；rim；optimum design

First-author′s address Traffic and Transportation College，Chongqing Jiaotong University，400074，Chongqing，China

U270.33∶U232

10.16037/j.1007-869x.2017.12.006

*国家自然科学基金项目（51475062）

2016-04-14）