GO/AP法角反射器可变RCS模拟技术*

郝炎祯，诸德放，陈朋，高松

(1.空军勤务学院 航空弹药系，江苏 徐州 221000；2.中国人民解放军94592部队，江苏 徐州 221000)

0 引言

目前，大部分靶机使用的雷达散射特性模拟技术都为固定雷达散射截面积的模拟技术，其虽可满足雷达型空空导弹、地/舰空导弹等武器的训练打靶需求，但因无法调整模拟目标RCS值的大小，只能模拟特定飞行目标的雷达散射特性，导致其使用局限性很大。为了提高靶机功能覆盖，发展可变雷达散射特性模拟技术很有必要。固定RCS技术包括：介质反射器、角反射器以及龙伯透镜反射器3种主流技术[1]。其中龙伯透镜发射器体积小、结构复杂、造价高[2]；介质反射器因材质和工艺水平要求较高，价格相对较高；而角反射器材质为普通金属，工艺水平要求低，界面刚度较大，价格低廉且能满足供靶需求[3]，因此为降低成本、提高打靶效费比选用角反射器作为模拟雷达散射特性的基础装置进行研究。

GO/AP法是一种综合利用几何光学和区域投影进行电大尺寸目标单站雷达散射截面积预估的高频混合算法。本文根据GO/AP法对三面角反射器雷达散射面积进行分析，得出旋转角反射器部分侧面实现可变RCS模拟的结论，在此基础上设计了角反射器可变RCS装置，并利用FEKO电磁仿真软件验证了角反射器可变RCS技术。

1 角反射器可变RCS原理分析

角反射器通常有二面、三面及多面的，常见的为四面体锥状，由3个两两互相垂直的金属反射直角面的立体结构，该结构能够将不同方向入射的雷达波按原方向反射回去[4]。当有雷达电磁波沿AB入射时，经相互垂直的M1与M22块平面金属板反射后，沿CD方向即沿AB的相反方向反射出去[5]，如图1所示。扩展到三维空间上可知沿任意方向射向角反射器的雷达电磁波均可经2次或最多3次反射最终将沿原来的入射方向的相反方向反射出去，其雷达散射截面积由这3次在角反射器内部的反射形成的雷达散射截面叠加而成。因此，能够模拟比自身大得多的物体的雷达反射信号，具有很大的雷达散射截面积。

图1 电磁波镜面反射示意图Fig.1 Schematic diagram of electromagnetic wave specular reflection

三面角反射器垂直边通常为dm级，对工作在cm波段的雷达来说可视为是“电大尺寸目标”。目前，在计算“电大目标”的RCS值时有多种方法。例如：射线弹跳(SBR)法[6]、高斯光束(GB)法[7]和复射线(CR)法[8]，这3种方法对射线密度要求很高且计算量大，有较大局限性。物理光学(PO)法[9-10]进行RCS预估时需分别考虑1～3次的散射贡献，计算过程复杂。GO/AP法是一种直观的RCS预估方法，其计算过程简便，运算量小，本文选用GO/AP法作为角反射器RCS的预估方法。

建立三面角反射器坐标系，以O点为空间坐标原点，设角反射器棱边长L，即A点坐标为(L，0，0)，B点为(0，L，0)，C点为(0，0，L)。入射电磁波入射方向为n(k，m，n)=(cosα，cosβ，cosγ)=(cosα=sinθcosφ，cosβ=sinθsinφ，cosγ=cosθ)，其中θ为入射电磁波与Oz轴的夹角，φ为入射电磁波在Oxy平面的投影与Ox的夹角，角反射器空间模型如图2所示。

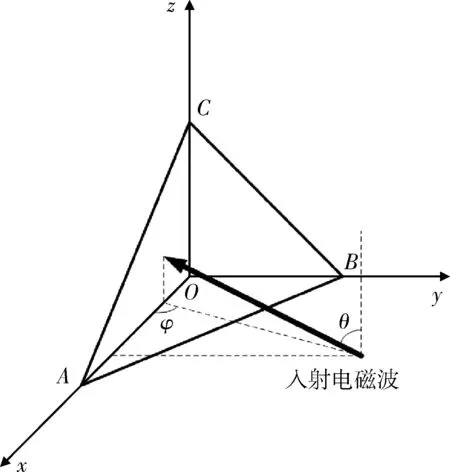
图2 角反射器空间模型Fig.2 Angle reflector space model

用GO/AP法预估RCS时，可以将角反射体等效为过顶点垂直于入射方向的某一特定大小的平面，该平面称为“等效平面”，其面积称为“有效反射面积”，记作Aeq。这样就可以利用波长λ的平面波垂直入射平板时的RCS公式预估角反射体的RCS。即

(1)

由于入射电磁波长λ可设为定值，因此，只需要确定等效平面的形状并积分求得有效反射面积Aeq，便可求得角反射体的RCS。Aeq可通过区域投影确定：将角反射体投影到过顶点O垂直于入射方向的平面上，所得投影称为“实孔径”；在投影面上，将“实孔径”绕顶点O旋转180°，得到“虚孔径”；实、虚孔径的重合区域即为Aeq[11]。

为求得角反射器等效面积Aeq，需建立虚实孔径所在空间的坐标系，设实孔径三角形为A′B′C′，虚孔径三角形为A″B″C″，实孔径所在空间坐标系仍以O点为原点，Ox′轴是沿OA′方向延伸，Oy′轴是沿OB′方向延伸，Oz′轴是沿OC′方向延伸。 三面角反射器的Aeq通常为平行四边形、六边形，当方位角φ=30°，俯仰角θ=15°时角反射器等效面积Aeq如图3所示。

图3 角反射器等效面积示意图Fig.3 Schematic diagram of equivalent area of corner reflector

因等效面积Aeq所在的等效平面位于O′x′y′z′，故需将Oxyz的坐标变换到O′x′y′z′，变换矩阵为

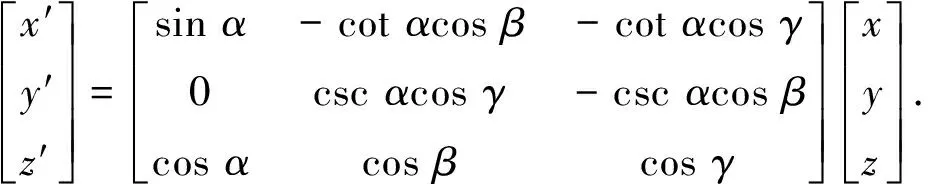
(2)

通过式(2)求得点A′,B′,C′,A″,B″,C″在O′x′y′z′坐标系上的坐标，进而求得等效多边形边界线的方程：

(3)

根据边界方程可知，当入射电磁波的方位角和俯仰角变换时，等效多边形的形状会发生变化，根据实(虚)孔径的顶点与虚(实)孔径中相对边线的重合关系，以顶点位于相应边线为临界点，可将入射方向以曲线A,B为界划分成3个区域，如图4所示，区域1,3中的有效反射面积为平行四边形，区域2中为六边形[11]。

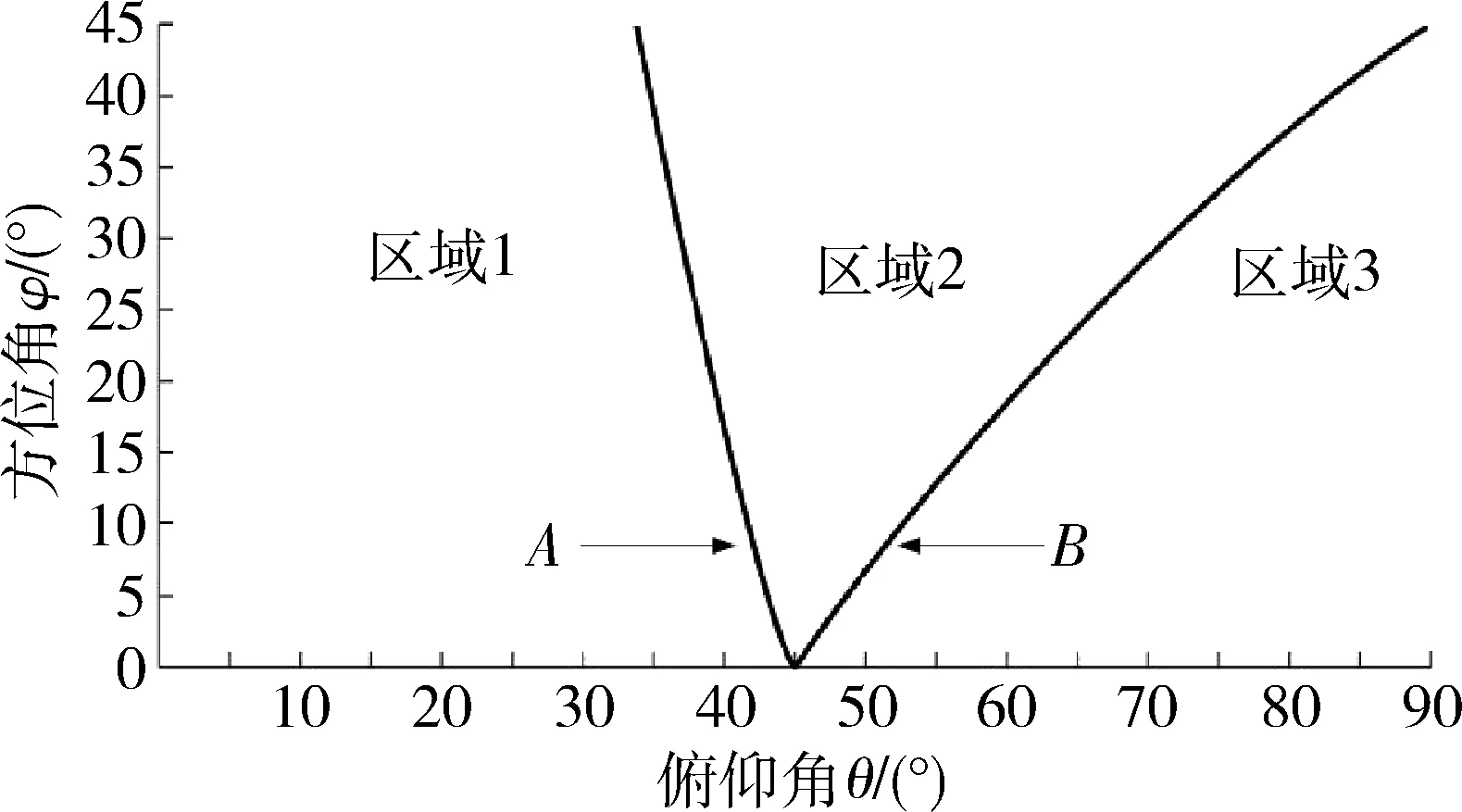
图4 三面角反射体的入射方向分区Fig.4 Incidence direction of the triangular reflector

其中曲线A和曲线B的方程为

(4)

由式(3)和式(4)得出等效面积Aeq的公式为

(5)

角反射器RCS值可变原理：由式(1)与式(5)可得计算角反射器的RCS的公式，从式中可知当电磁波入射的俯仰角与方位角变化时，将直接影响角反射器的RCS值。基于此当固定电磁波入射角以及角反射器底面C，同时以斜边OA,OB为轴旋转角反射器的侧面A和侧面B，将会改变任意方向射来的电磁波入射方位角和俯仰角的大小，进而改变角反射器的等效面积Aeq的大小，最终实现角反射器RCS值可变的目的。

2 角反射器可变RCS装置设计

根据角反射器RCS值可变原理，选择三面角反射器，将底面C固定，侧面A和侧面B进行旋转，侧面A沿斜边OA旋转，侧面B沿斜边OB旋转。因角反射器是轴对称物体，为使获得模拟出的RCS曲线与未旋转状态相同，两侧面旋转角度大小应保持一致。

为实现侧面旋转需设置相应的硬件设备，包括三面角反射器、电源、控制器、电动机以及连杆装置。其中三面角反射器两侧面斜边与底面固定，根据不同旋转方案在角反射器2侧面设置不同连杆装置连接点，由控制器驱动电动机带动连杆装置运动，进而实现控制角反射器两侧面旋转的目的。为节省经费，侧面旋转也可手动完成，只需设置相应旋转角度金属侧面的固定装置即可。

3 基于FEKO的角反射器可变RCS仿真校验

当前，对于电大目标的RCS仿真主要采用FEKO及CST 2款电磁场高频计算软件，其中FEKO的算法较多，有矩量法(MOM)、物理光学法(PO)、以及快速多极子求解方法(MLFMM)等。针对角反射器自身特性以及仿真计算机处理器性能选择FEKO的快速多极子求解方法(MLFMM)进行仿真计算。

3.1 仿真参数设置

建立三面角反射器，材质选择为角反射器常用铝合金材质，厚度为1 mm；激励源选择为波长3 cm，频率为国内外通用的警戒和远距离探测频率10 GHz的平面波，方位角为0，俯仰角为45°；远场设置为方位角0，俯仰角0°～90°，步长为1；为节省计算机内存，加快计算速度，网格划分设为0.5，该精度满足计算要求；算法选择为快速多极子求解方法(MLFMM)，为集中模型起始点设为波长的整数倍(0.3)[12-15]。角反射器仿真模型如图5所示。

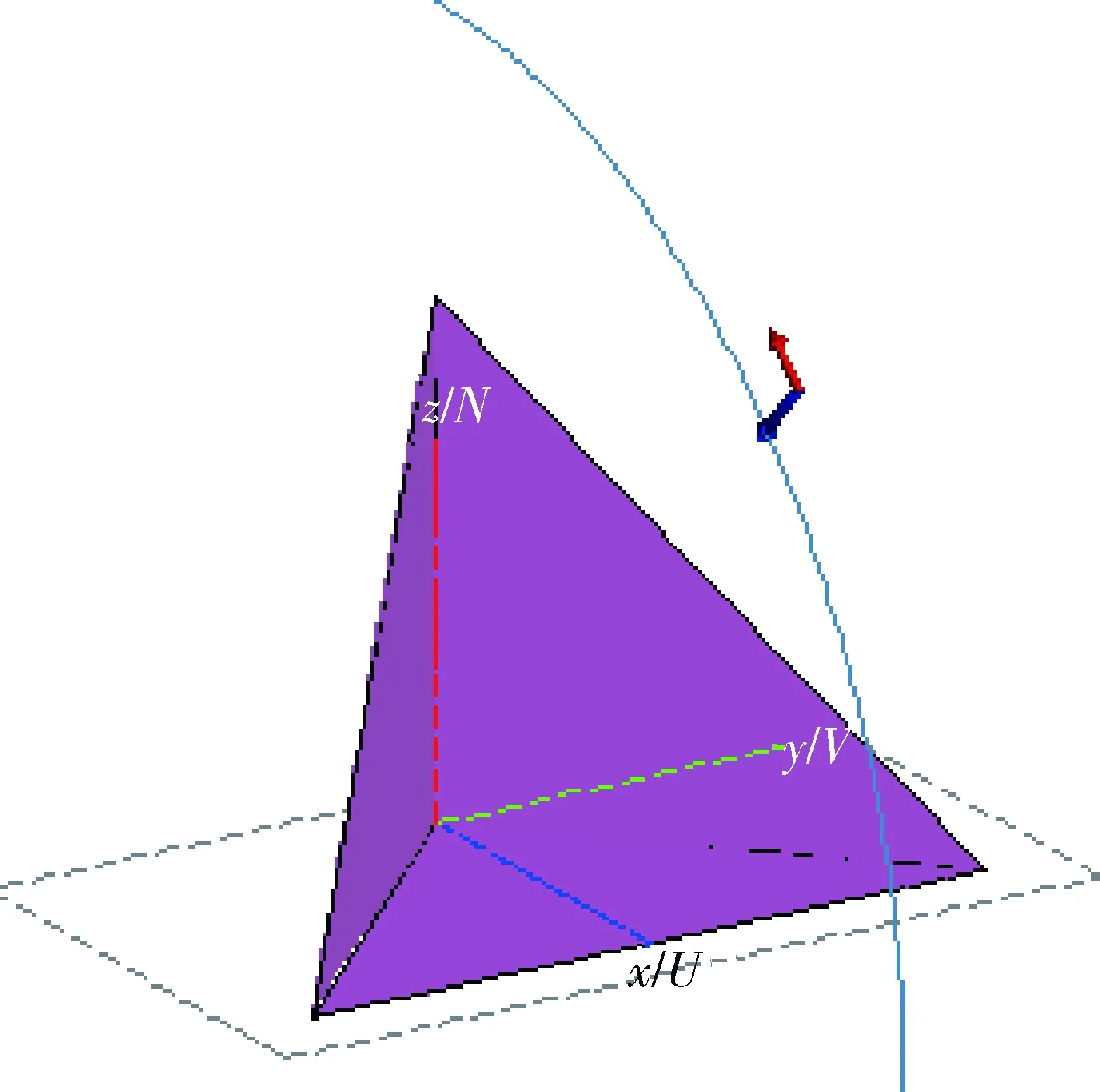
图5 角反射器仿真模型Fig.5 Corner reflector simulation model

3.2 角反射器尺寸的选择

目前，各类飞机的正向探测RCS值大约在-5～20 dBm2范围内，为模拟20 dBm2最大的RCS值，需要改变角反射器尺寸来仿真验证，具体需改变角反射器的直角边长度。分别建立20,30,40,50,60 cm 5种尺寸的仿真模型，按照上述设置进行仿真，其对应RCS值如图6所示。

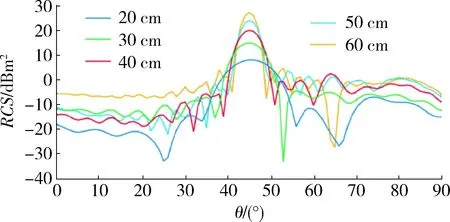
图6 多种尺寸角反射器RCS值对比图Fig.6 Comparison of RCS values of various sizes of corner reflectors

从图6中可知，当角反射器直角边为40,50,60 cm时，其最大RCS值分别为20,24,27 dBm2，而其他尺寸的角反射器最大RCS值都达不到20 dBm2要求，因靶机上空间较小，应尽量选择尺寸较小且满足模拟要求的角反射器，故选择40 cm直角边长的角反射器作为标准尺寸进行雷达散射仿真模拟。

3.3 角反射器侧面旋转方式及旋转角度选择

角反射器侧面旋转有2种方式：同向旋转和逆向旋转。同向旋转是指角反射器两侧面同时向外侧旋转相同角度，如图7所示。逆向旋转指角反射器两侧面分别向相反的方向旋转相同角度，可规定侧面A逆时针旋转，侧面B顺时针旋转，如图8所示。

图7 双外旋同向旋转Fig.7 Double external rotation

图8 逆向旋转Fig.8 Reverse rotation

旋转角度的大小直接影响RCS值的变化趋势。旋转角度越大，雷达电磁波的方位角与俯仰角变化越大，导致在角反射器内产生的3次反射数量变化，影响等效面积的大小，反之亦然。

一方面为验证2种旋转方式的RCS值变化趋势与原始状态角反射器的RCS值变化趋势相似程度;另一方面为验证旋转多种角度下的RCS值曲线与原始状态角反射器的RCS值曲线相似程度，同时选择40 cm直角边长的角反射器，分别采用双外旋和逆向旋转两种方式、多旋转角度(5°,10°,15°,30°,45°)进行验证，仿真结果如图9～13所示。

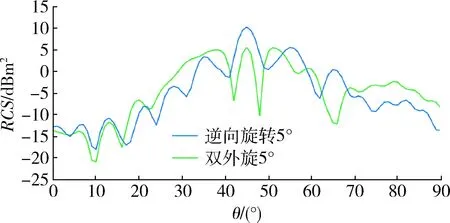
图9 旋转5°对比图Fig.9 Rotated 5° contrast map

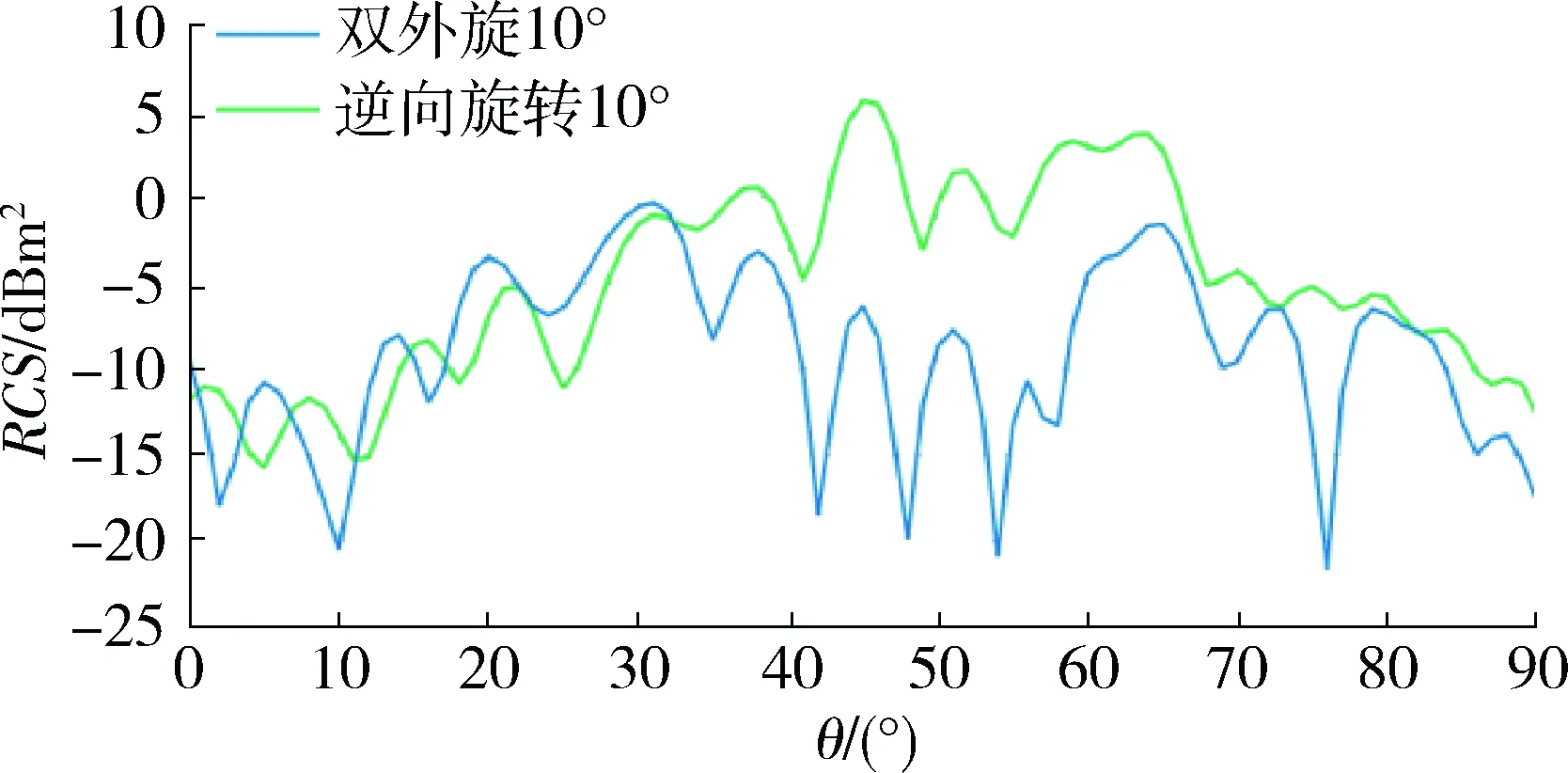
图10 旋转10°对比图Fig.10 Rotated 10° contrast map

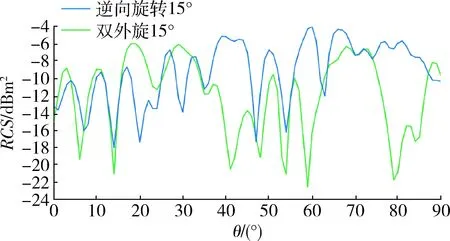
图11 旋转15°对比图Fig.11 Rotated 15°contrast map

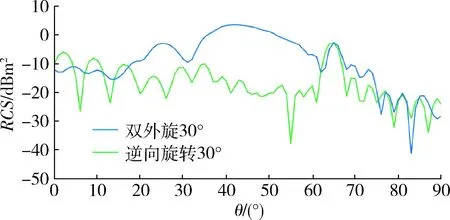
图12 旋转30°对比图Fig.12 Rotated 30°contrast map

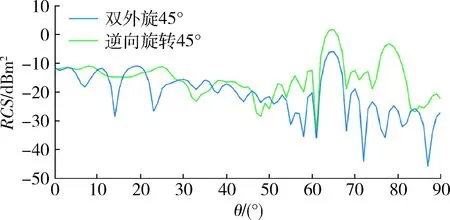
图13 旋转45°对比图 Fig.13 Rotated 45° contrast map

从图9～13中可看出，在小角度范围内(5°～15°)采用逆向旋转方式的RCS值曲线相比采用双外旋方式的RCS值曲线与原始状态角反射器的RCS值曲线重合度较高，在大角度范围(15°～45°)2种旋转方式得出的RCS曲线与原始状态角反射器的RCS值曲线重合度较低，因此，为使模拟目标雷达散射特性更为真实，角反射器侧面旋转方式应选择小角度逆向旋转方式。

3.4 角反射器可变RCS实现

为模拟更多RCS值，采用3种旋转方案。方案1：侧面A和侧面B整体旋转。方案2：2个侧面由固定不转的梯形及沿斜边旋转等腰直角三角形及构成，等腰直角三角形面积占侧面的2/3。方案3：侧面布局同方案2，但等腰直角三角形面积占侧面的一半。如图所示。角反射器尺寸选择为直角边长40 cm，侧面旋转方式选择逆向旋转，根据对称性原则旋转角度设为5°,10°,15° 3个角度对上述3个方案进行仿真。图14～16为3种方案对应不同旋转角度的RCS值曲线。

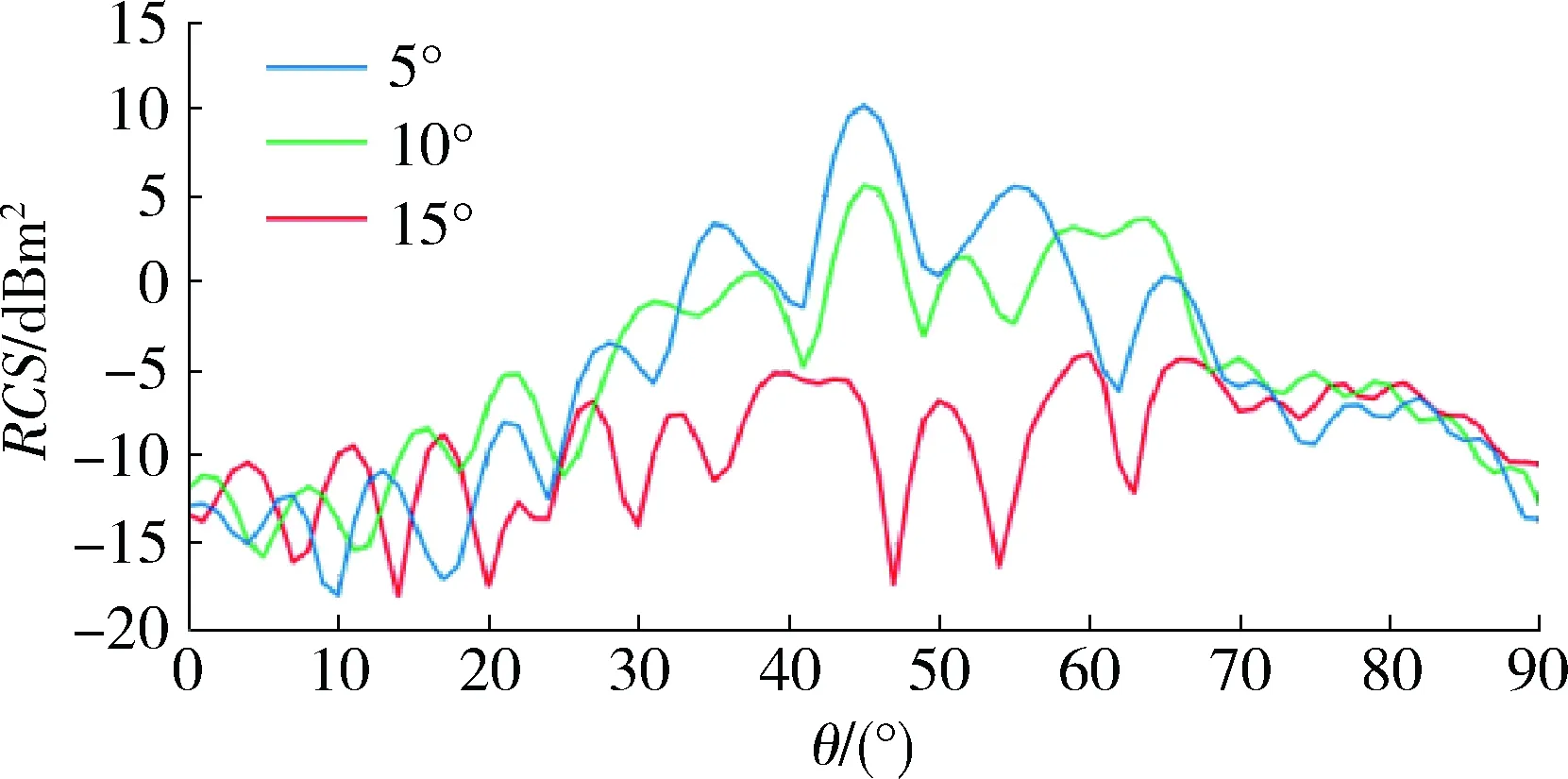
图14 整体旋转不同角度对比图Fig.14 Contrast map of the whole rotation different angles

图15 2/3旋转不同角度对比图Fig.15 Comparison chart of 2/3 rotation of different angles

图16 1/2旋转不同角度对比图Fig.16 Comparison chart of 1/2 rotation of different angles

从上述结果可看出，3种旋转方案在不同角度的RCS值基本上覆盖了飞机雷达辐射截面积-5～20 dBm2区间，说明角反射器可变RCS满足模拟不同类型飞机正向雷达辐射截面积。具体模拟情况为：方案1中旋转15°可模拟RCS值为-5 dBm2左右的各类隐身目标，例如：F-22猛禽隐身战斗机；旋转10°可模拟RCS值为5 dBm2左右的各类小型目标，例如：各型三代战斗机；旋转5°可模拟10 dBm2左右的各类小型目标，例如：各型二代战斗机。方案2中角反射器旋转5°可模拟RCS为15 dBm2左右的各类中型目标，例如：各种轻型运输机；方案3中角反射器旋转5°可模拟RCS为18 dBm2区间内的中型目标，例如：各种重型运输机及特种飞机；角反射器原始状态时可模拟RCS为20 dBm2左右的大型目标，例如：各型轰炸机。

4 结束语

本文根据GO/AP法对三面角反射器雷达散射面积进行分析，得出改变角反射器部分结构实现可变RCS模拟，在此基础上设计了角反射器可变RCS装置，并利用FEKO电磁仿真软件验证了角反射器可变RCS技术，该技术角反射器采用小角度(5°～15°)逆向旋转方式可实现-5～20 dBm2空中目标的雷达辐射模拟，且尺寸较小、控制装置简单，可应用于靶机上用来模拟各类不同空中目标，提升靶机的功能覆盖。

[1] 丛书全，马金歌.靶机雷达目标特性的计算、测量与模拟[J].无人机.2007(4)：43-44.

CONG Shu-quan，MA Jin-ge.Calculation，Measurement and Simulation of Target Characteristics of Target Radar[J].Unmanned Vehicles,2007(4)：43-44.

[2] 李有才，杨保定，郑春弟.一种RCS值可变的龙伯透镜反射器设计[J].海军大连舰艇学院学报,2010，33(4)：20-23.

LI You-cai，YANG Bao-ding，ZHENG Chun-di.A Design of Luneberg Lens Reflector with Variable RCS Value[J].Journal of Dalian Naval Academy,2010，33(4)：20-23.

[3] 张爱林.雷达无源干扰技术[J].中国科技博览,2016(4)：27-28.

ZHANG Ai-lin.Radar Passive Jamming Technology[J].China Science and Technology Expo,2016(4)：27.

[4] 祝寄徐，裴志斌，屈绍波，等.一种旋转型的角反射器的设计[J].现代电子技术,2013，36(11)：1-4.

ZHU Ji-xu，PEI Zhi-bin，QU Shao-bo，et al.Design of Rotary Angle Corner Reflector[J].Modern Electronics Technique,2013，36(11)：1-4.

[5] 吴春光，何四华，潘玉纯.活动板类角反射器的RCS计算[J].长春理工大学学报,2015，38(3)：116-117.

WU Chun-guang，HE Si-hua，PAN Yu-chun，et al.RCS Computation of the Corner Reflectors with Movable Plates[J].Journal of Changchun University of Science and Technology,2015，38(3)：116-117.

[6] KEE C，WANG C F．Efficient Implementation of High-Frequency SBR-PO Method on GPU[J]．IEEE Antennas and Wireless Propagation Letters，2013，12(2)：941-944．

[7] LI Q，VERNON R J．Theoretical and Experimental Investigation of Gaussian Beam Transmission and Reflection by a Dielectric Slab at 110 GHz[J]．IEEE Transactions on Antennas and Propagation,2006，54(11)：3449-3457．

[8] 金亚秋，刘鹏，叶红霞,等．随机粗糙面与目标复合散射数值模拟理论与方法[M]．北京:科学出版社，2008：56-58.

JIN Ya-qiu，LIU Peng，YE Hong-xia，et al.Theory and Method of Numerical Simulation of Composite Scattering from the Object and Randomly Rough Surface[M].Beijing：Science Press，2008：56-58.

[9] LI Cheng-fan，ZHAO Jun-juan，YIN Jing-yuan．Analysis of RCS Characteristic of Dihedral Corner and Triangular Trihedral Corner Reflectors[C]∥The 5th International Conference on Computer Science & Education．Hefei．August，2010:24-27.

[10] SHAN Xin-jian，YIN Jing-yuan，YU Dan-lin，et al．Analysis of Artificial Corner Reflector’s Radar Cross Section：a Physical Optics Perspective[J]．Arabian Journal of Geosciences，2013，6(8)：2755-2765．

[11] 范学满，胡生亮，贺静波.一种角反射体雷达散射截面积的高频预估算法[J].电波科学学报,2016，31(2)：332-334.

FAN Xue-man，HU Sheng-liang，HE Jing-bo.High Frequency Estimation Algorithm for Scattering Cross - Area of Radar Reflector Radar[J].The Chinese Journal of Radio Science,2016，31(2)：332-334.

[12] 赵俊娟，尹京苑，李成范.基于FEKO平台的人工角反射器RCS模拟[J].微电子学与计算机,2013，30(8)：80-81

ZHAO Jun-juan，YIN Jing-fan,LI Cheng-fan.RCS Simulation of Artificial Angle Reflector Based on FEKO Platform[J].Microelectronics & Computer,2013，30(8)：80-81.

[13] 李亭，韩红斌，刘宇.基于FEKO的雷达目标电磁散射特性研究[J].现代电子技术,2015，38(21)：39-41.

LI Ting，HAN Hong-bin，LIU Yu.Research on FEKO-based Electromagnetic Scattering Characteristics of Radar Target[J].Modern Electronic Technology,2015，38(21)：39-41.

[14] 王明琨，张晨新，张小宽.基于FEKO的典型目标建模与静态RCS数据库建立[J].科技通报,2014，30(11)：190-192.

WANG Ming-kun，ZHANG Chen-xin，ZHANG Xiao-kuan.Typical Target Modeling Based on FEKO and Establishment of Static RCS Database[J].Bulletin of Science and Technology,2014，30(11)：190-192.

[15] 赵雷鸣，李德银，刘昊.基于FEKO软件仿真计算战斗机RCS[J].计算技术与自动化,2010，29(4)：93-96.

ZHAO Lei-ming，LI De-yin，LIU Hao.Simulation of RCS of Battleplan by the Software FEKO[J].Computing Technology and Automation,2010，29(4)：93-96.