基于DS/AHP的贝叶斯网络条件概率值确定方法*
2018-01-02李志强徐廷学顾钧元王瑞奇
李志强,徐廷学,顾钧元,王瑞奇
(海军航空工程学院 兵器科学与技术系,山东 烟台 264001)
0 引言
贝叶斯网络(Bayesian networks,BN)[1-3]在不确定性知识表达与分析中具有独特优势,已广泛应用于工程实践中。BN应用的难点在于模型构建,包括建立拓扑结构和确定模型参数。当前,贝叶斯网络有3种构建方法[4],①利用专家经验知识手动建立BN结构并确定条件概率值(conditional probability table,CPT);②利用数据库学习自动建立BN结构和生成CPT;③两阶段建模,即利用专家经验知识建立BN结构,借助数据库学习生成CPT。大多数BN基于方法3进行构建,然而,利用统计信息进行CPT生成时,在数据训练过程中容易出现NP难题。因此,在大多数情况下,依据模糊函数[5-6]引入专家推断信息确定CPT。杜元伟等在Malcolm Beynon[7]研究工作的基础上对二元状态BN应用DS证据理论/层次分析方法(DS evidence theory/analytic hierarchy process,DS/AHP)确定CPT作了初步研究[8],对于多状态BN结构的CPT确定尚无文献提及。因此,考虑到各个专家在专业技术领域、知识构成、认知程度等方面存在差异的基础上,本文进一步分析专家不确定信息的分析与表达,以确定多状态条件下BN模型的CPT,并应用到工程实践中去。
1 基于DS/AHP方法的知识矩阵构建
1.1 问题描述
在故障树分析法(fault tree analysis,FTA)向贝叶斯网络模型转化过程中,事件之间具有明确的串联、并联、2/3表决等逻辑关系,建立的贝叶斯网络为简单的二元状态或者三元状态,子节点的CPT可以通过串并联逻辑关系确定[9-10]。随着装备朝着大型化、复杂化、精密化等方向发展,二元状态向多状态拓展,因此,对于绝大多数贝叶斯网络而言,节点之间为非确定性逻辑关系。而贝叶斯网络参数学习过程复杂、新型装备数据缺乏,在进行质量状态评估或可靠性分析时,涉及到大量的专业知识、专家经验,从而造成了一定程度上的不确定性[11]。
工程实践中,复杂装备使用面临着复杂多变的工作环境,以至于产生了多种不确定性问题[11-12]:数据缺乏造成的不确定性,不完全知识经验造成的不确定性,不同识别模式造成的不确定性,推理中不同情境假设造成的不确定性,以至于传统的依靠专家经验确定条件概率值的方法受到质疑。传统的条件概率值估计方法假设所有专家都具有按照给定信息需求直接确定CPT的能力,而忽略了各个专家在知识背景、研究领域、认知结构等方面的差异,从而使得个人推断信息存在片面性问题,综合推断结果不具有科学性。在缺乏数据信息的情况下,因为各个专家在研究领域、专业技术、知识背景、逻辑认知等方面存在着不同,提出基于DS证据理论/AHP层次分析法对各个专家的经验信息进行分析与表示、融合多类片面信息降低主观因素引起的认知不确定度,决策判断标准如表1所示。与传统的层次分析法不同,在应用DS/AHP方法对备选方案作出评价时,省去了对每一个方案逐一比较的流程,同时也避免了模型的一致性检验,进而减少了建模的工作量与繁琐的计算过程。此外,各个专家可就明确的备选方案进行指标判断,对于不确定的备选方案可以选择放弃判断。

表1 决策判断标准Table 1 Knowledge scale of decision
1.2 DS证据理论
假设空间Θ表示变量X所有互斥可能值的集合,即Θ是X的一个识别框架[13-14]。假设Θ幂集构成集合2Θ,∀A⊂Θ,如果对于集函数m有2Θ→[0,1],满足:

(1)
则称m是识别框架Θ上的基本信度分配(basic probability assignment,BPA),表示证据对事件A发生与否的支持程度。对于识别框架Θ中的假设A,根据BPA分别求出信任函数和似然函数,构造信任区间[Bel(A),Pl(A)]表示对A的确认程度。对于识别框架Θ上的2个mass函数m1,m2可以根据Dempster规则合成[15-16]:

(2)
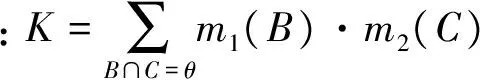
1.3 知识矩阵构建
在对多状态贝叶斯网络进行条件概率赋值时,假设问询了t个技术专家(e1,e2,…,et),从n个维度(c1,c2,…,cn)对条件概率值组合对象x1,x2,…,xp进行了相对于识别框架Θ的重要程度比较,并构建了表2所示的知识矩阵。
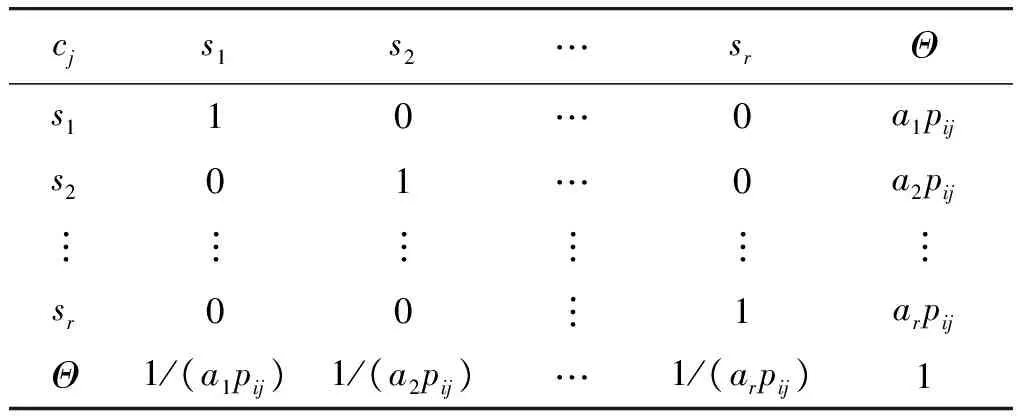
表2 专家ei在属性cj下的知识矩阵Table 2 Knowledge matrix of expert ei according to cj
注:表2中,1表示焦元与本身作出比较;0表示焦元未进行比较;sk表示属性cj下的第k个焦元(k=1,2,…,r.);ak表示sk与识别框架Θ的对比系数;pij表示技术专家ei在属性cj下占有的权重。
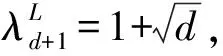

(3)
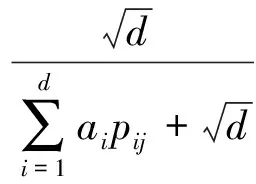
(4)
2 算例分析
以3节点贝叶斯网络为例,如图1所示。贝叶斯网络由3个节点构成,X1,X2为父节点,T为子节点。假设3个节点为4元状态,即状态为s_1,s_2,s_3,s_4,则有如表3所示的条件概率表,子节点T的概率由父节点X1,X2的发生概率确定。

图1 BN节点模型Fig.1 Mode of BN node
现咨询4位技术专家,参照表1确定的决策标准,分别对16个事件建立相对于子节点所处状态偏好程度的知识矩阵。假设各个技术专家权重为0.35,0.30,0.15,0.20。由于篇幅,以节点V1处于状态s_1,节点V2处于状态s_3为例建立判断矩阵,如表4~7所示。
以表5为例,技术专家2能够对子节点T处于状态s_3和s_4作出准确判断。在技术专家2看来,T以几乎相同的概率处于状态s_1和s_2。参照决策判断标准表1,对节点T处于状态{s_1,s_2},s_3和s_4作出相对于辨识框架的可能性进行赋值。
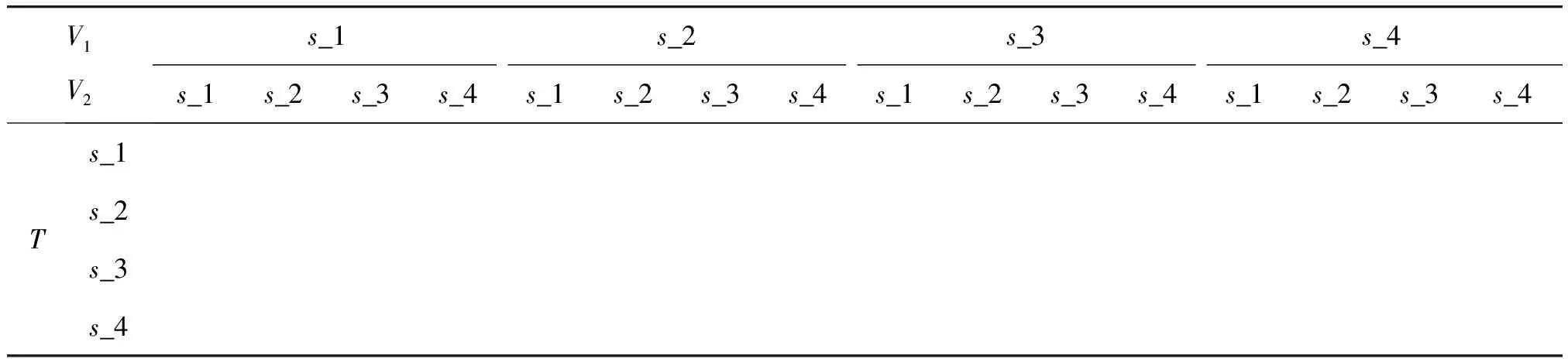
表3 贝叶斯网络CPTTable 3 CPT of BNV1

表4 以专家1偏好建立知识矩阵A1Table 4 Knowledge matrix A1 according to expert 1

表5 以专家2偏好建立知识矩阵A2Table 5 Knowledge matrix A2 according to expert 2

表6 以专家3偏好建立知识矩阵A3Table 6 Knowledge matrix A3 according to expert 3

表7 以专家4偏好建立知识矩阵A4Table 7 Knowledge matrix A4 according to expert 4
根据表4构建知识矩阵A1,求解det(A1-λI1)的最大特征值及对应的特征向量,I1为4×4单位向量。类似地,求解知识矩阵A2,A3,A4,并按照DS证据理论合成原则式(2)对信度函数进行融合,有如表8所示BPA值。
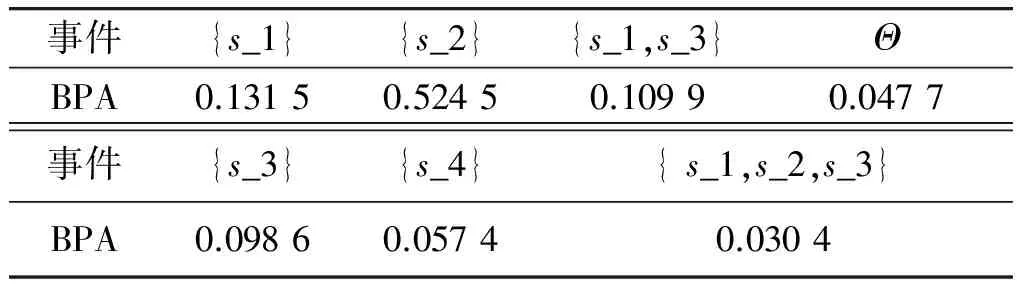
表8 事件BPA值Table 8 BPA of events
从表8可知,节点T状态为s_1的可能性为0.196 6,为s_2的可能性为0.534 6,为s_3的可能性为0.163 7,为s_4的可能性为0.057 4,不确定度为0.047 7。类似的,可以确定其余事件的BPA分配值。
3 不确定性分析
根据知识矩阵特征向量确定的不确定值函数式(4)描出矩阵A1,A2,A3和A4的不确定值曲线,由专家权重值确定不同专家经验知识下的不确定值,如图2所示。
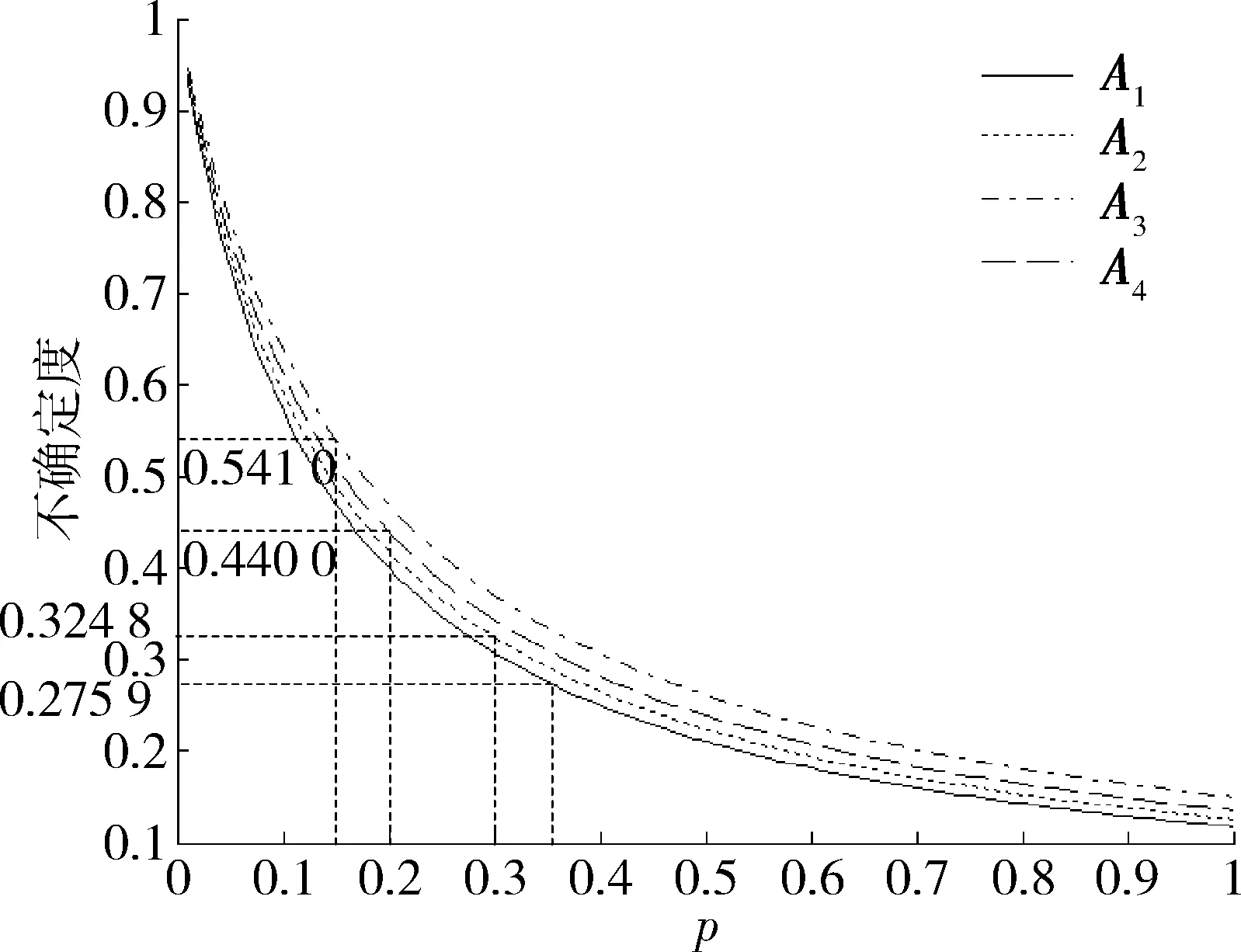
图2 知识矩阵不确定度Fig.2 Uncertainty of knowledge matrix
从图2中可以看出,在同一个知识矩阵中,专家的权威越大,不确定值就越低;同一个专家建立的知识矩阵越详细,不确定值就越低。尽管个别知识矩阵不确定值比较高,但在融合多位专家信息之后,不确定度将呈指数降低,以第2部分的融合结果为例,不确定值为0.047 7。
3.1 最大不确定度
在极端情况下,当p=0时(为不加区分,在此后的讨论中以p代替pij),知识矩阵的不确定度最大,表示依靠专家经验知识无法识别出优选方案,不确定度为1,即m(Θ)=1。
3.2 最小不确定度
在确定专家权重p值的情况下,建立的知识矩阵大小与不确定度有关,当知识矩阵为满矩阵时,不确定度最低,当知识矩阵不为满秩时,不确定度随着秩的降低逐渐增加。
(1) 备选方案数大于或等于判断标准等级
当备选方案数大于或者等于判断标准等级时,假设专家只能区分备选方案的r组。定义s1,s2,…,sr为各方案组,将最大的判断标准等级(r+1)分配给s1,从大到小将规模值逐个分配给s2,s3,…,sr。此时,经验知识的最大值(即最小的不确定度)在知识矩阵中表示为
.
(5)
根据知识矩阵(5)可以确定备选方案si(i=1,2,…,r)相对识别框架Θ的基本概率分配函数,定义m5为(5)的BPA,则知识矩阵的不确定度函数表示为

(6)
以r=5为例,a1=6p,a2=5p,…,a5=2p,则BPA函数表达式为
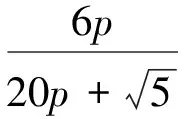


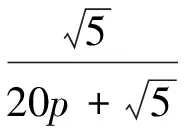
根据BPA函数拟出相应曲线,如图3所示,可知,当r=5时,知识矩阵的最小不确定度为0.100 6。
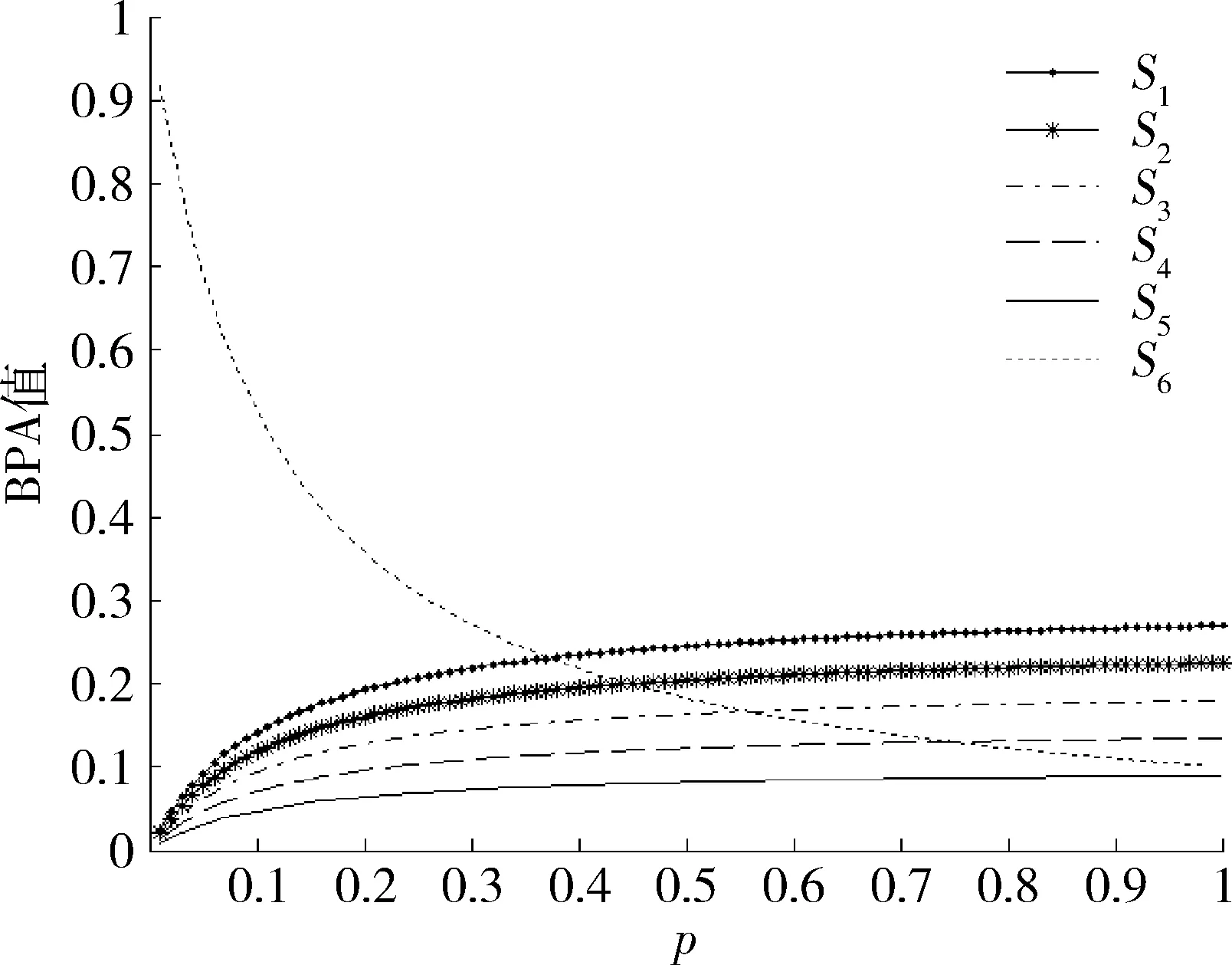
图3 d≥r时的知识矩阵BPA曲线Fig.3 BPA curves of knowledge matrix when d≥r
(2) 备选方案数小于判断标准等级
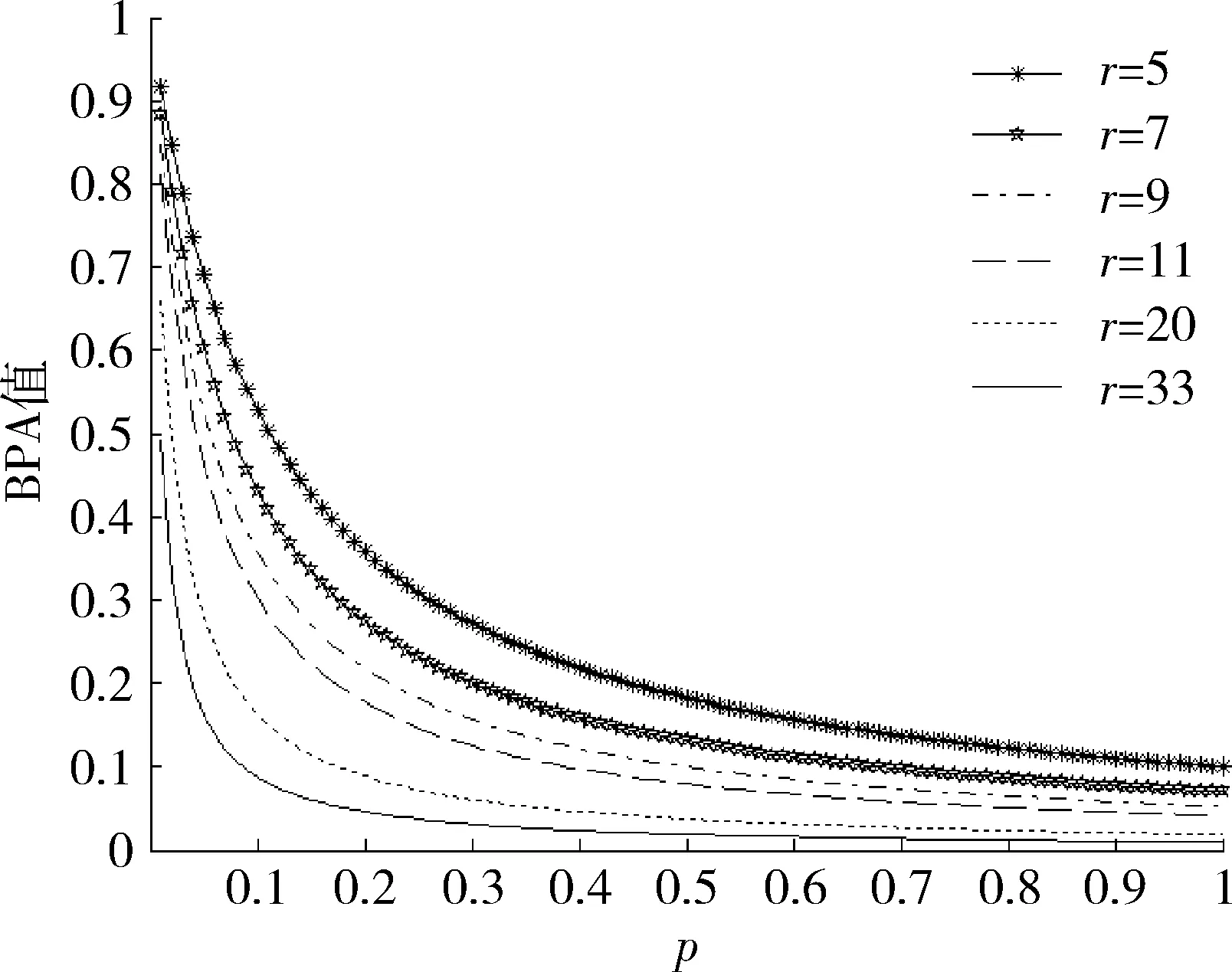
现讨论备选方案d小于判断标准等级r的情况(d (7) 定义m6为与知识矩阵(7)对应的BPA,则不确定度表示为 (8) 以r=5,d=2为例,知识矩阵各BPA为 根据BPA函数拟出相应曲线,如图4所示,可知,知识矩阵的最小不确定度为0.113 9。对比m6与m2,m3可以看出,不同的专家对于同一个方案组有不同的看法,给出不同的具体指标值,这也正好反映了不同专家在知识背景、认知程度等方面的差异,造成了不同程度的不确定度。 图4 d (3) 不同判断标准等级下的不确定度 从式(6)可以看出,判断标准等级划分越详细,不确定度越低,如图5所示。当r=9时,不确定度降低到0.052 6,而当r=33时,不确定度为0.009 6,即降低到不足1%,然而,等级划分与人的主观判断能力有关。以层次分析法为例,根据评判标准,当r=9时,普通人可以进行两两比较,当判断等级更多时,就容易产生不易区分的模糊区域。因此,r=33或者更大时,判断标准更难划分,也无法判断。由于DS证据理论具有融合不确定信息,降低专家经验知识不确定度的优势,也就没有必要将判断标准划分得非常细。此外,贝叶斯网络多状态划分等级一般不超过5,表1建立的判断标准满足应用需求。 图5 不同r值下的不确定度Fig.5 Uncertainty of knowledge matrix under different r 针对多状态贝叶斯网络条件概率值难以确定的问题,本文在现有研究的基础上,提出了基于DS证据理论/层次分析法的建模方法,借助专家经验构建知识矩阵,经求解特征值、特征向量,确定了各个状态的基本概率分配值,为多状态复杂系统可靠性建模与分析提供了新的方法与思路。该方法使得复杂系统多状态可靠性建模与分析从确定的逻辑结构关系向非确定的逻辑结构关系过渡,拓展了可靠性分析的研究领域。同时,DS证据理论/层次分析法克服了传统层次分析法进行两两比较和一致性检验的繁琐过程,从而可以对确定与不确定信息进行选择性表达,有效地降低了模型的不确定度,大大提高了模型的科学性与可信性。 [1] ALYSON G W,APARNA V H.Bayesian Networks for Multilevel System Reliability[J].Reliability Engineering and System Safety,2007(92):1413-1420. [2] PIERO B,LUCA P,LUSINE M,et al.Comparing the Treatment of Uncertainty in Bayesian Networks and Fuzzy Expert Systems Used for a Human Reliability Analysis Application[J].Reliability Engineering and System Safety,2015(138):176-193. [3] 王波,吴华丽,王灿林.基于贝叶斯网络的复杂装备D-S诊断[J].计算机仿真,2009,26(4):34-37. WANG Bo,WU Hua-li,WANG Can-lin.D-S Diagnosis Based on Bayes Network[J].Computer Simulation,2009,26(4):34-37. [4] ANDRÉs R M,SERAFn M.An Interactive Approach for Bayesian Network Learning Using Domain/Expert Knowledge[J].International Journal of Approximate Reasoning,2013(54):1168-1181. [5] 顾潮琪,张才坤,周德云,等.基于直觉模糊贝叶斯网络多态系统可靠性分析[J].西北工业大学学报,2014,32(5):744-748. GU Chao-qi,ZHANG Cai-kun,ZHOU De-yun,et al.Reliability Analysis of Multi-State Systems Based on Intuitionistic Fuzzy Bayesian Networks[J].Journal of Northwestern Polytechnical University,2014,32(5):744-748. [6] 陈东宁,姚成玉.基于模糊贝叶斯网络的多态系统可靠性分析及在液压系统中的应用[J].机械工程学报,2012,48(16):175-183. CHEN Dong-ning,YAO Cheng-yu.Reliability Analysis of Multi-State System Based on Fuzzy Bayesian Networks and Application in Hydraulic System[J].Journal of Mechanical Engineering,2012,48(16):175-183. [7] MALCOLM B.DS/AHP Method:A Mathematical Analysis,Including an Understanding of Uncertainty[J].European Journal of Operational Research,2002(140):148-164. [8] 杜元伟,石方园,杨娜.基于证据理论/层次分析法的贝叶斯网络建模方法[J].计算机应用,2015,35(1):140-146. DU Yuan-wei,SHI Fang-yuan,YANG Na.Construction Method for Bayesian Network Based on Dempster-Shafer/Analytic Hierarchy Process[J].Journal of Computer Application,2015,35(1):140-146. [9] HELGE L,LUIGI P.Bayesian Networks in Reliability[J].Reliability Engineering and System Safety,2007(92):92-108. [10] 尹晓伟,钱文学,谢里阳.基于贝叶斯网络的多状态系统可靠性建模与评估[J].机械工程学报,2009,45(2):206-212. YIN Xiao-wei,QIAN Wen-xue,XIE Li-yang.Multi-State System Reliability Modeling and Assessment Based on Bayesian Network[J].Journal of Mechanical Engineering,2009,45(2):206-212. [11] 孟欣佳,敬石开,刘继红,等.多源不确定性下基于证据理论的可靠性分析方法[J].计算机集成制造系统,2015,31(3):648-655. MENG Xin-jia,JING Shi-kai,LIU Ji-hong,et al.Relaibility Analysis Method Based on Evidence Theory Under Multi-Source Uncertainty[J].Computer Integrated Manufacturing Systems,2015,31(3):648-655. [12] 彭文胜,张建国,王丕东,等.混合不确定信息航天机构可靠性综合分析方法[J].宇航学报,2015,36(5):596-604. PENG Wen-sheng,ZHANG Jian-guo,WANG Pi-dong,et al.Comprehensive Reliability Analysis of the Aerospace Mechanism with Hybrid Uncertainty Information[J].Journal of Astronautics,2015,36(5):596-604. [13] 余思奇,景博,黄以锋.基于D-S证据理论的测试性综合评估方法[J].计算机应用研究,2014,31(7):2071-2073. YU Si-qi,JING Bo,HUANG Yi-feng.Comprehensive Testability Evaluation Method Based on D-S Evidence Theory[J].Application Research of Computers,2014,31(7):2071-2073. [14] 关欣,孙贵东,郭强,等.基于区间数和证据理论的雷达辐射源参数识别[J].系统工程与电子技术,2014,36(7):1269-1274. GUAN Xin,SUN Gui-dong,GUO Qiang,et al.Radar Emitter Parameter Recognition Based on Interval Number and Evidence Theory[J].Systems Engineering and Electronics,2014,36(7):1269-1274. [15] 丛林虎,徐廷学,卜祝涛,等.基于故障数据的导弹突发故障预测方法[J].战术导弹技术,2014(2):43-47. CONG Lin-hu,XU Ting-xue,PU Zhu-tao,et al.Missile Sudden Fault Prediction Based on Fault Data[J].Tactical Missile Technology,2014(2):43-47. [16] 王杨,刘以安,张强.改进的D-S证据理论在战场目标识别中的应用[J].弹箭与制导学报,2015,35(2):156-158. WANG Yang,LIU Yi-an,ZHANG Qiang.Application of Target Identification in Battlefield Based on Improved D-S Evidence Theory[J].Journal of Projectiles,Rockets,Missiles and Guidance,2015,35(2):156-158.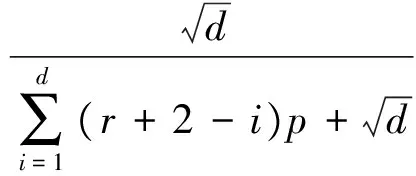
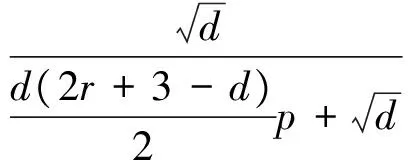
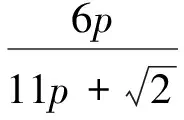
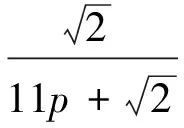

4 结束语
