反导案例匹配中的距离度量算子*
2018-01-02田振浩邢清华李龙跃
田振浩,邢清华,李龙跃
(空军工程大学 防空反导学院,陕西 西安 710051)
0 引言
弹道导弹具有高空、高速和不易被发现的特性,且反导作战是体系化作战,装备之间协同复杂,需要同时处理的信息量大,因此需要提高反导作战指挥决策的智能化和自动化水平,确保决策的时效性和准确性[1-4]。案例推理是人工智能领域一个较新的基于知识的问题求解和学习方法,通过重用以往解决相似问题的方法来解决现有问题[5-7]。将案例推理运用到反导作战中,通过重用以往相似案例,预先制定作战方案,可以提高反导作战指挥决策的效率[8-9]。
案例相似度是确定以往案例是否可以借鉴到现有案例的标准。常用的相似度量方法有基于距离的方法、基于余弦的方法、基于语义网[10-11]的方法等,其中,基于距离的方法是最常用的,主要包括数值间的距离度量和区间数间的距离度量[12-15]。反导案例属性种类众多,方法各异,文献[12]中有相关介绍,本文主要研究适用于反导作战的数值距离度量方法。针对案例相似度量中要求对较相似案例有更高的区分度的问题,本文提出一种新的距离度量算子,经数学公式推导,证明了该算子的有效性,通过绘制几种距离算子的变化曲线及实验分析,证明了本文所提算子比现有的距离度量算子有较高的灵敏度。
1 数值距离度量函数
距离指2个个体之间的空间相隔长度,也可以称为2个个体之间的差距,距离越大说明个体间的差异越大。在案例推理中,距离度量被用于案例的相似性度量中,通过寻找距离最小的个案例,找出相似案例。
假设,有n个数值的向量X和向量Y,其中X=(x1,x2,…,xn),Y=(y1,y2,…,yn),由于进行数据分析时,常常需要对所有数据进行归一化处理,因此,在这里规定xi,yi∈[0,1](i∈[1,n])。定义X和Y之间的距离为d(X,Y),且d(X,Y)应满足以下3条性质:
(1) 有界性:0≤d(X,Y)≤1;
(2) 自反性:d(X,Y)=0,当且仅当xi=yi,i=1,2,…,n;
(3) 交换性:d(X,Y)=d(Y,X)。
最常用的距离度量函数[12]是欧式距离(Euclidean distance):
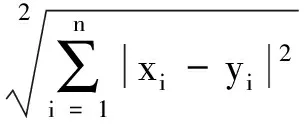
(1)
欧式距离描述的是2点之间的几何直线距离,此外还有曼哈顿距离(Manhattan distance):
(2)
切比雪夫距离(Chebyshev distance):
(3)
类似于式(1)~(3)中xi-yi称为距离度量算子,用于计算2个数值之间距离,xi-yi是直接距离算子。对于2个给定的数值x和y,常用的距离度量算子有直接距离算子(straight distance):
dstr(x,y)=x-y.
(4)
卡方距离算子(Chi-square distance):

(5)
海明距离算子(Hamming distance):
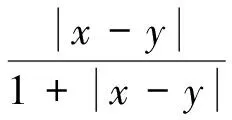
(6)
距离度量算子可以看做是对一维数值向量的距离度量方法,因此也需要满足上述的3条性质。将卡方距离算子和海明距离算子带入欧式距离度量函数中,可以得到改进的欧式距离度量函数:
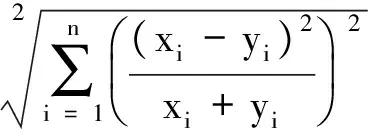
(7)

(8)
2 新的距离度量算子
在案例检索中相似度算法分辨率越高,可以过滤掉的不相似案例越多。本文在不考虑主观因素的基础上,提出一种能客观的提高分辨率的距离度量算子为

(9)
将该算子带入欧式距离中,得到改进的欧式距离:

(10)
2.1 合理性分析
通过判断式(9)是否满足距离度量的3条性质,分析其合理性。
易知,当x=y=0时,dnew(x,y)=0不存在,所以增加算子的适用条件x,y不同时为0,并且规定,当x=y=0时,dnew(x,y)=0。修正后的算子可写为
(11)
运用数学知识分析式(11)是否满足3条性质。
(1) 有界性:0≤dnew(x,y)≤1。
证明:
1) 当x=y=0时
dnew(x,y)=0;
2) 当x=y≠0时
;
3) 当x≠y时

所以dnew(x,y)≥0。

综上所述,0≤dnew(x,y)≤1。
(2) 自反性:dnew(x,y)=0,当且仅当x=y。
证明:
必要性:见有界性的证明。
充分性:采用反证法证明。
假设存在x≠y,使得dnew(x,y)=0。


2) 当x=y=0时,dnew(x,y)=0,与假设矛盾,因此假设不成立,即不存在x≠y,使得
dnew(x,y)=0。
综上所述,当且仅当x=y时,dnew(x,y)=0。
(3) 交换性:dnew(x,y)=dnew(y,x)。
证明:
当x=y=0时,
dnew(x,y)=dnew(y,x)=0;
当x=y≠0时,
dnew(x,y)=dnew(y,x)=00+=0;
当x>y时,

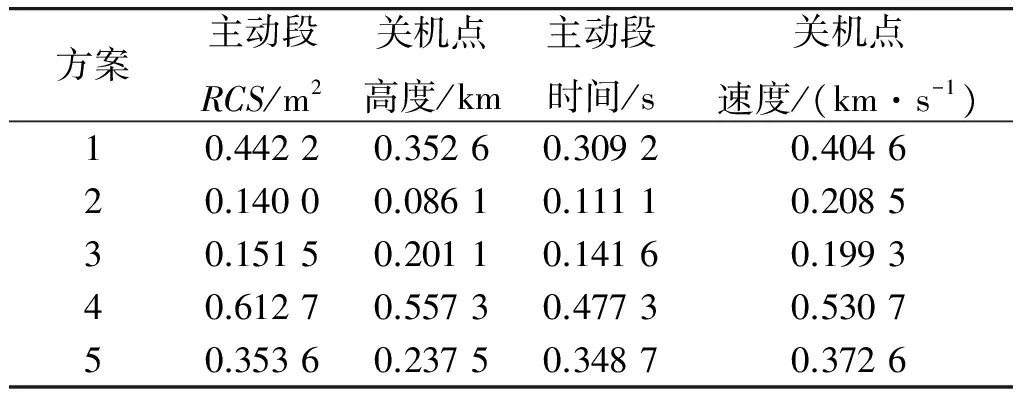
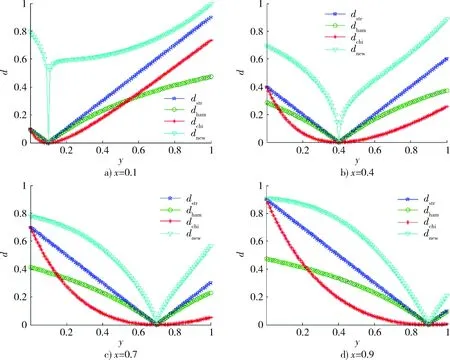
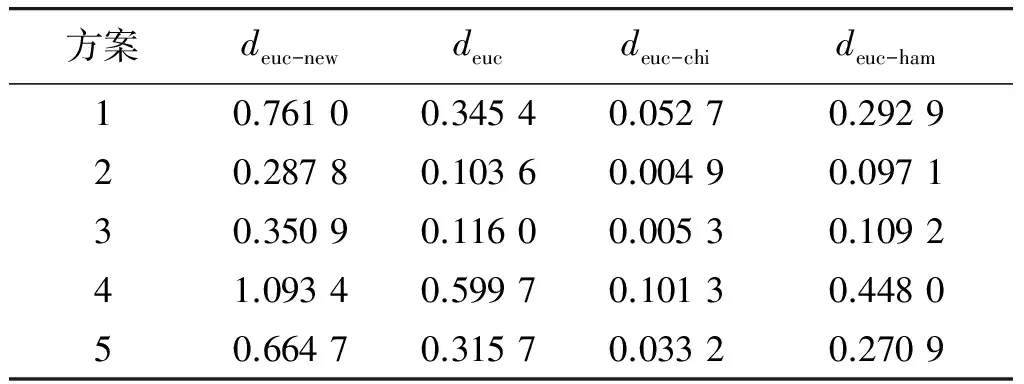
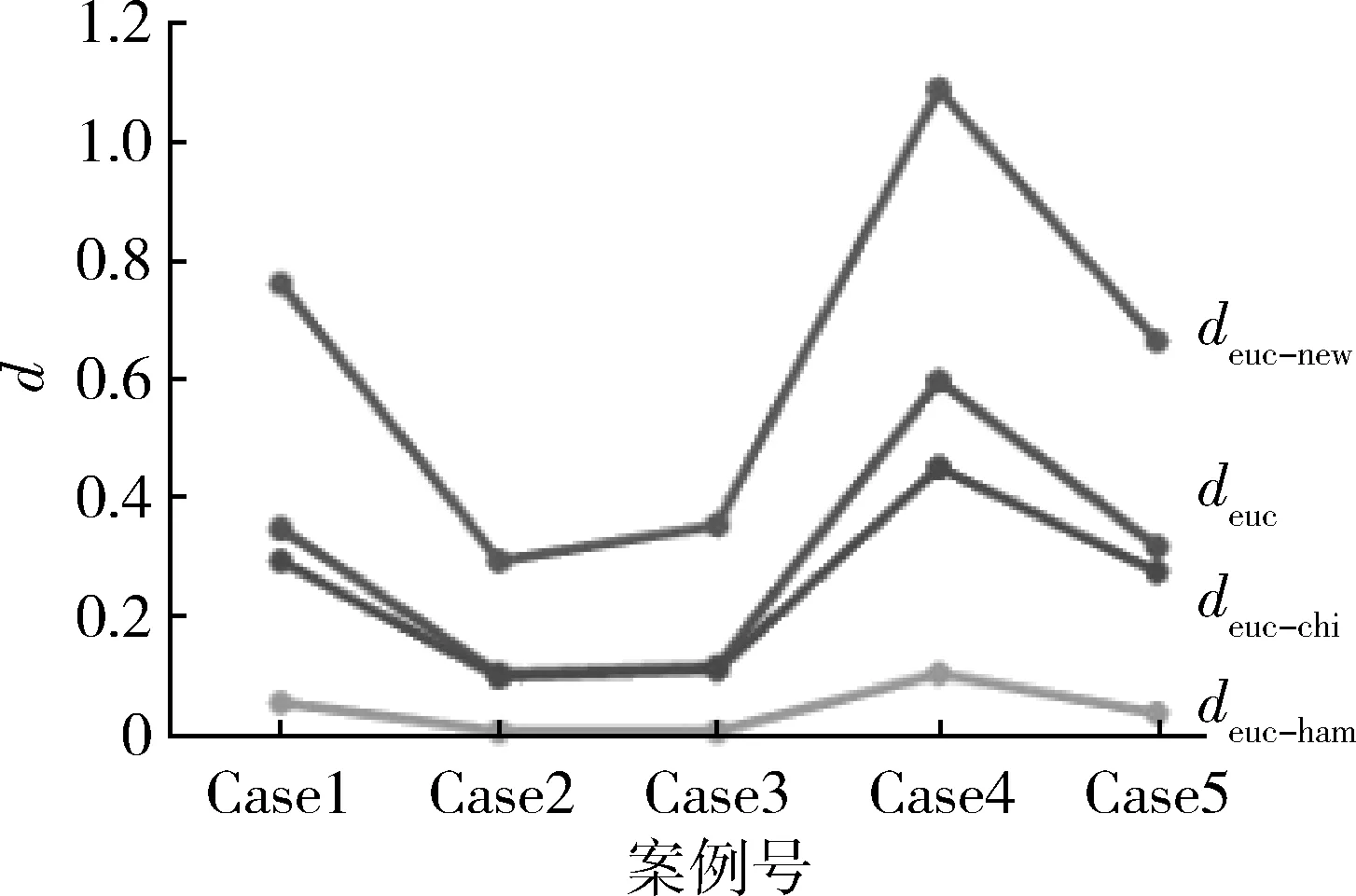
当x 综上所述dnew(x,y)=dnew(y,x)。 数值距离度量算子灵敏度是指随着2个数值间差距的增大,所计算出的距离增加程度。增加单位差距内,距离增加程度越大,表明此处灵敏度越高。绘制式(9)中dnew随x,y变化的三维曲面图,如图1所示。 图1 dnew三维曲面图Fig.1 3D surface of dnew 从图1可以看出: (1) 纵轴坐标dnew范围在[0,1]之间,验证了性质(1)。 (3) 曲面关于平面x=y对称,即dnew(x,y)=dnew(y,x),验证了性质(3)。 (4) 距离平面x=y越远,dnew值越大,且曲面坡度由陡变缓,表明式(9)在x=y附近灵敏度高,远离x=y灵敏度逐渐降低。 在案例推理中,为了找出与新案例相似的案例,常常需要计算已有案例与新案例之间属性的相似度,这里假设x为新案例属性,y为已有案例属性,分别设定x=0.1,x=0.4,x=0.7,x=0.9,绘制式(4)~(11)中dstr,dchi,dham,dnew随y的变化曲线,如图2所示。 从图2可以看出:4条曲线在y=x处均与y轴相交,即d=0,表明4个公式均可以找出最相似的案例来;由式(11)绘制的曲线明显在其他3条曲线上方,且在点y=x附近,曲线斜率最大(图2a)中由式(11)绘制的曲线在y=x附近看似有突变,是因为曲线绘制时参考点选取较少,且曲线斜率大,实际上曲线是连续变化的)表明式(11)对于2个相差很小的数值有较高的分辨率,对于较相似案例有很好的区分能力。 在反导作战中,将以往来袭目标信息或已知型号弹道导弹信息存储到数据库中,通过实际作战中预警卫星等传感器探测的目标信息与数据库中信息的对比,可以找出相似的或同一型号弹道导弹,以获得目标的其他信息,为拦截提供保障。本文假设一组弹道导弹数据,如表1所示。用来检验式(11)所提的距离度量算子。 利用式(12)对上述数据进行归一化处理 (12) 采用式(11)计算5个案例与新案例各属性间的距离dnew,计算结果见表2。 表1 实验数据Table 1 Experimental data 表2 5个案例与新案例各属性间的dnewTable 2 dnew between newcase and five cases 分析表2中数据,最小值0.086 1,是Case2与Newcase关机点高度值(96,93)之间的距离;数据分布在0.086 1~0.612 7之间,跨度比较大,分布比较散,表明本文所提算子可以提高数据间距离的分辨率。 图2 4距离度量算子在x为定值时随y的变化曲线Fig.2 Curves of four distance metric operators 采用式(10) 计算5个案例改进后的欧式距离,得到: deuc-new(Case1,Newcase)=0.761 0, deuc-new(Case2,Newcase)=0.287 8, deuc-new(Case3,Newcase)=0.350 9, deuc-new(Case4,Newcase)=1.093 4, deuc-new(Case5,Newcase)=0.664 7. 比较计算结果,0.287 8<0.350 9<0.664 7<0.761 0<1.093 4。得到与New最相近的案例是Case2. 分别采用式(1),(7),(8)计算同样的数据,并与式(10)的结果进行比较。 各距离度量方法结果比较如表3所示,用Excel绘制表3中数据的折线图如图3所示。 表3 各距离度量方法结果比较Table 3 Results of four distance measurement methods 图3 各距离度量方法结果比较Fig.3 Results of four distance measurement methods 根据图3及表3中数据,4个式子都可以找到最相近的案例Case2,即4种方法计算的结果没有明显差别,表明式(10)是可行的;且deuc-new曲线波动幅度比其他3条大,计算结果间的差距也比其他3条大,表明式(10)能提高数据间的分辨率。 现有的相似性度量方法对于较相似案例的区分度不高,用于在反导作战中,将无法更精确的筛选出满足相似度阈值的相似案例。本文提出了一种新的距离度量算子,用于计算数值属性间的距离,经分析验证,该算子满足距离度量的3条性质,且对于差别较小的数比其他算子有更好的区分能力。将该算子用于欧氏距离中,用改进后的欧式距离求弹道导弹案例间的总体距离,验证了本文所提算子的有效性。本文所提的方法用于大量案例的相似性度量中,更容易筛选掉大量不是很相似的案例,效果也更加明显。 [1] JONATHAN P N,ROBERT E B,CHAD M S.Implementation of an Accelerated Assessment Process for the Terminal High Altitude Area Defense System:Initial Operational Test and Evaluation Supporting a Production Decision[J].ITEA Journal of Test and Evaluation,2012,33(2):135-144. [2] DHAIFALLA K Al-Mutairi,Asok K Nanda,Richard M Soland.Monotonicity and Comparability in Ballistic Missile Defense Systems[J].Journal of Statistical Planning and Inference,2011(141):2191-2200. [3] 李龙跃,刘付显,赵麟锋,等.攻防对抗中指数射击策略最优性分析[J].兵工学报,2015,36(5):2206-2211. LI Long-yue,LIU Fu-xian,ZHAO Lin-feng,et al.Optimality Analysis of Index Policy for Offense-Defense Shooting Process[J].Acta Aarmaenarll,2015,36(5):2206-2211. [4] 李龙跃,刘付显,赵麟锋.对多波次目标直接分配到弹的反导火力规划方法[J].系统工程与电子技术,2014,36(11):2206-2212. LI Long-yue,LIU Fu-xian,ZHAO Lin-feng.Direct Interceptor Allocation Method in Antimissile Firepower Planning for Multiple Ware Targets[J].Systems Engineering and Electronics,2014,36(11):2206-2212. [5] SENE A,KAMSU-FOGUEM B,RUMEAU P.Telemedicine Framework Using Case-Based Reasoning with Evidences[J].Computer Methods and Programs in Biomedicine,2015,121(1):21-35. [6] ROLDAN REYES E,NEGNY S,CORTES ROBLES G,et al.Improvement of Online Adaptation Knowledge Acquisition and Reuse in Case-Based Reasoning:Application to Process Engineering Design[J].Engineering Applications of Artificial Intelligence,2015,41(1):1-16. [7] Aman Tyagi,Preetvanti Singh.ACS:Asthma Care Services with the Help of Case Base Reasoning Technique[J].Procedia Computer Science,2015,48(1):561-567. [8] 范海雄,刘付显,邹志刚.反导作战预案形式化建模研究[J].现代防御技术,2013,41(1):1-8. FAN Hai-xiong,LIU Fu-xian,ZOU Zhi-gang.Antimissile Preparative Solution Formal Modeling Method[J].Modern Defence Technology,2013,41(1):1-8. [9] 范海雄,刘付显,夏璐.融合可修性度量和双线学习的反导预案修正[J].现代防御技术,2013,41(4):54-60. FAN Hai-xiong,LIU Fu-xian,XIA Lu.Antimissile Preparation Case Revise Based on Revise Measurement and Double Learning[J].Modern Defence Technology,2013,41(4):54-60. [10] Montserrat Batet,David Sánchez,Aida Valls,et al.Semantic Similarity Estimation from Multiple Ontologies[J].Applied Intelligence,2013,38(1):29-44. [11] Steffen Staab.Ontologies and Similarity[J].Lecture Notes in Computer Science,2011(1):11-16. [12] 田振浩,邢清华,李龙跃.基于混合相似度的反导作战案例检索方法[J].装甲兵工程学院学报,2016,30(6):55-59. TIAN Zhen-hao,XING Qing-hua,LI Long-yue.Case Retrieval Method of Antimissile Operation Based on Hybrid Similarity[J].Journal of Academy of Armored Force Engineering,2016,30(6):55-59. [13] Ontanon Santiago,Plaza Enric.Similarity Measures over Refinement Graphs[J].Mach Learn,2012,87(1):57-92. [14] Stefanescu Dan,Banjade Rajendra,Rus Vasile.A Sentence Similarity Method Based on Chunking and Information Contentn[J].Lecture Notes in Computer Science,2014(1):442-453. [15] Batet Montserrat,Sánchez David,Valls Aida,et al.Semantic Similarity Estimation from Multiple Ontologies[J].Applied Intelligence,2013,38(1):29-44.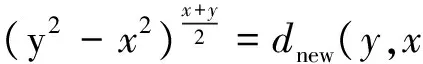
2.2 灵敏度分析
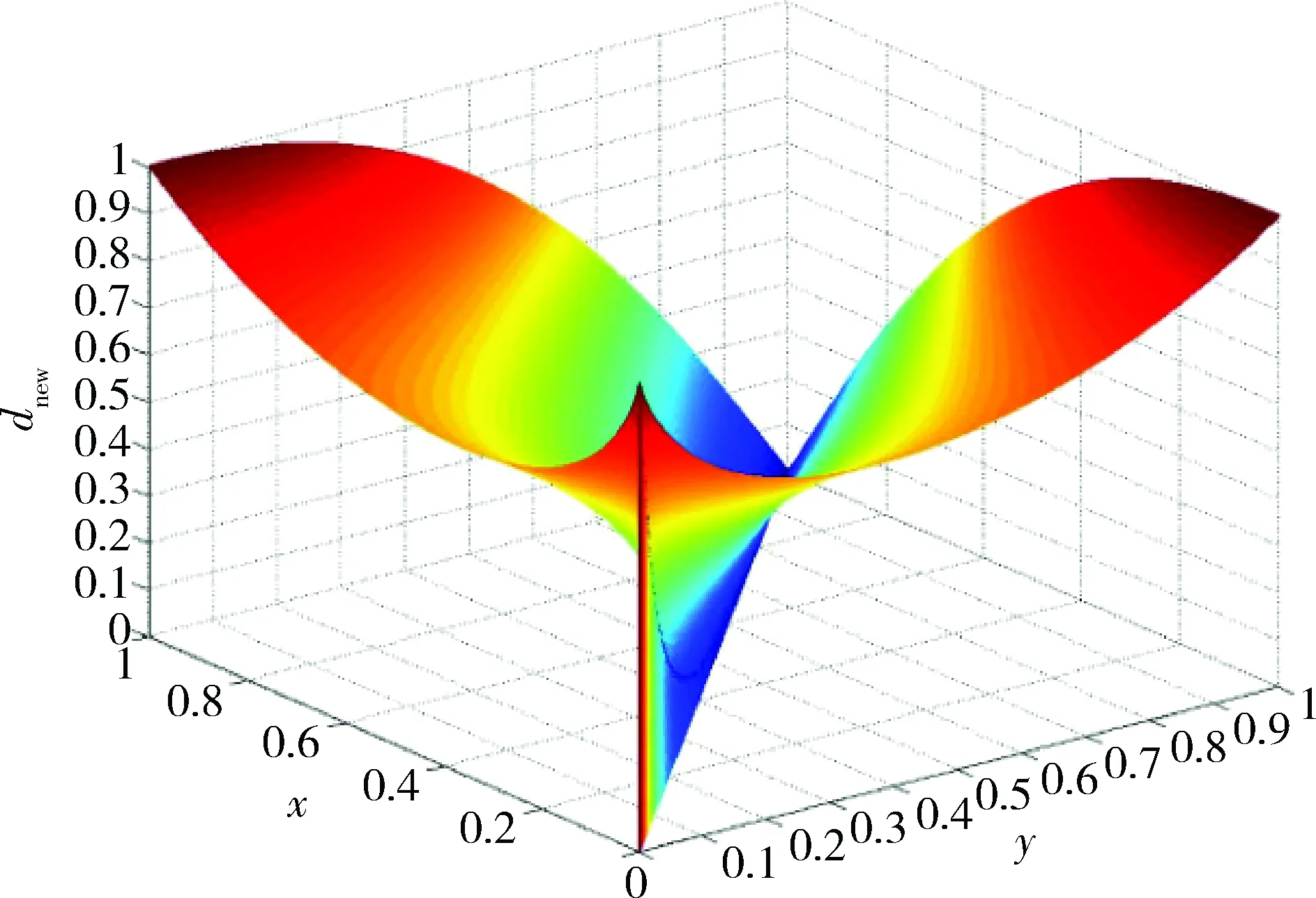

3 方法有效性验证
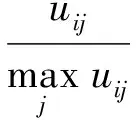
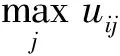

4 结束语
