模糊聚类的多雷达航迹关联算法*

张良，陶海军，杨钒，王惊晓

(陆军军官学院a.军用光电工程教研室;b.研究生管理大队;c.高等教育研究室，安徽 合肥 230051)

0 引言

随着科技高速发展，现代作战越来越依赖高精度的雷达系统进行有效的对敌军目标进行定位，这就要求在战争中需要依靠多雷达对设定目标进行全方位、全天时以及全天候的定位探测，多雷达系统分布独立定位设定目标，这就需要设置多个传感器对目标航迹进行测量，对被测目标航迹进行关联及融合处理，得到设定目标航迹的状态估计，形成系统航迹[1]。

雷达系统对目标进行精确定位的前提是对目标的航迹进行精确估计，多雷达系统的各个传感器将各自测量信号发送到其自带跟踪器形成局部航迹周期性的送往融合中心进行航迹融合，形成系统航迹，因此，对于此多传感器系统测量的航迹关联是影响雷达系统数据融合精度的较为重要的因素[2]。

目前对于航迹关联较为常用的方法主要为：人工智能算法以及灰色理论等。人工智能算法的计算速度较快，但是需要大量的精确数据作为其关联基础，并且对参数实测数据精度要求较高[3]。而灰色关联理论对于参数实测数据质量要求较低，但是其算法本身只能是对目标航迹的局部进行最优化处理[4]。

目前已经报道文献中，主要是基于模糊理论[5-6]以及统计理论[7-8]对目标航迹进行关联处理的。传统的统计理论并不能实现对设定目标进行精确的航迹测量，如果测量信号中有大量的噪音存在，导致其不能很好的对目标航迹信息进行关联融合。

综上所述的各类航迹融合的问题，本文基于模糊理论对多目标模糊航迹进行关联运算，对多传感器测量到的多个航迹进行模糊化聚类统计，当目标众多导致采集的数据量较大时，采用分步法对航迹信息进行模糊聚类处理，实现对多目标航迹信息数据的精确关联融合。

1 分布的基于模糊聚类的多雷达航迹关联算法

1.1 算法描述

(1) 设X=(X1，X2,…,Xn)′与Y=(Y1，Y2,….Yn)′为传感器1和2的一组量测数据(列向量),模糊聚类的损失函数为[9]

(1)

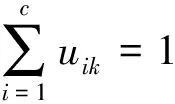
马氏距离为

d=ΔTG-1Δ,

(2)

式中:Δ=X-Y。

雷达采集数据聚类算法中心为

∀i,

(3)

采集样本的权值xk与各采集数据的聚类中心vi的隶属度方程为

∀i，k.

(4)

本文在对多雷达系统采集的数据进行航迹聚类关联时，应先给出数据聚类关联中心点的初始值V(0)，通过迭代算法求得U(k)，V(k+1)，k=1，如果

(5)

ε为迭代收敛的判断精度要求，并ε>0。

G=E[ΔΔT]=PX+PY-PXY-PYX，PX和PY分别是X和Y的协方差矩阵，PXY是X和Y的互协方差矩阵，PYX是Y和X的互协方差矩阵，有

PX=E{[X-E(X)][X-E(X)]T},

(6)

PY=E{[Y-E(Y)][Y-E(Y)]T},

(7)

PXY=E{[X-E(X)][Y-E(Y)]T},

(8)

PYX=E{[Y-E(Y)][X-E(X)]T}.

(9)

如果这2组量测数据是互相独立的，那么PXY和PYX都是0矩阵，相应的算法是加权统计距离检验法；如果这2组量测数据不是独立的，PXY和PYX不一定是0矩阵，相应的算法是修正的加权统计距离检验法。

(2)X和Y是否代表同一个目标的检验[10]

H0：d<χ2，X和Y是同一目标;

H1：d>χ2，X和Y不是同一目标。

在H0的假设条件下，统计距离d满足自由度为状态向量维数的χ2分布，即

(10)

式中:τ(n)为伽马(Gamma)分布。满足τ(n)=(n-1)!。

图1 自由度为2的χ2分布Fig.1 χ2 distribution degree of freedom of 2

1.2 算法步骤

算法步骤如下[11-12]：

(1) 计算真实量测和预测值的距离

).

(11)

(2) 计算马氏距离

(12)

(3) 对马氏距离进行变换，这里采用变换形式如下：

y=e-x,

(13)

式中:x为马氏距离;y为变换后的结果。

这里也可以考虑其他变换形式。

(4) 归一化

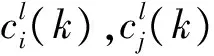
(14)

(15)

(16)

(17)

得到的li(k)是k时刻最终的点迹选取个数。

(6) 计算li(k)个关联概率，对这li(k)个关联概率进行归一化处理。

2 算法仿真[14-15]

假设跟踪门内有3个量测，X(k)=(S(k)，ST(k))T表示水平位置和水平速度构成的向量，初始值取(0, 5)T。Z(k)=S(k)表示水平位置，初始值取0。其他量取为T=1，F=(1,T；0, 1)，G=(T·T/2，T)T，H=(1, 0),PD=1，PG=0.9，λ=0.5，γ=0.5，η=0.9。状态噪声为0均值、方差0.5的高斯白噪声；量测噪声为0均值、方差分别为0.5,1,3(对应3个点迹)的高斯白噪声。仿真结果如图2所示。

仿真结果：该算法通过阈值的选取，在保证计算精度的前提下，解决了传统滤波跟踪算法中计算量太大的问题，节省了计算时间，可以满足实时性的要求。从图2中可以看到，与量测值比较，利用该算法获得的估计值更加接近实际数值。

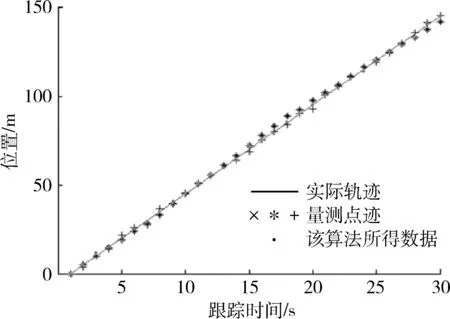
图2 新的点迹选取方法仿真Fig.2 Simulation of new flight choosing method

为验证本文给出的关联算法和航迹管理表的可行性，考虑一个比较复杂的情形：①航迹距离较近的目标；②机动目标航迹；③交叉飞行目标航迹。观测过程中有新的目标出现以及某些目标的终止。具体仿真情景如下：10个匀速直线飞行的目标，其运动速度为560 m/s，其航迹编号分别是从上到下为1～10。航迹编号1～5是航迹距离较近的目标，其间距均为560 m。6～8是机动目标航迹的目标，8～10为交叉飞行目标航迹，相邻直线间的夹角是6°。假定在1～10 s雷达仅能检测到航迹编号为4,5和9,10 4个目标的量测，从11～47 s所有目标的量测都可检测到。从48～60 s，只能量测到航迹号从3～8的目标。雷达的距离量测误差在x,y2个方向上都是60 m。

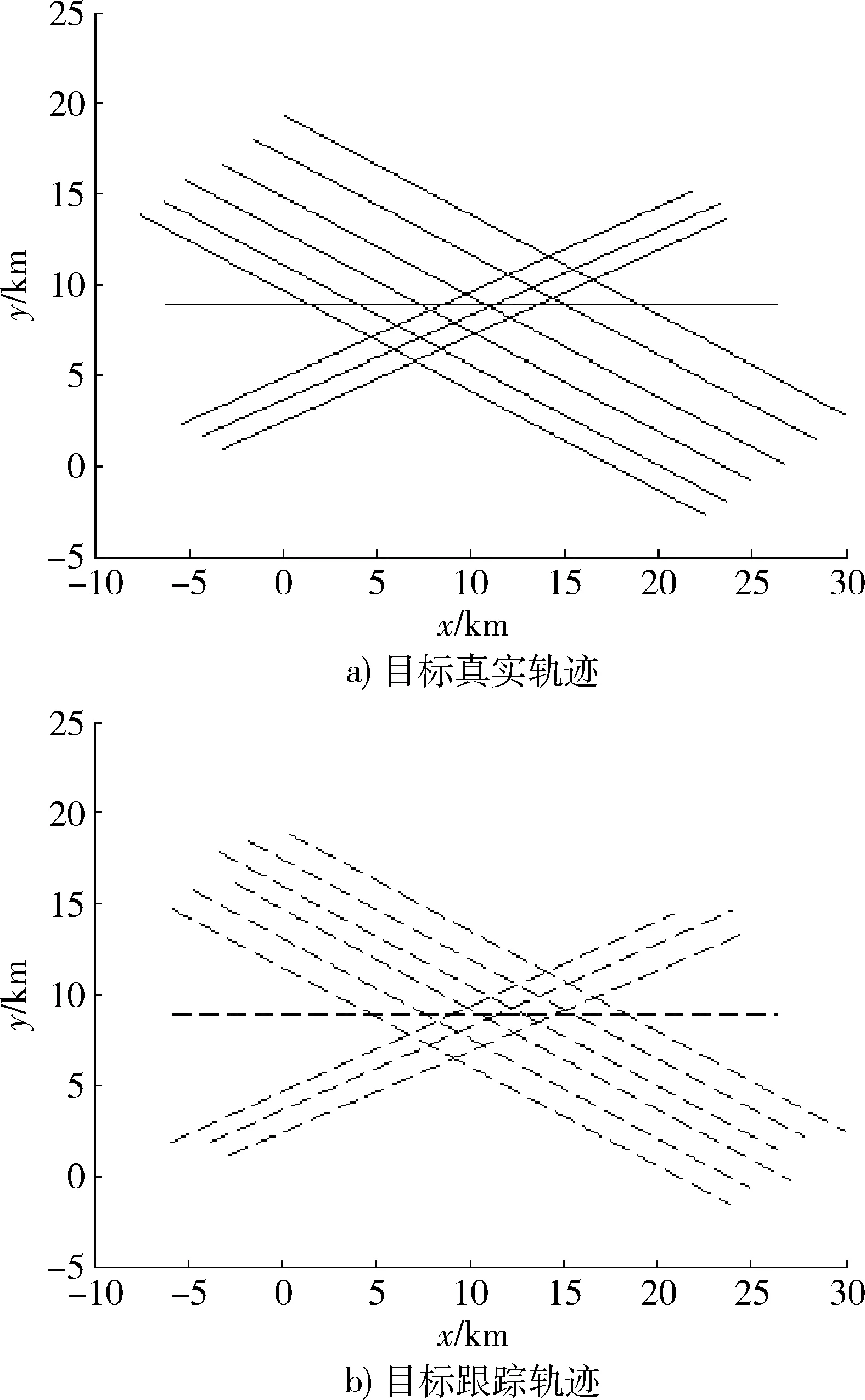
图3 目标真实和目标跟踪轨迹Fig.3 Target real trajectory and target tracking trajectory

图4给出了本文所提聚类算法的目标定位算法仿真对比图。图4表明，雷达系统采用本文所提采集数据聚类算法对空中目标进行定位追踪时，传统的滤波跟踪算法与目标真实航迹偏差较大，而采用本文的模糊数据聚类算法对空中目标进行定位时的精度较高，对于较大范围的空中目标进行定位预测时较传统的滤波跟踪算法的精度要高出很多，更加贴近空中目标真实航迹，而对于密度较大的目标群，本文所提模糊聚类算法更加精确的对目标进行预测定位跟踪。

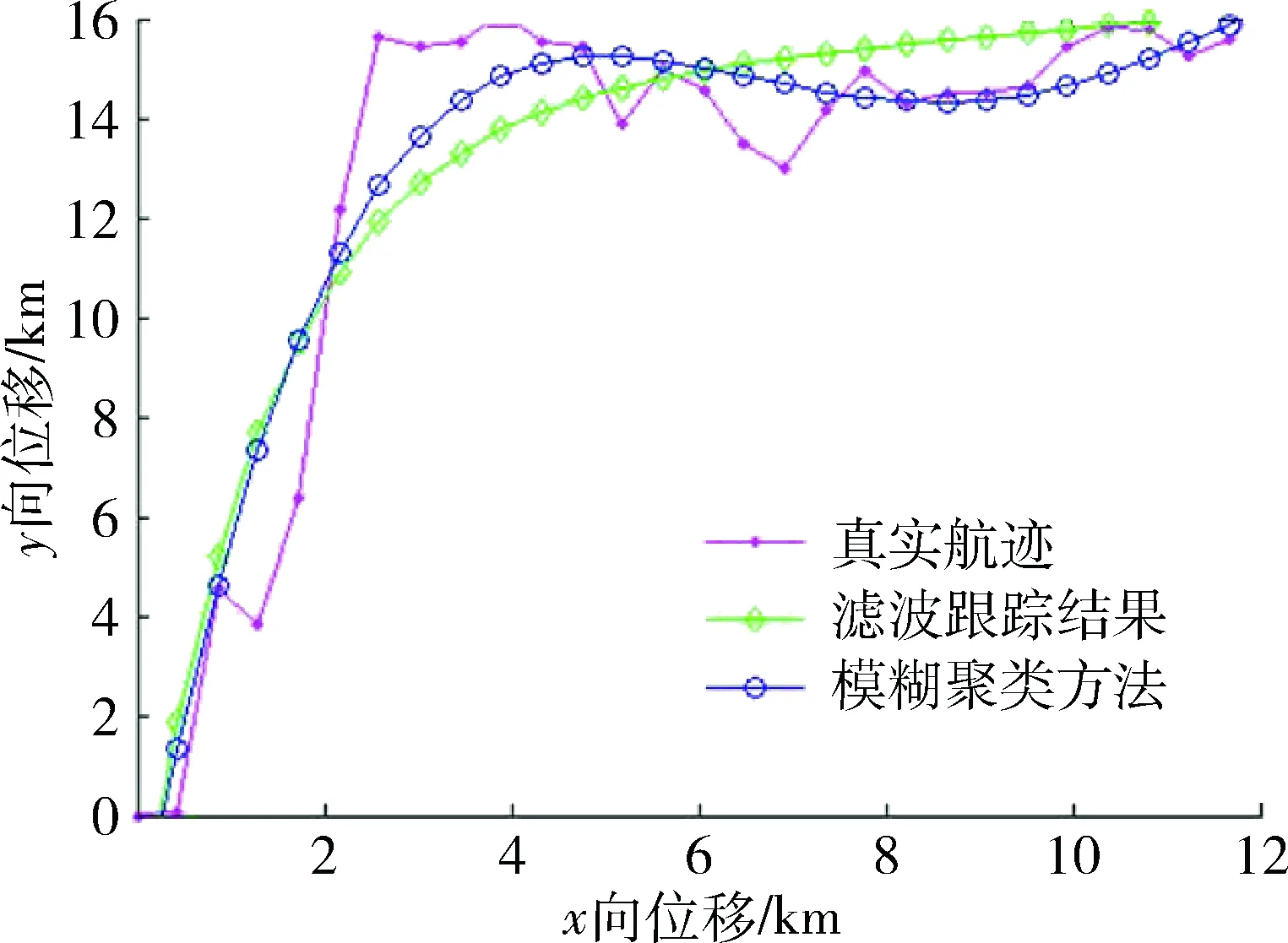
图4 雷达跟踪算法的跟踪效果对比Fig.4 Tracking effect comparison of radar tracking algorithm in multisite radar

图4表明在实际的雷达航迹测量过程中，只要设定某一合理的门限因子，就可以得到较好的追踪效果。使用链路预算分析来确定检测门限的方法对航迹探测准确率具有较高的探测精度，所以在门限因子确定后如何应用门限检测方法，具有较高的探测航迹准确度。

综上所述，基于模糊聚类算法对雷达系统中的定位具有较高的精度，其计算时间较之传统滤波跟踪算法相差不大，因此可以在雷达系统对目标定位追踪等领域进行大规模应用。

3 结束语

本文基于模糊聚类算法对雷达定位技术中的多目标数据关联进行了仿真研究，首先介绍了模糊聚类算法的原理并建立模型，通过设定的空中被测目标的位置，分别采用传统滤波跟踪算法以及本文所提算法对其进行定位跟踪，并且将二者定位跟踪结果与目标实际航迹进行对比分析，结果表明本文所提算法较传统的滤波跟踪算法精度较高，并且由于算法本身特性，其计算量亦较小，因此，现代作战中的雷达系统采用模糊聚类算法对空中目标进行精确定位是较为可行的，并且可以较为精确的反映出实时特性。

[1] PULFORS W G.Data Fusion of Multi-Radar System by Using Gene Tic Algorithm[J].IEEE Trans on Aerospace and Electronic System，2002，38(2)：601-611.

[2] 徐欣，周一宇，卢启中.雷达截获系统实时信号分选处理技术研究[J].系统工程与电子技术，2001，23(3)：12-15.

XU Xin，ZHOU Yi-yu，LU Qi-zhong.Research on Real Time Deinter Leaving Technology for Radar Intercept System[J].Systems Engineering and Electronics，2001，23(3)：12-15.

[3] Kenichi Nishiguchi，Masaaki Kobayashi.Improved Algorithm for Estimating Pulse Repetition Intervals[J].IEEE Transactions on Aerospace and Electronic Systems，2000，36(3)，497-421.

[4] Stormon Charles D.An Associative Processor Architecture and Application[M].The Coherent Processor Technical Manual.Coherent Research Inc.，1991.

[5] KENNEDY J，BEERNAERT R.Particle Swarm Optimization[C]∥Proceedings of IEEE International Conference on Neutral Networks.Perth，Australia：IEEE，1995：1942-1948.

[6] LEWIS J T，P FISTER C E.Thermodynamic Probability Theory：Some Aspects of Large Deviations[J].Russian Math.Surveys，1995，50(2)：279-317.

[7] SHANNON C E.A Mathematical Theory of Communication (Part I)[J].Bell Syst.Tech.J.1948(27)：379-423.

[8] CHANG C S，THOMAS J A.Effective Bandwidth in High-Speed Digital Networks[J].IEEE JSAC，1995，13(6)：1091-1100.

[9] CHANG C S，CHIU Y M，SONG T W.On the Performance of Multiplexing Independent Regulated Inputs[J].ACM SIGMETRICS Performance Evaluation Review，2001，29(1)：184-193.

[10] 王石记，司锡才.雷达信号分选新算法研究[J ].系统工程与电子技术，2003，25 (9)：1079-1083.

WANG Shi-ji，SI Xi-cai.Research on an Improved Sorting Method for Radar Signal[J].Systems Engineering and Electronics，2003，25(9)：1079-1083.

[11] Seong Taek Park，JANG G，YU Lee.Improved Kalman Filter Design for Three-Dimensional Radatracking[J].IEEE Transactions on Aerospace and Electronic Systems，2001，37(2)：727-739.

[12] HOLLANDS P.Use of Simulation Methods as a Design Tool in the Developments of an ESM Processing System[J ].IEE Proc，1985，24(4):292-297.

[13] 张振千，胡明宝，孟鑫，等.门限设置对雷达数据质量的影响研究[J].雷达科学与技术，2015，13(5)：491-492.

ZHANG Zhen-qian，HU Ming-bao，MENG Xin，et al.Improving the Quality of Weather Radar Data Using Threshold[J].Radar Science and Technology，2015，13(5)：491-492.

[14] 李国万，索继东，柳晓鸣.基于门限体积最小准则的认知雷达波形选择方法研究[J].网络与通信，2015(9)：62-64.

LI Guo-wan，SUO Ji-dong，LIU Xiao-ming.Research on the Selection Method of Cognitive Radar Waveforms Based on the Minization of Criterion Gate Volume[J].Network and Communication，2015(9)：62-64.

[15] 张大海，刘向阳，李华.基于满意度门限检测的多雷达航迹对提取研究[J].舰船电子工程，2011，31(7)：67-68.

ZHANG Da-hai，LIU Xiang-yang，LI Hua.Study on Track Extracting of Multi-Radar Based on Threshold Checking of Satisfactory Degree[J].Ship Electronic Engineering，2011，31(7)：67-68.