高超声速飞行器俯冲段制导控制方法研究*
2018-01-02刘清楷陈坚汪立新秦伟伟张广豪
刘清楷,陈坚,汪立新,秦伟伟,张广豪
(火箭军工程大学,陕西 西安 710025)
0 引言
高超声速飞行器由于其飞行速度快、机动能力强等特点,具有较高的军事和民用价值[1],成为国内外研究热点,但其具有的复杂气动模型,使其呈现出强非线性、快时变和强耦合性等特点,为制导控制系统设计带来了极大的挑战[2]。
俯冲段作为高超飞行器攻击目标的最后一个阶段,事关飞行任务的成败。现有文献对俯冲段制导与控制问题做了多方面研究,成功将最优控制[3],滑模控制[4],反演法[5],动态逆[6]等非线性控制方法,以及Fuzzy控制[7]、预测控制[8]和神经网络[9]等现代控制方法应用到其中。但目前已有的研究大多是针对制导或控制问题中某一方面进行研究,本文则进行制导控制回路的综合设计。
传统导弹制导控制回路设计常采用分离理论[10],忽略制导与控制回路之间的耦合,分别独立进行两个回路的设计工作,在制导回路设计时一般不包含弹体的姿态、转速等状态信息,在弹目相对运动速度较大时,产生的制导指令容易超出控制回路的性能限制。同时,控制回路的设计也未涉及到导弹与目标之间的位置和速度信息,因此无法根据和目标的相对距离而调整自身的响应速度。这种结构在弹目相对运动速度不是特别大的情况下是可以满足应用要求的,但由于高超声速飞行器的速度快,这种结构就难以适用。制导控制一体化(integrated guidance and control,IGC)方法使用一个回路完成制导与控制,简化了回路设计,充分运用了状态信息,然而由于制导与控制回路变量间存在固有的时间常数差距,比较理想化,不利于工程应用。在飞行器进行高速机动时,可能会造成控制失稳乃至发散的情况出现,这是由于在使用舵面进行控制时,所产生的控制力矩要远大于所产生的控制力,在产生满足制导要求的控制力的情况时,就可能造成姿态失稳。而本文所采用的回路结构,综合了IGC单回路和传统方法的特点,既综合利用弹目相对运动信息和机体角速度等状态信息,同时又兼顾了变量间时间常数的差别,同时与IGC采用单回路相比,还可以避免状态量的高阶导数的出现。本文根据弹目相对运动的信息,结合高超声速飞行器六自由度模型,通过计算得到所需的外环角速度指令表达式,采用滑模控制方法进行跟踪,得到所需的舵偏角指令信号。本文尝试建立高超声速飞行器的六自由度模型,直接利用文献[11]所给GHV(generic hypersonic vehicle)模型,而不进行一般文献所做的面向控制的模型简化。
1 模型描述
1.1 高超声速飞行器六自由度模型
由于高超声速飞行器俯冲段飞行距离短,故考虑在大地为平面的假设下,在机体坐标系建立高超声速飞行器的六自由度模型[12]。
(1)
式中:Fx=Lsinα-Ncosαsinβ-Dcosαcosβ;Fy=Lcosα+Nsinαsinβ+Dsinαcosβ;Fz=Ncosβ-Dsinβ;u,v,w为高超声速飞行器速度在机体系的分量;m为高超声速飞行器质量;g为重力加速度;α,β为攻角和侧滑角;D,L,N为气动阻力;Ixx,Iyy,Izz为飞行器转动惯量;lx,ly,lz分别为滚动、偏航和俯仰通道气动参考长度。
气动阻力、气动升力以及气动侧向力具体表达式为
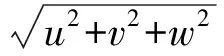
由于采用了GHV模型,这里有lx=ly=a,lz=c,且a,c分别为飞行器横向气动参考长度和纵向气动参考长度;ωx,ωy,ωz为机体角速度在机体系的分量;t12,t22,t32为矩阵TBI的元素,TBI为用四元数q0,q1,q2,q3表示的惯性系到机体系的变换矩阵。四元数的更新公式[13]为
(2)
式中:
高超声速飞行器的质心运动方程为
(3)
式中:xg,yg,zg为飞行器质心位置在地面惯性系中的分量。
本文将利用式(1)的六自由度方程和式(3)进行制导控制系统的设计,并利用其进行数字仿真验证。
1.2 三维弹目相对运动模型
本文基于零化视线角速率原理生成外环控制指令,图1给出了飞行器与目标相对运动的关系。首先建立地面目标与高超声速飞行器的相对运动模型[14]为
(4)


图1 飞行器与目标相对运动关系示意图Fig.1 Geometry of relationship between vehicle and target
2 制导控制回路设计
前面已经提到了不完全制导控制一体化方法的主要思想,图2给出了内外回路的结构关系。首先由外环根据相对距离信息给出所期望的角速度作为中间控制量,在由内环跟踪这个中间控制量得到最终的舵偏角控制量,这一过程通过解析的运算,不会出现由于集成度的增加而造成过控的情形出现。下面就分别对2个回路进行设计。
2.1 外环设计
前面给出了飞行器的六自由度运动模型,对式(3)进行求导,整理可得
(5)
式中:
将式(2)代入式(5)得到:

(6)

m11=2(q0q3-q1q2)v+2(q0q2+q1q3)w;
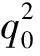
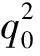
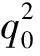
m22=2(q0q1-q2q3)u+2(q0q3+q1q2)w;
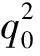
m33=2(q0q1+q2q3)u+2(q0q2-q1q3)v.
由式(4)可得
(7)
式中:
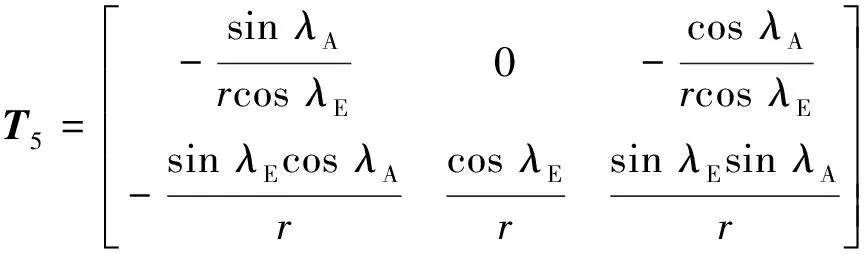
为满足视线角速率为0的要求,设计滑模面向量为
.
(8)
取如下的终端滑模到达律:
(9)
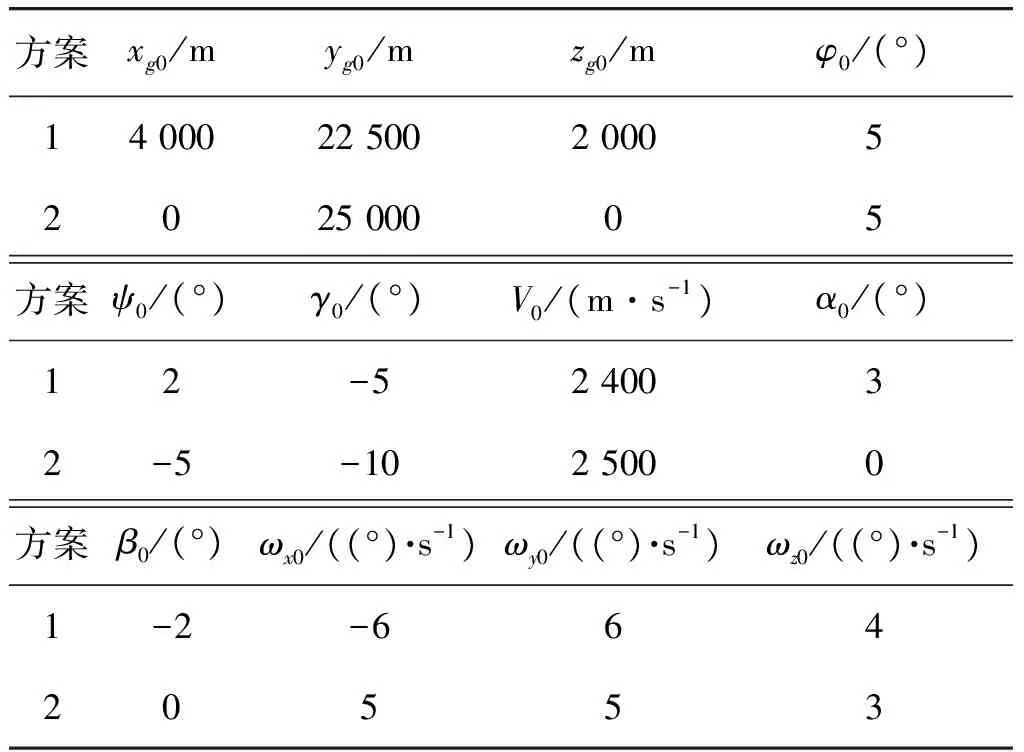
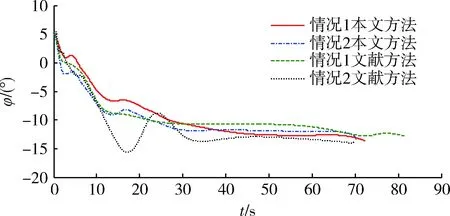
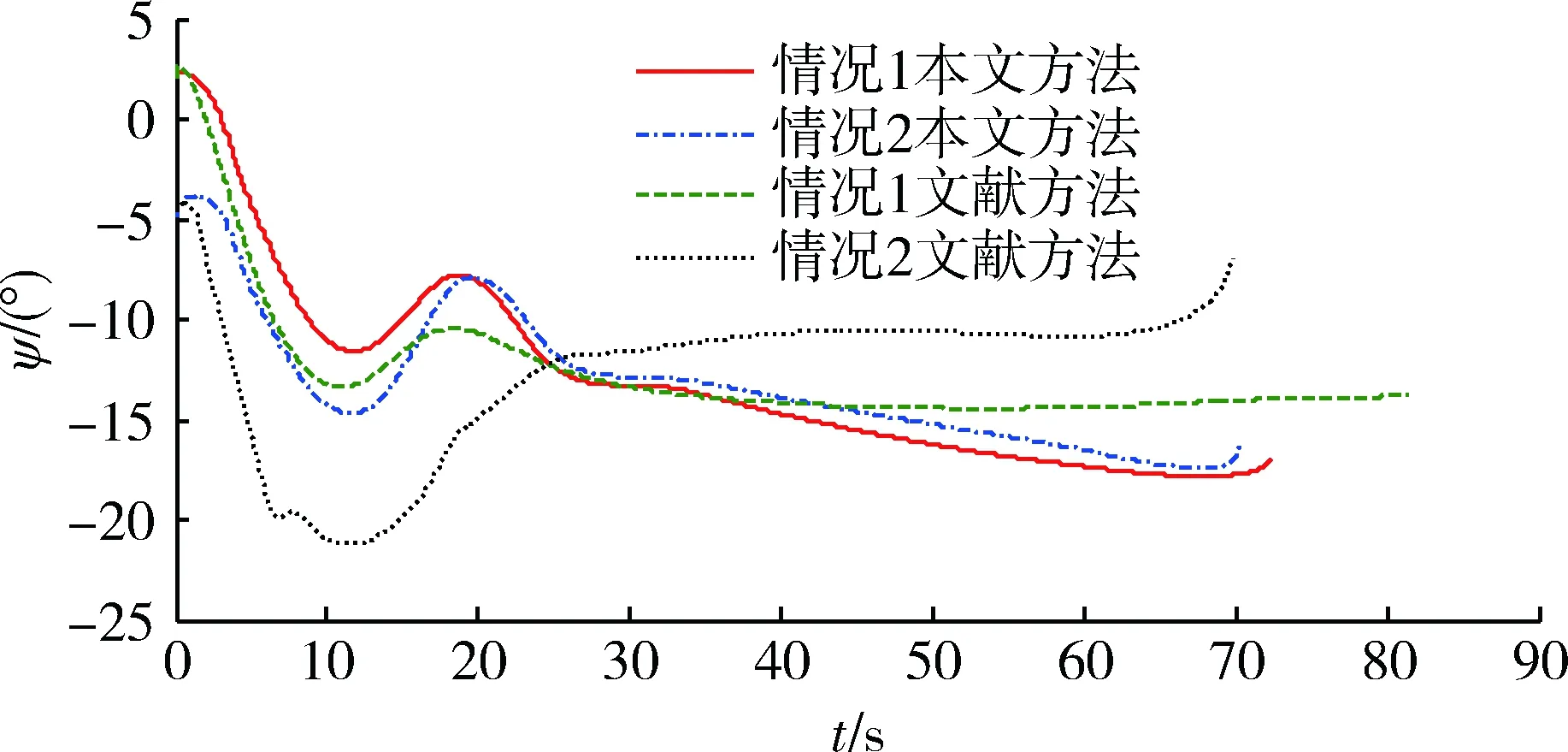
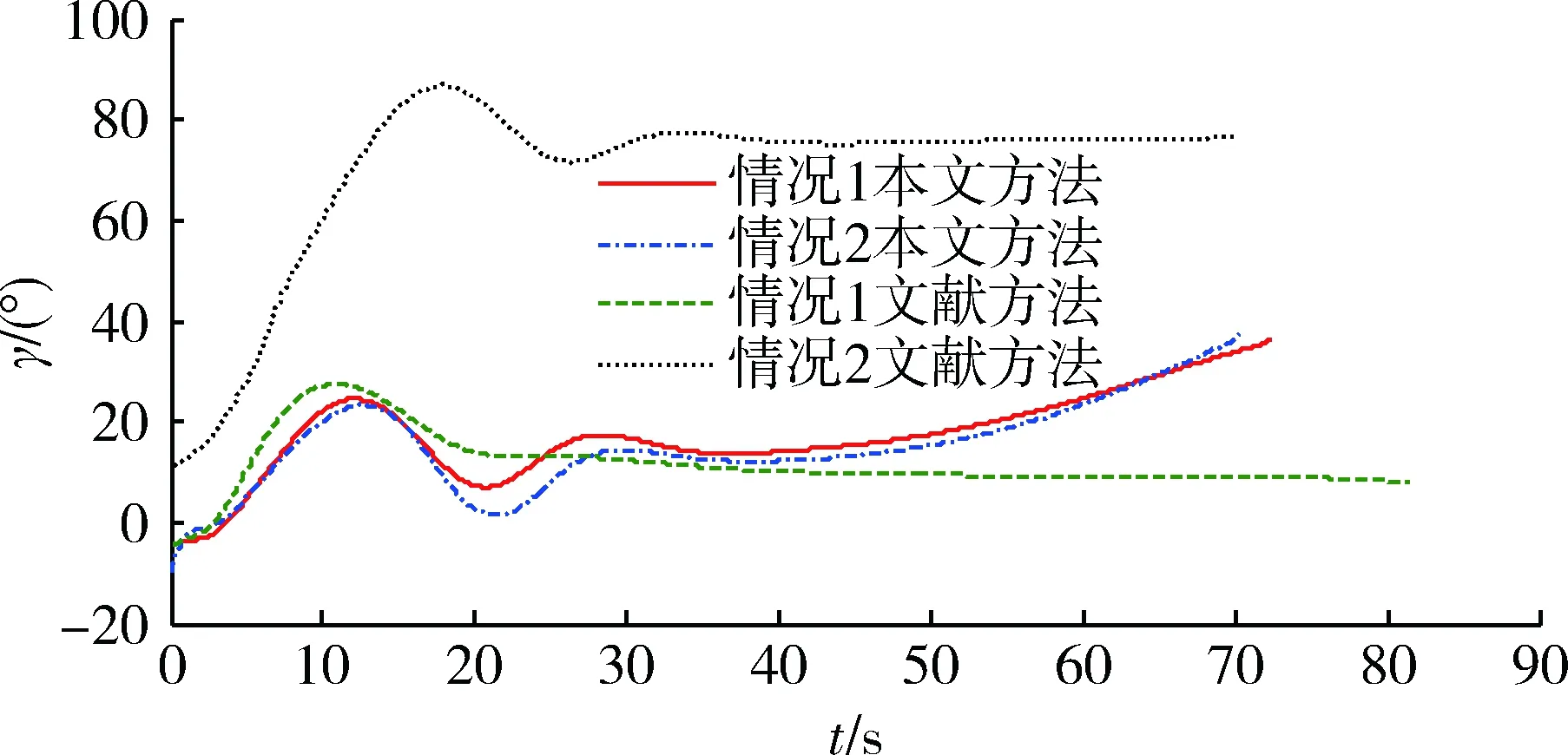
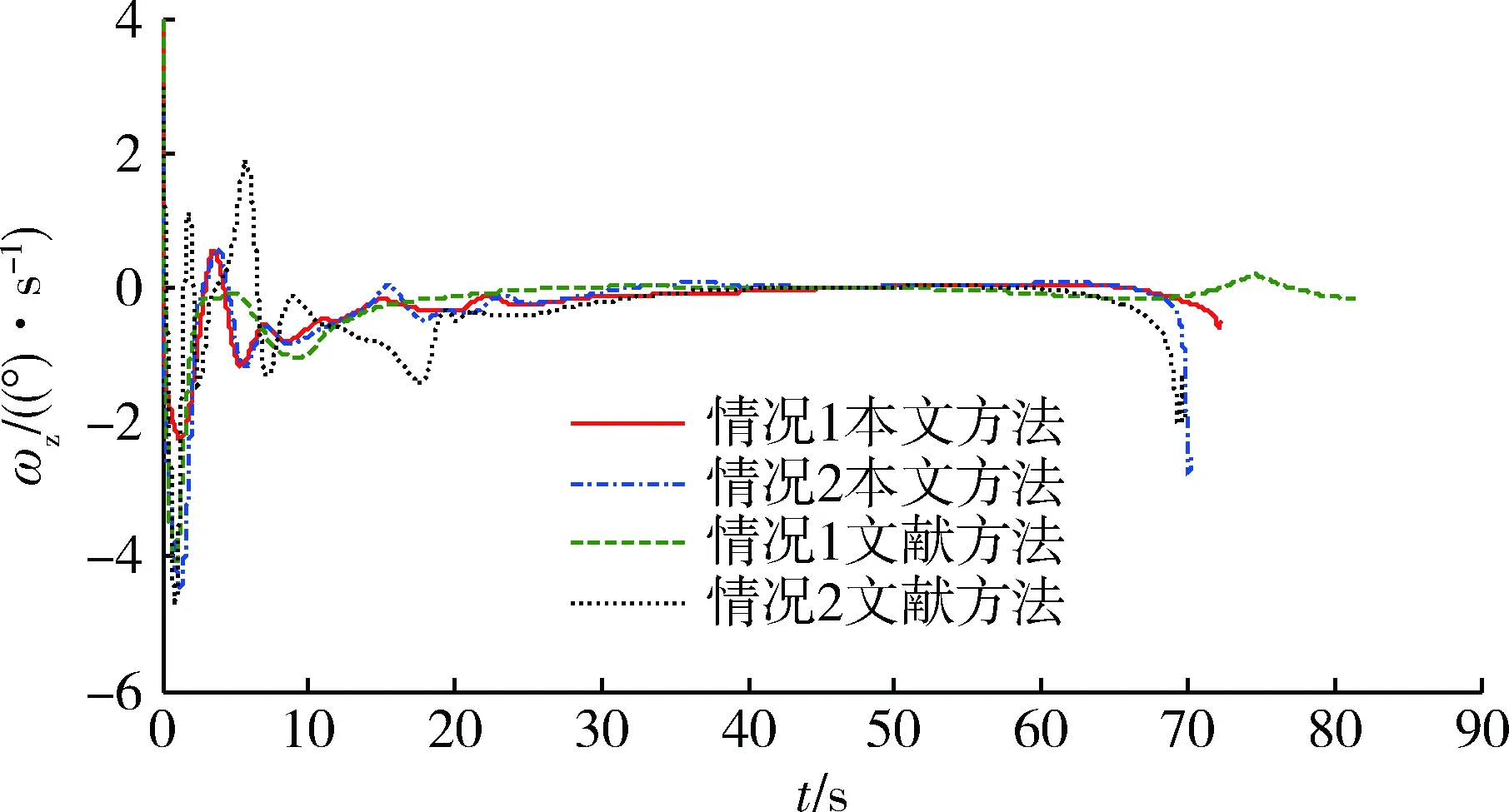
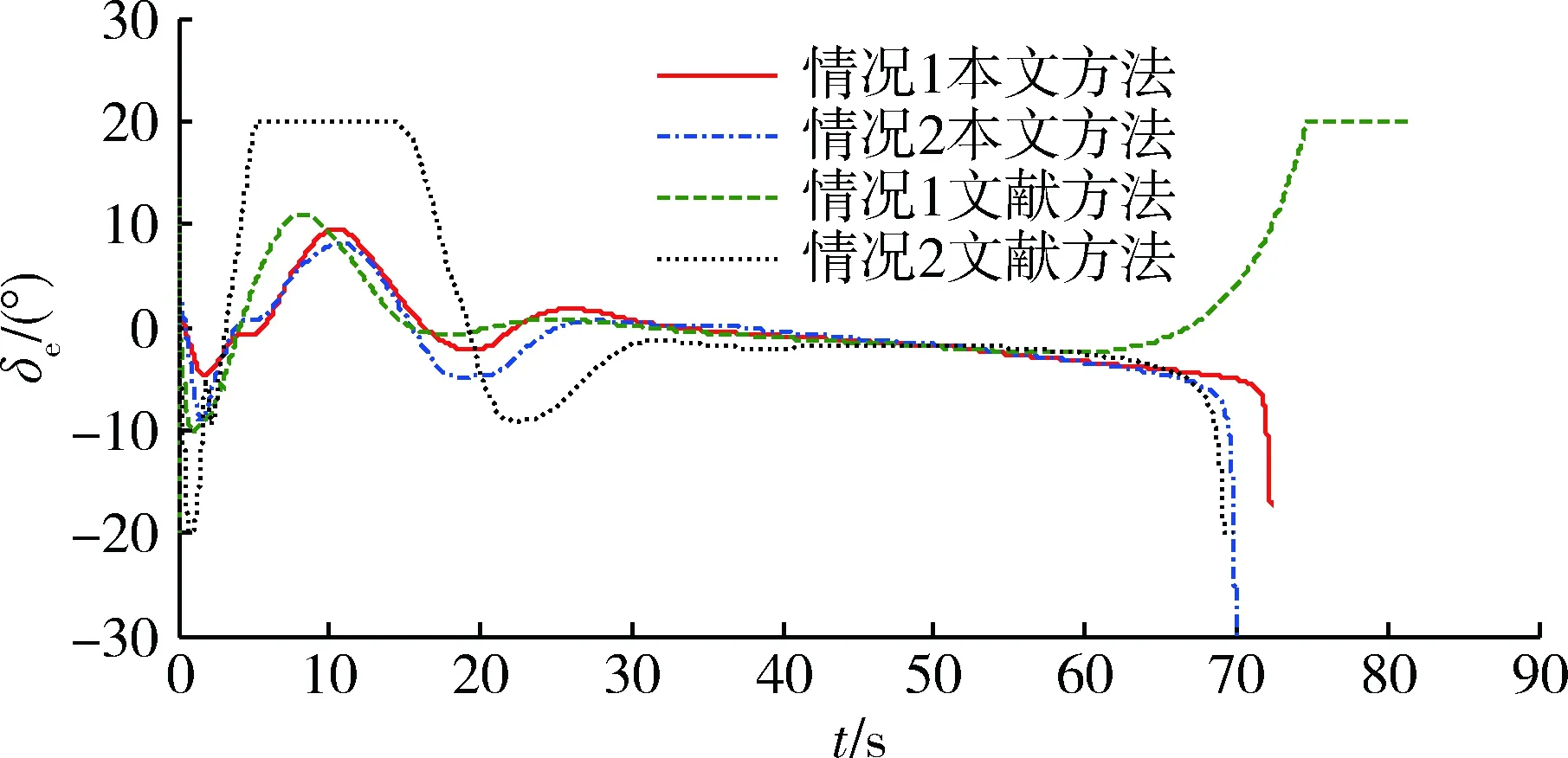
式中:k11,k12∈R2×2;0 将式(8)求导得到: 将式(6)代入上式得 . (10) 通过式(10)即可获得满足飞行器准确命中目标要求的角速率信号,将其作为外环虚拟控制量送入内环。下面设计内环通过跟踪该虚拟控制量来产生飞行器的舵偏指令信号。 将式(1)作以下变形: (11) 图2 回路结构关系示意图Fig.2 Structure relationship between the outer and inner loops 式中:ΔCl,ΔCn,ΔCm为除去舵偏一次相关项系数剩余的气动力矩系数。 为跟踪外环得到的角速率控制信号,设计滑模面为 (12) 同时采用如下滑模到达律: (13) 式中:k21,k22∈R3×3为待设计反馈系数。 由式(10)可得期望的舵偏角指令为 . (14) 考虑实际舵机执行机构的动态过程,将舵偏角指令通过下面的二阶惯性环节,得到的输出作为仿真时的舵偏角为 (15) 式中:ωn=20 Hz为执行机构自然频率;ξ=0.7为阻尼比。 设置偏角幅值范围为(-25°,25°),偏角速率范围为(-100,100)(°)/s。 为了减小滑模控制的抖振,采用饱和函数来替代符号函数。 本文基于大部分已有文献所采用的Langley发布的GHV模型进行仿真验证。为了验证本文所推导方法的有效性,通过设置飞行器不同初始条件,进行仿真,同时采用文献[15]的IGC方法,(以下简称文献)在相同条件下进行仿真,观察仿真结果。 仿真所需的初始仿真条件以及所设计的一些参数值如表1所示。 表1 飞行参数初始值Table 1 Initial value of the flight 四元数初始值(q00,q10,q20,q30)T由下式求得,式中φ0,ψ0,γ0分别为飞行器初始俯仰角,偏航角,滚动角。 (q00,q10,q20,q30)T= 速度分量初始值 可由下式计算得到: 式中: . 飞行器基本参数如表2所示。 设定目标位置坐标为:xt=150 000 m,yt=0 m,zt=30 000 m;文中所设计的参数:d1=d2=0.6,k11=diag(0.015,0.02),k12=diag(0.005,0.005),k21=diag(1.5,1.5),k22=diag(0.001 5,0.001 5)。 仿真结果如图3~13所示。这里说明在图10~12中舵偏角在最后时刻出现了迅速增加的情形,这是由于直接使用弹目相对运动信息,本文的处理方法与文献[12]中一致。 图3 飞行器在三维空间运动轨迹图Fig.3 Trajectories of the vehicle in 3D space 图4 俯仰角变化图Fig.4 Curves of the pitch angle 为检验本文提出的制导控制方法的鲁棒性,图13给出了Monte Carlo法仿真得到的脱靶量散点图;在仿真时,对飞行器的质量和转动惯量的标称值上加入相当于标称值15%的高斯随机噪声,其余条件与情况一保持一致,最终其脱靶量均值为6.312 m,均方差为1.532 m,可以看出本文方法具有一定的鲁棒性。 通过仿真可以看出高超声速飞行器能够以3.484 m的精度命中目标,文献[15]的精度为6.562 m,使用本文方法提高了命中精度,并且飞行器在飞行过程中的状态量和舵偏角变化相比文献[15]更加平稳。可以看到飞行器飞行过程中,各项状态变化平稳,这得益于跟踪角速度来产生控制指令,这种思想类似于积分滑模减小抖振的原理。 图5 偏航角变化图Fig.5 Curves of the yaw angle 图6 滚动角变化图Fig.6 Curves of the roll angle 图7 俯仰角速率变化图Fig.7 Curves of the pitch angle rates 表2 GHV基本参数Table 2 Basic parameters of the GHV 图8 偏航角速率变化图Fig.8 Curves of the yaw angle rates 图10 左侧升降舵舵偏变化图Fig.10 Curves of the left elevon deflections 图11 右侧升降舵舵偏变化图Fig.11 Curves of the right elevon deflections 图12 方向舵舵偏变化图Fig.12 Curves of the rudder deflections 图13 脱靶量散点图Fig.13 Miss distance scatter diagram 针对高超声速飞行器的制导与控制问题,建立了基于四元数的高超声速飞行器的六自由度模型,避免了高超声速飞行器在大机动飞行时,欧拉角解算存在的发散问题;利用三维弹-目模型,未进行横纵向平面的解耦,更加符合高超声速进行大范围机动的特点,充分利用了相对运动信息,使高超声速飞行器在高速度飞行过程中保持平稳可控,有效完成目标打击任务。通过Monte Carlo法验证了本文方法具有一定的鲁棒性,综合仿真的结果来看本文方法具有一定的理论意义,但在制导信息中存在噪声的情况还考虑不足,可以作为下一步的研究方向。 [1] 孙长银,穆朝絮,余瑶.近空间高超声速飞行器控制的几个科学问题研究[J].自动化学报,2013,39(11):1901-1913. SUN Chang-yin,MU Chao-xu,YU Yao.Some Control Problems for Near Space Hypersonic Vehicles[J].AcTa Automatica Sinica,2013,39 (11):1901-1913. [2] 李惠峰.高超声速飞行器制导与控制技术[M].北京:中国宇航出版社,2012:242-243. LI Hui-feng.Guidance and Control Technology of Hypersonic Vehicles[M].Beijing:China Astronautic Publishing House,2012:242-243. [3] ZHU J W,LIU L H,TANG G J,et al.Highly Constrained Optimal Gliding Guidance[J].Journal of Aerospace Engineering,2015,229(12):2321-2335. [4] 朱建文,刘鲁华,汤国建,等.基于反馈线性化及滑模控制的俯冲机动制导方法[J].国防科技大学学报,2014,36(2):24-29. ZHU Jian-wen,LIU Lu-hua,TANG Guo-jian,et al.Diving Guidance with Maneuver Based on Feedback Linearization and Slide Mode Control[J].Journal of National University of Defense Technology,36(2):24-29. [5] 宋超,赵国荣,盖俊峰.基于非线性干扰观测器的高超声速飞行器反演滑模控制[J].系统工程与电子技术,2012,34(6):1231-1234. SONG Chao,ZHAO Guo-rong,GAI Jun-feng.Sliding Mode Backstepping Control for Hypersonic Aircraft Based on Nonlinear Disturbance Observer[J].Systems Engineering and Electronics,2012,34( 6):1231-1234. [6] 曾宪法,王小虎,张晶,等.高超声速飞行器的干扰补偿Terminal滑模控制[J].北京航空航天大学学报,2012,38(11):1454-1458. ZENG Xian-fa,WANG Xiao-hu,ZHANG Jing,et al.Disturbance Compensated Terminal Sliding Mode Control for Hypersonic Vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(11):1454-1458. [7] HU X,WU L,HU C,et al.Fuzzy Guaranteed Cost Tracking Control for a Flexible Air-Breathing Hypersonic Vehicle[J].Iet Control Theory & Applications,2012,6(9):1238-1249. [8] ZHANG T,ZHOU J,GUO J.Design of Predictive Controller for Hypersonic Vehicles Based on Disturbance Observer[J].Acta Aeronautica Et Astronautica Sinica,2014,35(1):215-222. [9] XU B,SHI Z K,YANG C G,et al.Neural Control of Hypersonic Flight Vehicle Model Via Time-Scale Decomposition with Throttle Setting Constraint[J].Nonlinear Dynamics,2013,73(3):1849-1861. [10] 赵善友.防空导弹武器寻的制导控制系统设计[M].北京:宇航出版社,1992:136-140. ZHAO Shan-you.Homing Guidance and Control System Design for Air Defense Missiles[M].Beijing:China Astronautics Publishing House,1992:136-140. [11] KESHMIRI S,MIRMIRANI M,COLGREN R.Six-DOF Modeling and Simulation of a Generic Hypersonic Vehicle for Conceptual Design Studies[C]∥AIAA Modeling and Simulation Technologies Conference and Exhibit,Rhode Island,August 16-19,2004. [12] 赵汉元.飞行器再入动力学与制导[M].长沙:国防科技大学出版社,1997:56-64. ZHAO Han-yuan.Spacecraft Reentry Dynamics & Guidance[M].Changsha:Press of National University of Defense Technology,1997:56-64. [13] 秦丽,张文栋,潘峰.大攻角飞行载体运动学建模的四元数方法研究[J].中北大学学报:自然科学版,2006,27(3):276-279. QIN Li,ZHANG Wen-dong,PAN Feng.Quaternion Method for Kinematics Modeling of High Attack Angle Flying Carrier[J].Journal of North University of China:Natural Science ed,2006,27(3):276-279. [14] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002:14-16,30-31. ZHOU Di.New Guidance Laws for Homing Missile[M].Beijing:National Defense Industry Press,2002:14-16,30-31. [15] 王建华,刘鲁华,王鹏,等.高超声速飞行器俯冲段制导控制一体化设计方法[J/OL].航空学报.(2016-08-17)[2017-01-02].http://www.cnki.net/kcms/detail/11.1929.V.20160817.1424.002.html. WANG Jian-hua,LIU Lu-hua,WANG Peng,et al.Integrated Guidance and Control Scheme for Hypersonic Vehicles in Dive Phase[J/OL].Acta Aeronautica et Astronautica Sinica. (2016-08-17)[2017-01-02].http://www.cnki.net/kcms/detail/ 11.1929.V.20160817.1424.002.html.
2.2 内环设计

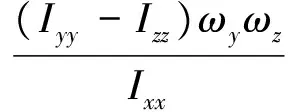


3 仿真校验
3.1 仿真条件及参数
3.2 仿真结果






4 结束语
