利用反步控制法的带角度约束制导律研究*

曹有亮

(中国空空导弹研究院，河南 洛阳 471009)

0 引言

最近几十年新型制导炸弹层出不穷，而新型制导炸弹的现代化程度越来越多地体现在制导方面。

要想提高炸弹的侵彻深度和杀伤效果，就需要炸弹以大落角击中目标，最好能够达到垂直攻击[1]。因此，适用于制导炸弹的带落角约束的制导律研究成为近年来的一个研究热点。 一部分学者以变结构理论为基础，通过滑模面中加入落角约束项来设计带落角约束制导律，这种制导律能够很好的满足设计要求，但是存在控制量抖动问题[2]；还有一部分学者以落地速度倾角作为终端约束，以脱靶量、最小能量消耗为性能指标，给出了一种适用于攻击地面目标的最优制导律，同时满足了精度和角度的要求[3]。但是，以上这些的制导律设计中的目标模型都是固定的目标，或者是二维运动的，都不适合模拟未来将会出现的很多地面高速目标的运动。

基于此，本文首先建立一个三维弹目运动模型，然后利用反步控制方法[4]，研究了一种适用于攻击运动目标的三维带落角约束制导律。

1 三维弹目运动方程

制导律的研究时，可对弹目动力学特性进行简化，然后基于弹目三维运动学特性进行设计。因此在建立弹目运动学方程前，可首先做如下假设：①导弹和目标在惯性坐标系中，均可认为是质点；②导弹稳定回路和制导信息获取过程的动态特性足够快，与制导回路相比可以忽略；③导弹和目标的攻角很小，可以认为弹道坐标系和弹体坐标是重合的；④导弹和目标的速度是常值，这样导弹和目标的机动加速度就可以通过弹目的法向加速度来表示[5]。

导弹目标的相对运动如图1所示。

图1 导弹和目标的运动关系Fig.1 Kinematic relation between missile and target

图1中，x,y,z为惯性静坐标系；xL,yL,zL为视线动坐标系；T代表目标；M代表导弹；qε,qβ分别代表视线的俯仰角和方位角；R为弹目距离；vt，vm分别为目标和导弹的速度；aMr,aMε,aMβ为导弹加速度在视线坐标系3个轴上的分量；aTr,aTε,aTβ为目标加速度在视线坐标系3个轴上的分量。

弹目相对速度矢量在视线坐标系3个轴上的分量为

(1)

根据速度矢量的绝对导数与相对导数(由动静坐标系中质点的牵连运动引起)之间的关系有

(2)

则

(3)

下面先给出惯性坐标系到视线坐标系的变换矩阵：

(4)

(5)

将式(5)与速度向量相乘，有

(6)

将式(6)代入式(2)，可得

(7)

从式(7)中可以看到，视线的俯仰和偏航通道存在严重的交叉耦合。因此就需要研究一种新型制导律来处理这种耦合情形，且不需要太多的观测信息，同时要结构简单，易于工程实现。

2 基于反步控制法的带落角约束制导律研究

在实际的对地攻击过程中，导弹的速度大小一般是不可知的，只通过法向过载控制导弹的速度方向。导弹和目标相对距离变化率小于0，只要控制视线角速率为0，就能确保命中。因此在制导律的推导过程中以0化视线角速率为目标，可以不考虑式(7)中的第1项[6]。

(8)

对于以上非线性反馈控制系统，运用反步控制方法，选取第1步李亚普诺夫函数V1[8]为

(9)

式中:P>0；tgo为剩余时间;x1为落角误差，此函数收敛，就可以保证实际落角与期望落角之间的误差收敛为0。

式(9)对时间求导，且知dtgo/dt=-1，可得

(10)

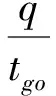
(11)

式中：q>1。

对于整个系统来说，可以考虑如下的李亚普诺夫函数[9]：

(12)

式中:第1项是保证实际落角与期望落角之间的误差收敛到零;第2项是保证第1项收敛的条件，同时也保证了俯仰通道视线角速率的收敛;第3项是保证偏航通道视线角速率收敛为0。

对式(13)相对时间求导，可得

(13)

将式(8)代入式(13)，有

(14)

(15)

式中:g>0，整理得导弹加速度指令：

(16)

将式(16)代入式(13)，有

此时，李亚普诺夫函数为负，则系统稳定收敛到平衡状态[11]。

(17)

式中：制导律aMε的第1项和第2项是来控制导弹俯仰通道的视线稳定；第3项是约束导弹的落地角与期望落地角之间的误差；aMβ则是控制导弹偏航通道的视线稳定。由推导过程可知，p>0，q>1，k>0，制导律中参数q，k可根据此条件选择，但是参数也不能选择的过大，因为制导参数过大会放大制导信息中的误差。

3 仿真结果及分析

首先通过数字仿真来进行制导参数的拉偏，并对不同制导参数的制导特性进行对比分析，得到合适的制导参数，然后，再对末制导段进行仿真分析，验证本文制导律效果[12]。

3.1 制导参数对制导效果的影响

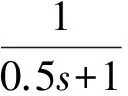
下面对落角误差系数和制导参数进行仿真分析，以得到最优的制导参数。

(1) 落角误差系数q

落角误差系数决定了落角误差约束项的大小，其取值对制导指令的大小有很大影响[14]。选取制导参数k=1，落角误差系数q分别取值1.1，1.3，1.5，1.7，2.0进行仿真。

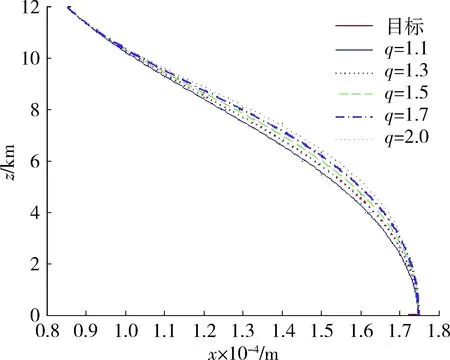
图2 俯仰通道弹道曲线Fig.2 Trajectory curve of pitch channel

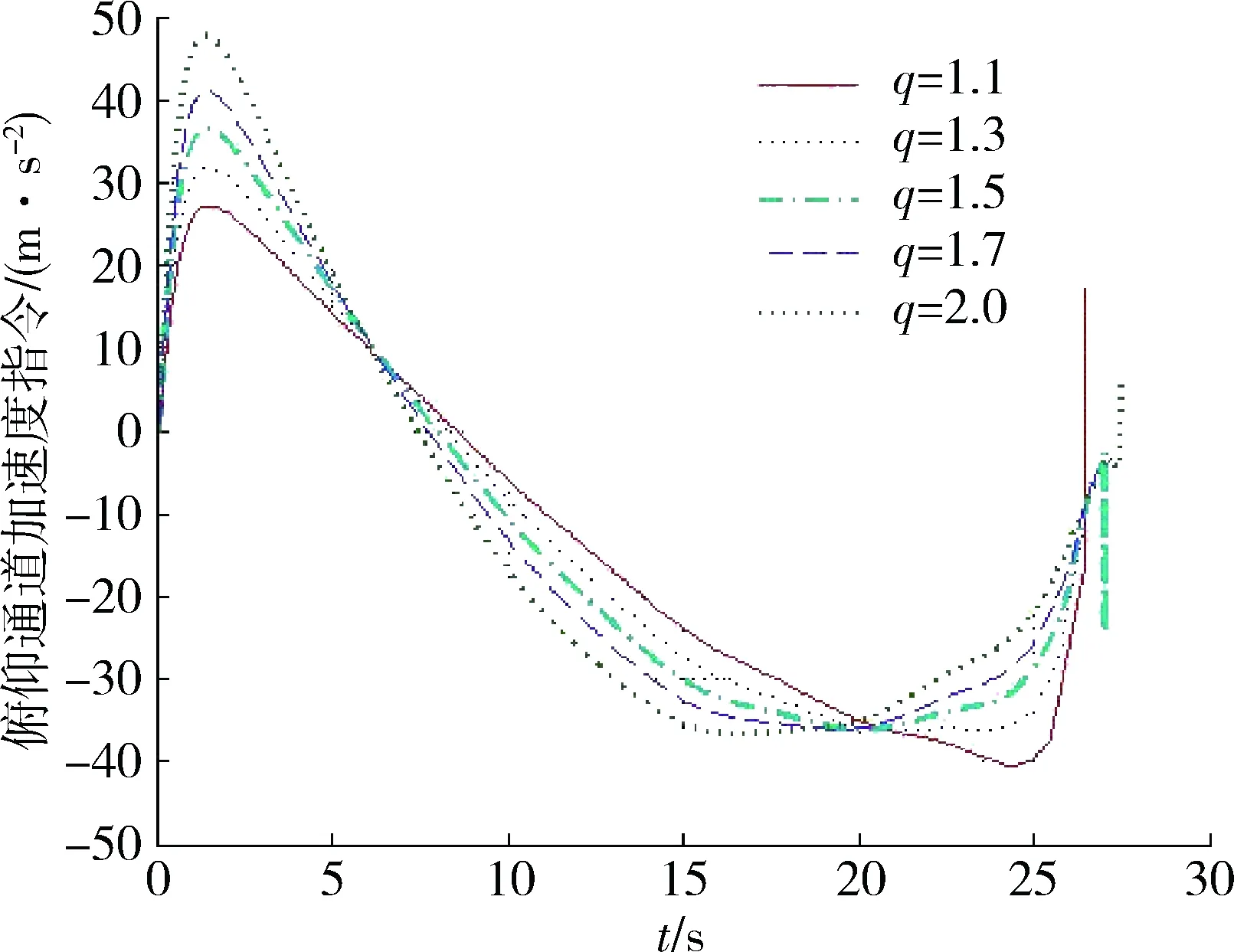
图3 俯仰通道法向加速度Fig.3 Normal acceleration of pitch channel

从图2、图3的仿真结果可以看出，当落角误差系数较大时，导弹末制导段的初始段要求的法向过载较大，这样造成加速度指令曲线弯曲程度大，不够平滑。随着落角误差系数的较小，导弹末制导段的初始段要求的法向过载逐渐变小，加速度指令曲线越来越平滑。所以，在保证落角约束能力和视线稳定要求的同时，需要对落角误差系数q的取值进行折衷，在下面的仿真中取值q=1.1。

(2) 制导参数k

制导参数k对制导律中的视线约束项有较大影响，同时对落角误差项也有一定的影响。选取制导参数q=1.1，落角误差系数k分别取值0.5，1.0，1.5，2.0，2.5进行仿真。

从图4和图5的仿真结果可以看出，制导参数k的取值过大时，导弹末制导段的初始段要求的法向过载较大，加速度曲线不够平滑，虽然此时能够保证落角约束能力和脱靶量，但同时也会放大导航误差和系统噪声。制导参数k的取值过小时，弹道末端需要的法向过载较大，同时落角约束能力也受到限制。所以，需要对制导参数k的取值进行折衷，在下面的仿真中取值k=1。

图4 俯仰通道弹道曲线Fig.4 Trajectory curve of pitch channel

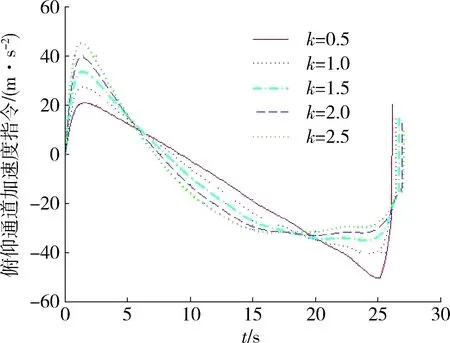
图5 俯仰通道法向加速度Fig.5 Normal acceleration og pitch channel

3.2 三自由度弹道仿真和结果分析

为了验证本文所研究的制导律的有效性，更清楚的说明基于反步控制法的落角约束制导律的性能优劣，在同一条件下引入如下带落角约束的最优制导律[15]进行仿真比较。

(18)

选取地面移动目标为攻击目标，对导弹末制导段进行仿真验证。仿真初始条件设为：导弹坐标为(6，12，6)km，目标的坐标为(12，0，12)km，导弹速度vM=600 m/s，目标速度vT=20 m/s，导弹最大机动能力为aMmax=10g。

对于本文所得的制导律，令参数q=1.1，k=1，期望落角qεf=89°，qβf=0°。令式(17)为制导律A，式(18)为制导律B，仿真结果如图6～13所示。图6为缩放图，坐标x，y，z的单位均为m。

对于侧向机动目标，目标侧向机动加速度aT=0.3g,如图6～9所示。

图6 攻击侧向机动目标的三维弹目运动轨迹Fig.6 Three-dimensional missile and target movement trajectory when attacking side-direction maneuvering target

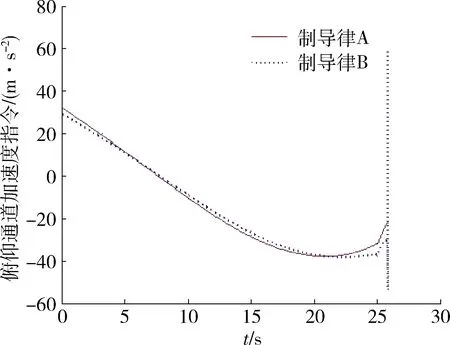
图7 俯仰通道加速度指令Fig.7 Acceleration instruction of pitch channel

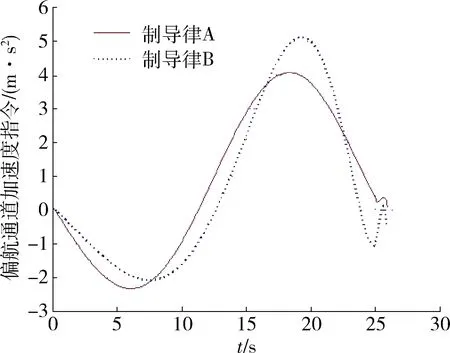
图8 偏航通道加速度指令Fig.8 Acceleration instruction of jaw channel

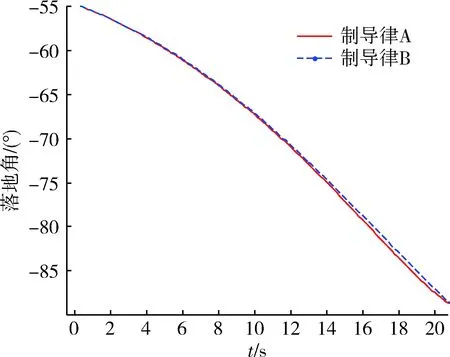
图9 落地角变化曲线Fig.9 Changing curve of landing angle

对于蛇形机动目标，目标侧向机动加速度aT=-0.5gsin(0.2 πt),如图10～13所示。图10为缩放图，坐标x，y，z的单位均为m。

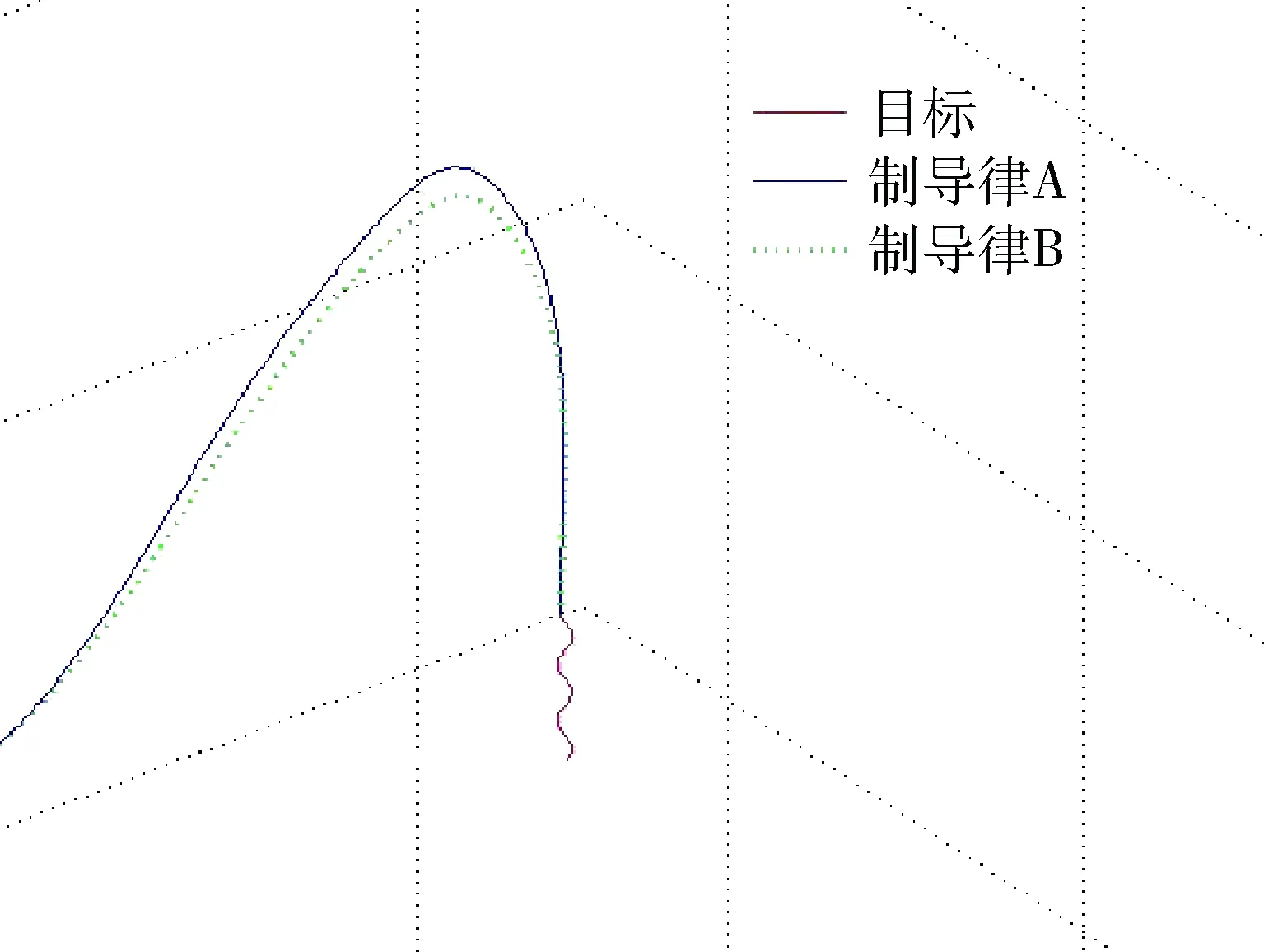
图10 攻击蛇形机动目标的三维运动轨迹Fig.10 Three-dimensional movement trajectory when attacking snake maneuvering taget

图11 俯仰通道加速度指令Fig.11 Acceleration instruction of pitch channel

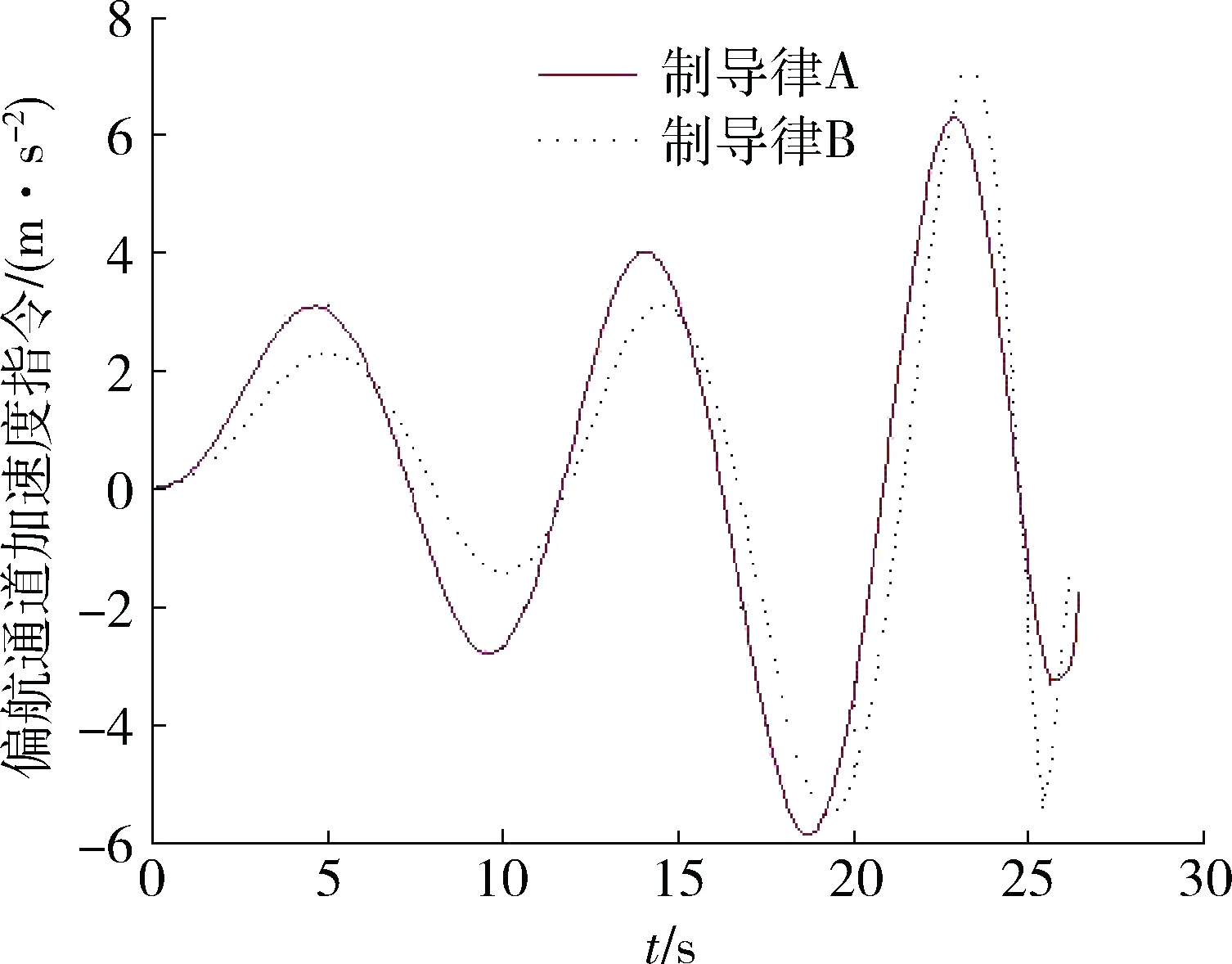
图12 偏航通道加速度指令Fig.12 Acceleration instruction of jaw channel

图13 落地角变化曲线Fig.13 Changing curve of landing angle

仿真结果表明，本文所设计的带落角约束制导律和制导律B在目标机动的情况下能准确的命中目标。从脱靶量方面看，在2种目标机动情况下，制导律A的脱靶量分别是0.19 m和0.17 m，制导律B的脱靶量分别是0.34 m和1.44 m，虽均满足要求，但是本文所设计的制导律明显对目标机动的鲁棒性更强。两种制导律基本上都能在制导末端使得落地角收敛到约束值附近，弹道也能够接近垂直击顶。从加速度指令曲线上看，制导律A的指令输出曲线平滑，略好于制导律B。

此外，也对固定目标和运动目标进行了仿真，本文所设计制导律的脱靶量和期望落角均都能很好的满足要求。

4 结束语

导弹以期望落角命中目标，制导律中则必须有2个控制量，一个控制落角误差，一个控制脱靶量。然而，2个控制量之间又存在矛盾，所以要协调好2个量之间的关系。常用的方法是最优控制理论，通过在性能指标中加入落角约束条件和视线稳定条件，然后求解逆里卡提(Riccati)微分方程得到最优控制律。本文使用反步控制法和李亚普诺夫原理，对落角误差和脱靶量分成两步控制，求解出了新型带落角约束的三维制导律，满足了大落角约束制导律的设计要求，并且在对攻击机动目标的方面要略优于落角约束最优制导律，同时结构简单，易于工程实现。

[1] 刘永善，贾庆忠，刘藻珍.电视制导侵彻炸弹落角约束变结构制导律[J].弹道学报，2006，18(2)：9-14.

LIU Yong-shan，JIA Qing-zhong，LIU Zao-zhen.Variable-Structure Guiadance Law with Terminal Angular Constr aint of Video-Guided Penetrating Bomb[J].Journal of Ballist ics，2006，18(2)：9-14.

[2] SHNEYDOR N A.Missile Guidance and Pursuit[M].Sawston:Woodhead,UK,1998.

[3] Chang-Kyung Ryoo，Hangju Cho，Min-Jea Tahk.Optimal Guidance Laws with Terminal Impact Angle Constraint[J].Journal of Guidance Control & Dynamics,2005，28(4)：724-732.

[4] 贾庆忠，刘永善，刘藻珍.电视制导侵彻炸弹落角约束变结构反演制导律设计[J].宇航学报，2008，29(1)：208-214.

JIA Qing-zhong，LIU Yong-shan，LIU Zao-zhen.Variable-Structure Backstepping Guidance Law with Terminal Angular Constraint for Video-Guided Penetrating Bomb[J].Journal of Astronautics，2008，29(1)：208-214.

[5] Gyorgy Hexner，Tal Shima.Stochastic Optimal Control Guidance Law with Bounded Acceleration[J].IEEE Transactions on Aerospace & Electronic Systems，2007，43(1)：71-78.

[6] ZARCHAN P.Tactical and Strategic Missile Guidance[M].Virginia:AIAA，Reston,2012.

[7] Katsuhiko Ogata.Modern Control Engineering[M].Englewood Cliffs: Prentice-Hall,1970.

[8] BRYSON A E，HO Y C.Applied Optimal Control[M].Waltham:Blaisdell，1969.

[9] Gregory F Bock.Augmented Proportional Navigation Guidance Law Using Angular Acceleration MeasuremeNts[P].United State Patent,2008.

[10] Rafael T Yanushevsky.Methods and Systems for Guiding an Object to a Target Using an Improved Guidance Law[P].United State Patent,2007.

[11] Ronen Atir，Gyorgy Hexner，Haim Weiss.Target Maneuver Adaptive Guidance Law For A Bounded Acceleration Missile[J].Journal of Guidance,Control,and Dynamics,2010,33(3):695-704.

[12] Vitaly Shaferman，Tal Shima.Linear Quadratic Differential Games Guidance Law for Imposing a Terminal Intercept Angle[C]∥Guidance,Navigation,and Control,2008 AIAA Conference and Exhibit,Honolulu,2008.

[13] 孙胜，周荻.考虑导弹自动驾驶仪动特性的三维非线性导引律[J].宇航学报，2009，30(3)：1052-1056.

SUN Sheng, ZHOU Di.Three-Dimensional Nonlinear Guidance Law with Consideration of Autopilot Dynamics[J].Journal of Astronautics，2009，30(3)：1052-1056.

[14] 周荻，曲萍萍.考虑导弹自动驾驶仪二阶动态特性的有限时间收敛导引律[J].航空兵器，2013,30(3)：9-12.

ZHOU Di, QU Ping-ping.Finite Time Convergence Guidance Law Accounting for Second-Order Dynamics of Missile Autopilots[J].Aero Weaponry，2013,30(3)：9-12.

[15] KIM K S，JUNG B，KIM Y.Practical Guidance Law Controlling Impact Angle[J].Proceedings of the Institution of Mechanical Engineers Part G：Journal of Aerospace Engineering，2007，221(1)：29-36.