轴向引伸仪初始应变归零对应变疲劳试验的影响研究

摘 要：基于试验原理的分析及公司间相同试验的数据差异性研究比对，本文采用了轴向低循环疲劳试验（LCF）初始应变的不同归零方式，对常用非延性金属材料，设定实验模型，对试验结果进行数理比较分析，得到试验正式开始前的初始应变值保持在±0.0005mm/mm范圍内，弹性模量或应力幅的误差均小于1%。

关键词：低循环疲劳LCF；初始应变ε0；弹性模量E

DOI：10.16640/j.cnki.37-1222/t.2017.24.242

0 引言

随着科技的不断发展，发动机的涡轮等转动部件工作在高温、大应力和有限寿命情况下，进而大量地使用高性能合金材料。研究这些材料的常、高温低循环疲劳[5]（LCF）性能，对工程部件的疲劳设计制造、改进、质量及可靠性等具有重要意义和价值。

实际工作中，试验人员按照已有的试验标准进行，对试验标准中未进行规定的试验技术细节，常按期积累的工作经验来进行，这样导致试验误差的产生和试验结果的不一致。本文暂不考虑其它影响因素，仅从初始应变归零的问题进行讨论。轴向LCF试验中，因安装应变仪会随机产生初始应变或试样加温保温完成后因温度的变化产生初始应变，这种初始应变值每次试验中并不相同，必须在初始载荷为零（或规定）的情况下进行归零。这种在疲劳试验正式开始前（零点）初始应变的归零对试验参数产生多少影响？目前国内外对这问题的研究极少。GB/T15248《金属材料轴向等幅低循环疲劳试验方法》[1]对影响试验参数的初始应变的归零未作规定，本文主要通过理论分析、验证对比试验和实际试验结果比对来探讨这种影响，这对试验人员进一步掌握低周应变疲劳试验技术，提高试验结果准确性、有效性，为修订试验方法、标准提供科学试验数据。

1 试验部分

1.1 试验前理论分析

应变仪依照不同型号具有其固定的标距L0，如25mm或12mm等，在机器的应变计算模块中使用L0作为控制和计算。当应变仪安装在试样上时，会产生随机的初始应变ε0，进行试验之前须将初始应变归零，才能正式进行试验（否则此初始应变会递加到试验应变上，即使微小的初始应变也应该清零），此时应变仪在试样上应变零位的标距为L0+L0*ε0；而在高温试验中，情况也类似，当试样从室温[2]升到试验温度并稳定时，试样的膨胀会增加温度应变，若总应变为εT，此时应变归零后，引伸仪在试样上零位的标距为L0+L0*εT；由以上两种情况可以设定在任何应变不为零（总的初始应变为εt0）时，归零后在零点真实的应变仪规长Lc=L0+L0*εt0。假如试验的应变值为εD，实际上的真实应变值为εT=（L0*εD） /（L0+L0*εt0）

可得 εT=εD /（1+εt0） （1）

由（1）可知，当初始应变εt0<0时，εT>εD；

当初始应变εt0>0时，εT<εD；

也就是说，在初始应变不为零的情况下，应变归零后，在试验过程中所产生的真实应变εT值与当初始的应变为零时试验所测控的应变εD值在原理上是有差别的。这种差别在一定控制范围内会很小，有时可能产生足够明显的差别，这会影响到试验用于计算的弹性模量、应力乃至疲劳寿命Nf等。

低循环疲劳（应变）试验中，循环应力幅变应幅满足：

△σ/2=K′ （△εp/2）n′ （2）

其中n′循环应变硬化指数，k′循环强度系数。

低循环疲劳（应变）试验中弹性应力幅与寿命或弹性应变幅与寿命的关系为：

△σ/2=σf′（2Nf）b 或△εe/2=（σf′/E）（2Nf）b

塑性应变幅与寿命的关系为：△εp/2=εf′ （2Nf）c

总的应变幅△εt/2=△εe/2+εp/2

即 △εt/2=（σf′/E）（2Nf）b+εf′ （2Nf）c （3）

其中σf′弹疲劳强度系数，b疲劳强度指数，εf′疲劳延性系数，c疲劳延性指数。

非弹性疲劳试验对同一试样不具有可逆性，即在过弹性阶段有限循环周次的应变疲劳试验无法控制试样本身的性质的变化，不利于数据结果的科学对比。而在弹性范围内，可以方便地用同一试样在完全同样的试验条件下进行不同初始应变的对比试验。

试验在弹性范围内满足胡克定律，则（3）式可见转化为：

试验的应力幅值 △σ=Ef*△εe （4）

同理，试验的（计算）动态弹性模量 EfC=△σ/△εD。

例如A、B、C三个试验分别以εA>0、εB≈0、εC<0的初始应变归零，在试样的弹性范围内进行试验条件完全相同的应变疲劳试验。按照应变仪的测控原理，计算弹性模量时，在试验技术参数相同的情况下，A、B、C都具有相同的试验应变幅值△εe，按照1.1中（1）式，三者产生的真实应变应该有差别，即εAT<εBT<εCT，而试验材料本身的弹性模量Ee在相同试验环境条件下不变，按照胡克定律，故A、B、C试验中所得的真实应力应该满足

σAT=E*εAT<σBT=E*εBT<σCT=E*εCT，

因用于计算弹性模量的实际应力不同，所以试验应该测量到三种不同的弹性摸量值，即

EAT=σAT/εE

那么，只要在同一试样在完全同样的试验条件下进行二个不同极性初始应变的试验，通过对比其弹性模量或应力幅值结果，就可验证上述分析。

1.2 试验设备和环境条件、试样

MTS370 （LANDMARK），应用软件MPE，试验室温度：23℃，湿度：70%，试样：螺纹连接等截面圆棒试样；所有应变仪都在室温下进行线性标定；试验机的同轴度：计量所校检满足国标要求。

1.3 验证试验方案

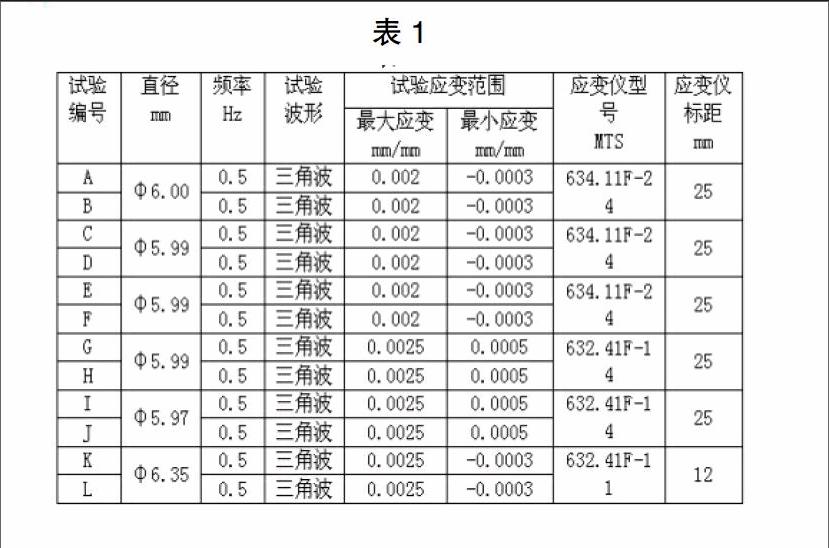
按照1.1所作的分析，设定验证试验方案如表1。

注：表中A和B作为一对试验，以进行相互对比，同理，C和D、E和F、G和H、I和J、K和L各为一对。

1.4 验证试验初始条件

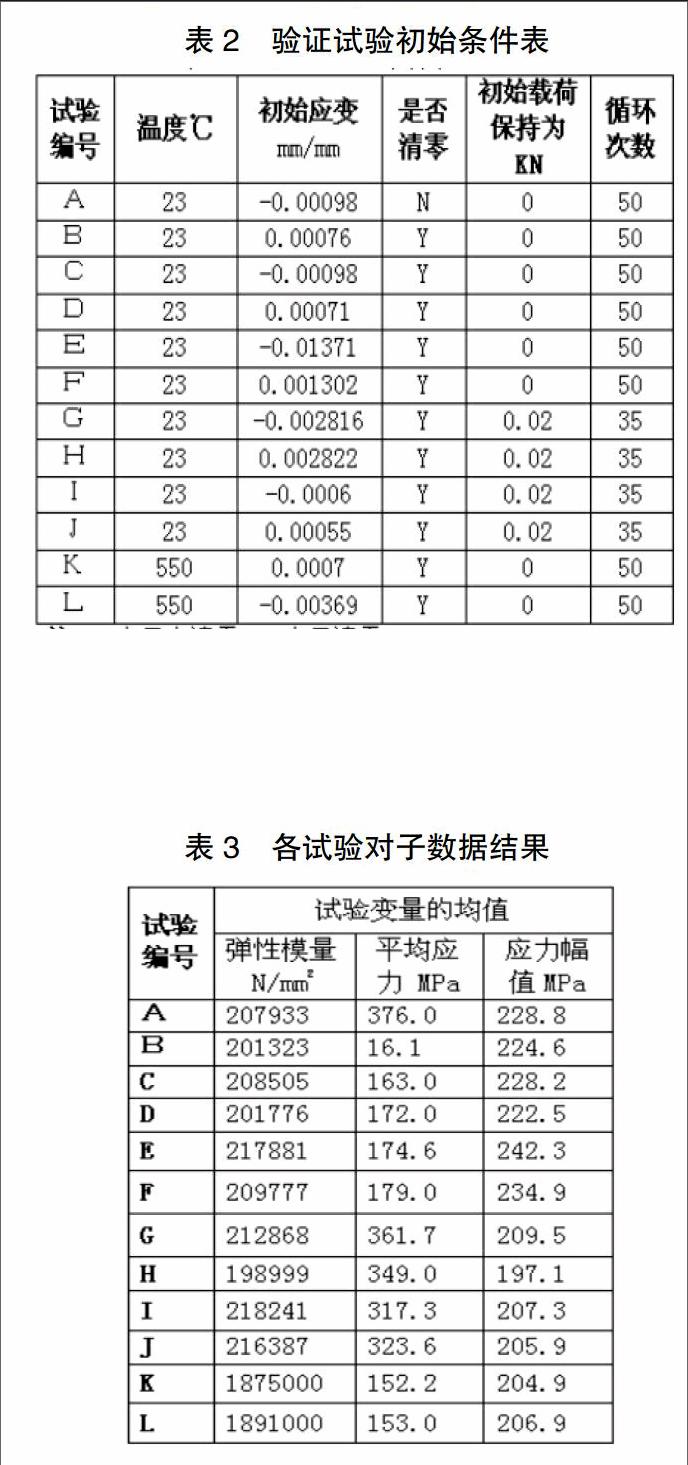
试验过程：应变仪室温下按其标距标定归零，按照GB/T12548试验标准安装好试样，装好应变仪，初始应变清零/或不清零，此过程中，初始载荷一直保持恒定（0或0.02KN），开始执行试验，达到给定的循环周次时停止，各验证试验初始条件如表2。

注：N表示未清零，Y表示清零。

2 结果与讨论

2.1 各验证试验对子数据结果

2.2 A组与B组对比分析

由A，B对比可知当初始应变未清零时，由于应变的叠加，A、B个试验的峰值应力及平均应力都向相反方向发生很大的偏移，试验完全改变，说明在试验中必须将初始应变清零。

2.3 C组与D组对比分析

C试验的弹性模量均值EC=208505 N/mm^2 及应力幅均值σC=228.2MPa均大于D试验的弹性模量均值EC=201776 N/mm^2及应力幅均值σC=222.5MPa，相对误差分别为

δECD=3.28%，=δσCD=2.53%。

2.4 E组与F组对比分析

E试验的弹性模量均值EE=217881 N/mm^2 及应力幅均值σE=242.3MPa均大于F试验的弹性模量均值EF=209777 N/mm^2及应力幅均值σF=234.9MPa，相对误差分别为δEEF=3.79%，δσEF=3.01%。

2.5 G组与H组对比分析

G试验的弹性模量均值EG=213013 N/mm^2及应力幅均值σG=209.5MPa均大于H试验的弹性模量均值EH=198993 N/mm^2及应力幅均值σH=197.02MPa，相对误差分别为δEGH==6.806%，δσGH =6.14%，两者误差很大。

2.6 I组与J组对比分析

I试验的弹性模量均值EI=218421 N/mm^2及应力幅均值σI=207MPa均大于J试验的弹性模量均值EJ=216458 N/mm^2及应力幅均值σH=205.5MPa，相对误差分别为δEIJ=0.903%，δσIJ=0.727%，两者误差较小，小于1%。

2.7 K组与L组对比分析

K试验的弹性模量均值EK=186014 N/mm^2及应力幅均值σK=203.6MPa均大于L试验的弹性模量均值EL=189138N/mm^2及应力幅均值σL=208.9MPa，相对误差分别为δEKL=-1.665%，δσL=-2.57%。

2.8 验证试验数据分析、讨论

实际上，应变控制疲劳试验中存在初始应变不可避免，初始应变的归零对试验的影响也确定存在，应该把这些影响限定在足够小的范围内。即在试验开始前，将初始应变值控制在一个规定范围，从而使其产生的试验误差在可接受的程度。

按2.1节中，A、C两个试验的初始应变分别为εA、εC，按①式甲，乙两个试验的真实应变差为

dεTAC=εTA-εTC

=（1/（1+εA）-1/（1+εC））*εD

应变相对误差δAC=dεTAC/εD

=1/（1+εA）-1/（1+εC）

=（εC-εA）/（（1+εA）*（1+εC））

一般应变仪的量程范围在±5%以上，εA，εC也不会超过5%，则（1+εA）*（1+εC）≥（（1+5%）*（1-5%））=1.05*0.95。

=0.9975≈1即A，C两个试验的应变相对误差 δAC≈（εC-εA） （5）

一般动态应变仪本身的测量精度为±0.5%（1%），我们使用的应变仪量程范围為±10%， 那么最大量程的相对误差±（0.5%*10%）=±0.05%，我们可以规定初始应变相对误差-0.05%≤δ≤0.05%，按照式（5）

即：-0.05%≤（εt0乙-εt0甲）≤0.05%，

把理想的试验初始点定义为初始的应力及应变初始值皆为0（无初始应变），那么此点也可以作为规范初始应变相对误差时初始应变的中点，则试验开始前归零的初始应变应该控制在：-0.05%（-0.0005mm/mm）≤εt0≤0.05%（0.0005mm/mm），而这在试验中是能够做到的。从I和J试验之间的对比，可以看到在此范围内的初始应变归零对试验结果的偏差并不大，弹性模量及应力范围两者的误差都小于1%。

3 结论

（1）本文通过试验原理的分析结合具体对比试验数据，论证分析得出在轴向低循环疲劳试验（LCF）中初始应变的归零对试验本身可能产生大的影响，如本文对比试验中弹性模量、应力幅等试验参数产生最大达7%的相对误差；

（2）通过理论计算及试验验证，提出处理方案，即将试验正式开始前的初始应变值保持在±0.0005mm/mm范围内；弹性模量及应力范围两者的误差都小于1%，从而在试验中得到更准确的数据结果。

参考文献：

[1]钟斌，张国栋，何玉怀等.GB/T15248-2008金属材料轴向等幅低循环疲劳试验方法[J].2008.

[2]北京航材院，HB/Z112-1986材料疲劳试验统计分析方法[S].1986.

[3]ASTM委员会.E606-04低周疲劳试验标准规程[S].2004.

作者简介：盛廷国（1981-），男，本科，工程师，研究方向：金属力学性能分析。endprint