按图索“迹”，攻克解题难点

付培军

带电粒子在复合场中的运动问题，能很好地考查考生空间想象能力、综合分析能力和运用数学知识解决物理问题的能力，常以压轴题的形式出现。试题一般结合运动、力、能量等知识点，覆盖面广，综合性强，是高考中拉开得分档次的关键。

一、运动情形

复合场是指电场、磁场、重力场中的三者或其中任意两者共存，在复合场中运动的电荷有时可不计重力，如电子、质子、α粒子等微观粒子；也有重力不能忽略的宏观带电体，如小球、液滴、微粒等。带电粒子在复合场中的运动情况虽然较为复杂，但同样遵循力和运动的基本规律。

（1）静止或匀速直线运动。若处于静止状态则不受洛伦兹力作用，肯定是重力和电场力平衡；若在电场力、重力和洛伦兹力共同作用下做直线运动，因电场力和重力为恒力，洛伦兹力随速度改变而改变；若速度大小变化，垂直速度方向上的合力就要变化，电荷就会脱离原来的直线轨道而沿曲线运动，因此电荷的速度一定不变。

（2）电荷在复合场中做匀速圆周运动。由于匀速圆周运动的条件是所受合外力大小恒定、方向时刻和速度方向垂直，只有洛伦兹力可满足该条件，因此电荷在复合场中做匀速圆周运动时，除洛伦兹力以外的所有力的合力必为零。一般情况下因粒子的速度大小和方向均不断变化，粒子只能做非匀变速曲线运动。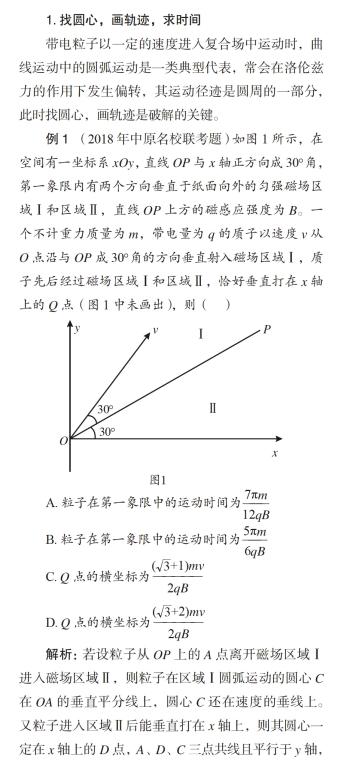

二、难点突破

带电粒子在复合场中的运动情形多种多样，涉及的知识点多，综合性强，难度大，但求解此类问题还是有一定的方法和思路可循的，考生可以抓住以下几个问题进行突破。

1. 找圆心，画轨迹，求时间

带电粒子以一定的速度进入复合场中运动时，曲线运动中的圆弧运动是一类典型代表，常会在洛伦兹力的作用下发生偏转，其运动径迹是圆周的一部分，此时找圆心，画轨迹是破解的关键。

例1 （2018年中原名校联考题） 如图1所示，在空间有一坐标系xOy，直线OP与x轴正方向成30°角，第一象限内有两个方向垂直于纸面向外的匀强磁场区域Ⅰ和区域Ⅱ，直线OP上方的磁感应强度为B。一个不计重力质量为m，带电量为q的质子以速度v从O点沿与OP成30°角的方向垂直射入磁场区域Ⅰ，质子先后经过磁場区域Ⅰ和区域Ⅱ，恰好垂直打在x轴上的Q点（图1中未画出），则（ ）

A.粒子在第一象限中的运动时间为

B.粒子在第一象限中的运动时间为

C. Q点的横坐标为

D. Q点的横坐标为

解析：若设粒子从OP上的A点离开磁场区域Ⅰ进入磁场区域Ⅱ，则粒子在区域Ⅰ圆弧运动的圆心C在OA的垂直平分线上，圆心C还在速度的垂线上。又粒子进入区域Ⅱ后能垂直打在x轴上，则其圆心一定在x轴上的D点，A、D、C三点共线且平行于y轴，结合题意可绘出粒子运动的径迹如图2所示。

点评：解有关带电粒子的多解或周期性问题时，要弄清楚复合场的组成特点及场的变化情况，确定多解或周期性形成的原因，正确分析带电粒子的受力情况，画出粒子的运动轨迹，并且至少要画出一个周期的运动轨迹示意图，注意相邻过程的衔接点，再应用相关规律求解。当带电粒子做复杂的曲线运动或有约束的变速直线运动时，一般用动能定理或能量守恒定律求解。

3. 分析运动中的临界、极值或磁聚焦问题

带电粒子在复合场中的运动过程中往往存在临界和极值问题，有时还夹杂着磁聚焦问题，难度大。求解时要对题目中所涉及的物理情景理解清楚，对物理过程有正确的认识。

例3 （2017年中原名校联考题）如图6所示，圆柱形区域是垂直纸面向里的匀强磁场B的横截面，一质量为m电量为+q的粒子从M点沿与直径MN成45°角的方向以速度v射入场区。若粒子射出磁场时与射入磁场时运动方向间的夹角为135°，P点是圆周上某点，不计粒子重力，则（ ）

A.粒子做圆周运动的轨道半径为

B.磁场区域的半径为

C.粒子在磁场中的运动时间为

D.若粒子以同样的速度从P点射入，则从磁场射出的位置必定与M点入射时从磁场射出的位置相同

解析：如图7所示，由速度转向角为135°，知粒子从C点竖直向上射出，圆心为D点，由几何关系知四边形MOCD为菱形，即粒子圆运动的轨道半径和磁

场区域的半径相同，由qvB=知R=，即选项B对A错；由速度转向角为135°知t=T，又T=知t=，即选项C错；若粒子以同样的速度从P点射

入，则轨道半径不变，圆心在图7中的E点，四边形POCE也为菱形，粒子经PC弧过C点，此时与P点的位置无关，由磁聚焦知都会过C点，故选项D对。

点评：本题中粒子从不同位置射入而从同一位置射出，属磁聚焦问题。一般地，在复合场中运动时，要根据受力情况推断粒子的运动情况，再建立关联方程求解。处理临界或极值问题时，一般先分析两种物理现象及其与临界值相关的条件，再用假设法、极限法或数学方法求出临界值，依所给条件与临界值间的关系求解。而有关磁聚焦的问题，一般要结合粒子速度的变化情况，分析出粒子的运动特点，在动态中确定粒子圆周运动的圆心，绘制粒子运动的草图，把握好边界粒子运动的轨迹，再用几何关系求解。

Tips：解题方法归纳

求解带电粒子在复合场中的运动问题时，首先要弄清是怎样一个复合场，然后才能对带电粒子的受力及运动情况进行分析。求解步骤为：①划分过程，即将粒子运动的过程划分为几个不同的阶段，对不同的阶段选取不同的规律处理；②画运动轨迹，即根据受力分析和运动分析，大致画出粒子的运动轨迹，有利于形象、直观地解决问题。③找关键点，即确定带电粒子在场区边界的速度（包括大小和方向）是解决该类问题的关键。endprint