理清困难 寻找突破
2017-12-29刘妍霞



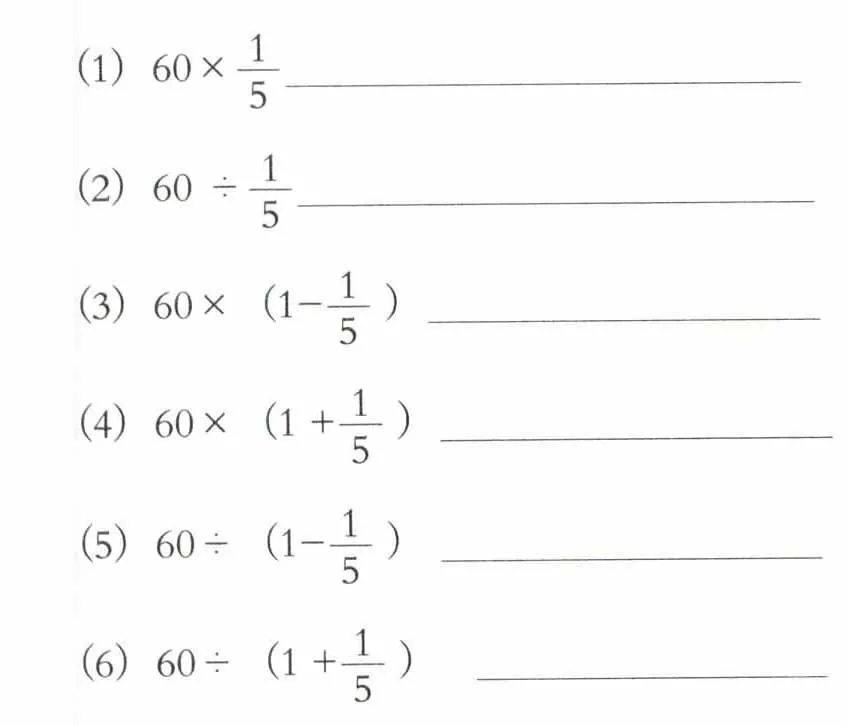
“数学是思维的体操”,它能开发学生的智力,培养学生的思维能力,有助于学会思考、学会学习、学会创造。
知识是思维的载体,学习数学的目的是为了促进智慧的生长。郑毓信教授曾强调:分数是数学思维真正进入小学数学的地方。分数也是一些学生在数学学习中表现出真正困难的实际起点。
一、为什么困难
分数是学生数的概念的第一次扩展。在认识分数之前,学生认识的数都是万以内的整数,比如:0、1、2、3、4……
数的产生来源于实际生活的需要。朱国荣老师认为,在分数意义拓展时,分数被用来表示一个量与另一个量的比的关系。比如,把一堆苹果平均分成两份,其中的一份是苹果总数的。苹果总数的可能是1个,也可能是2个、3个……,当苹果总数是1个时,苹果总数的就是个。这个不再具体表示数量的多少,而表示部分和整体数量之间的关系。和学生认识自然数的经验和过程不相一致,不符合学生认识数的逻辑顺序。这也是学生在认识分数时普遍感到模糊、困难的根源。
二、困难在哪里
经过一段时间的分数教学,感触颇深。苏教版《义务教育教科书·数学》“分数”这部分知识分四次教学,安排如下:
三年级上册第七单元“分数的初步认识(一)”,认识一个物体(或图形)的几分之一(几分之几),同分母分数的大小比较,同分母分数的加、减法。
三年级下册第七单元“分数的初步认识(二)”,进一步丰富对分数的理解,把几个物体组成整体,认识整体的几分之一(几),求整体的几分之一(几)是多少。
五年级下册第四单元“分数的意义和性质”,教学分数的意义和分数单位,分数与除法的关系,求一个数是另一个数的几分之几,真分数与假分数,把假分数化成整数或带分数,分数与小数的互化,分数的基本性质,约分通分。
六年级上册第二单元“分数乘法”,分数与整数相乘,求一个数的几分之几是多少的实际问题,分数乘分数,分数连乘及其实际问题,认识倒数。
六年级上册第三单元“分数除法”,分数除以整数,整数除以分数,分数除以分数,简单的分数除法实际问题,分数连除和乘除混合运算。
六年级上册第五单元“分数四则混合运算”,分数四则混合运算,稍复杂的分数实际问题。
经过梳理教材,有两个知识点在学生的思维的提升方面起着至关重要的作用,可谓是两次飞跃。
(一)第一次飞跃——分数的意义
学生对分数认识,首次感受到一个数不再单纯的表示量,它是从感性走向理性的开始。分数的意义,在分数这部分知识中起引领作用,不论是分数的基本性质,分数大小的比较,约分、通分及四则计算,分数实际问题都建立在分数意义之上。从数学的角度来看,分数的引入是为了解决在整数集合里除法不是总能实施的矛盾。因此, 让学生认识到将一个物体、一个图形、一个计量单位、一些物体作为整体平均分,抽象出单位“1”,在教学中引导学生理解和掌握分数的概念,分数中的其它知识也会迎刃而解。
(二)第二次飞跃——分数乘法
分数乘法的计算方法的推导和有关分数乘法的实际问题的解决,为学生对分数作为分率的理解提供了机会。从中可以认识到分数不仅可以表示一个具体的量,还可以表示部分与整体之间的关系。学生从具体的数的世界转入到抽象的数的世界,认知上的一次跳跃,又是一次理性的提升。
三、如何突破困难
(一)让数学思维在“说”中渐入佳境
数学语言是数学思维的工具,是数学思维的外壳。爱因斯坦曾说过:“一个人智力的发展和形成概念的方法,在很大程度上取决于语言。”小学生语言区域狭窄,更缺乏数学语言。实践证明:语言能力提高了,思维能力也得到很好的发展。因此,在分数教学中,发展学生的思维,就要加强说理训练。
1.引导模仿,仿照着说
模仿是提供一种数学语言表达的范式,让学生仿照着范式思考,从而培养学生思维的准确性。在进行分数实际问题教学中,解题的关键是找准题中的关键句、单位“1”和数量关系,而题中的关键句的呈现形式各不相同。如:“十月份用水量比九月份节约”“其中是第一天用的”“ 一袋米吃了”等等。在理解这些句子中分数意义时,可以让学生试着这样说:把哪个量看作单位“1”?谁的几分之几是多少?数量关系式是什么?通过多次训练,学生不仅掌握了分析数量关系的方法,而且从儿童的自然语言,逐步过渡到规范、准确的数学语言,提高了学生数学语言表达能力,也促进了学生思维能力的提高。
2.引导联想,变着法说
引导学生联想,通过一个条件(关系)推出与其相关的条件(关系),培养学生的发散思维。在解决分数实际问题系时,关键句不仅可以表述成分数的形式,还可以表述成其他形式。如:根据“盐是盐水的”,启发学生联想:水是盐水的,盐是水的,盐比水少,盐与盐水的比是( ):( ),鹽与水的比是( ):( ),水是盐的( )倍等等。
在教学中,教师创造数学语言训练的机会,循循善诱,让学生在“说”中“思”,在“思”中“说”,培养学生表达自己见解的习惯,鼓励学生敢“想”,敢“说”,敢“与众不同”,对提高学生的求异思维起到事半功倍的效果。
3.引导反思,有条理地说
由于学生自我意识的发展还不成熟,对自己的思维破绽、错误不易注意。当学生对所学的内容有了较全面的理解和掌握时,教师应及时引导学生反思,让学生说解题思路、解题步骤。在说的过程中,不断调整自己的思维,试着自我总结,自我评价,提炼思想方法并形成解题策略。因此,在解决分数实际问题的过程中,应着力培养学生“自我反省”的习惯,有条理的表述思维过程。
4.引导比较,自由地说
在分数教学中,有很多具体内容不同,但有着相似结构的实际问题,教师可以创造机会,让学生仔细观察,鼓励学生独立思考,比较其相同点和不同点,自由的发表自己的见解,从联系中探索内在规律,这样,不同于单纯的就题讲题,还可以形成“自由辩论”的学风。
如:梨有60千克, 。苹果有多少千克?
(6)60÷(1 + )
通过各抒己见,探索结构之间的关系,把相同的思考过程提炼出来,进一步抽象化、符号化。这样,在面对新的实际问题时,就能把已有的方法和策略,类推到新的情境中,迅速找到解决问题的方法。通过这样的练习,可以丰富学生的联想,增强思维活力,提高思维敏捷性。
(二)让数学思维在“图”中越飞越高
运用线段图解决问题是一种数学技能。围绕“解决分数实际问题”对我校六年级学生做了调查问卷。情况如下:
我们总想学生把线段图当做一种解题的策略,信手拈来。从上面的数据可以看出,对于大多数学生来说,成人看似简单的线段图,学生理解有一定的困难。
1.在具体情境中理解分数的意义
如:明明家有鹅4只,是鸡只数的,有几只鸡?
“鹅是鸡只数的”中表示:1只鹅对应3只鸡,2只鹅对应6只鸡,以此类推,4只鹅对应12只鸡。
理解的意义是一个破题的过程,清楚的破题,就自然而然地得到了解题的思路。因此,在解决实际问题的教学过程中,应重视破题这个环节。
2.由“文”到“图”
从儿童视角出发,将数学知识的过程、方法和结果用图像进行表征,勾勒出数学知识的本质属性。借助于学生能见到的或想到的几何图形、线段图等,对数量关系的直接感知,帮助学生理清数量关系:哪个量作为单位“1”,哪部分是单位“1”的几分之几,抽象的数量关系变得直观,有利于学生把握数学问题的本质。
3.图式结合,强化训练
教材中提供现成的线段图,帮助学生理解题意,但学生并不理解画线段图的过程。教学中让学生自己试着画,还原图形,然后与教材中的图对照,发现错误及时纠正。学生会画线段图不是一朝一夕能解决的问题,教师还应多鼓励。
用线段图来表征数学问题,可以帮助学生轻松的解答复杂关系的实际问题,既培养了学生的能力,又促进了学生思维的发展。因此画线段这样的图式意识是一种重要数学观念,会用图式表征是关键数学能力,图式思维更是必备学习品质。
(作者单位:江苏省南京市溧水区实验小学 )
(责任编辑:杨强)
