含阶梯结构的高层楼梯井内烟气湍流及输运特征量的全局敏感性分析
2017-12-29徐君儒熊才溢
徐君儒,邱 榕*,熊才溢,蒋 勇,黄 玥
(1. 中国科学技术大学火灾科学国家重点实验室,合肥,230026; 2.重庆市渝北区公安消防支队,重庆,401120)
含阶梯结构的高层楼梯井内烟气湍流及输运特征量的全局敏感性分析
徐君儒1,邱 榕1*,熊才溢1,蒋 勇1,黄 玥2
(1. 中国科学技术大学火灾科学国家重点实验室,合肥,230026; 2.重庆市渝北区公安消防支队,重庆,401120)
高层建筑竖井火灾中影响因素众多,并且各因素对高层楼梯井火灾中重要现象、关键数值等的影响大小不一,使得此类火灾中的实验或理论研究成本较高。通过建立全局敏感性分析平台,定量考察了高层楼梯井结构所涉及因素的影响大小,并能够方便地筛选掉对所考察量影响较小的因素,以降低实验或计算成本。使用数值模拟方法,通过CFD软件对包含阶梯几何框架的高层楼梯井结构火灾进行了共计60次工况计算。并且根据计算结果,使用全局参数敏感性分析方法,得出建筑尺寸、热释放速率、环境参数对高层楼梯井内烟气湍流特性及输运特性的敏感性排序。结果表明,火源热释放速率对各输出参数的影响均占38%以上。
楼梯井;敏感性分析;高层建筑;烟气;中性面
0 引言
城市化发展使得有着更高土地利用率的高层建筑被更多地使用,而高层建筑中因其高度较大、人员集中、功能结构复杂等特点使得其有着较大的火灾安全隐患。另外,高层建筑中的楼梯井等竖井结构使得此类型建筑中的火灾有着火灾发展迅速、烟气扩散快、人员疏散难的特点[1]。因此,针对高层建筑中的竖井结构,国内外学者做过大量的研究。
加拿大国家研究院的Klote等[2, 3]对火灾烟气控制系统的计算机数值模拟、测试方法等进行了研究,并且在之后的数年间,对竖井内烟囱效应进行了研究并提出竖向通道结构内烟囱效应的产生原因是温度差带来的压力分布。Sun等[4]分析了在楼梯井结构中楼梯结构对流场的影响,并得出了流场涡旋和温度的关系。
参数敏感性分析方法通过线性变化、傅里叶展开等方法得到特定输入参数对于特定输出参数的定性或定量分析。对于局部参数敏感性分析方法在火灾领域中的运用,可追溯至Khoudja[5]考察若干输入参数对早期CFAST输出结果的影响时使用的数学方法。Peacock等[6]通过偏导数敏感性分析方法研究了导热热损失分数对烟气层高度的影响。Kong等[7]使用相关系数、回归系数等统计系数也对DETACT- T2模型进行了参数敏感性分析。而对于全局参数敏感性分析方法,Albrecht和Hosser[8]采用自适应响应面法得到FDS中热释放速率、CO及soot生成量对烟气密度等的影响。Suard等[9]使用基于部分因子设计的敏感性分析方法对腔室火灾模型中部分输入参数进行了敏感性分析。全局参数敏感性分析方法的研究运用至火灾领域中的研究相对较少,且未运用至高层建筑竖井结构相关的火灾研究中。
本文使用CFD软件进行高层楼梯井火灾算例的数值重构,设计了10组实验,共计60个工况。通过CFD计算,得到敏感性分析所需输入输出参数数据,再利用全局敏感性分析方法,给出高层楼梯井火灾烟气行为中部分关键因素的定量敏感性排序。另外,前人对竖井火灾的研究模型通常仅考虑类似电梯井的空洞竖直结构,对楼梯井中的阶梯结构通常保持省略且未做研究,但在火灾发生时,电梯通道等常处于关闭状态,含阶梯结构的楼梯井内烟气现象对人员逃生等有着更直接的影响,并且阶梯结构对竖井中的烟气对流等行为影响显著,因此本文考虑加入阶梯结构的楼梯井通道中的烟气湍流及输运情况。
1 理论模型
1.1 参数敏感性分析方法
参数敏感性分析可以通过计算输入参数变化时所考察输出结果参数的变化,变化的输入参数对计算结果的影响定量分析。敏感性分析包含了局部及全局两种类型[10]。全局敏感性分析可以分析所有参数对输出的影响,可以考察参数间的交互作用,较局部敏感性分析更为优越[11]。故本文采用全局敏感性分析法。
Morris筛选法在每次变动某一参数的取值同时保持其它参数不变,在此条件下计算各参数的基本影响程度[12]。此筛选法得出的基本影响程度可以作为衡量参数重要性的指标,不同输入参数间不同的基本影响程度可以通过比较其大小甚至数量级来衡量其对输出参数的影响大小,并使用线性以及非线性的水平值,将参数的局部影响消除,是一种全局敏感性分析方法。Morris筛选法的核心公式如下:
di(x)=[y(x1,x2,…,xi-1,xi
+Δ,xi+1,…,xk)-y(x)]/Δ
(1)
式中di表示第i个参数的敏感性,Δ表示输入参数变化量。
按照Morris敏感性分析要求设置输入参数,如式2所示进行输入参数的初始化:
(2)
式中m表示k+1,k表示输入参数个数。式(2)中各变量含义汇总如表1所示,表示了输入参数设置的过程。矩阵B中0、1的位置在此式中分别表示了还未变化的参数和变化后的参数的位置,经过式(2),矩阵B*中也仅有0、1,表示变换后的相应参数位置。

表1 式(2)中各变量含义
通过式(2)的变换,降低所选取的输入参数的值对结果的影响。式(2)还保证每组有(输入参数个数+1)个工况,其中每两个工况间随机变动一个参数。通过变换,使得这k+1个工况中每个输入参数都会变化且仅变化一次。
1.2 湍流模型
FDS的计算中使用大涡模拟作为湍流模型或采用直接数值模拟[13]。本文使用大涡模拟模型进行火灾数值实验的计算。



(3)
FDS6中大涡模拟默认选用Deardorff模型,定义湍流粘度为:

(4)

(5)
2 数值模拟准备及设置
2.1 敏感性分析平台
将参数敏感性分析运用至高层建筑火灾领域。首先在FDS软件中,针对不同的输入参数,设置不同参数下的工况。每个工况经过CFD计算,得到相应的温度场、速度场、粘度场、浓度场等信息。这些信息通过后处理后,可以得出各输出参数。将对应的输入参数及后处理后的输出参数共同加入敏感性分析模块后得出敏感性分析结果。流程如图1所示。
需要先针对单组进行敏感性的计算,单组流程也可参考图1。在这样的一轮循环结束后,还需循环进行多次此过程,得出多组的敏感性分析结果以降低随机性。每个组的输入参数设置不同。如图2所示,首先使用输入参数,以及使用后处理所需数据通过各个后处理函数所得到的输出参数,计算单组敏感性。重复此过程,多组的敏感性分析结果。通过各组的敏感性分析结果,最后得到最终的敏感性分析结果。通过此耦合Morris筛选法的平台实现对高层楼梯井火灾的敏感性分析。

图1 敏感性分析流程Fig.1 Progress of sensitivity analysis
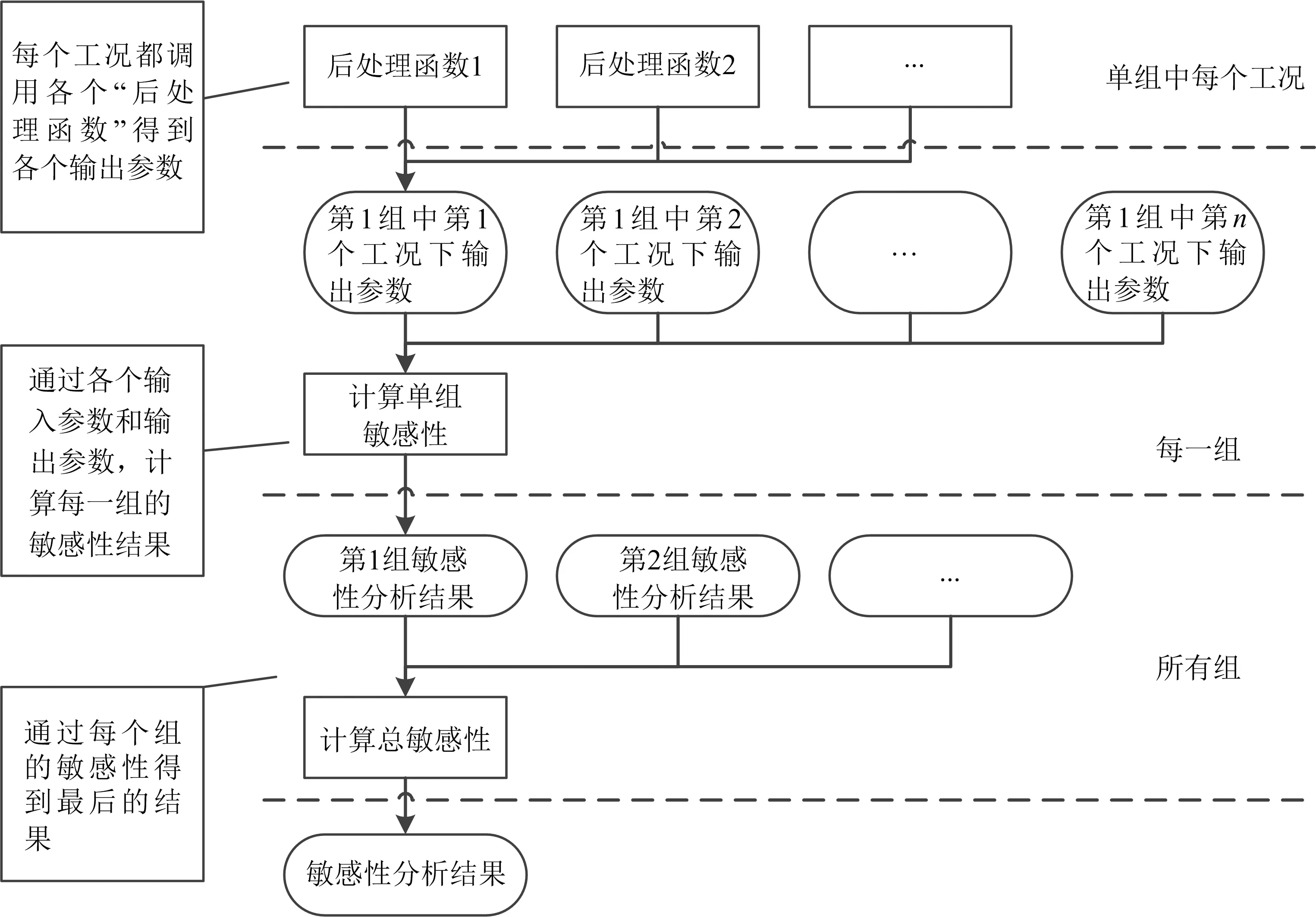
图2 敏感性分析平台框架Fig.2 Framework of the sensitivity analysis platform
2.2 计算设置
2.2.1 模型设置
本文根据实际某高层建筑楼梯井部分建模,得到长5.4 m、宽3.0 m、高36.55 m的楼梯井结构,楼梯井与楼层房间直接相连,中间无前室分隔。模型按照工程实际布局,包含各层及各半层平台以及楼梯道,如图3(a)所示。在火灾发生时,电梯通道常处于关闭设置,含阶梯结构的楼梯井对人员逃生等有着更直接的影响,因此本文在此对楼梯井的建模按照实际情况设置,考虑阶梯结构。设置火源发生于与楼梯井相连的房间内。此房间与楼梯井一层相连,房间尺寸按照建筑原型内与楼梯井相连房间参数设置,如图3(b)所示。

图3 模型结构Fig.3 Structure of the model
2.2.2 输入输出参数
考虑楼梯井中影响较大的因素。Harish和Venkatasubbaiah[14]研究了高层竖井横向纵向开口对内部气体流动的耦合作用,指出竖井与相连腔室的竖直连接口以及竖井内对外的竖直通风口对竖井内烟气流动模式影响巨大。Black[15]研究了众多因素对电梯井结构中火灾烟气运动的影响,得出电梯井宽度、室外风速、建筑材料属性等因素对此结构内烟气运动影响很小,而室外温度、井内通风口的影响相对较大,且不同季节的环境温度下结果差异可达50%。在许等[16]对竖井中性面位置的预测模型研究中,侧向开口的参数是预测模型中性面的重要参数。张[17]在其博士论文中得出火源功率与羽流上升时间的次方之间符合反比关系且影响温度峰值,并且火源规格对烟气温度、CO浓度的影响较为显著。因此,综合竖井结构火灾研究成果,考虑竖井内窗口尺寸、环境温度、火源房间与楼梯间房门尺寸、火源热释放速率5个因素作为本文研究的模型输入参数。
考虑楼梯井内烟气行为的重要指标作为输出参数。除上述竖井结构火灾研究[14- 17]中考虑的烟气上升速度、中性面高度、烟气温度、有害气体浓度这些火灾中关键问题外,Zhang等[18]在其对腔室火灾湍流特性的研究中考察了烟气湍流中温度场、速度场的脉动均值及脉动强度。因此,本文考虑井内中心线上某相同无量纲高度点的湍流温度均值、湍流温度脉动强度、纵向湍流速度均值、法向湍流速度均值以及建筑内中性面高度、烟气上升速度、烟气温度峰值、CO浓度峰值作为输出参数。
输入参数设置取值范围设定首先参考建筑实际尺寸及相关规程[19],并参考中国科学技术大学的许,张,李等[16, 20, 21]在对高层建筑竖井通道研究中的工况设置,考虑各输入参数取值范围。外窗宽度取值[0.8 m,1.2 m],环境温度取值[5 ℃,30 ℃],竖井及火源房间连通门宽度取值[0.8 m,1.2 m],火源热释放速率取值[3 MW,6 MW]。对输入输出参数无量纲化后再进行敏感性分析以降低模型间非独立关系。记竖井宽度为特征长度,特征长度与重力加速度之积的算术平方根为特征速度,特征长度除以重力加速度之商的算术平方根为特征时间。
3 结果与讨论
3.1 CFD结果后处理
因为FDS的计算结果给出的测点信息及场信息中并不能直接得出本文考量的所有输出参数,所以需要编写后处理函数以得到所需输出参数。按照前文所列输出参数,分别编写后处理函数。
3.1.1 湍流均值及脉动强度

图4 相同无量纲时刻下第一组前三个工况中心线上温度均值比较Fig.4 Mean temperature at centerline of the first three cases in group 1 at the same non- dimensional time moment
选取中心线上某无量纲高度相同的位置在相同无量纲时间范围内温度、速度分量均值。图4为某相同无量纲时间段内第一组前三个工况中心线上湍流均值比较,其中纵坐标均为无量纲高度。由图4可以看出单个参数变动对这些物理量存在影响。图4中所选取无量纲时间点为稳定前时间点,该时间点下烟气未在井内完全发展,仅显示至流场变化明显的位置。和无阶梯结构竖井中的湍流均值图形相比[18],加入阶梯结构中的湍流均值有较明显的随楼层的波动,此波动是由规律的阶梯结构造成的波动。
温度湍流脉动强度同Zhang等[18]使用的湍流强度公式,公式如下:

(6)
其中t′为湍流脉动。
湍流脉动计算选取相同无量纲时间段内湍流脉动。图5为第一组前三个工况在相同无量纲时间段内湍流温度脉动,单一参数变动对湍流脉动强度及均值均有较明显影响。

图5 第一组前三个工况在相同无量纲时间段内温度脉动Fig.5 Intensity of temperature fluctuation of the first three cases in group 1 at the same non- dimensional time period
3.1.2 中性面高度
中性面位置取烟气流动发展稳定时的烟气流动情况进行计算,本算例取烟气流动稳定时的流场数据进行计算。其中,各个工况所选取流动稳定的无量纲时间相同。按照中性面的定义,中性面为与外界压强相等的一层[22]。中性面高度计算首先选取各楼层窗户的中心点,考察此处的窗口法向速度,其中窗口朝外为正向。图6(a)为第一组第一个工况中各窗口法向速度随楼层高度的关系,其中的散点为窗口各楼层窗户的中心点,曲线为拟合曲线。如图6(a)所示,随着楼层增高,烟气有着由向楼梯井内部流动转为向楼梯井外部流动的趋势。在这里选取拟合曲线与直线V=0交点的纵坐标为中性面的高度。
图6(a)中各楼层窗口中心点速度分量拟合曲线中性面现象明显。图6(b)为未设置阶梯结构的竖井中的中性面计算情况。无楼梯阶梯结构的竖井模型中,中性面计算较高,符合Black[15]对于无阶梯结构竖井结构的研究数据,但是实际情况是包含阶梯结构的,中性面会因阶梯的存在对气体向上的对流造成阻碍。加入阶梯结构后,楼梯井内中性面位置较不加时偏低,本文加入阶梯结构以研究真实情况下楼梯井结构。

图6 各楼层窗口中心点速度分量散点及拟合曲线Fig.6 Horizontal velocity scatter at the center of windows and the fitting line
3.1.3 烟气上升速度
单点速度瞬时值或均值不能体现井内宏观烟气上升的快慢,本文考察宏观的烟气上升速度,即一定浓度烟气上升至一定高度的速度。烟气中烟颗粒带来的消光系数与火场中可见度有强相关性[23],本文引用视觉设备在火场中运行极限值[24]及性能化设计中小空间可见度的极限值5米为阈值,判定在火灾烟气发展稳定前相同无量纲时刻下,可见度低于阈值的最高点为烟气蔓延的最大高度,并以此定量分析烟气上升的快慢。通过遍历数据,标记在楼梯井结构内部的、能见度低于阈值的点,并忽略可见度高于阈值的点,且仅保留高度最高的点作为返回的输出参数。
3.1.4 物理量峰值
选取火灾烟气发展稳定前相同无量纲时间内所考察物理量湍流均值的峰值进行分析。选取该时刻下的最大CO浓度及最大温度。
3.2 数据整合后的敏感性分析结果
单组敏感性分析流程如图1所示,计算所有单组敏感性后,对各单组的敏感性结果进行数据统计,并通过敏感性分析平台中计算总敏感性函数得出最终结果。图7及图8为通过10组独立数据得出的湍流敏感性计算结果。各图的输入参数由上至下分别为窗口宽度、环境温度、竖井与火源房间连通口宽度、热释放速率。
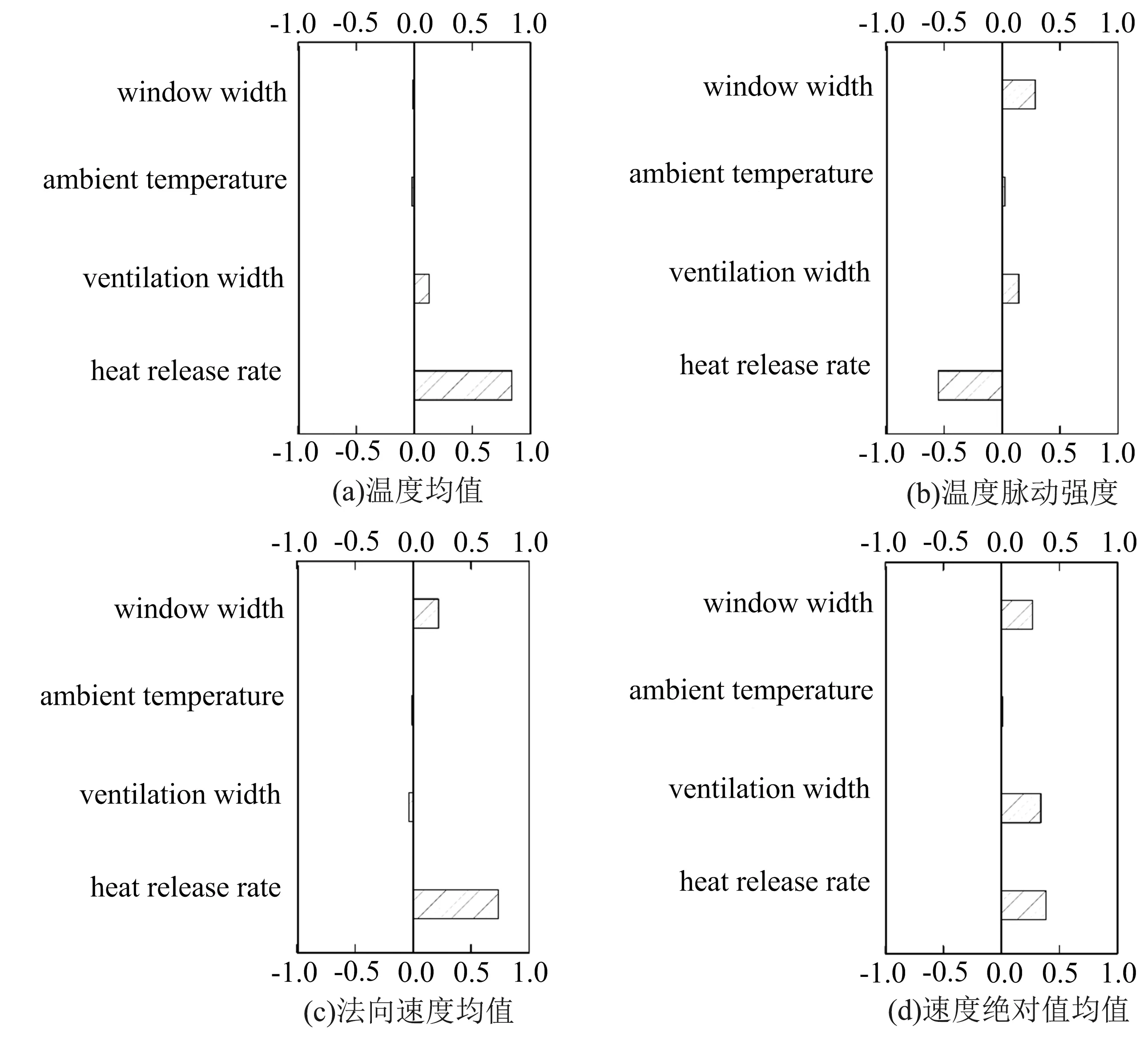
图7 影响楼梯井内湍流特性的各输入参数敏感性Fig.7 Sensitivity result of influence factors associated with turbulence characteristics
图7(a)中的敏感性数据显示了对于竖井内湍流温度均值影响最大的是火源热释放速率。外窗及连通口尺寸、环境温度三项远小于火源热释放速率对湍流温度均值的影响。火源热释放速率单项对温度均值的敏感性数值达到了+0.841,可以表示热释放速率对温度均值的数值为正向影响,即增大火源热释放速率将增大温度均值,且对湍流温度均值的定量影响在所有输入参数中的比值达到84.1%。火源房间与楼梯井的连通口尺寸的敏感性数值在所有因素中仅次于热释放速率,但数值仅有+0.130,明显小于热释放速率的影响。虽然环境温度、外窗尺寸对温度均值的影响非常直观,即环境温度给定了竖井内的起始温度且外窗尺寸和环境温度都影响着井内与外界对流换热,但是通过定量的敏感性分析,可得此二者对温度均值的影响与火源热释放速率相比而言可忽略不计。值得注意的是敏感性分析结果表明的影响大小是相对与本文各所选输入参数而言的,如输入参数中不考虑火源热释放速率,则连通口尺寸与其它参数相比将会对温度均值有较大影响。图7(b)中可反映上述四个输入参数对楼梯井内湍流温度脉动强度的影响程度。火源热释放速率在所有输入参数中仍然是影响最大的参数,敏感性数值达-0.547,其中负值表示此输入参数增大将抑制湍流脉动强度。外窗尺寸相比于对温度均值可忽略不计的敏感性,其对于温度脉动强度的敏感性较为显著,仅次于火源热释放速率,达+0.283。环境温度对脉动的影响较小。图7(c)为各输入参数对水平方向(外窗法向)速度分量均值的敏感性结果,火源热释放速率敏感性数值最高,达+0.733。不同于温度均值,对法向速度均值,外窗尺寸影响比火源房间与楼梯井连通口尺寸大。外窗尺寸敏感性数值为+0.217,远大于连通口敏感性的数值-0.036,因为井内烟气的水平运动和外窗有直接关联,让外窗尺寸影响更大。相比其他因素,环境温度影响仍然很小。图7(d)中展示了4个输入参数对速度绝对值均值的敏感性。其规律与速度分量均值类似,但火源房间与楼梯井连通口尺寸敏感性比重增大,由-0.036增至+0.339。连通口尺寸限制烟气发展阶段烟气进入楼梯井内的烟气流率,相比于气体在进入竖井后的水平运动,其对于烟气速度绝对值有更直接的影响。
由图7各子图中可知火源热释放速率对楼梯井内各湍流特性物理量影响在所有输入参数中均占较大比重,而环境温度作为输入参数之一,与热释放速率、外窗尺寸、火源房间与竖井连通口尺寸等参数相比影响很小。建筑内特定的结构,如外窗尺寸、火源房间与竖井连通口尺寸分别对湍流中某些物理量影响较大。
图8(a)反映出对楼梯井内中性面高度影响最大的输入参数是火源面积。由图8(a)可知,火源热释放速率对中性面高度的影响达到了+0.549,竖井和火源房间连通口尺寸对其影响达+0.343。虽然外窗尺寸的影响比起热释放速率很小,但仍然是环境温度影响的3倍。热释放速率、连通口及外窗尺寸的增大使得中性面位置上升。值得注意的是关于预测中性面的模型[16]表明连续的竖井内侧向开口宽度对中性面高度影响较大,但其研究未对其它参数进行耦合比较,且本例中为按照普通楼房采光及自然通风面积设置侧向开口,并非连续侧向开口。此敏感性分析结果表明正常尺寸的外窗宽度相较于火源热释放速率及竖井和火源房间连通口对中性面高度影响较小。另外,本算例中在楼梯井内设置了阶梯结构,对烟气的对流及中性面的形成有直接影响,因此此敏感性分析结果适用于包含阶梯结构的楼梯井结构,可能和未设置阶梯结构的竖井结构实验结果有所不同。烟气上升速度的影响因素比较可见于图8(b)。图8(b)中显示了火源热释放速率对于烟气上升速度影响较大,达+0.712。其余3个输入参数对烟气上升速度影响均远小于火源面积,这3者中影响最大的属外窗尺寸,达-0.160。火源热释放速率增大、火源房间与竖井连通口尺寸加大将对井内烟气上升产生的促进作用和外窗尺寸加大的排烟作用非常直观,敏感性实验结果在此基础上表明火源热释放速率增大的促进作用明显大于外窗尺寸加大的抑制作用,说明若要通过加大外窗尺寸来抵消火源热释放速率增大而带来的烟气上升速度的加快,在此量纲下加大的尺寸数值需要明显大于热释放速率增大数值。由图8(c)可得火源房间与楼梯井之间连通口和火源热释放速率对楼梯井内最大CO浓度影响较大。这4个输入参数中,仅外窗尺寸会对CO峰值造成较为明显的抑制,其余的参数如房门尺寸都对其有促进作用。楼梯井与火源房间之间的连通口是火源房间与楼梯井内CO物质交换的直接通道,火源热释放速率决定了CO的生成速率,通过外窗井内CO排至外界,三者影响均较大,但敏感性分析结果表明连通口及热释放速率对CO峰值的促进作用均大于外窗的抑制作用。环境温度仍然影响很小,仅有火源热释放速率影响的1/20以下,在热释放速率等因素加入考量时可忽略不计。图8(d)中展示了影响温度峰值的各输入参数的敏感性。火源热释放速率对于最高温度影响非常大,达+0.795,其余3个参数影响之和仅为热释放速率影响的1/4。外窗尺寸和环境温度对温度峰值的影响较小。计算结果显示各输入参数所对应的敏感性都是正值,表示各输入参数对最大温度的影响都是正向的,即这些输入参数在数值上的增大将使得最大温度增加。

图8 影响楼梯井内烟气特性的各输入参数敏感性Fig.8 Sensitivity result of influence factors of transport characteristics
通过敏感性分析结果中的敏感性数值,可以通过控制可控变量,对所关注的难以控制的现象进行一定程度上的调控,并且在将特定输出参数作为主要考察对象的情况时,着重设置对此输出参数影响较大的因素,而对影响较小的因素不作过多考虑。
4 结论
本文通过全局敏感性分析方法,对高层建筑楼梯井结构中的温度速度场湍流均值、脉动强度以及竖井内烟气输运现象如中性面高度等输出参数进行了关于建筑特定结构设计尺寸、火源热释放速率等输入参数的敏感性排序,得出了各输入参数对于这些特征输出量影响大小的定量分析。主要结论如下:
(1)火源热释放速率对楼梯井内的湍流现象及输运特性影响最为明显。在各输出参数的敏感性结果中,火源热释放速率对输出参数的影响均占38%以上。
(2)火源房间与楼梯井之间的连通口尺寸对竖井内湍流特性及输运特性影响明显,除井内温度场的湍流脉动及法向速度分量外,影响仅次于火源热释放速率。
(3)环境温度对本文所选输出参数的影响相比于火源热释放速率、自然通风口尺寸、火源房间与竖井连通口尺寸很小,对各输出参数影响均低于热释放速率的1/20。
(4)自然通风情况下外窗尺寸对温度湍流脉动、流场及输运特性影响不能忽略,而对平均温度场的影响相比于其他输入参数较小。
[1] Chen JQ. High- rise building fire and its countermeasures[J]. Fire Science and Technology, 2007, 26(2): 109- 113.
[2] Klote JH, Fothergill JW. Design of smoke control systems for buildings[M]. Washington DC: US Department of Commerce, National Bureau of Standards, 1983.
[3] Klote JH. A general routine for analysis of stack effect[M]. Washington DC: US Department of Commerce, National Institute of Standards and Technology, 1991.
[4] Sun XQ, et al. Studies on smoke movement in stairwell induced by an adjacent compartment fire[J]. Applied Thermal Engineering, 2009, 29(13): 2757- 2765.
[5] Khoudja N. Procedures for quantitative sensitivity and performance validation of a deterministic fire safety model[D]. Texas: Texas A&M University, 1988.
[6] Peacock RD, et al. Issues in evaluation of complex fire models[J]. Fire Safety Journal, 1998, 30(2): 103- 136.
[7] Kong DP, et al. Uncertainty and sensitivity analyses of heat fire detector model based on Monte Carlo simulation[J]. Journal of Fire Sciences, 2011, 29(4): 317- 337.
[8] Albrecht C, Hosser D. A response surface methodology for probabilistic life safety analysis using advanced fire engineering tools[J]. Fire Safety Science, 2011,10: 1059- 1072.
[9] Suard S, et al. Sensitivity analysis of fire models using a fractional factorial design[J]. Fire Safety Journal, 2013, 62(B): 115- 124.
[10] Saltelli A, et al. Sensitivity analysis in practice: a guide to assessing scientific models[M]. New Jersy: John wiley&Sons, 2004.
[11] Xu CG, Gertner GZ. Uncertainty and sensitivity analysis for models with correlated parameters[J]. Reliability Engineering and System Safety, 2008,93(10): 1563- 1573.
[12] Morris MD. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991,33(2): 161- 174.
[13] McGrattan K, et al. Fire dynamics simulator technical reference guide volume 1: Mathematical model[M]. NIST special publication 1018, 2013.
[14] Harish R, Venkatasubbaiah K. Transport phenomena of turbulent fire spread through compartment connected to vertical shaft in tall building[J]. Fire Safety Journal, 2013, 61: 160- 174.
[15] Black WZ. Smoke movement in elevator shafts during a high- rise structural fire[J]. Fire Safety Journal, 2009,44(2): 168- 182.
[16] 许晓元, 等. 预测火灾情况下竖井中性面位置的连续模型[J]. 燃烧科学与技术, 2011, 17(4): 375- 381.
[17] 张靖岩. 高层建筑竖井内烟气流动特征及控制研究[D]. 合肥: 中国科学技术大学, 2006.
[18] Zhang W, et al. Turbulence statistics in a fire room model by large eddy simulation[J]. Fire Safety Journal, 2002, 37(8): 721- 752.
[19] DGJ 88- 2000, 上海市民用建筑防排烟技术规程[S].
[20] 张靖岩, 等. 高层建筑中利用竖井进行排烟的可行性分析[J]. 工程力学, 2006, 23(7): 147- 154.
[21] 李一帆, 等. 楼梯井顶部开闭状态对烟气运动的影响[J]. 燃烧科学与技术, 2013, 19(5): 464- 472.
[22] Huo R, et al. Introduction to building fire safety engineering[M]. Press of University of Science and Technology of China, Hefei, 1999: 116- 190.
[23] Mulholland GW. Smoke production and properties[J]. SFPE Handbook of Fire Protection Engineering, 1995, 3: 2- 258.
[24] Starr JW, LattimerBY. A comparison of IR stereo vision and LIDAR for use in fire environments[A]. in Sensors[C], IEEE, 2012: 1- 4.
Globalsensitivityanalysisoncharacteristicsofsmoketurbulenceandtransportinstairwellshaftwithstaircasestructureinahigh-risebuilding
XU Junru1, QIU Rong1, XIONG Caiyi1, JIANG Yong1, HUANG Yue2
(1. State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China; 2. Chongqing Municipal Fire Brigade, Chongqing 401120, China)
The cost for research on shafts in high- rise buildings is sometimes unaffordable due to the various factors associated with high- rise buildings and different effects of these factors. In this work, a global sensitivity analysis platform was constructed to investigate the effects of various factors quantitatively and offer a method to lower the computational cost by filtering out those factors with minuscule influence. In total 60 cases of high- rise building stairwell with staircase structures were simulated with numerical methods and then a hierarchy of effects of building structure sizes, heat release rate and ambient parameters on the characteristics of smoke turbulence and transport was derived from the computing results utilizing global sensitivity analysis. The sensitivity analysis results show that the effect ratios of heat release rate of fire source are above 38% to all the responses.
Stairwell shaft;Sensitivity analysis;High- rise building;Smoke;Neutral pressure plane
1004- 5309(2017)- 00147- 10
10.3969/j.issn.1004- 5309.2017.03.04
2016- 12- 15;修改日期2017- 04- 11
国家重点研发项目(2016YFC0801505);国家自然科学基金(51176181);高等学校博士学科点专项科研基金(20133402110010);中央高校基本科研业务费专项资金(WK2320000033、WK2320000035)
徐君儒(1991- ),男,安全科学与工程专业研究生,研究方向为高层建筑火灾及烟气蔓延数值模拟、火灾化学反应动力学模拟。
邱榕,E- mail: rqh@ustc.edu.cn
X932
A
