轿车轮毂轴承铆装工艺理论分析与试验研究
2017-12-29杨允松肖耘亚周志雄
杨 军 杨允松 李 伟 肖耘亚 周志雄
1.湖南大学机械与运载工程学院,长沙,4100822.韶关学院物理与机电工程学院,韶关,512005
轿车轮毂轴承铆装工艺理论分析与试验研究
杨 军1杨允松1李 伟1肖耘亚2周志雄1
1.湖南大学机械与运载工程学院,长沙,4100822.韶关学院物理与机电工程学院,韶关,512005
对轿车轮毂轴承单元的铆装工艺进行了理论分析和试验研究。建立了铆装力理论计算模型与铆装工艺有限元分析模型,研究了铆头轨迹、倾角和停留时间等工艺参数对铆装质量的影响,得出采用圆周轨迹、铆头倾角6°和停留时间0.8 s时铆装质量最好的结论。以DAC2F10轿车轮毂轴承单元为例,在课题组开发的铆合装配专用机床上进行了铆装试验,验证了铆装力理论模型和铆装工艺有限元模型的合理性,并进一步优化铆头倾角为5.5°。采用所优化的铆装工艺试制出了轮毂轴承单元样件,耐久性试验测试最高使用寿命近2×105km,表明得出的铆装优化工艺能大幅提高轮毂轴承单元的使用寿命和可靠性。
轮毂轴承;摆动碾压;铆合装配;工艺参数;使用寿命
0 引言
轮毂轴承单元是汽车的关键零部件之一,对汽车的安全性、舒适性、经济性等具有重要的影响[1]。轮毂轴承单元可分为6代,已进入商业化生产的是第3代和第4代,第5代和第6代已有报道但尚未获业界认可,而目前应用较为广泛的还是第3代。世界著名轴承公司如NSK、KOYO、SKF 等目前都已开发出了轴端铆装式的第3代轮毂轴承单元,其质量小,结构紧凑,使用寿命和可靠性都较高。而国内由于基础研究不足,关键的工艺装备与工艺技术落后,生产的轿车轮毂轴承单元可靠的使用寿命在1×105km以内,离2.5×105km的长寿命、高可靠性目标还有很大差距[2]。
国外虽已掌握轴端铆装式轮毂轴承单元的生产技术,但是出于各自的发展战略和利益竞争,对我国实行技术保密,所公开的文献资料大多是介绍相关结构设计优化和性能分析的,涉及核心铆装工艺及关键装备的则鲜见报道。如ISHIDA等[3]介绍了铆装式轮毂轴承单元的结构及开发要点。KAJIHARA[4]结合有限元仿真与试验测试研究了轮毂轴承单元的刚度、铆装接触面压力分布情况。MOON等[5]仿真研究了铆装时轴端的变形过程,测试了铆装力随铆装行程的变化情况。HYUNJIK等[6]、CHO等[7]分别采用二维模型和三维模型仿真研究了轮毂轴承单元的铆合装配过程,测试了铆装力和残余应变随铆装时间的变化情况。国内研究人员在轮毂轴承单元结构研究方面做了大量的工作。如WU等[8]分析了轮毂轴承单元的受力情况。华南理工大学谢小鹏教授团队对轮毂轴承单元的强度、刚度、使用寿命等进行了研究[9-11]。浙江工业大学王秋成教授团队对轮毂轴承单元的可靠性进行了研究[12-13]。黎桂华[14]研究了轿车轮毂轴承单元轴向游隙对轴承内外圈疲劳寿命及系统疲劳寿命的影响。而关于铆合式轮毂轴承单元的铆装工艺方面的研究,仅查阅到尹治国[15]仿真研究了铆头速度、轴端壁厚和高度、接触面摩擦因数等对卡紧力、内轴外径变化量及铆合形状的影响。
在轮毂轴承单元的生产中,通过铆合装配过程中工艺参数的优化控制可获得最佳的轴向卡紧力和工作游隙,进而大幅提高产品的使用寿命和可靠性。为此,本文首先建立铆合装配的理论分析模型;然后基于有限元模拟仿真,研究铆头轨迹、倾角、终铆停留时间等工艺参数对轴端铆合形状、轴端内孔和卡紧力的影响规律;最后,在课题组开发的轿车轮毂轴承单元铆合装配专用机床上进行了试验验证,以期通过理论分析、模拟仿真和试验验证相结合的方法为轿车轮毂轴承单元的铆合装配提供理论指导和工艺参考。
1 铆装工艺原理及理论分析
1.1 工艺原理
第3代轿车轮毂轴承单元是将外圈、内圈、滚动体、保持架等组件装配在一个单元中[7-8],传统的装配方式是采用螺母卡紧。近年来,随着对节能、可靠性和成本等要求的日益突出,在轿车轮毂轴承单元的装配方式上出现了以轴端铆装式取代螺帽卡紧式的趋势[9],如图1所示。轴端铆装式的优点在于:去掉螺母,减小了质量和尺寸,结构更加紧凑;铆装过程中可通过对工艺参数的控制获得稳定的轴向卡紧力,从而保证装配后获得较稳定的工作游隙,大幅提高其使用寿命和可靠性;消除了螺纹防松结构存在的卸载隐患,显著提高了产品的安全性。

图1 第3代轿车轮毂轴承单元Fig.1 3rd generation hub bearing unit
铆装式轮毂轴承单元的装配采用的是摆动碾压技术[15],具体是将倾斜的铆头(上模)在轴承单元内轴上滚动碾压,以使内轴的轴端受到局部压力并逐渐产生塑性变形,最终使组件牢固地连在一起并获得一个合适的轴向卡紧力和工作游隙,如图2 所示。因此如何通过控制铆装工艺参数来获得合适的工作游隙和轴向卡紧力是提高轴承使用寿命和可靠性的关键。

图2 轮毂轴承单元铆装工艺原理图Fig.2 Schematic diagram of riveting assembly of the hub bearing unit
1.2 理论分析
1.2.1接触面轮廓曲线方程
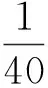
zcosγ-xsinγ=s
(1)
式中,γ为摆碾倾角。
铆头曲面方程为
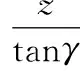
(2)
联立式(1)和式(2),可得接触轮廓曲线方程为
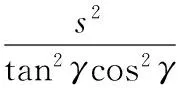
(3)
当γ=6°时,cos6°=0.995,当γ=10°时,cos10°=0.985,且由于铆头倾角一般小于10°,所以在本文中,当γ≠0时,cosγ≈1。
故接触轮廓曲线方程可简化为
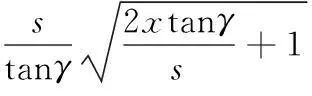
(4)
1.2.2接触面积系数
接触面投影面积如图2所示,以圆心O为极心建立极坐标,经坐标转换,忽略碾压中的径向变形,接触面积St为
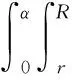
(5)
其中,ρ为极径,θ为转角,接触面外边弧转角α=arccos(1-θ),接触面内边弧转角α1=arccos(1-Rθ/r)。
接触面积与环形坯料上表面积之比为接触面积系数λ,具体为
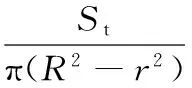
(6)
张猛[16]提出了环形件摆碾成形的接触面积系数简化公式:
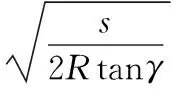
(7)
1.2.3铆装力
铆装力P为接触投影面积与作用在该面积上的单位压力之乘积,具体为
P=πλ(R2-r2)σK
(8)
式中,λ由式(7)求得;σ为碾压件材料屈服强度;K为摆碾系数,冷摆碾时,局部碾压变形方式的K值取1.6~1.9[17]。
由式(8)不难看出,在内轴材料确定的情况下,铆装力只与接触面投影面积有关。这是因为在铆装过程中,随着铆头的碾压进给,轴端材料逐渐产生径向流动,其与铆头的接触面积不断增大,如果需要轴端材料产生更大的塑性变形即径向流动,相应的铆装力也需不断增大,而铆头接触面积又受内轴结构尺寸、铆头形状尺寸、碾压轨迹及其倾角等因素影响。
2 铆装工艺参数影响仿真研究
模拟仿真分析在缩短产品开发周期,降低开发成本方面具有很大的优势[18-19]。为此,本文采用ABAQUS有限元分析软件对某轿车上第3代轮毂轴承单元进行铆装工艺分析。首先采用SolidWorks商用软件建立轮毂轴承单元和铆头的三维模型,将轮毂轴承单元、铆头三维模型导入ABAQUS有限元软件中并划分网格。铆装过程中,由于轴承单元的外圈、钢球及保持架等结构的影响较小,因此省去上述结构。所建立的轴承单元、铆头模型如图3所示,采用动力显式有限元模型分析。内法兰的材料为40Cr,其弹性模量为211 GPa,泊松比为0.277,材料密度为7870 kg/m3,屈服强度/屈服极限大于等于785 MPa;轴承内圈的材料为GCr15,其弹性模量为219 GPa,泊松比为0.38,材料密度为7830 kg/m3,屈服强度/屈服极限大于等于518.42 MPa[15]。由于轴端的塑性变形是铆装工艺的关键,为此对轴端区域的网格进一步细化,为减少模型运算量,将铆头定义为刚体。除将铆头划分为C3D10M单元外,轮毂轴承的单元类型均划分为C3D8R型,整个模型的网格总数为47 177个。
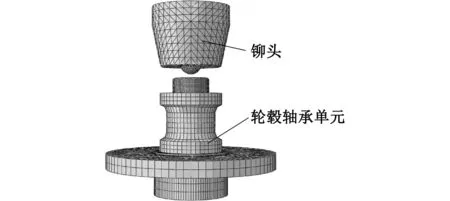
图3 轮毂轴承单元铆装有限元模型Fig.3 FE model of riveting assemb ly of the hub bearing unit
2.1 铆头轨迹

(a)圆周轨迹(b)多叶玫瑰线轨迹图4 圆周轨迹和多叶玫瑰线轨迹示意图Fig.4 Schematic diagram of circular and planetary motion
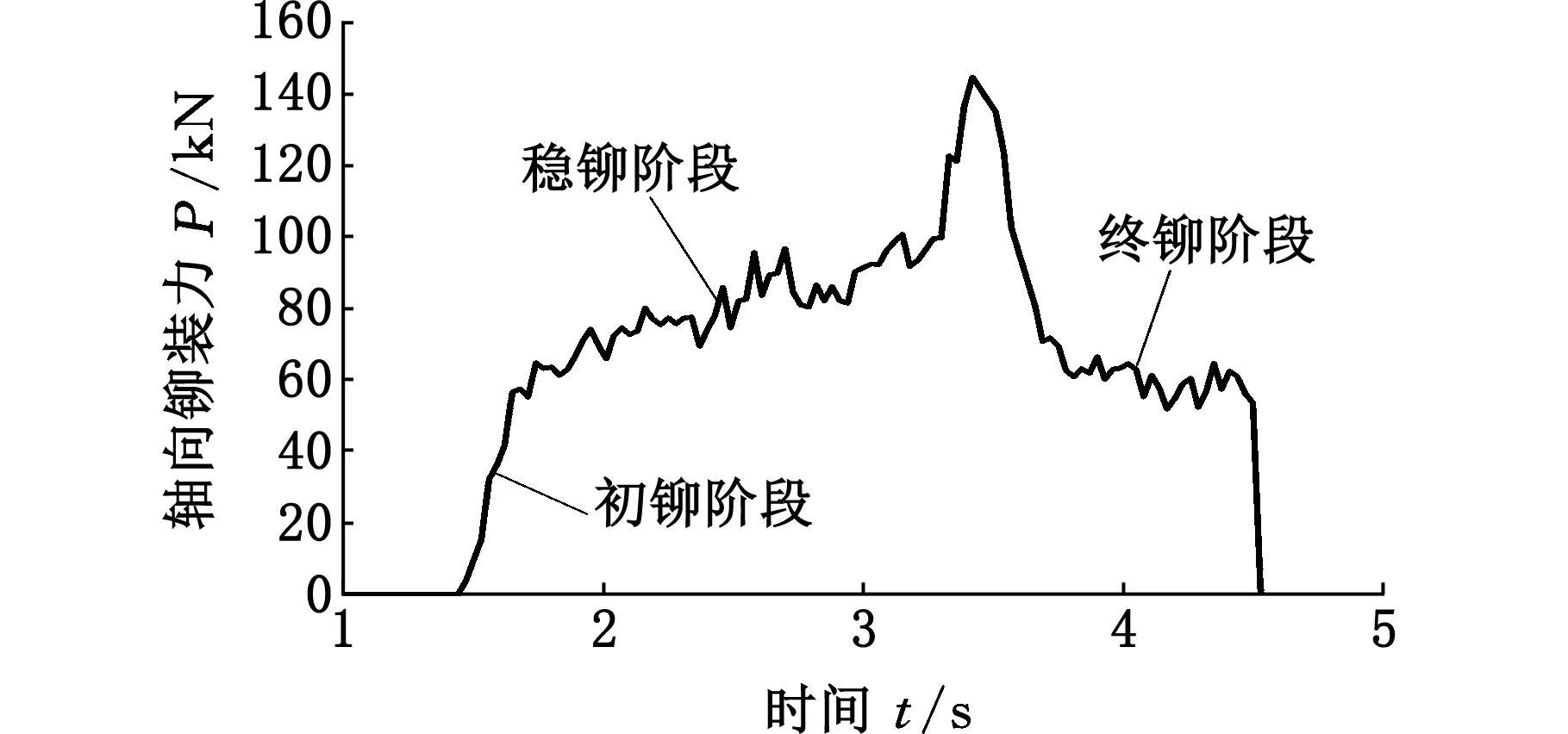
(a)圆周轨迹时的轴向铆装力
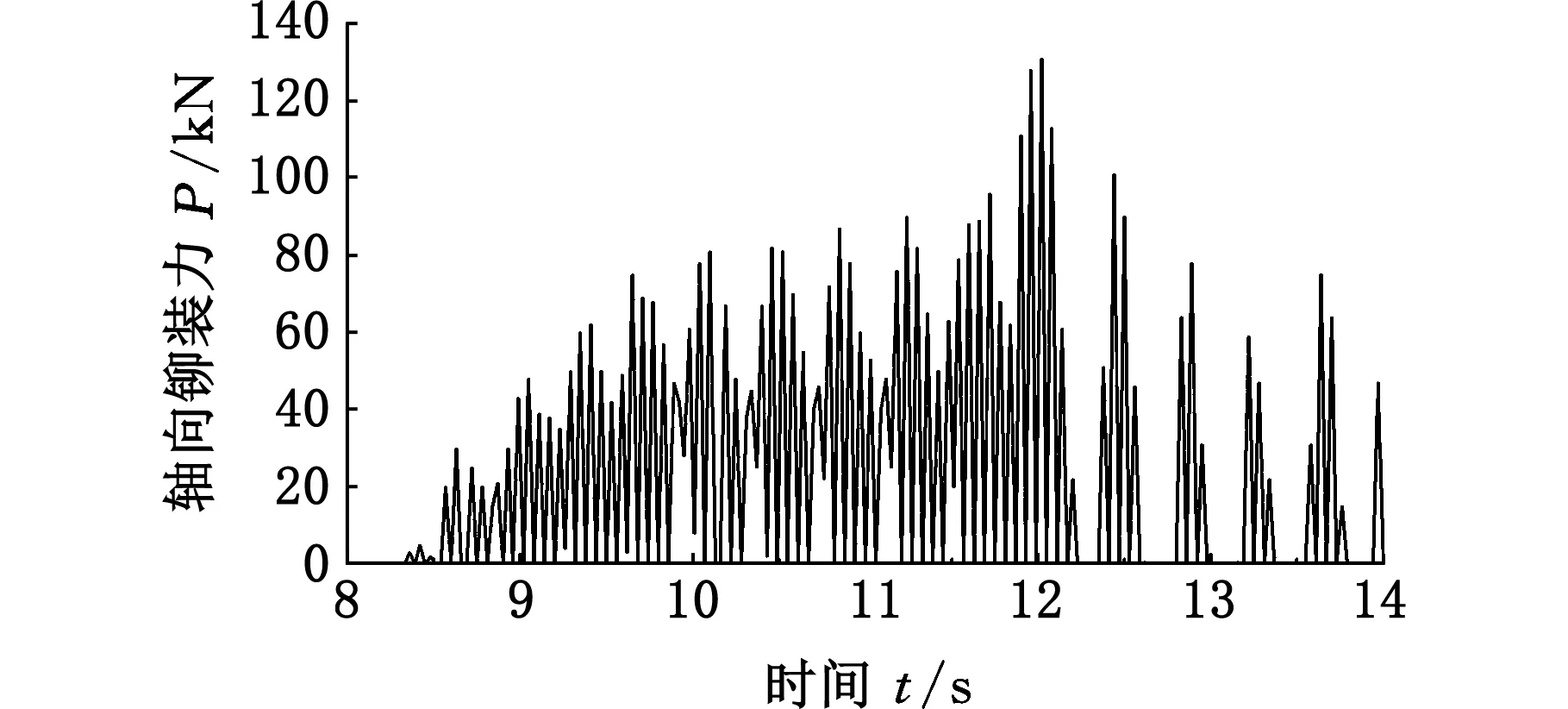
(b)多叶玫瑰线轨迹时的轴向铆装力[15]图5 轴向铆装力仿真计算结果Fig.5 Axial forming force of simulated results
在轮毂轴承单元铆装工艺中,铆头轨迹可采用圆周轨迹、多叶玫瑰线轨迹、直线轨迹、螺旋线轨迹和行星轨迹等,但是目前较为常用的还是圆周轨迹和多叶玫瑰线轨迹,如图4所示。本文研究了采用圆周轨迹时铆装力的变化规律,并与多叶玫瑰线轨迹时的轴向铆装力进行了对比分析,如图5所示。从图5可以看出,轮毂轴承单元的铆装工艺过程可以分为初铆(初始接触)、稳铆和终铆三个阶段。在初铆阶段,铆装力较快增大,这是由于铆头刚接触轴端时,轴端材料发生弹性变形;随着工件或铆头的继续进给,轴端材料进入塑性变形阶段,此时也开始进入轮毂轴承单元的稳铆阶段,铆装力较为稳定;当铆装快完成时,铆头往往还需要继续停留碾压,随后铆头与工件开始分离,此时铆装力快速下降,下降幅度远大于初铆时铆装力的增大幅度,这与轴端材料的少量弹性回复有关系(具体分析见2.3节)。同时,从图5中也不难看出铆装时采用圆周轨迹和多叶玫瑰线轨迹的铆装力变化规律并不相同。采用多叶玫瑰线轨迹铆装时的铆装力呈现近似于周期性波动变化规律,这实际上是由于按照多叶玫瑰线轨迹运动,铆头运动到中心处接触工件较少,而运动到叶瓣外端处碾压工件轴端,如此反复,从而造成铆装力的周期性波动变化。而采用圆周轨迹时,在铆装阶段铆装力总体平稳,但仍有逐渐增大的趋势,这是由于随着铆装的进行,工件材料接触面积及铆装体积逐渐增大,从而导致铆装力缓慢增大。而在稳铆阶段结束前,向终铆阶段过渡时,铆装力出现突变,迅速上升和下降,这可能是由于轴端材料已经与轴承内圈上表面接触,材料径向流动的阻力大大增加,变形更加困难所导致,但也不排除与计算模型有关,还需进一步分析研究。此外,采用圆周轨迹铆装时的整个工艺时间远小于采用多叶玫瑰线轨迹的整个工艺时间,这是因为采用多叶玫瑰线轨迹时铆头只有运动到叶瓣外端才碾压工件轴端。综合考虑铆装过程的平稳性及加工效率,本文采用圆周轨迹的铆合装配工艺。
2.2 铆头倾角
铆头倾角的大小不仅影响铆装时的径向力与轴向力,更重要的是会对轴端铆合形状有较大影响,如图6所示。铆装过程中,在铆头轴向进给行程相同情况下,若铆头倾角过小,铆头在圆周上旋转的幅度相对较小,就会使得凸缘翻边的金属材料径向流动不足,进而容易造成轴端材料变形不均匀,产生填不实、卡紧力不足的现象,从而使得铆装后的轮毂轴承单元可靠性差。若铆头倾角过大,会使得轴端材料随铆头旋转方向流动的幅度急剧增大,形成蘑菇效应,铆装过程稳定性比较差。同时,被铆轴端的塑性变形区也会变小变浅,从而使得轮毂轴承单元轴端顶部变形大而相邻内部膨胀变形小,造成铆装后的轴端与轴承内圈的结合较松。

(a)铆装倾角(0.5°)过小,铆装成形不足

(b)铆装倾角(8°)过大,铆装成形过度

(c)合理铆装倾角(5.5°)图6 不同铆装倾角下轴端的铆合形状Fig.6 Deformation of the revited shaft-end of different inclination angles
不合理的铆装倾角不仅影响轴端的铆合形状,而且还会在轴端因轴向压缩过大而使内孔产生缩孔现象,缩孔严重时会导致该轴承单元的内花键尺寸变小,从而使得轴承单元在与车轴装配时出现干涉。为此,在铆头轴向进给行程相同情况下,仿真得出了不同铆头倾角下被铆轴端内孔的孔径大小,如图7所示。轮毂轴承轴端内孔的初始孔径为16.00 mm,从图7中可以看出,被铆轴端内孔孔径随着铆头倾角的增大而减小,尤其是当铆头倾角大于6°后,被铆轴端的缩孔现象更为严重。这是由于随着铆头倾角的增大,铆头与轴端接触面逐渐转移到轴端上表面来,从而对轴端金属的轴向压力增大,进而造成径向扩张增大,内孔孔径也因此更小。
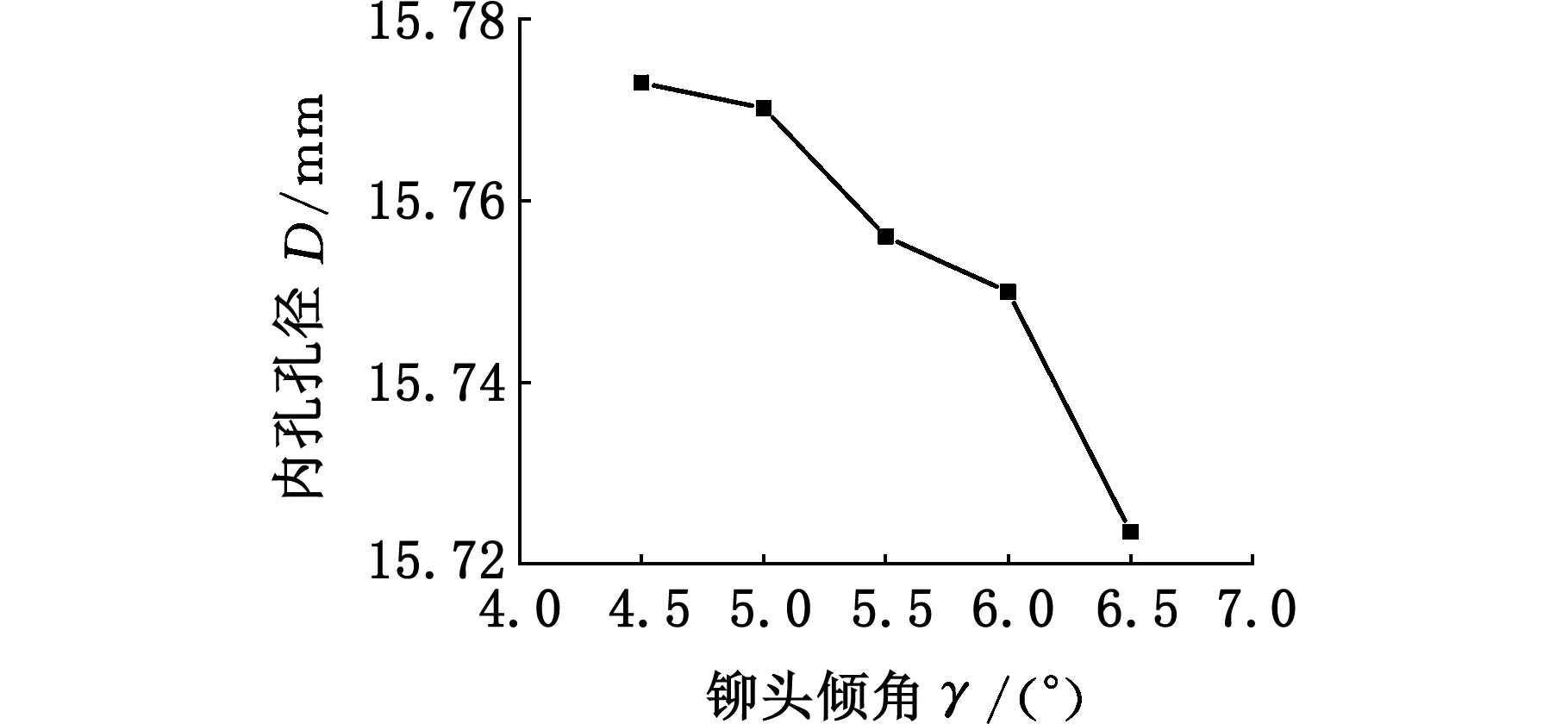
图7 不同铆头倾角下内孔孔径Fig.7 Correlation between pore size and inclination angle of the die
铆头倾角影响轴端铆合形状和内孔孔径大小,实际上更为关键的是由此会造成卡紧力的变化,而卡紧力是影响轮毂轴承单元使用寿命和可靠性的关键性因素。通过测量轴端与轴承内圈的被铆接触区域的接触应力导致的合力,可得出轮毂轴承铆装成形的预紧力,即卡紧力,如图8所示。仿真得出了不同铆合倾角下的卡紧力,如图9所示。从图9中可以看出,卡紧力随着铆头倾角增大呈现出先增大后保持稳定的变化规律,当铆头倾角在6°~6.5°时卡紧力达到峰值,并保持相对稳定的状态。
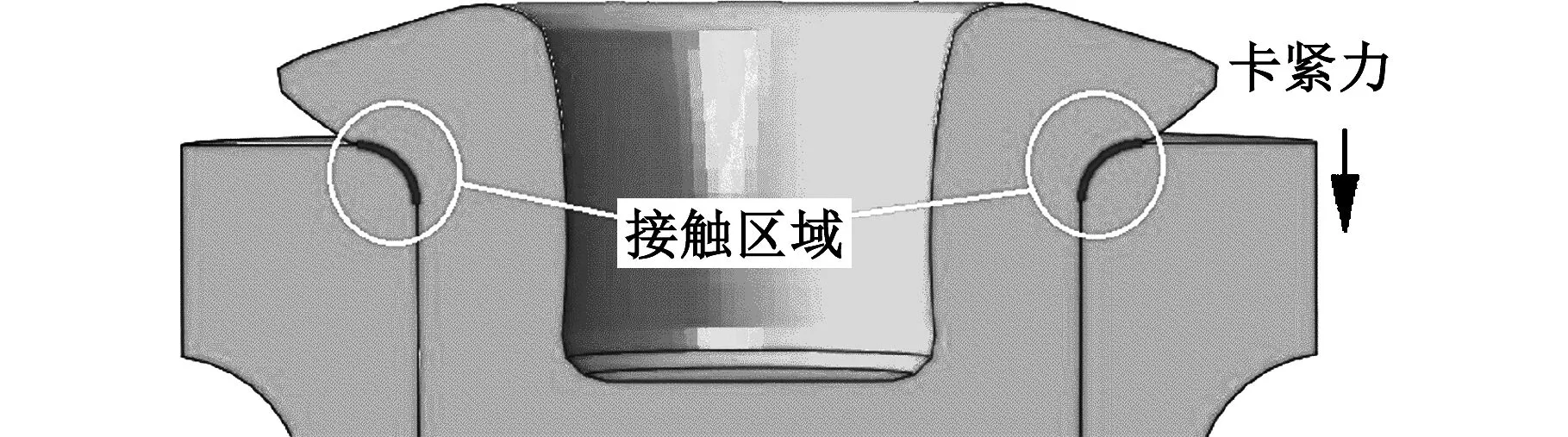
图8 被铆轴端与轴承内圈接触区域半剖图Fig.8 Schematic diagram of the cantact area of the inner bearing ring and the riveted shaft-end
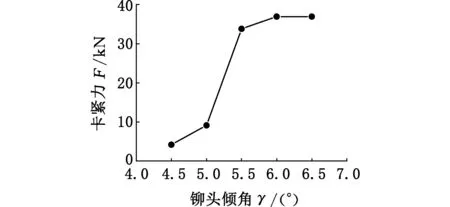
图9 卡紧力随铆头倾角的变化Fig.9 Correlation between chucking force and inclination angle of the die
铆头倾角的选取需要综合考虑轴端铆合形状、轴端内孔孔径及卡紧力。综上分析可以看出,当铆头倾角为6°时,轴端铆合形状较为合理,轴端内孔孔径变化较小,而卡紧力接近峰值且保持相对稳定。但是由于铆头倾角的大小对轮毂轴承单元的使用寿命和可靠性有着至关重要的影响,因此本文还将通过实际的铆装试验进一步验证并优化铆头倾角(见3.2节)。
2.3 铆头停留时间
轮毂轴承单元终铆后实际上还会出现弹性回复现象,该弹性回复不仅仅是由轴端材料的弹性变形造成的,铆装力作用在轴承单元组件的滚道上也会使各接触点处发生弹性变形,在铆装力下降时,这些弹性变形也都将回复。此时如果立即退回铆头,轴端材料与轴承组件所造成的总弹性回复会较大,从而难以形成所要求的卡紧力和工作游隙。因此,当铆头到达终铆点后,虽停止进给,但是还需继续碾压轴端,持续一定的时间后撤离,这样不仅可以保证轴端凸缘被碾平,更重要的是减小轴端的弹性回复,进而使轴承组件之间的弹性回复由于受到翻边凸缘的阻滞而无法完全回复,最终形成所要求的卡紧力和工作游隙。所以当铆头到达铆装行程终点后,还需对其停留时间进行优化。
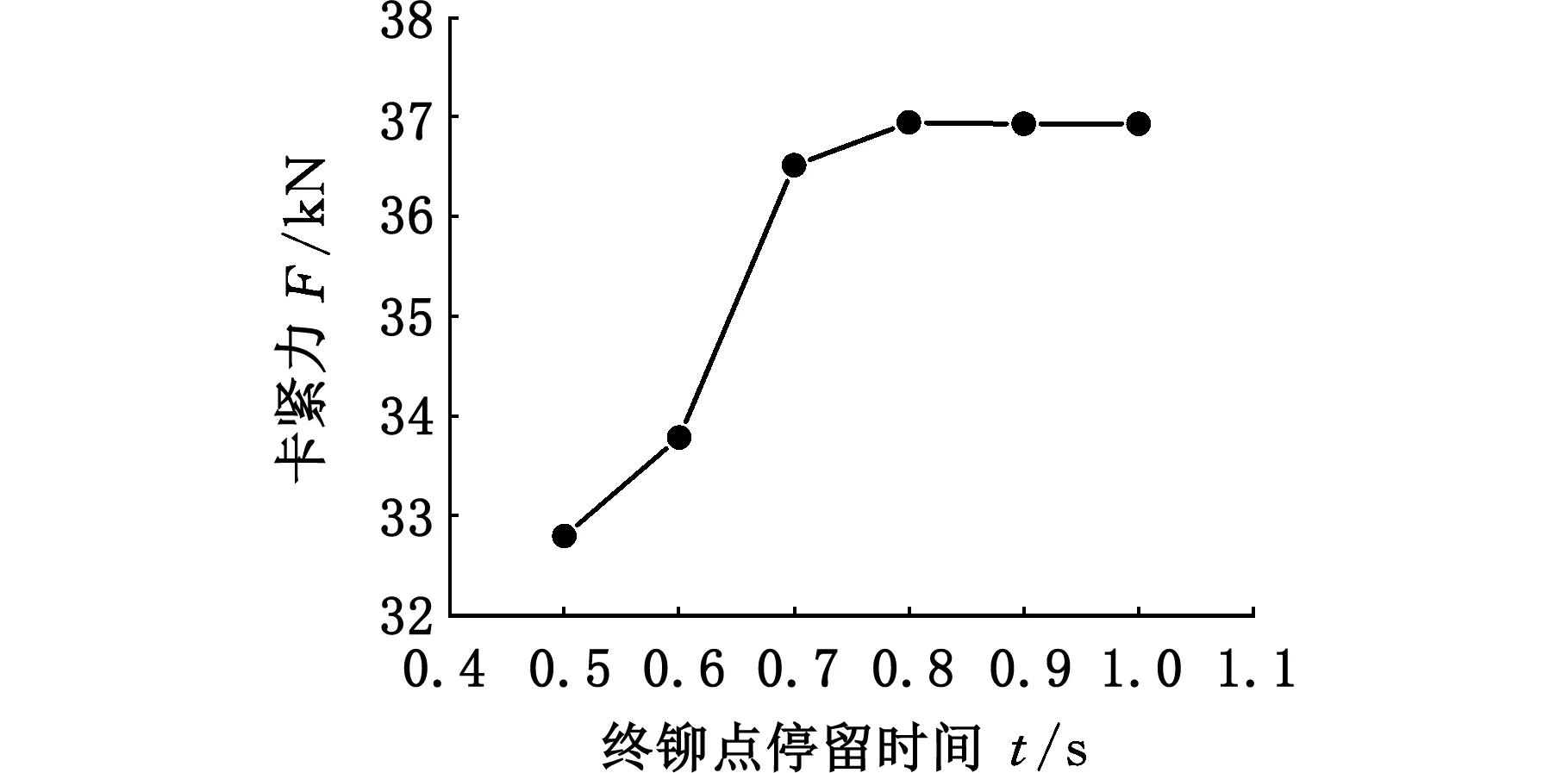
图10 不同铆头停留时间下的卡紧力Fig.10 Correlation between chucking force and different calibration time of the die
其他条件不变,改变铆头停留时间,发现轴端铆合形状基本相同,而内孔孔径虽有变化,但变化量很小,所以本文忽略了铆头停留时间对轴端铆合形状及其孔径的影响。但是从图10中可以看出,铆头停留时间对轮毂轴承单元的卡紧力却有较大影响。当铆头停留时间小于0.8 s时,卡紧力随铆头停留时间的延长而增大,这是由于终铆停止铆头进给后,原位停留的铆头仍保持着对轴端材料的压力,使其继续产生微小的塑性变形。随着铆头停留时间的延长,被铆轴端材料(40Cr)硬化程度逐渐增大,而且塑性不断下降,这就提高了材料在弹性阶段内的承载能力,且使其继续产生塑性变形的难度增大。当铆头停留时间达到0.8 s后,轴端不再产生塑性变形。所以停留时间不同,累积产生的微小塑性变形量就不同。铆头停留时间越短,卸载后翻边凸缘的弹性回复量就越大,残留的卡紧力就越小,铆头停留时间越长,弹性回复量就越小,残留的卡紧力就越大,但停留时间越过0.8 s后,弹性回复量不再发生变化,卡紧力达到相对稳定状态。
3 铆装工艺试验
铆装工艺试验在课题组开发的新型精密铆合装配专用机床上进行。该机床最大轴向铆合装配力达300 kN;铆头转速约720 r/min,并在0~10°倾角范围内连续可调;工作台的定位精度为-4~2 μm,最大工作行程为25 mm,在0~50 mm/s进给速度范围内连续可调;具备手动/自动铆合装配功能,生产效率可达3000件/班。
3.1 铆装力
采用圆周轨迹铆装DAC2F10轮毂轴承单元,测得铆装力随铆装时间的变化规律,并与理论计算、仿真结果进行对比,结果如图11所示。从图11中可以看出,在初铆、稳铆和终铆阶段,铆装力曲线的变化趋势基本一致,仿真得出的铆装力变化范围约为70~140 kN,试验得到的铆装力变化范围为102~121 kN,理论模型计算出的铆装力约为91.5 kN。理论模型计算结果与试验结果相比,误差范围为10.3%~24.4%。同时不难发现,该误差在刚进入稳铆阶段时最小,约10.3%,随着铆装工艺的进行而不断增大,稳铆结束时增大到24.4%,这是由于轴端与铆头接触初期,接触面积小,轴端成形的变形抗力小,随着铆装的进行,其变形抗力不断增大,所需的铆装力也因此增大,与理论计算结果误差逐渐增大。在终铆阶段,理论模型计算得到的铆装力几乎为0,这是由于在铆装力计算公式中进给量s近似于0,造成计算出的铆装力也近似于0。

图11 轴向铆装力试验结果Fig.11 Axial forming force of experimental results
3.2 铆头倾角
由2.2节分析可知铆头倾角的大小对轮毂轴承单元的使用寿命和可靠性有着至关重要的影响,为此试验研究了铆头倾角对铆装后轴端孔径大小的影响。图12为铆头倾角为1°时,铆装后轴端孔径的剖面图。由于铆头倾角过小,轴端轴向压缩过大,不仅缩径现象严重,而且轴端向外膨胀,严重时甚至可将小内圈挤裂,从而严重影响轮毂轴承单元的使用性能。

图12 铆头倾角1°时铆装后轴端变形图Fig.12 Schematic diagram of deformation of the shaft-end after reviting assembly when inclination angle of the die is one degree
为了进一步优化铆头倾角,设置工作台进给速度为3.2 mm/s,在机床上通过调整偏心套的周向位置来改变铆头倾角,并保持其他工艺参数不变,试验研究了不同铆头倾角下轴端缩径尺寸的变化,即轴端最大孔径与最小孔径及其两者之差,如图13所示。从图13中可以看出,在5.5°~6.5°范围内,随着铆头倾角的增大,缩径量(即最大孔径与最小孔径之差)先增大后减小,但是孔径的尺寸(即轴端最大孔径与最小孔径)却不断减小。当铆头倾角为5.5°时,缩径量最小,约为0.02 mm,远小于铆头倾角为6°时的0.05 mm,且最大孔径未发生明显变化。所以在后续加工中将铆头倾角由6°调整为5.5°。
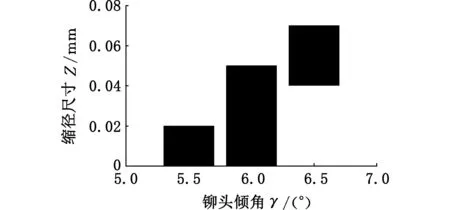
图13 不同铆头倾角下被铆轴端的缩径尺寸Fig.13 Pore sizes of different calibration time of the die
3.3 样件试制
以DAC2F10轮毂轴承单元为加工对象,根据理论分析、有限元仿真和工艺试验得出的铆头轨迹、倾角、停留时间等铆装工艺参数对轮毂轴承单元性能的影响研究结果,选取最佳工艺参数为铆头倾角5.5°、进给速度3.2 mm/s,铆头停留时间0.8 s,轴向铆装力约为120 kN,试制出了轮毂轴承单元样件,如图14所示。经耐久性试验测试,样件使用时间最长可达144 h,相当于行驶近2×105km(耐久性试验时间每7.25 h相当于行驶约1×104km)。

图14 试制的轮毂轴承单元样件Fig.14 Trial-manufacture sample of hub bearing unit
4 结论
(1)建立了轿车轮毂轴承单元铆装力理论计算模型,计算得出铆装力约为91.5 kN,与试验结果相比,误差范围为10.3%~24.4%。
(2)采用ABAQUS软件建立了轮毂轴承单元铆装工艺的有限元分析模型,仿真研究了铆头轨迹、倾角、停留时间对轮毂轴承单元性能的影响。考虑到生产效率及铆装稳定性,采用圆周轨迹铆装;综合考虑轴端铆合形状、轴端内孔孔径及卡紧力,选取铆头倾角为6°;当铆头停留时间大于0.8 s时,轮毂轴承单元的卡紧力达到相对稳定状态。
(3)试验研究了铆装力的变化及铆头倾角对被铆轴承孔径的影响,验证了轮毂轴承单元铆装力理论模型及铆装工艺有限元分析模型的合理性,并根据缩孔尺寸,将铆头倾角修正为5.5°。
(4)以DAC2F10轮毂轴承单元为加工对象,根据理论分析及试验结果选取的最佳铆装工艺参数为铆头倾角5.5°、进给速度3.2 mm/s、铆头停留时间0.8 s,轴向铆装力为105~122 kN,试制了轮毂轴承单元样件,经耐久性试验测试最高使用寿命近2×105km。
[1] SAKAMOTO J. Trends and New Technologies of Hub Unit Bearings[J]. NSK Motion & Control, 2005,17: 2-9.
[2] 肖耘亚. 轿车轮毂轴承单元摆碾铆合装配新工艺及设备的研究[D]. 长沙: 湖南大学, 2014.
XIAO Yunya. Research on New Process and Equipment for Precision Riveting and Assembly of Automotive Hub Bearing Units [D]. Changsha: Hunan University, 2014.
[3] ISHIDA H, KANEKO T. Development of Hub Unit Bearing with Swaging[J]. NSK Motion & Control, 2001,10: 9-14.
[4] KAJIHARA K.Improvement of Simulation Technology for Analysis of Hub Unit Bearing [J]. Koyo Engineering Journal English Edition, 2005,167E: 35-39.
[5] MOON H K, LEE M C, JOUN M S. An Approximate Efficient Finite Element Approach to Simulating a Rotary Forming Process and Its Application to a Wheel-bearing Assembly[J]. Finite Elements in Analysis and Design, 2007,44: 17-23.
[6] HYUNJIK C, JEONGSEO K. Orbital Forming Simulation of Automotive Hub Bearing Using the Explicit Finite Element Method[J]. International Journal of Modern Physics B, 2008, 22(9/11): 1626-1633.
[7] CHO H J, KOO J S, BAE W R, et al. A Study on Orbital Forming Analysis of Automotive Hub Bearing Using the Explicit Finite Element Method[J]. Transactions of the Korean Society of Automotive Engineers, 2008, 16(1): 29-36.
[8] WU Jia, LU Xiong. Load Analysis of Wheel Hub Bearing in Wheel Driving System with Exterior Rotor Motor[J]. Advanced Materials Research, 2012, 479/481, 670-675.
[9] 汪浔. 基于CAE 的轿车轮毂轴承单元刚性分析及试验研究[D]. 广州: 华南理工大学, 2011.
WANG Xun. Moment Rigidity Analysis on Whole Automotive Hub Unit Bearing Based on CAE and Its Research on Experiment[D]. Guangzhou: South China University of Technology, 2011.
[10] 卢小辉. 基于遗传算法的轿车轮毂轴承单元法兰盘轮毂优化设计[D]. 广州: 华南理工大学, 2011.
LU Xiaohui. Optimization Design on Hub Flange of Hub Unit Bearing Based on Genetic Algorithm[D]. Guangzhou: South China University of Technology, 2011.
[11] 杨林. 汽车轮毂轴承早期失效分析及试验研究[D]. 广州: 华南理工大学, 2012.
YANG Lin. Early Failure Analysis & Experimental Research of Automobile Wheel Hub Bearing[D]. Guangzhou: South China University of Technology, 2011.
[12] 张吉健. 汽车轮毂轴承的可靠性建模与试验技术研究[D]. 杭州: 浙江工业大学, 2009.
ZHANG Jijian. Study on Modeling Technique and Improving Reliability of Automobile Hub-bearing[D]. Hangzhou: Zhejiang University of Technology, 2009.
[13] 王露. 轮毂轴承多工况疲劳寿命建模与数值仿真[D]. 杭州: 浙江工业大学, 2009.
WANG Lu. Modeling & Numerical Simulation of Fatigue Lifeof Hub Bearing Based on Multi-bench Test Load[D]. Hangzhou: Zhejiang University of Technology, 2009.
[14] 黎桂华. 轴向游隙对轿车轮毂轴承性能的影响[J]. 轴承, 2011(1): 1-3.
LI Guihua. Effect of Axial Clearance on Performances of Car Hub Bearings[J]. Bearing, 2011(1): 1-3.
[15] 尹治国. 汽车轮毂轴承单元轴铆合过程仿真分析[D]. 广州: 华南理工大学, 2012.
YIN Zhiguo. CAE Analysis of Automotive Hub Unit Bearing Shaft-end Clinching Procedure[D]. Guangzhou: South China University of Technology, 2012.
[16] 张猛. 环形件摆动辗压力计算[J]. 热加工工艺, 1988(3): 15-21.
ZHANG Meng.Calculating Force in Rotary Forging Rings[J]. Hot Working Technology, 1988(3): 15-21.
[17] 伍太宾, 胡亚民. 冷摆辗精密成形[M]. 北京:机械工业出版社, 2011: 34-35.
WU Taibin, HU Yamin. Precision Forming of Cold Rotary Forging[M]. Beijing: Mechanical Industry Press, 2011: 34-39.
[18] 马俊林, 高仕恒, 李萍,等. 一种新型Al-Zn-Mg-Cu合金杯形件摆辗成形数值模拟及实验研究[J]. 中国机械工程, 2016, 27(7): 970-975.
MA Junlin, GAO Shiheng, LI Ping, et al. Numerical Simulation and Experimental Study on Rotary Roll Forging for a New Al-Zn-Mg-Cu Alloy Cup[J]. China Mechanical Engineering, 2016, 27(7): 970-975.
[19] 党玉功, 邓效忠, 王斌,等. 准双曲面齿轮冷摆辗加工新方法及其数值模拟[J]. 中国机械工程, 2014, 25(9): 1250-1255.
DANG Yugong, DENG Xiaozhong, WANG Bin, et al. A New Type Cold Rotary Forging Method for Hypoid Gear and Its Numerical Simulation[J]. China Mechanical Engineering, 2014, 25(9): 1250-1255.
TheoreticalAnalysesandExperimentalStudiesforRivetingandAssemblyProcessesofAutomotiveHubBearingUnits
YANG Jun1YANG Yunsong1LI Wei1XIAO Yunya2ZHOU Zhixiong1
1.College of Mechanical and Vehicle Engineering,Hunan University,Changsha,410082 2.School of Physics and Mechanical & Electrical Engineering,Shaoguan University, Shaoguan,Hunan,512005
The theoretical analyses and experimental study for riveting and assembly processes of automotive hub bearing units were conducted. The theoretical calculation model of riveting and assembly forces and the finite element analysis model of riveting and assembly processes were established to study the effects of trajectories, inclination angles and duration times of the final riveting phase of the rivet head on riveting and assembly quality. The results show the riveting and assembly quality is optimal under processing parameters including a circumference trace, an inclination angle of 6° and a final riveting duration time of 0.8 s of a rivet heat. Taking DAC2F10 automotive hub bearing unit as an example, it was assembled by the special machine tool developed by authors for riveting and assembly. The experiments show the theoretical calculation model of riveting and assembly forces and the finite element analysis model of riveting and assembly processees are rational. And the inclination angle of rivet head is optimized as 5.5°. The prototype automotive hub bearing unit is manufactured by the optimized riveting and assembly processes and the maximum service life examined by durability tests is nearly 200 000 km, which shows the optimized riveting and assembly processes herein may greatly enhance the working life and reliability of automotive hub bearing units.
hub bearing; rotary forging; riveting assembly; processing parameter; service life
2017-01-05
国家自然科学基金资助项目(51575358);广东省自然科学基金资助项目(2015A030313749)
TG306
10.3969/j.issn.1004-132X.2017.24.009
(编辑王艳丽)
杨军,男,1964年生。湖南大学机械与运载工程学院副教授。研究方向为切削磨削工艺与装备。发表论文10余篇。杨允松,男,1992年生。湖南大学机械与运载工程学院硕士研究生。李伟(通信作者),男,1983年生。湖南大学国家高效磨削工程技术研究中心讲师。E-mail: liwei@hnu.edu.cn。肖耘亚,男,1971年生。韶关学院物理与机电工程学院副教授。周志雄,男,1953年生。湖南大学机械与运载工程学院教授。
