永磁同步直线电机霍尔位置检测传感器的优化
2017-12-29李炳燃叶佩青
李炳燃 张 辉,2 叶佩青,2,3
1.清华大学机械工程系,北京,1000842.清华大学摩擦学国家重点实验室,北京,1000843.清华大学精密超精密制造装备与控制北京市重点实验室,北京,100084
永磁同步直线电机霍尔位置检测传感器的优化
李炳燃1张 辉1,2叶佩青1,2,3
1.清华大学机械工程系,北京,1000842.清华大学摩擦学国家重点实验室,北京,1000843.清华大学精密超精密制造装备与控制北京市重点实验室,北京,100084
针对采用线性霍尔元件检测直线电机动子的磁场进而通过磁场信息来解算电机位置的方法,通过介绍双霍尔传感器位置检测的原理,分析由安装误差造成解算位置偏差的机理。提出采用三轴霍尔传感器代替线性霍尔传感器的方法,实现霍尔线性影响因素的误差补偿。为了降低非线性干扰造成的位置解算误差,提出了模糊-神经建模方法来实现传感器的离线标定,最后通过仿真和实验证明了所提传感器误差补偿方法的有效性。
永磁同步直线电机;三轴霍尔传感器;位置检测;模糊控制
0 引言
永磁同步直线电机(permanent magnet synchronous linear motor, PMSLM)作为直线电机伺服系统中的核心部件,具有体积小、效率高、结构简单等优点[1]。相比于滚珠丝杠进给伺服系统,直线电机伺服系统将工作台与直线电机的动子刚性地连接在一起,消除了由机械传动环节所引起的摩擦、机械后冲、弹性变形等,因此直线电机伺服系统更容易获得较好的性能。
在直线电机伺服系统中,对电机动子位置的检测至关重要,电机所应用的位置传感器的检测精度直接影响电机的控制精度。文献[2-4]提出采用无位置传感器的电机位置检测方法,该种方法节约了电机制造成本,极大程度地简化了电机的结构,不过这种方法的检测精度和稳定性受到一定程度的限制[5-6]。而在位置控制精度较高的场合,光栅尺、拉杆位移传感器、LVDT等附加直线位移传感器被广泛应用,但是该类传感器造价高、体积大,附加的机械结构也会影响电机运动性能,所以它们在工程应用过程中受到了一定程度的限制[7]。
有学者提出使用线性霍尔元件检测电机动子磁场信息,通过该磁场信息解算电机动子的位置。该种方法具有制造成本低、安装方便、机械结构简单的优点。刘晓等[8]采用有限元的方法对圆筒型直线电机的气隙磁场进行了仿真和分析,并通过实验证明了霍尔元件选择合适的安装位置可以提高其检测精度。黄明等[9]考虑永磁体外围无法形成线性磁场分布的情况,提出了一种解决非线性测量问题的方案,实验结果表明采用合理的霍尔变送系统,可以提高系统的实时测量精度。徐丽莉等[10]同时采集霍尔传感器信号和电机动子的反电动势信号,通过两者之间的制约关系得到动子的相对位置,提高了霍尔器件的绝对检测精度。WEGENER等[11]分析了双霍尔传感器位置检测中不同种类干扰对检测结果的影响。刘刚等[12]针对霍尔传感器易受到高次谐波干扰的问题,提出一种采用正交锁相环来消除霍尔位置信号中高次谐波干扰的方法。
霍尔传感器在安装和使用过程中受到很多因素的干扰,这些干扰相互叠加在一起,使得电机检测精度降低。文献[12]将精度降低的原因总结为:①磁钢充磁不均匀以及磁钢形状参数不一致;②差分放大电路存在零点漂移;③环境温度的变化引起传感器温漂;④气隙磁场中含有各次谐波分量;⑤霍尔传感器存在安装误差。这些干扰因素间相互独立,可采用逐个分离干扰源并补偿的方式来提高电机的检测精度。
本文分析了霍尔传感器由于安装误差所产生的位置解算误差的原理,提出采用模糊控制的方法对霍尔传感器原始信号进行纠正,应用该方法提高了直线电机霍尔传感器的位置检测精度。
1 直线电机结构与霍尔传感器位置检测原理
永磁同步直线电机的结构如图1所示,主要包含电机定子、电机动子、绕组线圈等。电机动子的结构如图 2所示,其中τ为极距,两个霍尔元件安装在电机定子骨架上,在一定磁场强度范围内,霍尔传感器输出的电压与被检测区域磁通密度成线性关系。为了检测电机动子运动方向,通常安装两个相位差为90°的霍尔传感器,通过反正切函数解算出电机动子的位置,霍尔传感器的工作原理如图3所示。霍尔电压的计算公式如下:
UHα=KHIBcosα
(1)
式中,I为输入电流;B为磁感应强度;α为传感器与磁场夹角;KH为灵敏度系数。

1.电机定子 2.永磁体 3.电机绕组 4.定子外壳 5.导磁体 6.动子外壳图1 直线电机结构示意图Fig.1 Structure of linear motor
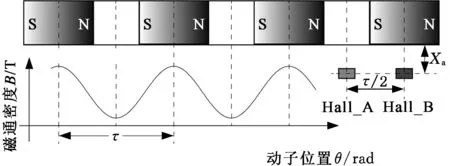
图2 霍尔传感器安装位置参数与动子磁场分布Fig.2 Position of Hall sensor and magnetic field distribution of the mover
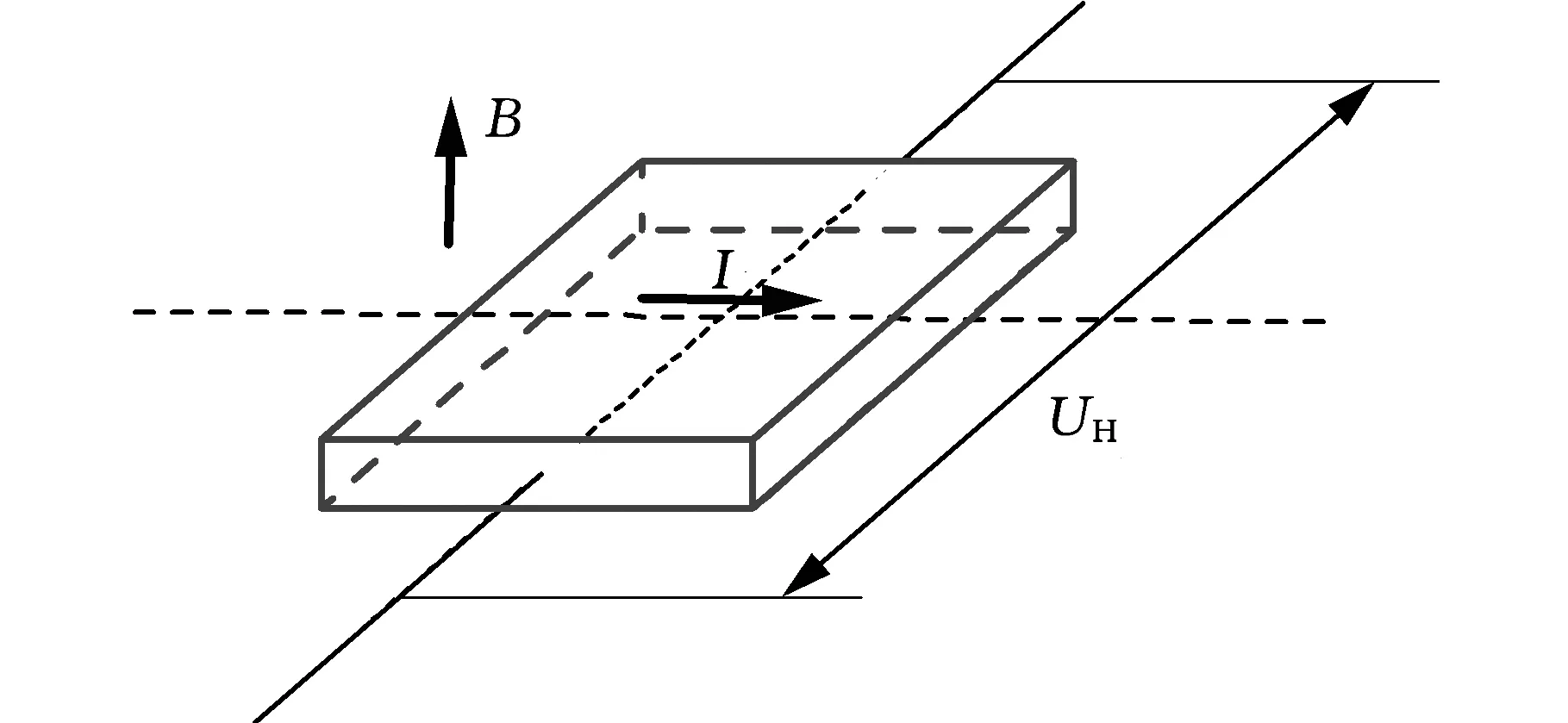
图3 霍尔元件工作基本原理Fig.3 Working principle of Hall element
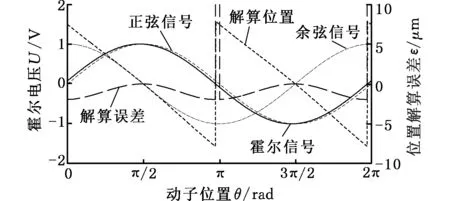
霍尔信号与动子位置关系如图4所示,霍尔传感器电压计算公式如下:
(2)
(3)
式中,A为增益系数;θ为动子位置。
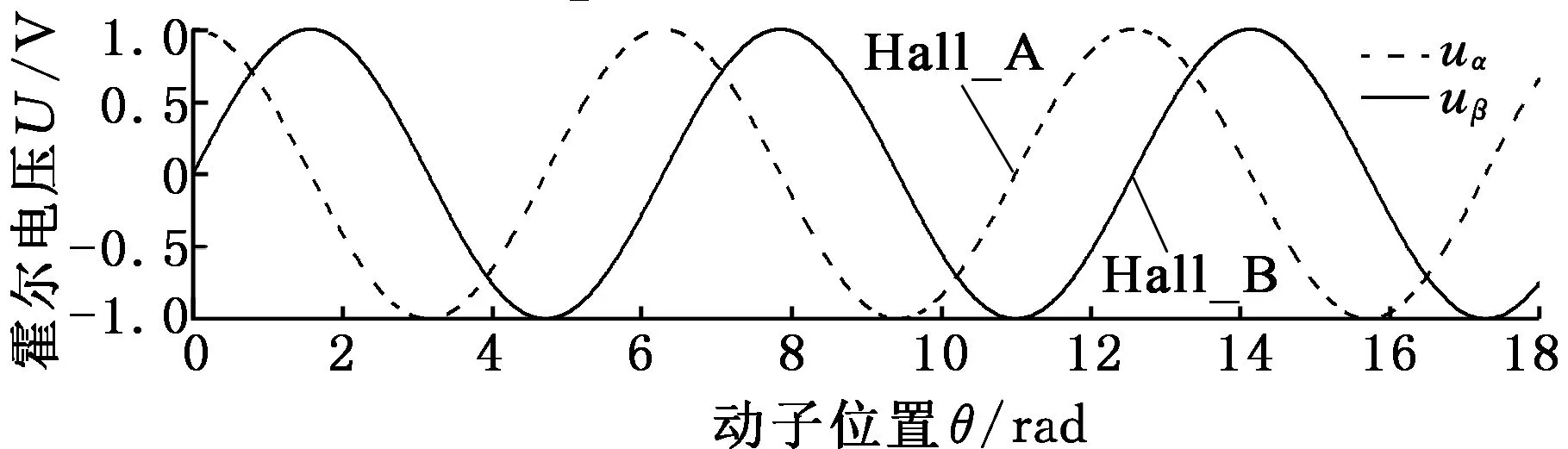
图4 霍尔信号与动子位置关系Fig.4 The relationship between the Hall signal and the position of the motor
2 霍尔传感器检测误差来源分析与简化
双霍尔传感器电机位置解算方法受到以下因素影响:uα和uβ的幅值是否相等;uα和uβ是否存在零偏;uα和uβ是否严格正交;uα和uβ是否是标准正弦函数。本文主要针对霍尔传感器安装误差导致的解算位置误差做定量分析,提出一种采用三轴霍尔传感器代替传统线性霍尔传感器的方法,以增强传感器安装误差的容错性,提高传感器的位置解算精度。
如果想准确检测电机的位置,必须保证以下安装要求:①两个霍尔元件必须严格与电机动子轴线水平;②两个霍尔元件必须在X轴方向保持高度严格一致;③两个霍尔元件在Y轴方向必须严格保证间距相差二分之一极距;④霍尔元件安装不允许存在角度误差。上述任何一个安装误差都会导致霍尔元件的解算位置结果不准确,而在现实情况中很难保证传感器有较高的安装精度,所以需要有一种误差检测与评价方法,对安装所产生的误差进行补偿。与此同时,由于传统霍尔元件检测的是垂直于传感器平面磁场强度的大小,对磁场方向的检测也依赖于传感器的安装基准面,所以在高精度磁场检测问题中,由安装位置偏差导致的检测误差不能忽略。
在建立位置偏差参数与检测误差结果的模型前,首先对空间位置偏差进行如下定义:
DX=Ra+Xa+ΔX
(4)
DY=ΔY
(5)
DZ=τ/2+ΔZ
(6)
(7)
其中,DX、DY、DZ为传感器距离磁场中心距离;Ra为动子直径;Xa为动子与传感器之间的安装间隙距离;ΔX为安装误差。其余位置参量见图5、图6。
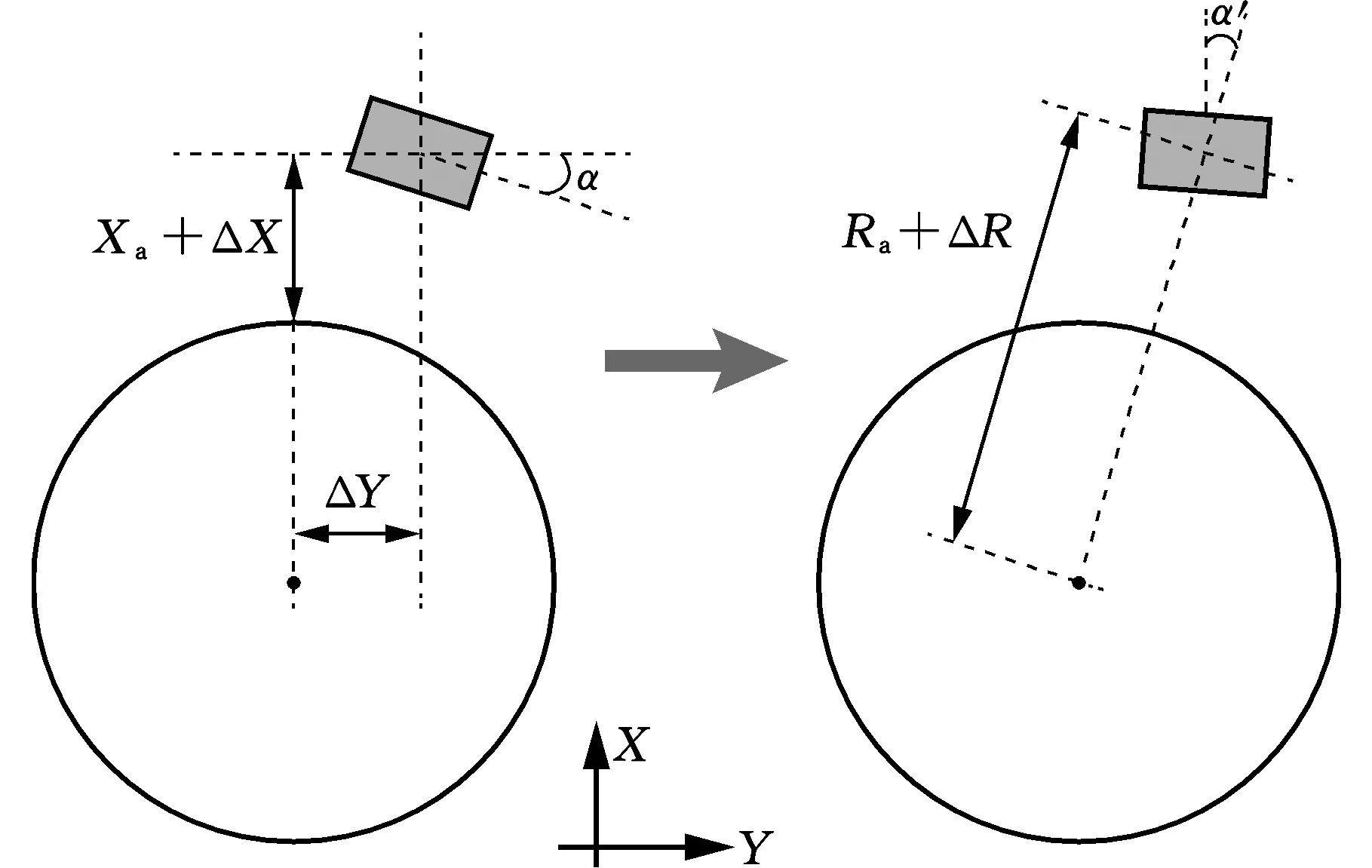
图5 XY平面上传感器位置参数Fig.5 Sensor position parameters on the XY axis
根据霍尔效应原理可知,沿着传感器垂直方向的是磁感线穿透的方向,其自旋角θγ不会影响传感器检测磁感应强度的大小,故θγ=Δγ,安装误差不会影响解算结果。若传感器安装位置存在θα=Δα、θβ=Δβ情况,传感器平面与所应检测磁场方向不互相垂直,则此时传感器输出电压为
UHα=KHIBαcos Δα
(8)
UHβ=KHIBβcos Δβ
(9)
电压幅值将会减小,这对解算电机位置的影响见下文数据仿真。
首先将XY平面的参数Xa+ΔX、ΔY、Δα进行简化。由于动子的磁场沿着半径方向呈现均匀放射状分布,所以可以将DX=Ra+Xa+ΔX、DY=ΔY用等效参数Dr=R+ΔR代替,表示其距离动子圆心的径向距离。相应地,θα=Δα转化为对应的转角误差θα′=Δα′。从而将参数DX、DY、θα化简为参数Dr和θα′。
再对XZ平面进行分析。由于DZ=τ/2+ΔZ的方向沿着电机运动方向,所以由安装误差ΔZ导致的位置解算误差可以通过相位差进行等效,同时ΔZ带来的误差与其他几个导致误差的因素相互不耦合,所以在此将这种情况单独处理。综上,影响位置检测精度的安装误差化简为Dr、θα′和θβ三个参数。
由于空间磁场畸变会使得霍尔传感器电压信号不是标准的正余弦形状,Dr和θβ的安装误差会在非线性范围内进行二次叠加,所以由Dr和θβ带来的位置解算误差呈现非线性。由于磁场垂直于霍尔传感器基准面的空间夹角误差θα′在位置解算误差中仅影响电压幅值大小,即θα′与电压幅值成线性关系,所以综合上面的化简过程,给出最终霍尔电压的安装位置参数模型为
UH=KHKαsin (α+δZ)
(10)
式(10)中,θα′影响系数Kα,ΔZ影响系数δZ,Dr和θβ影响信号的正弦性。下面通过仿真的方法获得各个影响因素对最终解算误差的影响程度。
假定Hall_B传感器得到信号为标准的余弦信号,Hall_A传感器分别给定三种情况的误差。图7a为受传感器幅值系数Kα影响的解算结果偏差曲线;图7b为传感器信号不为正弦信号,即受到Dr和θβ安装误差的影响曲线;图7c为两传感器安装相位偏差δZ的影响曲线。

(b)传感器信号不为正弦信号的影响
(c)两传感器安装相位偏差的影响图7 安装误差导致的解算误差分布Fig.7 Position error due to installation error
对三种情况下安装误差的偏离程度进行仿真对比,图8给出了安装误差由0增大到50%时三种误差源对最终解算结果误差的影响情况。可以看出相位安装误差对解算结果的影响最大,幅值不均等影响最小。
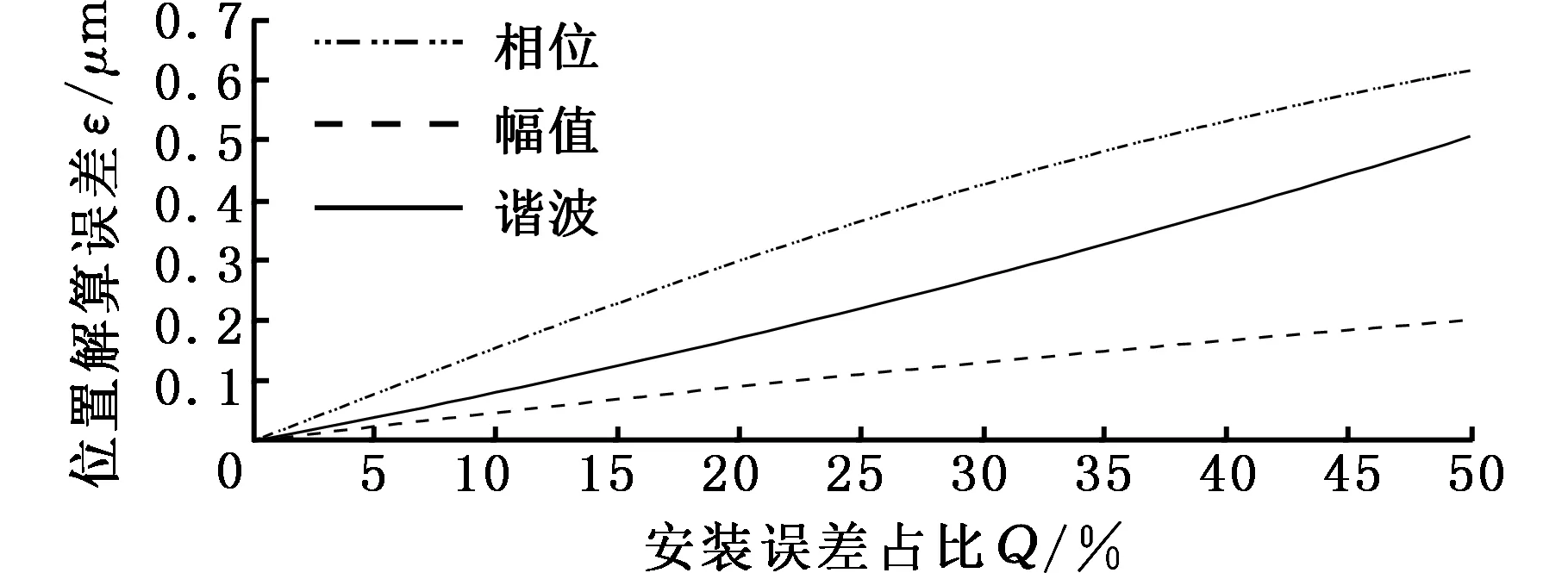
图8 安装误差大小与解算最大误差的关系Fig.8 Relationship between the size of the installation error and the maximum error
3 信号处理方法与模糊偏差纠正
本文通过分析受干扰信号的偏差来源与影响因素,得出各因素的影响效果与误差模型,本节将采用Fuzzy控制算法对存在偏差的霍尔信号进行位置矫正。通过实验获得标准动子位置与对应的霍尔传感器信号的数据,见图9,通过已有的数据训练一个Fuzzy神经元网络模型,从而获得一个误差矫正算法,将此算法应用到实时位置测量中,以补偿电机位置解算误差。

图9 霍尔传感器原始信号及其误差Fig.9 Hall sensor signal and errors
根据传感器信号利萨如图形(图10)可以看出,四个象限的误差趋势基本相同,但每个象限的误差呈现不规则变化。上述两个特点保证了采用相应的算法可以适当纠正传感器的偏差,该算法需要根据不同的输入数据推算出相应的误差等级,并对误差进行适当补偿。神经-模糊推理过程与模糊控制器结构如图11所示。
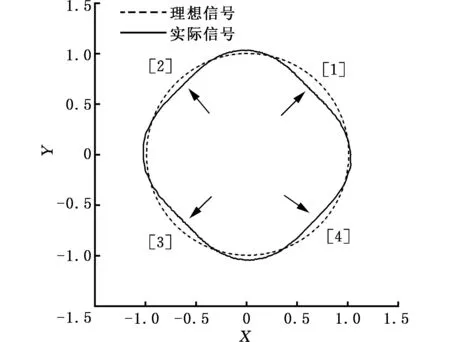
图10 霍尔传感器输出信号利萨茹图形Fig.10 Hall sensor output signal Leesa graphics
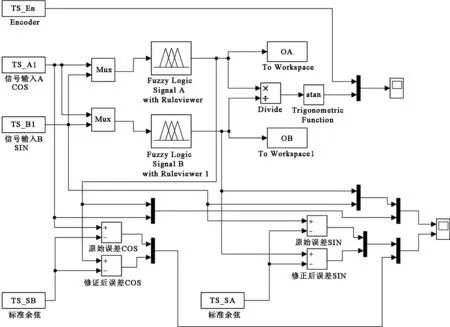
图11 神经-模糊推理过程与模糊控制器结构Fig.11 Neural-fuzzy reasoning process and fuzzy controller structure
本文采用基于神经元网络的模糊控制方案来提高传感器的绝对检测精度,通过多次采集传感器正余弦数据以及动子的绝对位置,以此作为学习数据对模糊控制模型进行迭代学习训练,最终得出模糊控制的训练模型,在MATLAB中进行计算验证,并通过LABView和MATLAB联合实现位置误差的在线解算和实时误差补偿。
4 实验方法与实验结果
实验平台包括一台微型直线电机,该电机动子由13节圆形永磁体组成,其长度为140 mm,定子内包含8组驱动线圈和两个霍尔传感器,其结构如图12a所示。电机设计最大加速度为10g,最大速度为200 mm/s,有效行程为120 mm,理论控制精度约20 μm。但由于电机传感器检测绝对位置的精度较差,通过带直线光栅尺检测装置的实验平台(图12b)测量,其实际位置检测误差最大值达300 μm。

(a)直线电机结构图

(b)实验平台结构图图12 直线电机结构图与实验平台结构图Fig.12 linear motor structure and experimental platform structure
实验平台中所用的位置检测装置为线性光栅尺,分辨率为1 μm,检测行程170 mm,输出信号格式为正交TTL信号,我们通过NI-6741高速脉冲计数卡对光栅尺位置进行记录,并通过模拟量采集卡同步记录霍尔传感器信号。该种方式可以同步获得霍尔传感器信号与标准的电机动子位置。
图13分别展示了无补偿算法情况下解算误差的情况和使用本文提出的模糊控制补偿方法后解算误差的情况。可以看出经过本文所提算法修正后的解算位置误差远小于未经处理的解算误差,证明了本文所提出算法的有效性。同时本文所提出的训练模型仅需在离线时使用光栅尺进行标定,在实际电机运行过程中,可通过简单的计算获得补偿后的数据,满足伺服系统对位置检测实时性的要求。
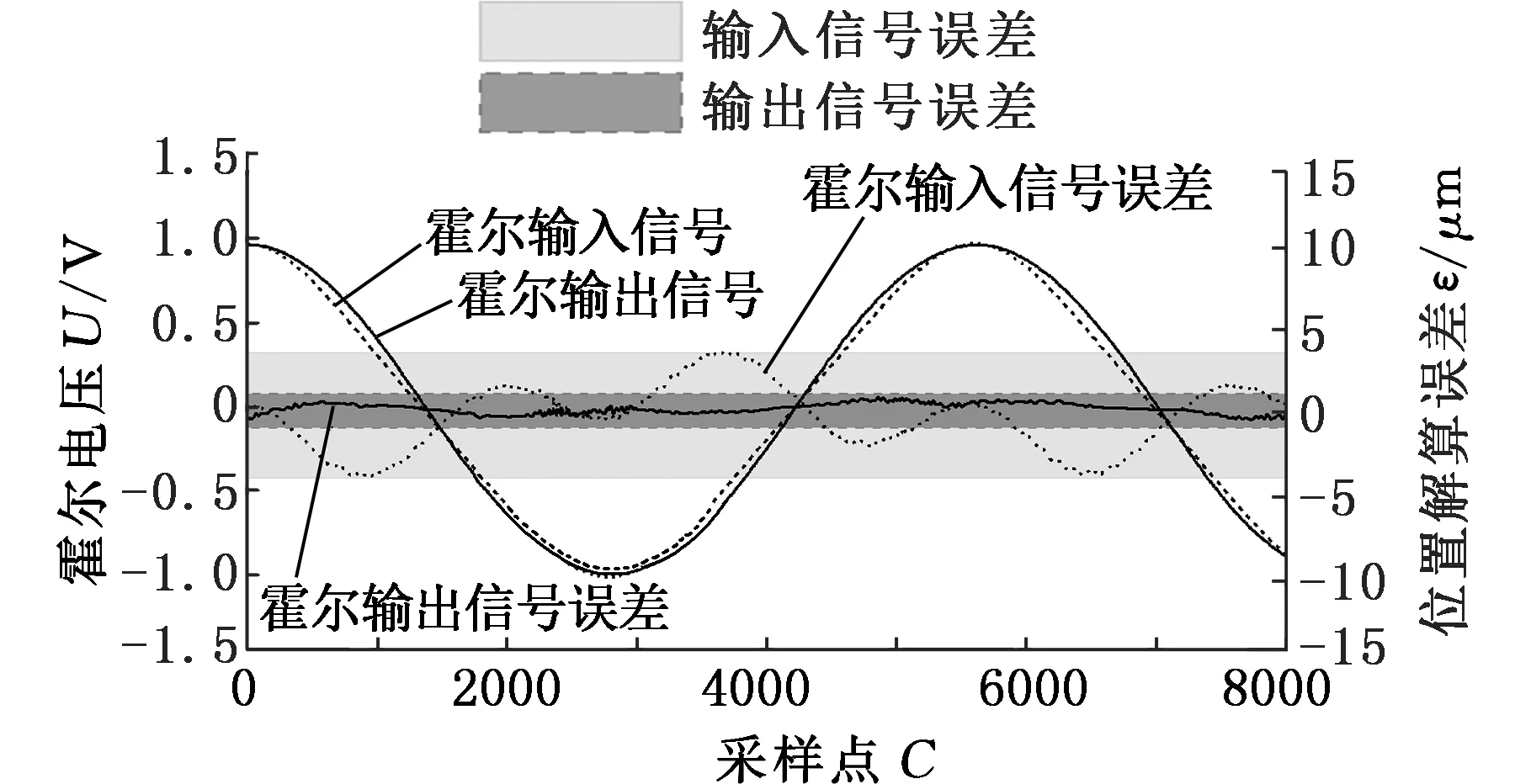
图13 补偿算法使用前后解算误差情况对比Fig.13 The results compared using the compensation algorithm
5 结论
(1)霍尔传感器安装位置偏差会影响其检测精度,其中一部分安装参数与输出的解算位置成线性影响关系,也有一部分安装参数与磁场非线性影响相互叠加,使解算位置误差增大。
(2)可以通过幅值纠正和相位补偿的方法对安装位置误差的线性影响部分进行纠正,而非线性部分的信号不能通过简单的算法进行纠正或补偿。采用三轴霍尔元件采集空间磁场,经过坐标变换可以得到准确的空间磁场分布,从而可以最小化非线性部分安装误差对信号的影响。
(3)采用神经-模糊推理控制器通过多次迭代学习,得到霍尔传感器信号与标准电机动子位置之间的误差关系,通过离线标定的方法得到误差补偿算法,并将该算法固化到位置解算过程中。此方法可以动态实时补偿由于信号不正弦性导致的结果偏差。本文通过仿真与实验,验证了该种位置检测误差补偿方法的可行性和有效性,提高了直线电机双霍尔位置检测的精度。
[1] SHIN K, LEE S, CHO H, et al. Analysis on the Pitching Moment in Permanent-magnet Linear Synchronous Motor for Linear Motion Stage Systems[J]. IEEE Transactions on Magnetics,2016,52:81049047.
[2] KANG J, ZENG X, WU Y, et al. Study of Position Sensorless Control of PMSM Based on MRAS[C]//IEEE International Conference on Industrial Technology. New York,2009:1-4.
[3] 丁文 ,梁得亮,罗战强. 两级滤波滑模观测器的永磁同步电机无位置传感器控制[J]. 电机与控制学报,2012,16(11):1-10.
DING Wen, LIANG Deliang, LUO Zhanqiang. Position Sensorless Control of PMSM Using Sliding Mode Observer with Two-stage Filter[J]. Electric Machines and Control,2012,16(11):1-10.
[4] 王丙元,冯辉. 基于定子电流的模型参考自适应感应电机转速估计[J]. 电机与控制学报,2013,17(9):48-56.
WANG Bingyuan, FENG Hui. Stator-current-based MRAS Estimaor for Insuction Motors[J]. Electric Machines and Control,2013,17(9):48-56.
[5] JUNG S Y, NAM K. PMSM Control Based on Edge-field Hall Sensor Signals through ANF-PLL Processing[J]. IEEE Transactions on Industrial Electronics,2011,58(11):5121-5129.
[6] SILVA C, ASHER G M, SUMNER M. Hybrid Rotor Position Observer for Wide Speed-range Sensorless PM Motor Drives Including Zero Speed[J]. IEEE Transactions on Industrial Electronics,2006,53(2):373-378.
[7] JEONG Y S, LORENZ R D, JAHNS T M, et al. Initial Rotor Position Estimation of an Interior Permanent-magnet Synchronous Machine Using Carrier-frequency Injection Methods[J].IEEE Transactions on Industry Applications,2005,41(1):38-45.
[8] 刘晓,叶云岳,郑灼,等. 一种低成本的线性霍尔位置检测方法研究[J]. 浙江大学学报(工学版),2008,42(7):1204-1207.
LIU Xiao, YE Yunyue, ZHENG Zhuo, et al. Low-cost Motor Position Detection Method by Linear Hall-effect Sensors[J]. Journal of Zhejiang University (Engineering Science),2008,42(7):1204-1207.
[9] 黄明,尚群立,余善恩. 线性霍尔传感器在直线位移中的应用[J]. 自动化仪表,2010,31(3):66-68.
HUANG Ming, SHANG Qunli, YU Shan’en. Application of Linear Hall Sensor in Linear Displacement Measurement[J]. Process Automation Instrumentation,2010,31(3):66-68.
[10] 徐丽莉,叶云岳. 基于线性霍尔元件的圆筒型永磁直线同步电机位置检测[J]. 微电机,2007(3):23-25.
XU Lili, YE Yunyue. Tubular Permanent Magnetic Linear Synchronous Motor and Its Position Detection[J]. Micromotors,2007(3):23-25.
[11] WEGENER R, SENICAR F, JUNGE C, et al. Low Cost Position Sensor for Permanent Magnet Linear Drive[C]// International Conference on Power Electronics & Drive Systems. New York,2007:1367-1371.
[12] 刘刚,肖烨然,宋欣达. 永磁同步电机用线性霍尔位置检测的误差补偿[J]. 电机与控制学报,2014,18(8):36-42.
LIU Gang, XIAO Yeran, SONG Xinda. Error Compensation of Rotor Position Detection for Permanent Magnetic Synchronous Motor Based on Linear Hall Sensors[J]. Electric Machines and Control,2014,18(8):36-42.
OptimizationofHallPositionSensorforPermanentMagnetSynchronousLinearMotors
LI Bingran1ZHANG Hui1,2YE Peiqing1,2,3
1.Department of Mechanical Engineering, Tsinghua University, Beijing,100084 2.The State Key Laboratory of Tribology, Tsinghua University, Beijing,100084 3.Beijing Key Lab of Precision/Ultra-precision Manufacturing Equipments and Control,Tsinghua University, Beijing,100084
There was a way to detect the positions of linear motors by detecting the magnetic field informations of linear motor movers. The principle of double Hall sensor position detection was introduced, and the cause of the installation errors was analyzed herein. In order to achieve the Hall sensor position detection error compensation, a method of using a 3D Hall sensor was proposed instead of a linear Hall sensor. In order to reduce external interferences, a fuzzy-neural off-line modeling method was proposed. Finally, the correctness of the compensation method was verified through the simulations and experiments.
permanent magnet synchronous linear motor(PMSLM); 3D Hall sensor; position sensor; fuzzy control
2016-10-31
国家科技支撑计划资助项目(2015BAI03B00);北京市科技计划资助项目(Z141100000514015)
TM383.4;TP212.9
10.3969/j.issn.1004-132X.2017.24.003
(编辑王艳丽)
李炳燃,男,1992年生。清华大学机械工程系博士研究生。主要研究方向为智能数控。发表论文4篇。E-mail:libingranzy@126.com。张辉,女,1969年生。清华大学机械工程系副研究员、博士研究生导师。叶佩青,男,1963年生。清华大学机械工程系教授、博士研究生导师。
