基于主成分分析方法的并联机构参数优化
2017-12-29曾达幸王娟娟樊明洲岳晓博侯雨雷
曾达幸 王娟娟 樊明洲 岳晓博 侯雨雷
燕山大学机械工程学院,秦皇岛,066004
基于主成分分析方法的并联机构参数优化
曾达幸 王娟娟 樊明洲 岳晓博 侯雨雷
燕山大学机械工程学院,秦皇岛,066004
以DELTA并联机构为研究对象,求解该机构的全域条件数、全域各向同性系数、全域最小奇异值指标数据,建立多维全域性能指标数据。基于主成分分析(PCA)法,对上述多维全域性能指标数据进行降维、有效融合,去除指标间的冗余信息,减小目标函数对权重系数的人为依赖性,从而确定目标函数。通过对不同结构参数样本进行PCA分析,选出基于综合全域性能最优的结构尺寸。将PCA优化结果与各性能指标值分布图进行比较分析,最优和最差样本均与各性能指标分布图的最优和最差性能区域相对应,从而验证PCA方法在并联机构参数优化时的有效性。研究结果为多目标下并联机构的优化提供了一种新思路。
参数优化;并联机构;主成分分析;全域性能指标
0 引言
随着并联机构应用领域的不断深入与拓展,对其性能指标的要求也愈加全面。根据实际工况任务的需求,对机构进行优化成为影响设计优劣的关键。目前并联机构多基于单一指标进行参数优化,如黄田等[1]基于全域灵活度实现对球面并联机器人的尺度综合;刘辛军等[2]基于传动角,定义了一种关于力/运动性能传递的度量指标,并对PVRRRPV(P和R分别表示移动副和转动副,下标V表示移动副P的运动方向是竖直方向)并联机器人进行机构参数的优化设计。而在机构实际应用中往往需要考虑多指标之间的相互影响,希望基于多指标选出满意的机构结构尺寸,因此机构的参数优化应该是多目标优化问题。多目标优化问题的传统分析方法(如主要目标法、权重系数法等)是将多目标问题变为单目标优化问题,从而使多目标优化成为可能,但此类方法并不是真正意义上的多目标优化[3]。智能仿生算法(如遗传算法、粒子群优化算法、神经网络算法等)是基于群体进行优化,已被应用于多目标优化中[4-6]。机构的参数优化还有一种方法是性能图谱,该方法是在有限的空间内用图形表示性能指标与设计参数之间的关系,但得到的最佳结果往往是模糊的。
主成分分析(principal component analysis,PCA) 法[7]是统计学中一种多元统计方法,该方法充分考虑各指标间的信息重叠,在进行数据简化的同时能够最大程度地保留原有信息,更客观地确定各个指标的权重,避免了主观随意性。目前,PCA法已应用到水质监测[8]、环境质量评价[9]、人脸识别[10-11]、机械故障特征融合[12-13]和诊断[14]以及工业数据中的去噪[15]等领域。文献[16]将PCA法应用于同一构型不同尺度平面2R机械臂和三种不同构型空间3R机械臂运动灵活性综合评价。文献[17]应用PCA法和核主成分分析(kernel principal component analysis,KPCA)法对不同尺度的PUMA560串联机器人的全域性能进行综合评价。文献[18]基于不同工作任务,使用PCA法和KPCA法对平面2-RR并联机构的综合性能进行评价和比较分析。目前PCA法在并联机构参数优化方面的应用相对较少。
本文应用PCA法对并联机构参数进行优化,以典型的DELTA并联机构为研究对象,给定不同的结构参数样本,基于运动学全域性能指标,运用PCA法通过综合性能评分得出性能最优的结构参数样本,开展机构参数优化。而后绘制各性能指标值分布图,与PCA法优化结果进行对比分析,最优和最差样本均在各性能指标值分布图的最优和最差区域内,从而验证PCA法的有效性。
1 DELTA并联机构全域性能指标确立
DELTA并联机构是目前应用最成功的三自由度并联机构之一,如图1所示,该机构是由定平台、动平台和三条均布并包含有平行四边形结构的支链组成。
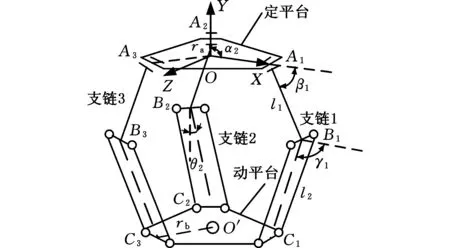
图1 DELTA并联机构简图Fig.1 Simplified structure of DELTA parallel mechanism
DELTA机构的基本尺寸如下:定平台外接圆半径为ra,圆心为O,动平台外接圆半径为rb,圆心为O′,AiBi(i=1,2,3)长度为l1,BiCi长度为l2。OAi与定坐标系OXYZ的X轴正向之间的夹角αi分别为0°、120°、240°,AiBi与定坐标系的OXZ平面之间的夹角为βi,平行四边形机构与定坐标系的OXZ平面之间的水平面转角为γi,平行四边形机构与定坐标系OXYZ的Y轴负向之间的夹角为θi,定平台与动平台相互平行。
Bi、Ci点在定坐标系中的坐标为
由BiCi=l2,可得表达式如下:

(1)
xi=rcosαi+l1cosαicosβiyi=-l1sinβi
zi=-rsinαi-l1sinαicosβi
r=ra-rbi=1,2,3
由式(1)可得

(2)
i=1,2,3
对式(2)进行一阶泰勒展开,并对时间求导得
(3)
式(3)转换为矩阵形式,有
令
则可简化为
则该机构的雅可比矩阵为
(4)
根据式(4)可求出DELTA机构的雅可比矩阵。并联机构的灵活性指标解析式多数与雅可比矩阵有关。确立全域条件数x1、全域各向同性系数x2、全域最小奇异值x3为优化指标,对DELTA机构进行优化,这三项性能指标解析式都是基于雅可比矩阵求得,但是所具有的物理意义不同,在不同方面反映了并联机构的灵活度。各全域性能指标具体信息如表1所示。
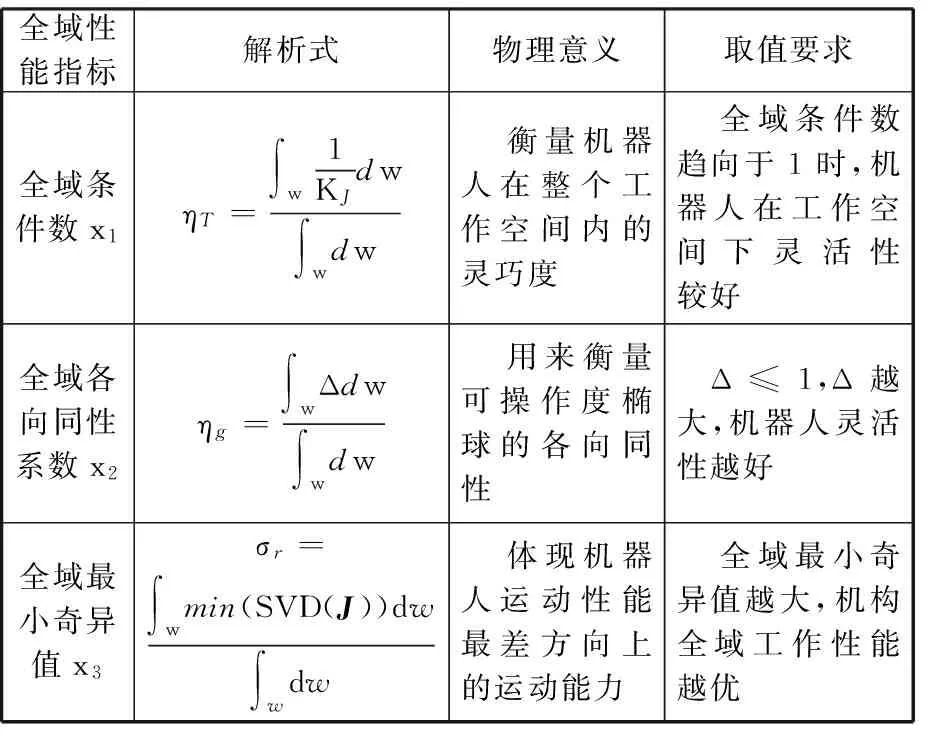
表1 全域性能指标具体信息
表1中,w为机构工作空间;min(SVD(J))为雅可比矩阵J的最小奇异数;KJ为条件数,Δ为各向同性系数,其表达式分别为
KJ=‖J‖·‖J-1‖
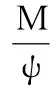
式中,m为机构操作空间维数;λi(i=1,2,…,m)为雅可比矩阵J的特征值。
2 DELTA并联机构主成分分析过程
2.1 DELTA并联机构结构参数量纲一化
为把DELTA并联机构多维无限尺寸空间变换到有限的三维空间中来,从而可以系统地研究机构尺寸与性能的关系,将DELTA机构结构尺寸进行量纲一化,即
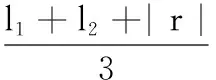
(5)
量纲一化后的DELTA机构结构尺寸为

(6)
由式(5)、式(6)可得
r1+r2+r3=3
为使DELTA机构满足组装和运动要求,需满足条件
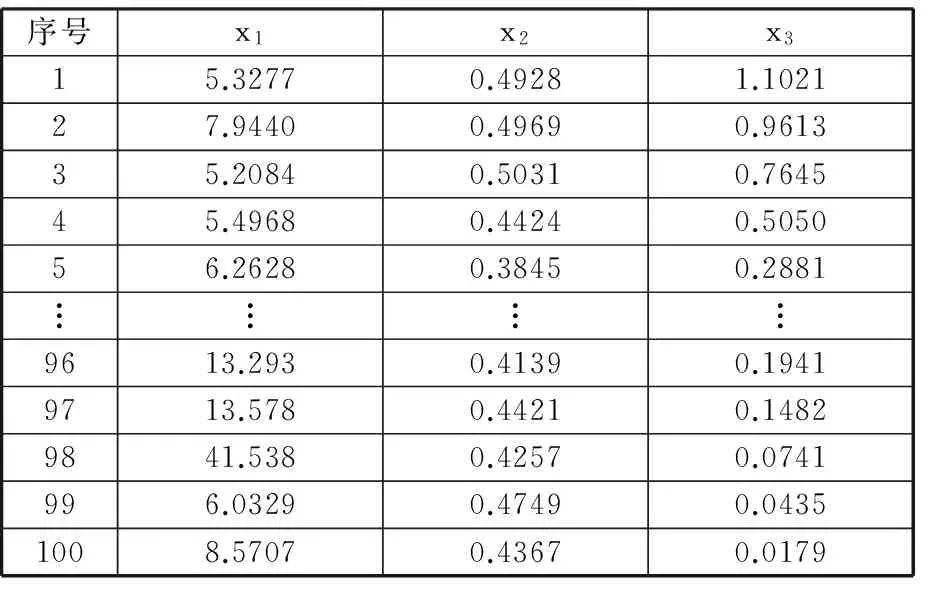
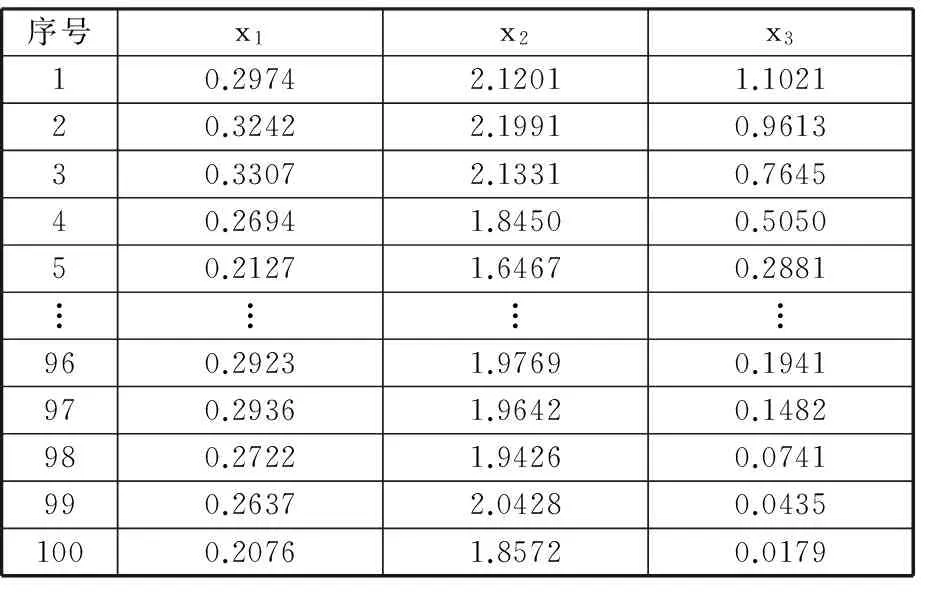
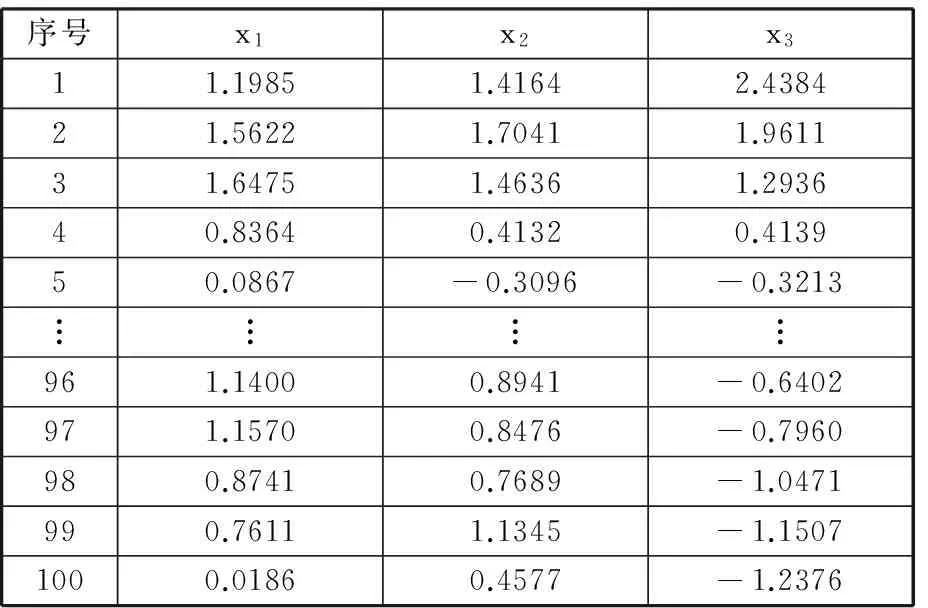
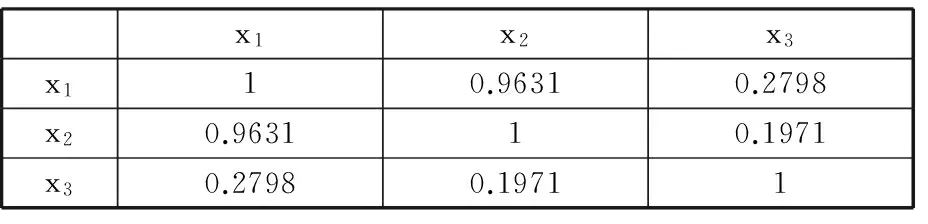
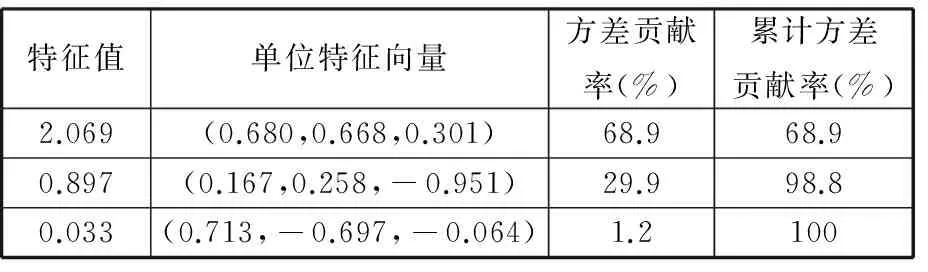
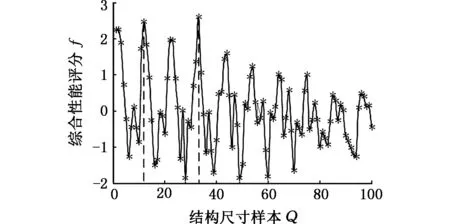
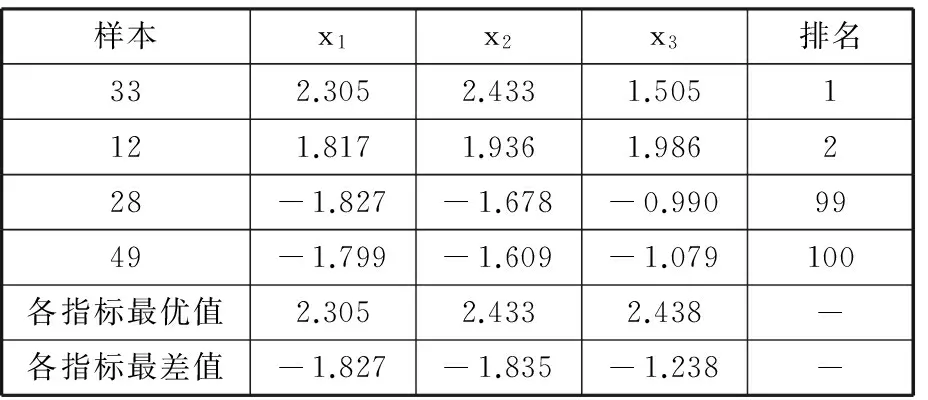
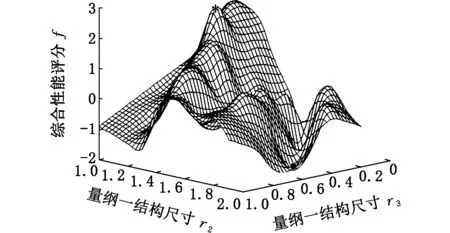
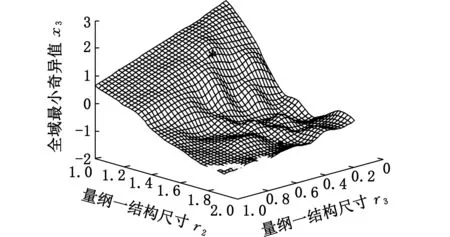
0 根据表1中的解析式求得各指标原始数据,构成原始样本矩阵X如下: X由m个不同尺寸的DELTA并联机构样本的n个全域性能指标构成。 根据表1中相应的解析式,利用MATLAB编程,求取每个样本的全域条件数x1、全域各向同性系数x2和全域最小奇异值x3,构成样本的指标原始数据。选取100个参数样本,其具体数值如表2所示。 表2 DELTA机构性能指标原始数据 各性能指标原始数据随尺寸改变会产生不同的优劣趋势变化。指标x3是正向指标,其值越大,机构所对应性能就越好。指标x1、x2为适度指标,其值越接近1,机构所对应性能越好。为了便于分析,在数据分析之前,先将数据正向化处理,使各指标变为正向指标。正向化公式为 x′=1/|x-t| (7) 式中,t为指标最佳值。 利用式(7)对x1、x2作正向化处理,正向化后的性能指标数据如表3所示。 表3 DELTA机构正向化后性能指标数据 各指标的量纲和数量级不同,指标数据之间不具有可比性,需先将数据标准化处理,使各指标数值都处于同一个级别上,从而便于进行综合测评分析。 采用Z-Score变换对正向化后的性能指标数据进行标准化处理,得到样本标准化后的数据矩阵Z,其具体数值如表4所示。 标准化公式为 其中 表4 DELTA机构标准化后性能指标数据 灵活性指标之间存在一定的相关性,使数据存在一定的信息重叠,应用相关系数可以充分反映灵活性指标间的相关性,这是降维的首要条件[15]。 矩阵Z的相关系数矩阵为 (8) 根据式(8),其具体数值如表5所示。由表5可知,x1与x2的相关系数为0.9631,相关系数较大,相关性较强。x1与x3相关系数为0.2798,x2与x3相关系数为0.1971,相关系数较小,相关性较弱。由此可知,三个指标相互之间的相关程度不同。相关系数矩阵反映了各性能指标间的内部联系。主成分则是基于指标之间这些内部联系而确定的。 表5 相关系数矩阵 求取矩阵R的特征值以及单位特征向量。每一个单位特征向量所对应的特征值代表了相关系数矩阵在这一单位特征向量上的贡献率(即能量)。由主成分的数学模型和统计特征知,主成分Fi的方差为R的第i大特征根λi,故各主成分方差贡献率表示包含原始信息能量的多少,其方差贡献率为 选取主成分的原则是不丢失主要信息,而衡量信息的指标是主成分的方差,方差越大,说明包含主成分的信息量越大[19]。将特征值λi(i=1,2,…,n)进行排序:λ1≥λ2≥…≥λn。各特征值对应的单位特征向量为 vi=(vi1,vi2,…,vin)Ti=1,2,…,n 根据特征值的累计方差贡献率Mi来确定主成分个数k,通常取累计方差贡献率大于或等于85%[20]。其前p个主成分累计方差贡献率Mi为 (9) 由式(9)可计算主成分的累计方差贡献率,PCA分析过程中具体信息如表6所示。由表6可知,第一主成分累计方差贡献率为68.9%,该值小于85%,不满足确定主成分条件;第一主成分和第二主成分方差贡献率达到98.8%,该值大于85%,故确定主成分个数为2。 表6 样本PCA分析计算结果 第一主成分能代表指标x1、x2的信息,第二主成分则主要代表指标x3的信息。将特征根对应的单位特征向量作为主成分模型中的权重系数,确定主成分表达式,这样就排除了人为设定参数计算过程的干预,保证了评价过程中的客观性。 主成分的数学模型为 Fi=ei1Z1+ei2Z2+…+einZn (10) 其中ei=(ei1,ei2,…,ein)T为Fi的系数向量。多元统计学已经证明,ei是R特征根λi对应的特征向量vi[19]。现选取两个主成分,由式(10)得第一主成分表达式为 F1=0.680Z1+0.668Z2+0.301Z3 (11) 第二主成分的表达式为 F2=0.167Z1+0.258Z2-0.951Z3 (12) 根据各指标的权重系数,结合各指标的具体物理意义,若主成分Fi越大,机构的灵活性能越好,则主成分Fi正向;若主成分Fi非正向,则需对主成分Fi进行正向化处理[21]。对式(12)可进行正向化处理,即 (13) PCA法根据相关系数矩阵反映的信息,求取其特征值和单位特征向量,客观地赋予各指标权重系数,对并联机构进行综合性能评价。构造并联机构综合性能评价函数: (14) 则由式(11)~式(14)得DELTA机构的综合性能评价函数表达式为 (15) 选取的性能指标都是反映DELTA机构灵活性的指标,故综合性能评分越高,代表DELTA机构的灵活性能越好。根据式(15),绘制得出100个样本PCA优化结果图谱,10个样本为一组,如图2所示。 图2 PCA优化结果图谱Fig.2 Atlas of optimization results by PCA method 由图2可知,每组样本的综合性能评分大致趋势为先增后减,规律相似。各组样本的最高评分宏观上也呈先增后减的趋势。综合性能评分最高的是样本33,该样本具体信息如表7所示。 得分排名第2的样本是样本12,得分排名第99的样本是样本28,得分最低的样本是样本49。样本33、12、28、49性能指标对比如表8所示。 表7 样本33具体信息 表8 4个样本性能指标值与各性能指标极值对比表 由表8可知,在所有样本的全域条件数x1中,样本33的x1是最优值,样本12的x1接近最优值,样本28的x1是最差值,样本49的x1接近最差值。在所有样本的全域各向同性系数x2中,样本33的x2是最优值,样本12的x2接近最优值,样本28和样本49的x2较为相近,且接近最差值。在所有样本的全域最小奇异值x3中,样本12比样本33的x3更接近最优值,样本49比样本28的x3更接近最差值。由以上分析以及表5可知,各指标不会在同一样本中同时出现最优值。最优样本33和最差样本49的各个性能指标值与所对应的性能指标最优值和最差值也极为接近,表明了PCA方法优化的有效性。 为了更为直观地验证PCA法优化的有效性,绘制出该DELTA机构的综合性能评分三维图和各性能指标值分布图,见图3和图4,图中*为最优样本33,•为最差样本49。 图3 综合性能评分三维图Fig.3 Map of comprehensive performance score 观察图3和图4可知,图3综合性能评分三维图与图4a、图4b单个性能指标值的分布图相似但不相同,图3所呈现的效果是图4a~图4c三者的结合。由图4可知,x1与x2的指标值分布图相似度较高,x1和x3、x2和x3的指标值分布图相似度较低。在各性能指标值分布图中,最优样本33位于性能优秀的样本区域内,最差样本49位于性能较差的样本区域内。由此验证了PCA法在DELTA并联机构参数优化应用中的有效性。 (a)全域条件数x1 (b)全域各向同性系数x2 (c)全域最小奇异值x3图4 DELTA并联机构各性能指标值分布图Fig.4 Distribution map of the performance index values of DELTA mechanism (1)将主成分分析法应用于DELTA并联机构的参数优化,克服了性能图谱方法优化结果不唯一的弊端;通过求取各指标之间的相关系数以及相关系数的特征值和特征向量,确立主成分,进而确立目标函数,得出综合性能评分最高的样本结构尺寸,对并联机构尺度综合具有指导意义。 (2)通过对主成分分析法优化结果以及各性能指标值分布图的对比和分析,验证了优化结果的有效性。本研究是对并联机构综合性能优化方法的扩展,可为不同构型并联机器人机构多目标优化提供新的思路。 [1] 黄田, 曾宪菁, 倪雁冰,等. 球面并联操作机的尺度综合方法[J]. 自然科学进展, 2000, 10(8): 751-756. HUANG Tian, ZENG Xianjing, NI Yanbing, et al. The Dimensional Synthesis of Spherical Parallel Manipulator[J]. Progress in Natural Science, 2000, 10(8): 751-756. [2] 刘辛军, 吴泽启, 张立杰. 基于力传递性能的一种平面并联机器人的优化设计[J]. 清华大学学报(自然科学版), 2008, 48(11): 1751-1754. LIU Xinjun, WU Zeqi, ZHANG Lijie. Optimum Design of a Planar Parallel Robot Based on Force Transmissibility[J]. Journal of Tsinghua University (Science and Techonlogy),2008, 48(11):1751-1754. [3] 赵亮, 雎刚, 吕剑虹. 一种改进的遗传多目标优化算法及其应用[J]. 中国电机工程学报, 2008, 28(2): 96-102. ZHAO Liang, JU Gang, LYU Jianhong. An Improved Genetic Algorithm in Multi-objective Optimization and Its Application[J]. Proceedings of the CSEE, 2008, 28(2): 96-102. [4] 侯媛彬, 薛斐, 郑茂全, 等. 基于多层编码的遗传-粒子群融合算法流水线优化控制[J]. 机械工程学报, 2015, 51(9): 159-164. HOU Yuanbin, XUE Fei, ZHENG Maoquan, et al. Optimization of Flow-shop Control by Using Genetic-particle Swarm Algorithm of Multilayer-coded[J]. Journal of Mechanical Engineering, 2015, 51(9): 159-164. [5] SCHMIDHUBER J. Discovering Neural Nets with Low Kolmogorow Complexity and High Generalization Capability[J]. Neural Networks the Official Journal of the International Neural Network Society, 1997, 10(5): 857-873. [6] 张渝, 胡启国, 张甫仁. 基于粒子群算法的冷挤压模具结构参数优化设计[J]. 中国机械工程, 2010, 21(8): 1003-1007. ZHANG Yu, HU Qiguo, ZHANG Furen. Optimal Design of Structural Parameters of Cold Extrusion Dies Based on Partical Swarm Optimization[J]. China Mechanical Engineering, 2010, 21(8): 1003-1007. [7] KURODA M,MORI Y, LIZUKA M, et al. Acceleration of the Alternating Least Squares Algorithm for Principal Components Analysis[J]. Computational Statistics and Data Analysis, 2011, 55(1): 143-153. [8] 黄姗, 丁坚平, 徐洋. 基于主成分分析法对开阳县岩溶地下水水质的评价[J]. 环保科技, 2014, 20(6): 48-52. HUANG Shan, DING Jianping, XU Yang. The Evaluation of Karst Groundwater Quality Based on Principal Component Analysis in Kaiyang[J]. Environmental Protection and Technology, 2014, 20(6): 48-52. [9] 刘臣辉, 吕信红, 范海燕. 主成分分析法用于环境质量评价的探讨[J]. 环境科学与管理, 2011, 36(3): 183-186. LIU Chenhui, LYU Xinhong, FAN Haiyan. Study of Applying Principal Component Analysis to Environmental Quality Assessment[J]. Environmental Science and Management, 2011, 36(3): 183-186. [10] 周桐. 基于PCA的人脸识别系统的设计与实现[D]. 哈尔滨: 哈尔滨工业大学, 2007. ZHOU Tong. Face Recognition System Design and Implementation Based on Principal Component Analysis[D]. Harbin:Harbin Institute of Technology, 2007. [11] 王婧瑶, 许勇, 曹本希. 基于主成分分析的超声人脸识别算法研究[J]. 计算机工程与设计, 2013, 34(8): 2867-2871. WANG Jingyao, XU Yong, CAO Benxi. Ultrasonic Face Recognition Algorithm Based on Principal Component Analysis[J]. Computer Engineering and Design, 2013, 34(8): 2867-2871. [12] 古莹奎, 杨子茜, 朱繁泷. 基于主成分分析的齿轮故障特征融合分析[J]. 中国机械工程, 2015, 26(11): 1532-1537. GU Yingkui, YANG Zixi, ZHU Fanlong. Gearbox Fault Feature Fusion Based on Principal Component Analysis[J]. China Mechanical Engineering, 2015, 26(11): 1532-1537. [13] 古莹奎, 承姿辛, 朱繁泷. 基于主成分分析和支持向量机的滚动轴承故障特征融合分析[J]. 中国机械工程, 2015, 26(20): 2778-2783. GU Yingkui, CHENG Zixin, ZHU Fanlong. Rolling Bearing Fault Fusion Based on PCA and SVM [J]. China Mechanical Engineering, 2015, 26(20): 2778-2783. [14] NGUYEN V H, GOLINVAL J C. Fault Detection Based on Kernel Principal Component Analysis[J]. Engineering Structures, 2010, 32(11): 3683-3691. [15] 梁胜杰, 张志华, 崔立林. 主成分分析法和核主成分分析法在机械噪声数据降维中的应用比较[J]. 中国机械工程, 2011, 22(1): 80-83. LIANG Shengjie, ZHANG Zhihua, CUI Lilin. Comparison between PCA and KPCA Method in Dimensional Reduction of Mechanical Noise Data[J]. China Mechanical Engineering, 2011, 22(1): 80-83. [16] 赵京, 李立明, 尚红,等. 基于主成分分析法的机械臂运动灵活性性能综合评价[J]. 机械工程学报, 2014, 50(13): 9-15. ZHAO Jing, LI Liming, SHANG Hong, et al. Comprehensive Evaluation of Robotic Global Kinematic Dexterity Performance Based on Principal Component Analysis[J]. Journal of Mechanical Engineering, 2014, 50(13): 9-15. [17] 赵京, 李立明. 基于主成分分析法和核主成分分析法的机器人全域性能综合评价[J]. 北京工业大学学报, 2014, 40(12): 1763-1769. ZHAO Jing, LI Liming. Comprehensive Evaluation of Robotic Global Performance Based on Principal Component Analysis and Kernel Principal Component Analysis[J]. Journal of Beijing University of Technology, 2014, 40(12): 1763-1769. [18] 孙志娟, 赵京, 赵辛. PCA与KPCA在并联机构综合性能评价中的应用比较[J]. 制造业自动化, 2014, 36(2): 66-71. SUN Zhijuan, ZHAO Jing, ZHAO Xin. Comparision between PCA and KPCA Method in Comprehensive Performance Evaluation of Parallel Mechanism[J]. Manufacturing Automation, 2014, 36(2): 66-71. [19] 王文博, 陈秀芝. 多指标综合评价中主成分分析和因子分析方法的比较[J]. 统计与信息论坛, 2006, 21(5): 19-22. WANG Wenbo, CHEN Xiuzhi. Comparison of Principal Component Analysis with Factor Analysis in Comprehensive Multi-indicators Scoring[J]. Statistics and Information Forum. 2006, 21(5): 19-22. [20] 秦寿康. 综合评价原理与应用[M]. 北京:电子工业出版社, 2003:135-142. QIN Shoukang. The Theory and Application of Comprehensive Assessment[M]. Beijing: Publishing House of Electronics Industry, 2003:135-142. [21] 林海明, 杜子芳. 主成分分析综合评价应该注意的问题[J]. 统计研究, 2013, 30(8): 25-31. LIN Haiming, DU Zifang. Some Problem in Comprehensive Evaluation in the Principal Component Analysis[J]. Statistical Research, 2013, 30(8): 25-31. ParameterOptimizationofParallelMechanismsBasedonPCA ZENG Daxing WANG Juanjuan FAN Mingzhou YUE Xiaobo HOU Yulei School of Mechanical Engineering,Yanshan University,Qinhuangdao,Hebei,066004 A DELTA parallel mechanism was treated as the research object, the global conditioning index, the global isotropic and the global minimum singular value of the mechanism were solved to build multi-dimensional global performance indices. Based on PCA, the multi-dimensional global performance indices were dimensionally reduced, effectively integrated. Redundant data dimensions among kinematic indicators and target function dependence of weight coefficient were reduced to obtain more objective target function. The different structure parameter samples were analyzed by PCA thereby optimal structure dimensions were obtained based on the comprehensive global performance. The optimization results of PCA and the distribution of the performance index values were compared and analyzed, the best and the worst samples corresponded to the best and the worst performance areas of distribution map of every global performance index respectively, and then the effectiveness of applying PCA in parameter optimization of parallel mechanisms was verified. These contents of the research provide a new idea for multi-target optimization of the parallel mechanisms. parameter optimization; parallel mechanism; principal component analysis(PCA); global performance index 2016-08-11 国家自然科学基金资助项目(51205339,51775473);河北省高等学校科学技术研究青年基金资助项目(QN2014175);河北省重点研发计划资助项目(15211826);燕山大学研究生创新资助项目(2017XJSS009) TH112 10.3969/j.issn.1004-132X.2017.24.001 (编辑苏卫国) 曾达幸,男,1978年生。燕山大学机械工程学院教授。主要研究方向为并联机构型综合、 并联机器人和重型工程机械设计。王娟娟,女,1991年生。燕山大学机械工程学院硕士研究生。樊明洲,男,1992年生。燕山大学机械工程学院硕士研究生。岳晓博,女,1990年生。燕山大学机械工程学院硕士研究生。侯雨雷(通信作者),男,1980年生。燕山大学机械工程学院教授、博士研究生导师。E-mail:ylhou@ysu.edu.cn。2.2 性能指标数据处理

2.3 求取相关系数矩阵

2.4 主成分的确定

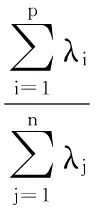
2.5 综合性能评价函数确定
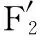
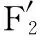
3 评价结果分析与验证



4 结论
