考虑土-结构相互作用的某高层结构地震动力分析

卢佳盛，李 勇，孙宝印

（1.厦门大学建筑与土木工程学院，福建 厦门 361005;2.阿尔伯塔大学土木与环境系，加拿大 阿尔伯塔，Edmonton T6E1A4；3.大连理工大学建设工程学部，辽宁，大连 116024）

考虑土-结构相互作用的某高层结构地震动力分析

卢佳盛1，李 勇2，孙宝印3

（1.厦门大学建筑与土木工程学院，福建 厦门 361005;2.阿尔伯塔大学土木与环境系，加拿大 阿尔伯塔，Edmonton T6E1A4；3.大连理工大学建设工程学部，辽宁，大连 116024）

土－结构体系有限元模拟计算分析的复杂性与计算成本，在一定程度上限制了土与结构相互作用分析在高层建筑结构设计中的应用。上部结构数值解与土解析解耦合的土－结构相互作用计算方法，为高层建筑结构提供了有效途径。利用作者提出的耦合算法，对一个钢框架-混凝土核心筒高层结构进行地震作用下的非线性动力分析,讨论了不同强度地震和不同种类地基土对结构地震反应的影响，得出了对实际工程具有指导性意义的结论。

高层结构；土-结构相互作用；耦合算法；地震作用；非线性动力分析

传统的结构工程设计与计算分析中，当楼层数不多、重量不大，且坐落于较硬地基时，结构与地基基础设计可采用刚性地基假设，因而忽略了土与结构相互作用（SSI）在地震动力分析中的影响。随着社会经济的发展，越来越多高层和超高层建筑结构的出现，特别是针对地基土的复杂情况，SSI效应必须考虑。核电站、高速铁路、大型桥梁工程的应用和理论研究表明[1-2]，上部结构在地震荷载下的动力反应，不仅取决于结构动力特性和自由场地震动输入动力特性的影响，还取决于土与结构在地震动过程中复杂的相互作用。这种相互作用主要包括惯性力影响（inertial effects）和运动作用影响（kinematic effects）[3]。因而近几十年来，学者们对建筑结构地震动力分析中的SSI进行了广泛的研究[4-5]。

地震动通过基础引起上部结构的变形，而上部结构的响应通过基础反过来影响地基的运动，形成SSI体系。在这样一个复杂体系当中，任何一个子结构（包括地基土、基础、上部结构）的动力响应都不是独立的。传统的计算方法包括不考虑地基土的变形（如中国建筑抗震规范，采用刚性地基假设）；或采用有限元[6]或有限元和边界元耦合[7]的方法分析整个上部结构和地基土，这种方法需要对地基土划分大量网格，计算成本巨大。本文对计算精度和计算时间作权衡，下部结构（地基土和刚性基础）采用解析解，无需对地基土划分网格，可以节省大量计算时间；上部结构采用有限元解，可以反映结构的非线性特征。本文通过分析高层建筑在SSI体系中受地震荷载的响应，考虑不同种类地基土的工况，与抗震设计规范的刚性地基假定计算结果作对比，说明考虑结构和土的相互作用在高层建筑结构的重要性，对实际工程的设计和计算有一定的指导意义。

1 SSI耦合算法

其中ug为地基土自由场的输入位移；us为SSI效应引起刚性基础与地基土的相对位移，由公式（2）得到。

其中，C（ω）为柔度矩阵，是关于频率ω的函数；Fs为刚性基础对地基土的合力。20世纪八九十年代，许多学者推导了各种形状的刚性基础在不同地基土条件下的动力刚度。考虑算法的实用性，本文采用假设刚性的矩形基础和线弹性地基土推导得到的动力刚度[9]，以及如图1所示的非迭代耦合算法，计算考虑SSI效应的高层结构响应。

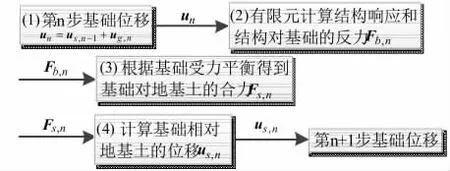
图1 SSI非迭代耦合算法

算法解释如下：

（1）计算第n步基础的位移向量un=us,n-1+ug,n；

（2）将un作为结构底部的地震激励，输入到有限元模型计算上部结构的响应，得到上部结构对基础的合力Fb,n（包括水平剪力和弯矩）；

（3）由Fb,n计算得到基础对地基土的合力Fs,n；

（4）由Fs,n通过时域离散递归法计算得到基础相对地基土的位移us,n，将在第2节详细介绍。

反复执行（1）～（4）步得到结构在地震荷载作用下每一时步的响应。

第（2）步求解结构响应时，有限元模型(FEM)无法作为主程序，但又需要被多次调用、连续计算。为避免从内存中释放和重新加载FEM程序，将FEM程序OpenSees作为一个常驻内存的服务器，将其他软件作为一个客户端（client）执行（1）、（3）、（4）步。客户端和服务端之间的通讯和数据传递采用Client-Server(CS)技术[10]实现，如图 2所示。

根据作者提出的算法[8]，刚性基础的位移为：

立体竹编编织的产品形状均为立体图形，主要有3大工序：起底、编织和锁口。首先根据产品的大小设计出相应的模具，再按照模具进行编织；起底即编织产品底部，以一定数量的粗细相近的竹篾作为骨干，相交编织成圆形，然后再编织不同的底面；编织筒身主要以经纬编织法为主，在此基础上穿插不同的技法，丰富编织的图案；锁口是在边缘处固定厚竹篾进行缠绕固定，对开口处进行加厚处理，锁口之前需将模具提前取出[3]。

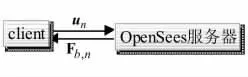
图2 基于CS技术的数据传递方式

第（3）步，由于基础相对上部结构质量很小，基础受到的惯性力可以忽略，因此假设上部结构对基础的Fb,n合力，与基础受到地基土的Fs,n合力大小相等，方向相反。

2 基础动力刚度由频域转为时域

介绍耦合算法的第（4）步，即由基础对地基土的合力Fs,n计算基础相对地基土的位移us,n。

本文利用文献[9]计算得到的柔度矩阵C(ω)，考虑二维情况下刚性基础的水平位移和转动。参考Safak[11]提出的动力刚度频域解转化为时域解的离散递归方法，将时域的解析解用于地震激励下高层建筑的时程分析。

时域离散递归方法，认为一个线性时不变系统系统的输入和输出呈线性关系，即

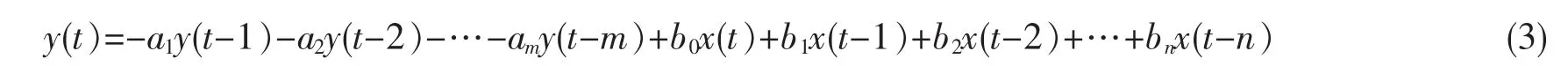
其中，y(t）是当前计算时步的输出项，y(t-1）、y(t-2）、…、y(t-m）分别是前一步、前两步、…前 m 步的输出项；x(t）是当前计算时步的输入项，x(t-1）、x(t-2）、…、x(t-n）分别是前一步、前两步、…前 n 步的输入项；a1、a2、…、am和 b0、b1、b2…、bn分别是常系数。

对于本论文设计的算法，由于基础假设为刚性基础，考虑平面内的刚体位移和外力，故时域离散递归公式应为：

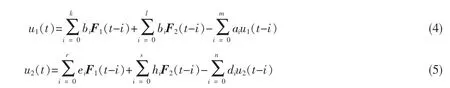
其中，u1（t）和 u2（t）分别表示刚性基础的水平位移和转动位移，F1（t）和 F2（t）分别表示刚性基础的水平合力和弯矩；a1、a2、…、am，b0、b1、b2…、bn，c0、c1、…、bl，e0、e1、…、er，h0、h1、…、hs。

利用 Fourier变换（6）及其时移性（7），

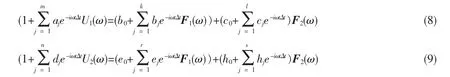
将公式（8）、（9）整理为矩阵的形式，得到

其中U1和U2分别是频域下刚性基础的水平位移和转角位移，F1和F2分别是频域下刚性基础的水平合力和弯矩；H1、H2、H3、H4分别是频域下刚性基础的柔度矩阵系数，表达式如公式11所示。

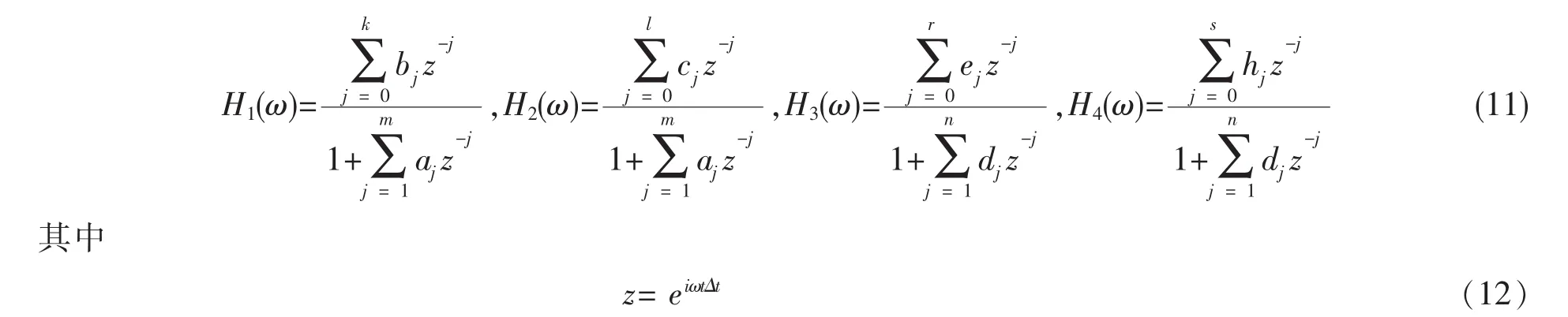
通过构造误差函数 V（公式 13），用最小二乘法（公式 14）求得柔度系数 H1(ω)、H2(ω)、H3(ω)、H4(ω)中的 a、b、c、d、e、h、等常系数，使得误差函数 V最小，从而与解析解的柔度矩阵 C(ω)拟合。 本文是采用MATLAB中的信号处理命令OE求解得到这些常系数。

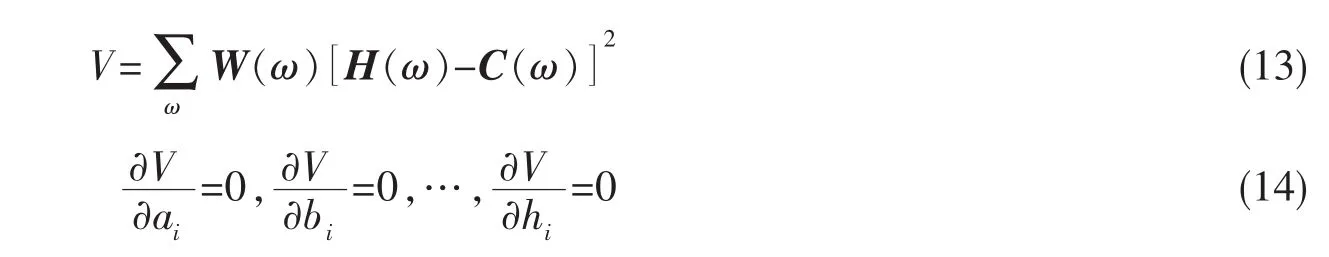
3 32层高层结构地震动力分析

3.1 高层结构模型介绍

该模型来源于中日弹塑性时程分析研讨会[12]，他们注重上部结构的建模分析，比较不同设计院的建模和计算结果，按抗震规范直接输入地震激励进行动力响应分析，没有提供具体的基础形式和地基土工况。本文出于对比考虑和不考虑SSI的区别，以及探究地基土如何影响结构的动力响应，结合高层建筑对基础形式的要求，以及现有的数据资料（矩形基础动力刚度解析解），基础简化为箱型基础，形状大致可以反映实际情况。结构典型平面布置和立面如图3所示，为钢框架-混凝土核心筒结构。结构层高32层，除底层5 m，其他均为4 m。平面投影为48 m×48 m。结构用OpenSees计算，模型共有1 980个节点，5 800个梁柱单元，896个剪力墙单元。其中，梁柱单元采用纤维截面模拟，混凝土选用concrete02，钢筋采用steel02；剪力墙采用分层壳单元[13]模拟。利用研讨会提供的Taft地震波（1952年）加载。按照设计资料和《建筑抗震设计规范》[14]，将地震加速度峰值（PGA）取为0.07 g（8度多遇地震）和0.4 g（8度罕遇地震）两种地震强度，地震持续时间取为15 s。

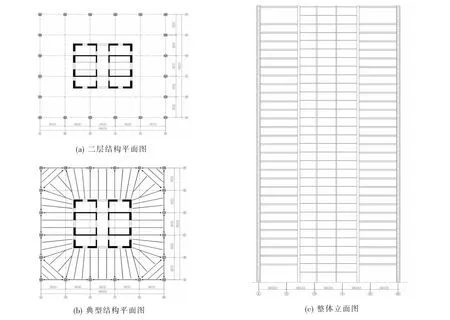
图3 型钢框架-混凝土核心筒结构典型平面布置和立面图

实际算法的实现，即第（4）步采用的是柔度矩阵，因此本文对动力刚度求逆，得到柔度系数，并对其进行拟合。由于柔度系数是复数，对其幅值和相位角都进行拟合，如图4所示。可以看到，拟合结果和文献中的解析解基本吻合。拟合结果与解析解对比，幅值的最大误差分别为1.94%、4.58%、4.58%、1.57%，相位角的最大误差分别为1.67%、5.88%、5.88%、3.46%。

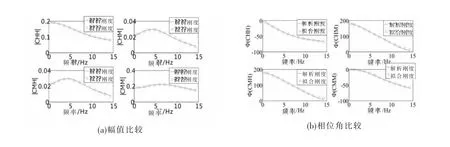
图4 拟合柔度系数和解析解柔度系数的比较

3.2 结果分析

分别计算了高层结构受两种强度地震激励下，在3种剪切波速的地基土（软弱土、中软土、中硬土）下的响应。

3.2.1 多遇地震下高层结构的响应（PGA=0.07g）

层间位移角包络线如图5所示。可以看到，4种工况下（即刚性地基、中硬地基土、中软地基土、软弱地基土工况）各层间位移角的最大值都出现在25层，其值分别为0.061%、0.060%、0.058%、0.052%。该高层建筑在第2层楼板处无横梁及其他斜向支撑，在第32层楼板处无其他斜向支撑，因此包络线在在第2、31层有突变，即此处层间位移角较上下楼层的大。随着地基土从刚性过渡到软弱地基，包络线逐渐往左移，因此各楼层的层间位移角峰值在逐渐减小。

楼层位移（相对基础）包络线如图6所示。刚性地基（可看做坚硬的岩石地基）假设计算所得的包络线和中硬土工况计算所得的包络线很接近（最大差别为0.9 mm），说明该算法的合理性。中软土的各个楼层位移峰值比刚性地基假设的大，软弱土的各个楼层位移峰值比刚性地基假设的小。顶部位移峰值，刚性地基假设、中硬土、中软土、软弱土工况分别为43、43、47、38 mm。说明多遇地震作用下，地基土类型对楼层侧移的影响有利有弊，应当具体计算讨论，没有统一的趋势。

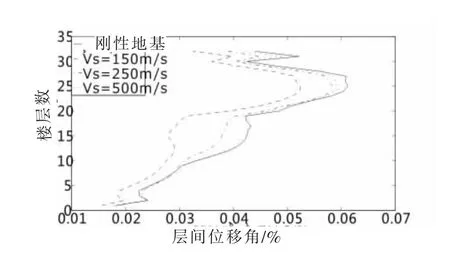
图5 层间位移角包络线(PGA=0.07g)

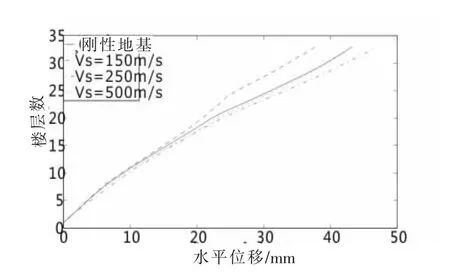
图6 楼层位移包络线(PGA=0.07g)

顶部加速度时程如图7所示（由于加速度曲线振荡剧烈，一张图难以显示清楚，因此取加速度较大的3～15s分两段显示）。整体趋势为：地基土越软弱，结构的顶部加速度越小。刚性地基假设、中硬土、中软土、软弱土计算得到的顶部加速度峰值，分别是2.4、2.2、2.0、1.8 m/s2。说明多遇地震作用下，越软弱的地基土，整体上越有利于减小结构的顶部加速度。

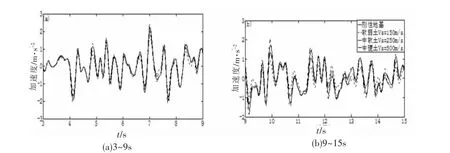
图7 顶部加速度时程(PGA=0.07g)

顶部位移（相对基础）时程如图8所示。整体趋势为：软弱土工况的顶部位移比刚性地基结果小最大差别为44 mm；中软土工况比刚性地基结果大，最大差别为25 mm；中硬土工况和刚性地基（可看做坚硬的岩石地基）假设计算所得的顶部时程曲线很接近，最大差别为8mm，同样说明算法的合理性。

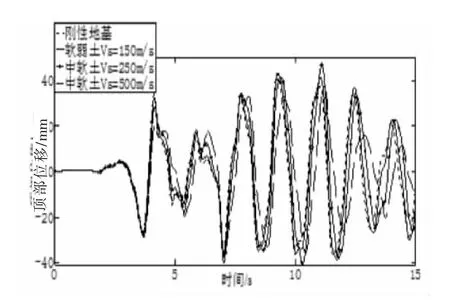
图8 顶部位移时程(PGA=0.07g)

各工况下某底部巨型柱的弯矩曲率关系如图9所示，该构件基本还未进入非线性。(a)、(b)、(c)、(d)分别对应刚性地基、中硬土、中软土、软弱土工况的弯矩曲率图。可以看到，地基土由硬到软，巨型柱的内力和变形逐渐减小，弯矩最大值分别为901.0、856.4、788.7、642.1kNm，曲率最大值分别为 1.10×10-4、1.06×10-4、9.91×10-5、7.01×10-5(1/m)。 说明越软弱的地基土，对减小底部柱构件的内力和变形越有利。

表1显示了各类地基土工况下对应的结构最大基底剪力。对比可以看到，地基土越软弱，最大基底剪力越小，说明多遇地震作用下，考虑SSI，结构的最大基底剪力有所减少。

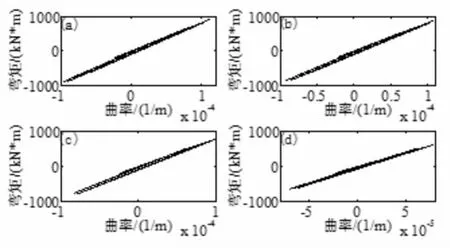
图9 各类地基土的结构底部巨型柱弯矩曲率图比较(PGA=0.07g)：

表1 各类地基土的结构最大基底剪力比较(PGA=0.07g)

3.2.2 罕遇地震下高层结构的响应（PGA=0.4g）

层间位移角包络线如图10所示。可以看到，四种工况下（即刚性地基、中硬地基土、中软地基土、软弱地基土工况）各层间位移角的最大值分别为0.30%、0.38%、0.41%、0.42%，分别出现在23、23、23、27层。随着地基土从刚性过渡到软弱地基，包络线逐渐往左移，说明各楼层的层间位移角峰值在逐渐减小。

楼层位移（相对基础）包络线如图11所示。刚性地基（可看做坚硬的岩石地基）假设计算所得的包络线和中硬土工况计算所得的包络线很接近（最大差别为4.8 mm），同样说明该算法的合理性。随着地基土从中硬土过渡到软弱土，包络线逐渐往左移，说明各楼层位移的峰值在逐渐减小。中硬土、中软土、软弱土工况的顶部位移峰值分别为310、302、248 mm。刚性地基假设计算得到的楼层位移包络线介于中硬土和中软土之间，可能是基于刚性地基假设计算楼层相对基础的位移时，不考虑基础转角位移对楼层侧移的影响。

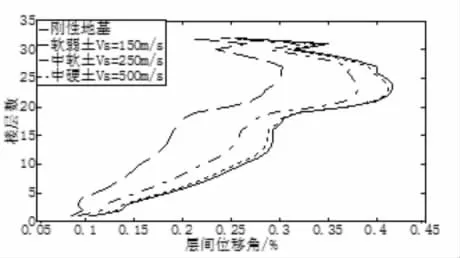
图10 层间位移角包络线(PGA=0.4g)

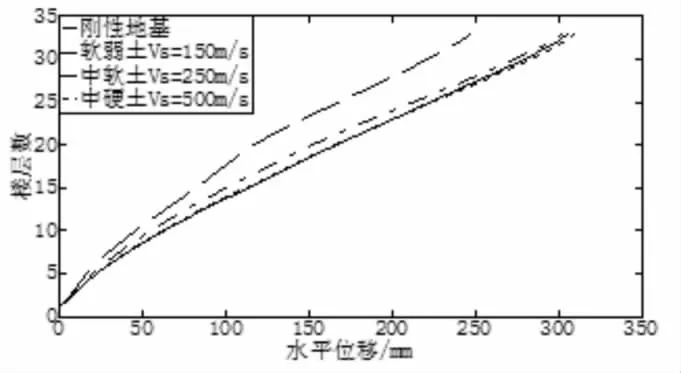
图11 楼层位移包络线(PGA=0.4g)

顶部加速度时程如图12所示。顶部加速度（由于加速度曲线振荡剧烈，一张图难以显示清楚，因此取加速度较大的3～15 s分两段显示）。整体趋势为：地基土越软弱，结构的顶部加速度越小。刚性地基假设、中硬土、中软土、软弱土计算得到的顶部加速度峰值，分别是11.9、11.3、10.7、9.6 m/s2。说明罕遇地震作用下，越软弱的地基土，整体上越有利于减小结构的顶部加速度。

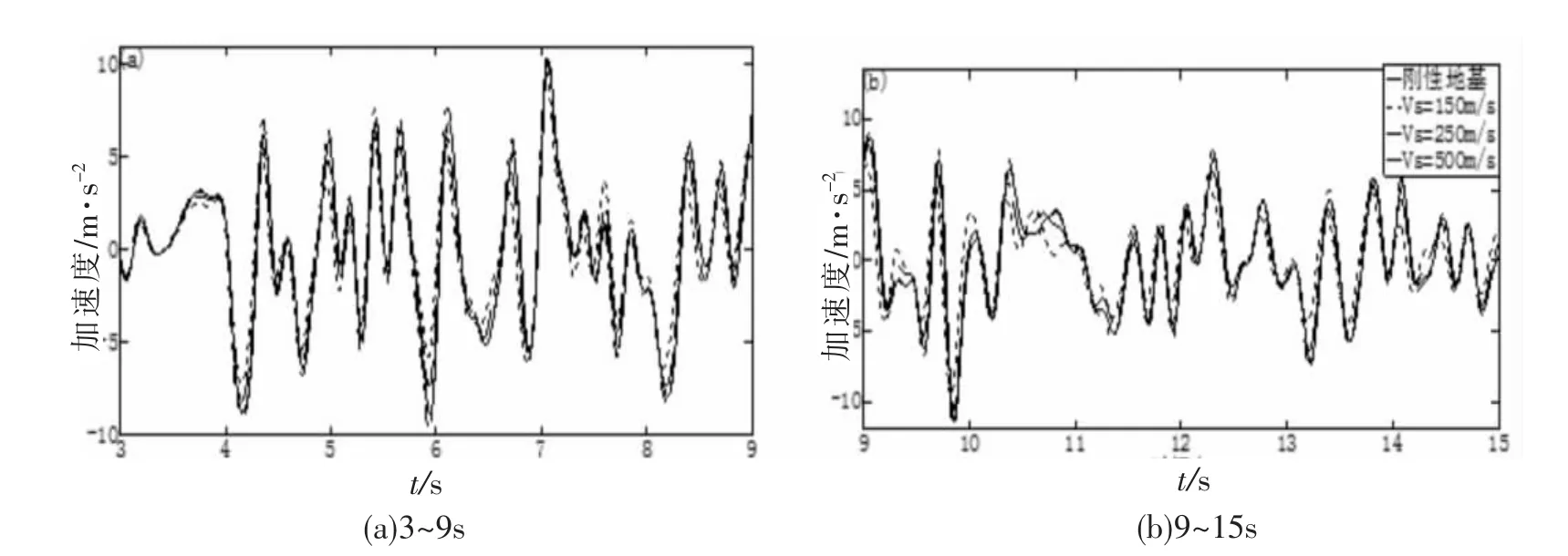
图12 顶部加速度时程(PGA=0.4g)

顶部位移（相对基础）时程如图13所示。可以看到，基于刚性地基假设计算得到的顶部位移时程曲线与中硬土、中软土工况很接近，而与软弱土相差较大，在结构整体振动过程中，刚性地基假设的顶部位移大于软弱土的，峰值相差58 mm。因此罕遇地震下，软弱地基土有利于减小结构的顶部位移。

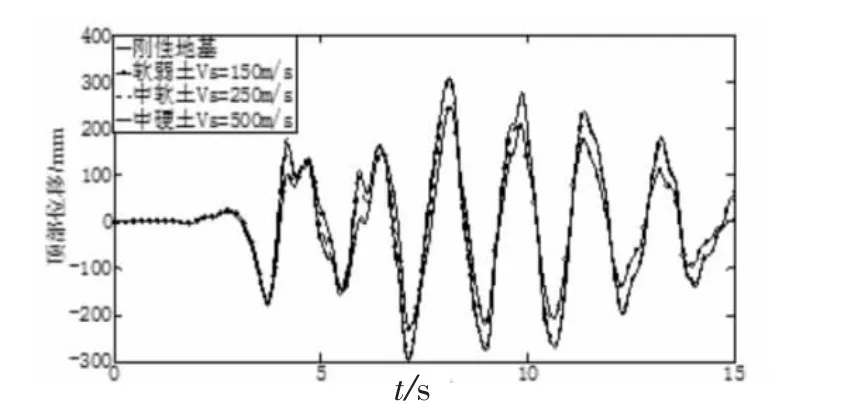
图13 顶部位移时程(PGA=0.4g)

表2显示了各类地基土工况下对应的结构最大基底剪力。对比可以看到，地基土越软弱，最大基底剪力越小，说明罕遇地震作用下，考虑SSI，结构的基底剪力有所减少。

表2 各类地基土的结构最大基底剪力比较(PGA=0.4g)

图14反映了底部的巨型柱在各类地基土下的弯矩曲率图，(a)、(b)、(c)、(d)分别对应刚性地基、中硬土、中软土、软弱土工况。该构件在四种工况下已经进入非线性。可以看到，地基土由硬到软，该构件进入非线性程度在逐渐减小， 弯矩最大值分别为 5.29×103、5.10×103、4.32×103、3.33×103kN·m，曲率最大值分别为 8.73×10-4、8.29×10-4、6.61×10-4、4.54×10-4(1/m)。说明越软弱的地基土，对减小底部巨型柱的内力和变形越有利。

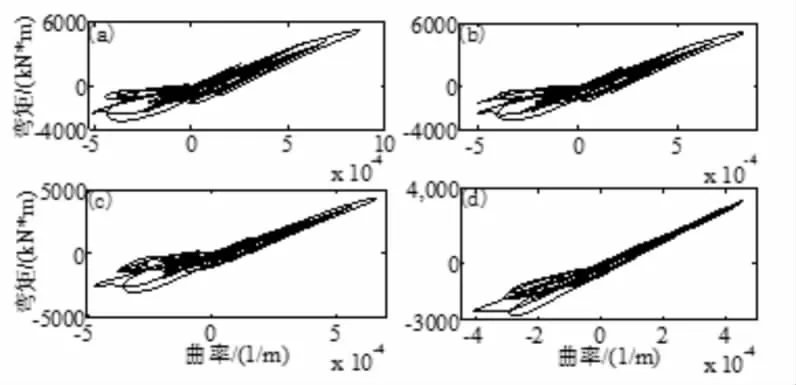
图14 各类地基土的结构底部巨型柱弯矩曲率图比较(PGA=0.4g)

4 结论

本文基于作者提出的考虑SSI的实用耦合计算方法，在多遇地震和罕遇地震作用下，考虑不同种类地基土工况，计算某32层高层建筑的动力响应，得到一些对实际工程有指导意义的结论。该高层结构受到地震激励，考虑SSI效应时某些响应会放大，另外一些响应会减小。具体结论如下：

（1）受多遇地震和罕遇地震激励，地基土越软，结构层间的位移角和顶部加速度均越小，基底剪力越小，底部柱构件的非线性程度减弱，内力和变形有所减小；

（2）多遇地震作用下，地基土类型对楼层侧移的影响有利有弊，没有统一趋势，例如在中软土地基上，顶部位移峰值较其他工况（中硬土、软弱土）的大；而罕遇地震下，地基土越软，各楼层位移峰值越小。

[1]CLOUTEAU D，BROC D，G．DEVE'SA，et al．Calculation methods of structure–soil–structure Interaction （3SI）for embedded buildings：Application to NUPEC tests[J]．Soil Dynamics and Earthquake Engineering，2012，32（1）：129–142．

[2]CHOUW N，HAO H．Significance of SSI and non－uniform near－fault ground motions in bridge response I：Effect on response with conventional expansion joint[J]．Engineering Structures，2008，30（1）：141–153．

[3]WOLF J P．土－结构动力相互作用[M]．吴世明，唐有职，陈龙珠 译.北京：地震出版社，1989．

[4]STEPHANE GRANGE，PANAGIOTIS KOTRONIS，JACKY MAZARS．A macro－element to simulate dynamic soil－structure interaction[J]．Engineering Structure，2009，31（12）：3034–3046．

[5]AMIR M KAYNIA．Dynamic stiffness and seismic response of pile groups[D]．Massachusetts Institute of Technology，1982．

[6]FARIBORZ NATEGHI A，ALI REZAEI－TABRIZI．Nonlinear dynamic response of tall buildings considering structure–soil–structure effects[J]．The Structural Design of Tall and Special BAuildings，2013，22（14）：1075–1082．

[7]RIZOS D C，WANG Z．Coupled BEM–FEM solutions for direct time domain soil–structure interaction analysis[J]．Engineering Analysis with Boundary Elements，2002，26（10）：877–888．

[8]HUANG SURONG，OZGUR OZCELIK，GU QUAN．A practical and efficient coupling method for large scale soilstructure－interac－tion problems[J]．Soil Dynamics and Earthquake Engineering，2015，76：44–57．

[9]AKIRA MITA，LUCO J E．Impedance function and input motions for embedded square foundations [J]．Geotechnical Engineering，1989，115（4）：491－503．

[10]GU QUAN，OZGUR OZCELIK．Integrating OpenSees with other software－with application to coupling problems in civil engineering[J]．Structural Engineering and Mechanics，2011，40（1）：85－103．

[11]ERDAL SAFAK．Time－domain representation of frequency－ dependent foundation impedance functions[J]．Soil Dynamics and Earthquake Engineering，2006，26（1）：65–70．

[12]何伟明，崔鸿超，程镇远．中日弹塑性时程分析实例计算比较汇总[J]．建筑结构，2013，43（16）：54－57．

[13]门俊，陆新征，宋二祥，等．分层壳模型在剪力墙结构计算中的应用[J]．防护工程，2006，8（3）：9－13．

[14]建筑抗震设计规范：GB50011－2010[S]．北京：中国建筑工业出版社，2010．

Dynamic Analysis of a High-rise-Building Structure during an Earthquake Considering Soil-Structure-Interaction

LU Jias-heng1,LI Yong2,SUN Bao-yin3
(1.School of Architecture and Civil Engineering,Xiamen University,Xiamen,Fujian 361005,China;2.Department of Civil and Environmental Engineering,University of Alberta,Edmonton,Alberta T6E1A4,Canada;3.Faculty of Infrastructure Engineering Dalian University of Technology,Dalian,Liaoning 116024,China.)

The conventional coupling analysis based on a comprehensive finite-element(FE)model is prohibitive in terms of computational complexity and cost.The coupling method between the numerical modeling of the superstructure and the analytical modeling of the soil provides an efficient approach for SSI.This paper applies this method to a steel-reinforced concrete frame-tube high-rise building and verifies its potential through this case study.Using this method,various soil conditions and earthquake intensities are studied to explore the SSI effects,leading to meaningful conclusions to engineering practice.

high-rise building;soil-structure-interaction;coupling method;earthquake excitation;nonlinear dynamic analysis

TU435

A

1673-4343（2017）06-0068-09

10．14098/j．cn35－1288/z．2017．06．011

2017-09-16

国家重点研发计划项目（2016YFC0701106）；国家自然科学基金项目（51261120376、5157847）

卢佳盛，男，广东汕头人，硕士研究生。主要研究方向：土和结构的相互作用。

朱联九）