多元线性回归模型应用实证分析
2017-12-28蔡素丽
蔡素丽
(福州外语外贸学院,福建福州 350018)
多元线性回归模型应用实证分析
蔡素丽
(福州外语外贸学院,福建福州 350018)
以福建省物流需求为研究对象,选取福建省1996-2015年货物吞吐量、全社会固定资产投资总额、农林牧渔总产值、进出口商品总额、居民消费水平、地区生产总值等统计数据,基于多元线性回归思路,诊断多重共线性。采用逐步回归法,以SPSS软件为工具,建立货物吞吐量与全社会固定资产投资总额以及进出口商品总额的二元线性回归模型。通过统计分析检验模型的有效性,运用货物吞吐量观测值与预测值的残差及相对误差检验模型的实践性。
多元线性回归;物流需求预测;逐步回归;多重共线性
1 多元线性回归模型概述
多元回归分析方法是多元统计分析方法中应用最为广泛的一种。它通过建立经济因变量与解释变量之间的回归模型,并对所建立的回归模型进行R检验,F检验,t检验,把符合判定条件的解释变量的数值代入回归模型,计算出经济变量的预测值[1]。
1.1 模型的选取
本文以多元回归分析方法研究福建省物流需求发展趋势,借助SPSS软件建立回归模型,采用最小二乘法原理进行模型估计与预测,以期为未来一段时间内物流基础设施建设、人才培养以及产业规划等提供一些数据支持。设Y为因变量,X1,X2,…,Xk为自变量,且Y与Xi(i=1,…,k)之间为线性关系,则多元线性回归模型为
1.2 模型的原理
最小二乘法是多元线性回归方程参数估计的最优方法,其原理为要求对每一组样本点X1,X2,…,Xk值,观察Yi值与回归值i的离差平方和最小。设Q(β0,β1,…,βk)表示离差平方和,则有
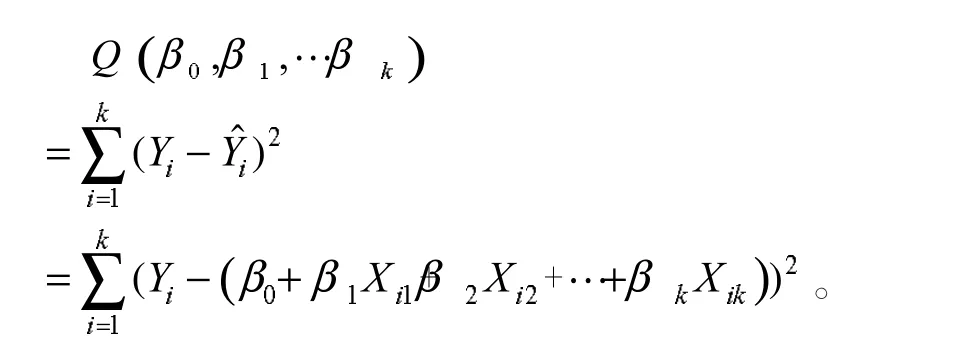
由多元微分学求极值原理,可得求解回归参数标准方程为:
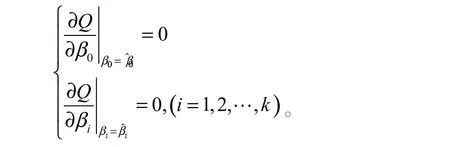
转换成矩阵形式:XTXβ^=XTY,求得β^=(XTX)-1XTY,其中

2实证分析——以福建省物流需求预测为例
2.1 模型指标的选取
物流需求是指一定时期内社会经济活动对生产、流通、消费领域的原材料、成品和半成品、商品以及废旧物品、废旧材料等的配置作用而产生的对物在空间、时间和费用方面的要求,涉及运输、库存、包装、装卸搬运、流通加工以及与之相关的信息需求等[2]。考虑到运输是现代物流体系的中心环节,以及获取数据的完整性、一致性和时效性等方面因素,本文选取1996-2015年福建省统计年鉴上的数据作为样本数据,选取物流货运量(万吨)为物流需求指标Y,选取全社会固定资产投资总额X1(亿元)、农林牧副渔总产值X2(亿元)、进出口商品总额X3(千万美元)、居民消费水平X4(元/人)、地区生产总值(亿元)X5等5个因素为物流需求预测的经济指标[3]。

表1 1996—2015福建省部分统计数据
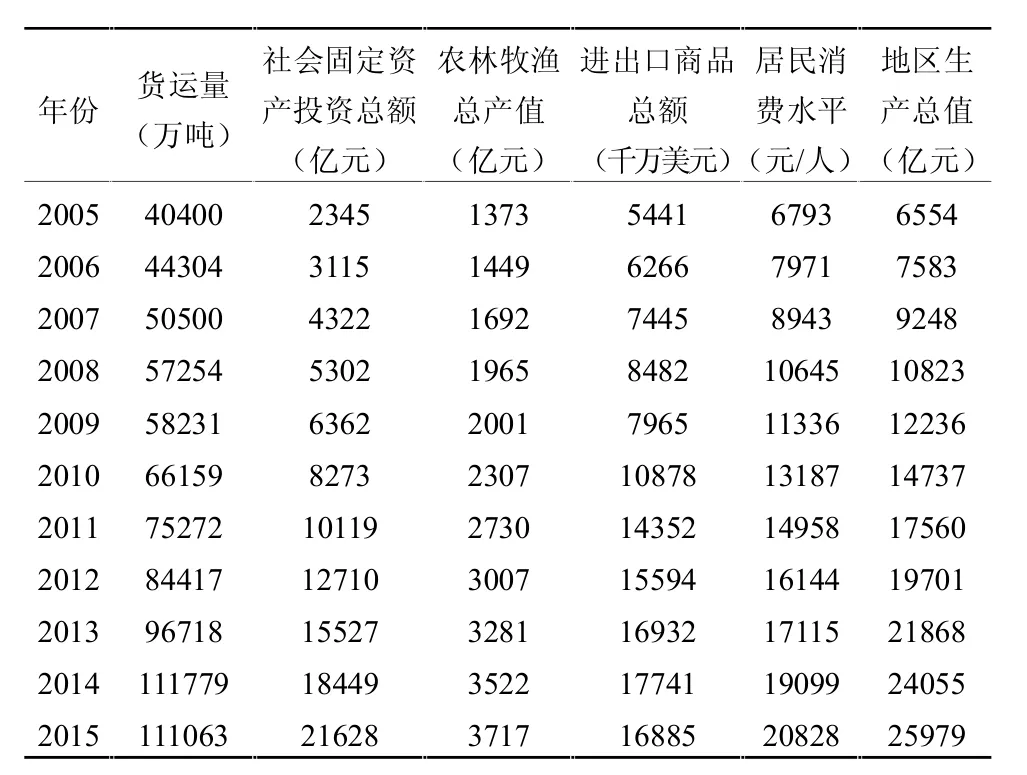
资料来源:根据《2016年福建统计年鉴》整理
2.2 多重共线性诊断
在多元线性回归模型中,自变量之间可能存在线性相关的关系,会使得系数估计的标准误差增大,从而使得模型的预测精度大大降低,称之为多重共线性。使用SPSS软件全回归法对所选取的指标建立模型,发现模型整体是显著(R2=0.996,F=620.284,Sig=0.000)的,但是对模型系数的检验表明很多变量对“货运量”的影响并不显著。由表2可知,t统计量与Sig值均不显著。自变量之间很可能存在共线性的问题。计算各解释变量的相关关系,表3数据表明各解释变量间存在严重的多重共线性。笔者改用多元逐步回归法对物流需求与各经济指标建立模型,减少多重共线性对模型参数估计、模型误差以及稳定性等的影响。
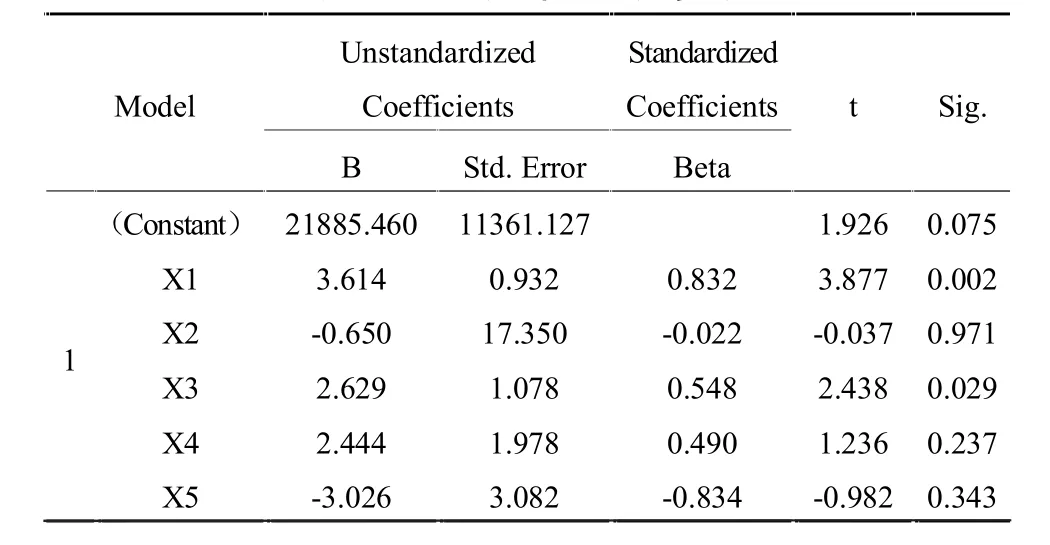
表2 全回归部分回归参数

表3 相关系数
2.3 多元逐步回归
多元逐步回归的基本思想是:对全部因子根据其对因变量Y影响程度的大小(即偏回归平方和R2值的大小),从大到小逐个地引入回归方程,同时对回归方程当时所含的全部变量进行统计检验,观察其是否仍然显著,如果不显著就将其移出模型,直到回归方程中所有的变量对因变量的Y作用都是显著的,再考虑引入新的变量。再在剩余的未选因子中,选出对因变量Y的作用最大者,检验其显著性,若显著则引入方程,若不显著则不引入,直到最后再也没有可以引入的显著因子,也没有不显著的变量需要移除为止。多元逐步回归分析本质上没有新的理论,只是在多元线性回归内部运用一些计算技巧获得最优的多元线性回归方程,是实用且被广泛应用的统计分析方法。
在逐步回归中,变量X2、X1、X3被逐个引入,在第三个模型中X2被移除,最终得到模型4。模型4解释变量为 X1、X3,模型整体显著(R2=0.994,F=1689.362,Sig=0.000),模型系数检验显著。tX1=10.573,SigX1=0.000;tX2=10.573,SigX2=0.000,DW=1.602,比较理想,模型可以认为不存在自相关性[5]。解释变量X1、X3的方差膨胀因子VIF=11.707比10略高,多重共性性仍然存在,可以考虑主成分回归或者岭回归,本文不再继续探讨。
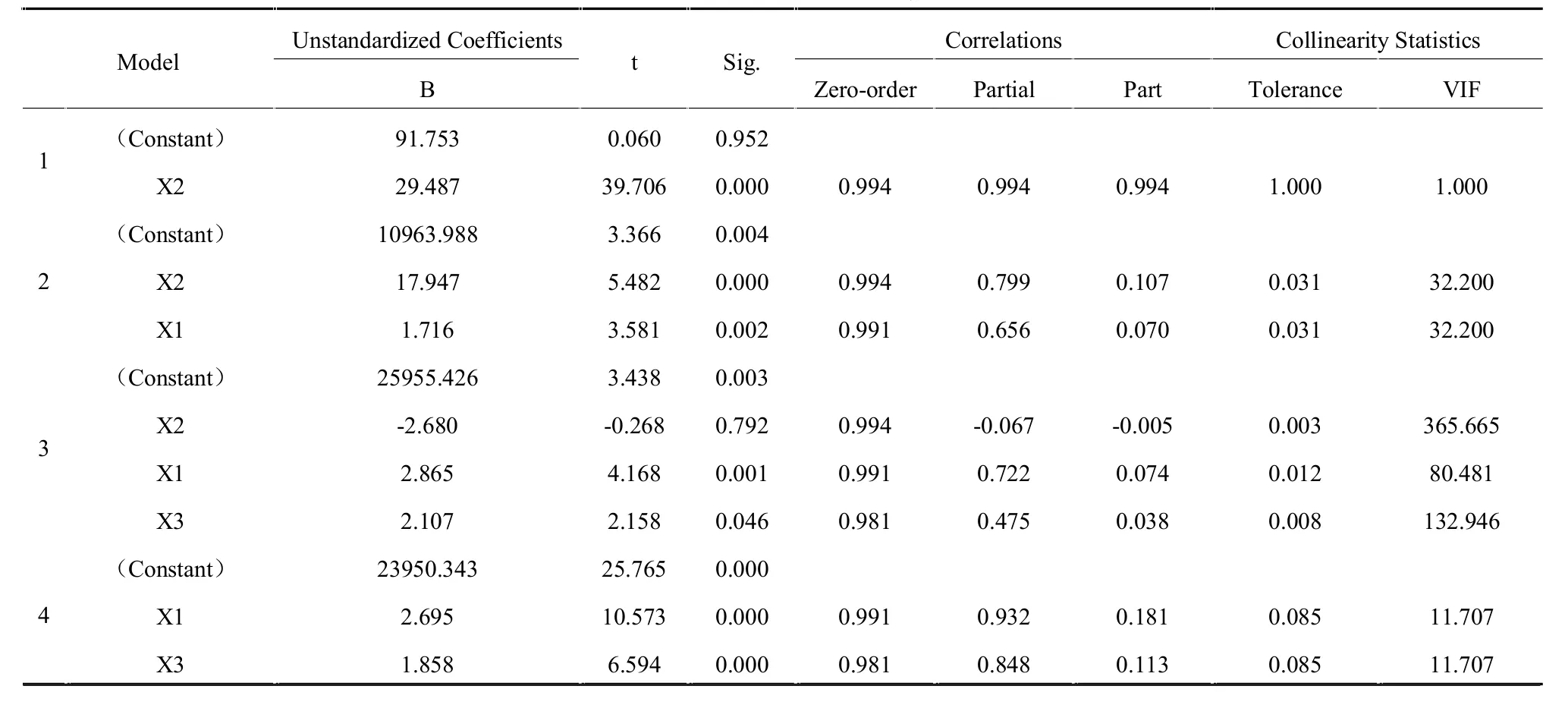
表4 逐步回归部分回归参数
2.4 物流需求预测模型
由表4模型4可得物流需求预测回归模型:Y=2.695X1+1.858X3+23950.343,其中X1为社会固定资产投资总额(亿元),X3为进出口商品总额(千万美元)。模型整体检验显著、模型系数检验显著,具有一定的分析价值。由该模型计算得出1997-2016年物流货运量预测值,由表5可知少数年份残差较大,但相对误差除2008年略高于5%,其他年份均在5%以下。标准化残差正态曲线直方图如图1所示,标准化残差概率图如图2所示。可以看出标准化残差呈正态分布,散点在直线上或下靠近直线,回归方程满足线性以及方差齐次的检验[6]。物流需求预测模型通过实践检验。
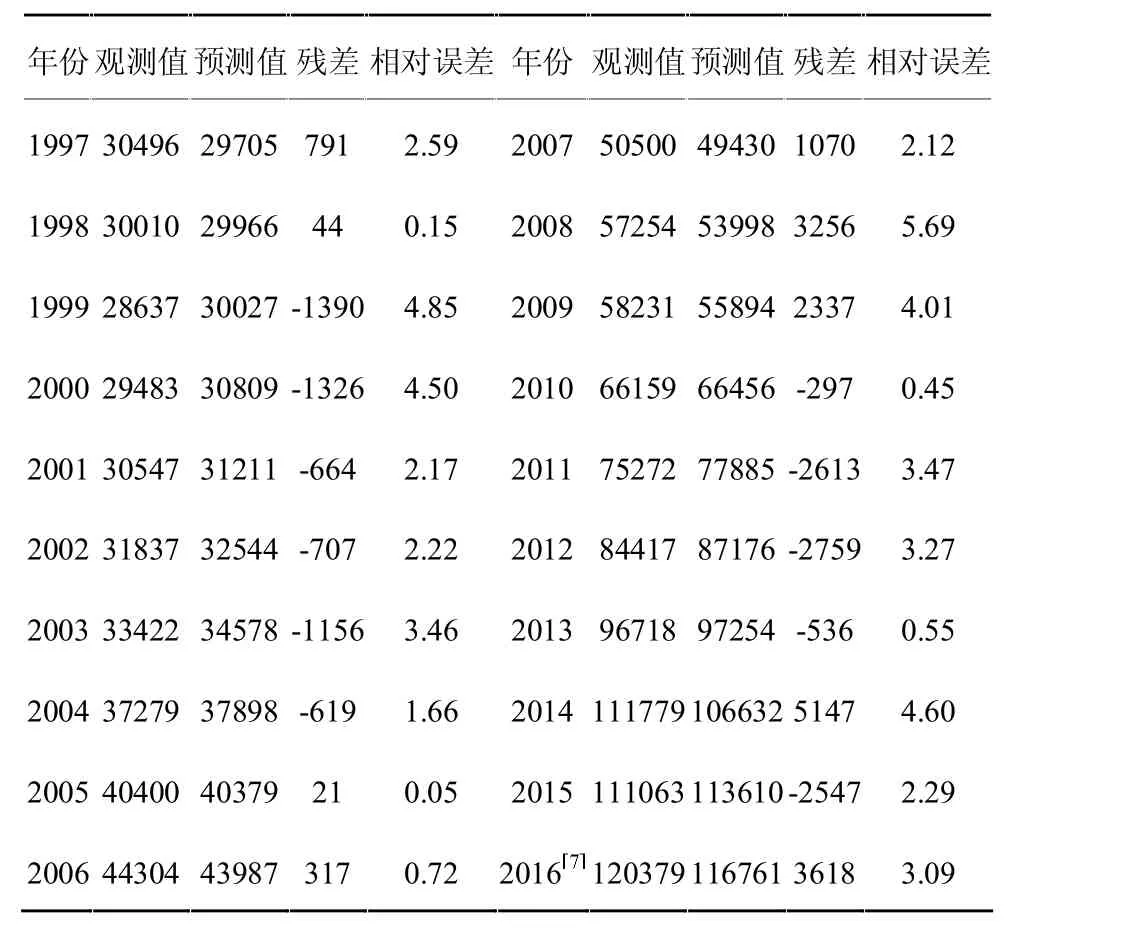
表5 1997-2016年物流需求回归预测值

图1 标准化残差直方图

图2 标准化残差正态P-P图
3 结论
基于1996-2015年福建省货运量及相关统计数据建立的多元线性回归模型,表明福建省货运量与全社会固定资产投资总额、进出口商品总额表现出高度的相关性。农林牧副渔总产值、居民消费水平、地区生产总值等经济指标与货运量也存在很强的相关关系,但由于各变量间存在较强的多重共线性,在逐步回归中被剔除。由偏边际经济理论可知,在进出口商品总额不变的情况下,全社会固定资产投资总额每增加1个单位,物流需求增长2.695个单位;在全社会固定资产投资总额不变的情况下,进出口商品总额每增加1个单位,物流需求增长1.858个单位。从模型可以看出,全社会固定资产投资对物流需求的影响较大。近年来,福建省在物流运输基础设施建设方面力度逐年加大,在全省各地已经建立或在建多个大型物流园区、港口、配送中心,大型物流企业蓬勃发展,物流产业转向信息化现代化。国有经济资产投资、城乡集体经济资产投资、各种经济类型的资产投资以及城乡居民个人投资等社会资产投资的增长都积极促进了物流产业的发展。
[1]蔡素丽.福州空港物流与经济发展关系模型研究[J].湖南城市学院学报(自然科学版),2015,24(4):58-60.
[2]刘华,孟建华.现代物流管理概论[M].北京:清华大学出版社,2010.
[3]赵洪丹,邹之坤.农村金融发展与农村经济增长关系的实证研究[J].廊坊师范学院学报(自然科学版),2010,10(6):79-81.
[4] 2016 福建统计年鉴 [EB/OL].http://www.stats-fj.gov.cn/tongjinianjian/dz2016/index-cn.htm,2016-08-30.
[5] 蔡素丽.灰色系统理论 GM(1,1)预测模型应用实证分析[J].廊坊师范学院学报(自然科学版),2015,15(6):5-8.
[6]时立文.SPSS19.0统计分析从入门到精通[M].北京:清华大学出版社,2015.
[7] 2016 福建统计公报 [EB/OL].http://www.stats-fj.gov.cn/xxgk/tjgb/201702/t20170224_40079.htm,2017-02-24.
Empirical Analysis of Multiple Linear Regression Models
CAI Su-li
(Fuzhou University of International Studies and Trade,Fuzhou 350018,China)
This paper takes the logistics demand of Fujian Province as the object of study,and chooses cargo throughput,total social fixed asset investment,total output values of agriculture,forestry,pasturage and fishery,total import and export commodities,household consumption level and regional GDP of Fujian province as the data indicator to diagnosing multiple commonalities based on the multiple linear regression.Using stepwise regression method and SPSS software to establish binary linear regression model of cargo throughput with the total value of total social fixed asset investment and total import and export commodities.The validity of the model is verified by statistical analysis.The residual and relative error of the cargo through put observation value and the predicted value is applied to test the practicality of the model.
multiple linear regression;forecast of logistics demand;gradual regression;multicollinearity
O212
A
1674-3229(2017)04-0005-04
2017-08-25
蔡素丽(1980-),女,硕士,福州外语外贸学院语数教学部副教授,研究方向:应用数学、数量经济学。
