伯努利方程在燃油供给系统中的应用

杨中华 ，李怀军 ，梁 涛 ，黄 松

（1.长城汽车股份有限公司技术中心，河北 保定071000；2.河北省汽车工程技术研究中心，河北 保定071000）

伯努利方程在燃油供给系统中的应用

杨中华1，2，李怀军1，2，梁 涛1，2，黄 松1，2

（1.长城汽车股份有限公司技术中心，河北 保定071000；2.河北省汽车工程技术研究中心，河北 保定071000）

本文通过对伯努利方程的介绍，引用该方程在汽车燃油供给系统的应用。重点介绍了喷油器和伯努利方程的对应关系，通过对实际燃油系统布置的介绍，说明伯努利方程在有或者无回油燃油系统中的实际应用情况和注意事项，并根据实际燃油系统参数进行了理论阐述和试验验证。

伯努利方程；喷油器；理想流体；有/无回油系统；燃油压力调节器

随着油耗及排放法规的日趋严格，发动机EMS系统对燃油的精确控制，是满足油耗和排放的前提。为保证精确控制，需要大量试验和校验。本文以伯努利方程为切入点，进而引用到车辆实际燃油供给系统中来，对PFI发动机喷油器工作原理和喷油量的理论计算进行了研究和分析，有助于加深燃油系统物理背景的理解，便于喷油量计算等实践应用。

图1 理想液体伯努利方程之一

1 伯努利方程[1]

如图1所示，在以截面积变化的弯曲管路中，稳定流动着充满整个管路的不可压缩的密度为ρ的理想流体。设Ⅰ处的压强为p1，截面积为A1；在Ⅱ处的压强为p2，截面积为A2.按照流体动能定理，有

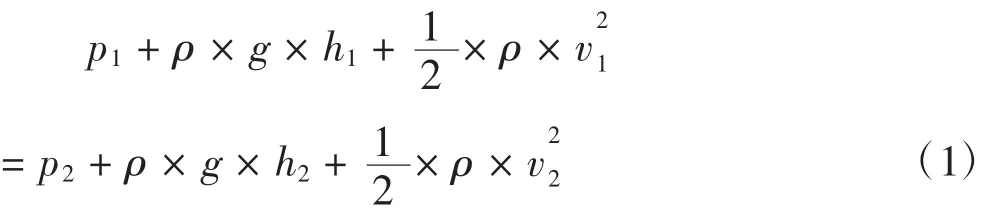
此即伯努利方程。它是能量守恒在流体力学中的一种表达式，显然也是牛顿力学基本原理在流体中的应用。

如图2所示，如果将流体管路放置在水平位置上，h1=h2，那么伯努利方程可以写成

图2 理想液体伯努利方程之二

2 燃油供给系统模型的建立

以PFI发动机的喷油器作为研究对象，如图3所示。

图3 喷器构造

在发动机燃油供给系统中，喷油器、燃油导轨以及供油管，一起构成了充满燃油的管路，现在把喷油器作为研究对象。设燃油为不可压缩的理想流体，密度为ρfuel，取喷油器上游压力为p1fuel，喷油器喷孔处压力为p2fuel.由于喷油器安装在进气道中，喷油器喷孔处的压力即为歧管压力pintake.管路容积很大，相对于喷孔处，管路中流体的速度v1fuel≈ 0，那么喷孔处流体的流速v2fuel可以用伯努利方程（5）表示

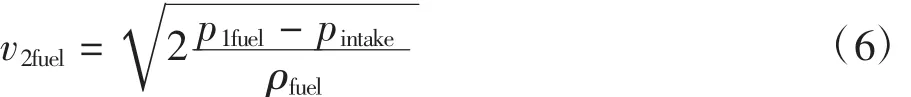
设喷孔的面积为A，根据一维定常流动方程，流过喷孔流体的质量流量m可表示为，

可见，喷油器的质量流量与其喷孔面积、喷孔前后的压力差和流体的密度相关。众所周知，流体的密度与其温度相关，温度一定则密度一定。设喷孔面积为常量，喷油器流量主要与燃油的温度和喷孔前后的压力差相关。由于温度引起的密度变化，相比于喷油前后压力差对喷油量的影响要小很多，为了便于分析，本文暂忽略温度影响，即燃油为理想流体，密度为定值ρ.

通常静态流量是表征喷油器流量特性的参数，它是在特定的测试状态下，通过专业测试设备直接获取的。测试过程通常恒定流体温度T、恒定的喷孔前后压力差△p，把这种测试状态定义为标准测量状态。理论上，只需要获取一组温度T和压力差△p下的静态流量就可以了。

已知某喷油器标准测量状态下温度T和压力差△p＝p1-p2，其静态流量为Qm.设其喷孔面积为A，密度为ρ，用一维定常流动方程[2]（8）可表示为：其中是燃油压力差变化对标准测试状态喷油量的修正，这正是伯努利方程在实际燃油系统中的应用。

已知喷油器的喷油脉宽为t，歧管的压力为pintake，环境压力为pair，燃油导轨压力为pfuel，发动机转速为N，缸数为i，冲程数为τ.那么，根据喷油器的静态流量就可以求得该转速下的喷油量m.即

这就是燃油系统供油量的通用计算公式。其中，m 为喷油器质量流量（kg/h）；t为喷油脉宽（ms）；Qm为静态流量（g/min）；N 为转速（r/min）；△p为标准测试状态压力差（kPa）；△p′为实际系统压力差（kPa）；τ为冲程数；i发动机缸数。

在实际的车辆状态中，其喷孔前后压力差△p′会根据实际燃油系统的布置有两种情况。

一种叫有回油燃油供给系统，布置示意图如图4所示。

图4 有回油燃油系统

喷油器安装在进气歧管上，燃油经过燃油滤进入油轨，油压为p1，作用在燃油压力调节器膜片一侧；歧管压力为p2作用在喷油器喷孔处，同时也作用在压力调节器膜片另一侧。压力调节器弹簧预紧力为F，压力调节器的膜片面积为A，以上参数在膜片上下构成力学平衡方程p1×A＝p2×A+F，所以p1-p2＝F/A，可见只要弹簧预紧力F一定，p1-p2＝F/A就为定值，所以可以通过调整弹簧预紧力F或膜片的面积A来达到稳定系统压力的目的。由此可见，在有回油系统中喷油器喷孔的前后压差p1-p2是定值，即△p是常数。如果，△p＝△p′，就无需进行压力修正，代入（13），即

另一种叫无回油燃油供给系统，布置示意图如图5所示。

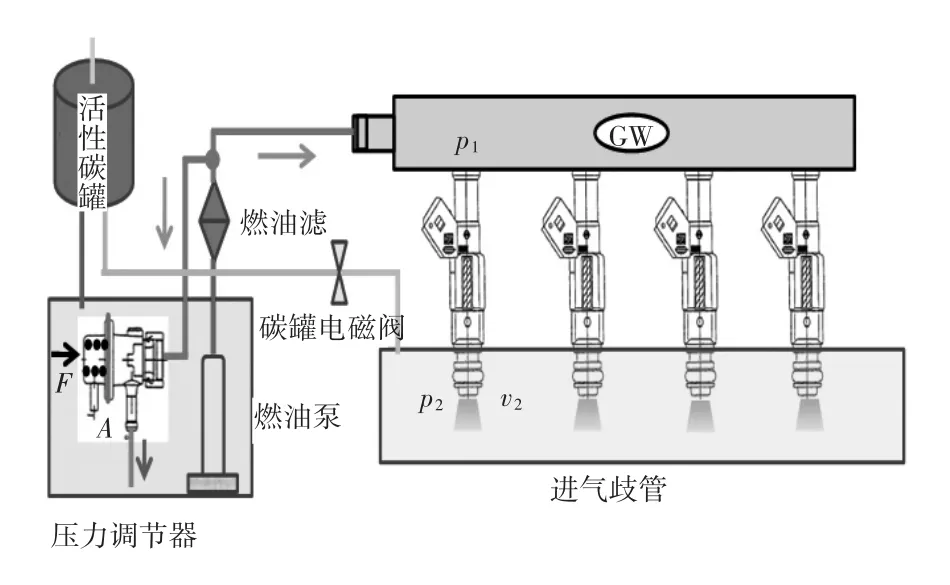
图5 有无油燃油系统

该系统与有回油系统的最大区别就是燃油压力调节器安装回路的改变。压力调节器布置在油箱中，特别要注意其压力调节的进油口是位于燃油滤清器之后，这样就可以保证即使是燃油滤芯出现脏堵而又较大压力损失的情况下也能保证油轨的压力为恒定值，除非燃油滤芯的压力损失已经使得滤芯后油压小于目标调节的压力。同理，根据系统中的力平衡方程有p1×A＝F，可见通过设计弹簧预紧力F的大小可以使燃油导轨的压力恒定。但对于喷油器，其两端的压力差△p′则是变化的。已知标准测试状态下的喷油器流量为Qm，对应的标准环境条件为△p和温度T；实际油轨状态下的流量为Q′m，其对应的条件为△p′，温度为 T′，忽略温度的影响设 T=T′，那么（13）式有，

考虑到有回油管路布置和回油对油箱加热、布置和成本等因素，当前市场上大多数系统都采用无回油系统。

3 模型结果的验证

以无回油燃油供给系统为例，验证以上的理论公式。已知其静态流量Qm=220 g/min，标准测试状态压力差△p=380 kPa，温度T=25℃.实际测试条件和计算结果如表1所示。

表1 实际测试条件和计算结果表

其中，油耗差为计算值与实际值的差，差比为计算值相对实测值相差的百分比。可见，根据伯努利方程进行简单的理论计算可以较为精确的估算喷油量，与实际喷油量的偏差在5%以内。要注意的是这里没有考虑管路的压降、油温、粘度和喷油器非线性区域等影响，所以试验过程中尽可能保持温度和压力的稳定性，同时要让喷油工作在其线性区域，这样的计算结果才更加准确[1-2]。

4 结束语

伯努利方程是一个理想的简化模型，一般的工程计算和建模可以满足要求，这种类喷嘴的模型均可以使用。对于更高精度的计算，需考虑流体的温度、粘度、压力脉动、流量系数、非线性区域等因素影响。

[1]李 莉，宋英杰，池翠薇.流体动力学方程的探讨[J].承德石油高等专科学校学报，2007，9（3）：37-39..

[2]肖 琼，颜伏伍，邹 华，等.电控喷油器流量特性试验台的开发与试验分析[J].中国机械工程，2005，16（16）：1419-1422.

The Application of Bernoulli Equationin the Fuel Supply System

YANG Zhong-hua1，2，LI Huai-jun1，2，LIANG Tao1，2，HUANG Song1，2
（1.Great Wall Motor Company Technical Center，Baoding Hebei 071000，China；2.Hebei province Automobile Engineering Technology Research Center，Baoding Hebei 071000，China）

In this paper，by introducing the bernoulli equation，the application of this equation in automotive fuel supply system is introduced.Focuse on the correspondence between injector and bernoulli equation in this paper，and via introducing the actual fuel supply system layout，narrate the practical application and the matters needing attention which according to the application of the bernoulli equation in the fuel supply system with/without returning fuel system.According to the actual fuel system parameters，theoretical explanation and experimental verification are introduced.

bernoulli equation；injector；ideal fluid；with/without returning fuel system；fuel pressure regulator

U464.9

A

1672-545X（2017）10-0132-04

2017-07-08

杨中华（1980-），男，河北宣化人，本科，工程师，研究方向：发动机控制策略、标定和燃烧开发，长城汽车；李怀军（1984-），男，内蒙古兴安盟突泉人，副高级工程师，学士，研究方向：内燃机燃烧和标定开发，国六项目开发；梁 涛（1986-），男，陕西汉中人，学士，工程师，研究方向：发动机研发；黄 松（1987-），男，河北保定人，硕士研究生，研究方向：发动机标定。