基于遗传算法优化小波神经网络的煤炭铁路运量预测模型研究
2017-12-27张正义王公强牛天河
张正义,王公强,牛天河
西安铁路职业技术学院,陕西西安710014
煤炭铁路运量预测能够有效调度铁路车辆和优化煤炭运输资源配置,更为铁路煤炭运输通道发展规划提供重要决策依据[1]。煤炭铁路运输受诸多因素影响,从经济走势看,当前我国供给侧改革进入“快车道”,煤炭的产量发生了较大的变化,同时煤炭的价格也出现了较大的波动,价格变动直接影响需求量,需求量的变化直接影响煤炭运输活动。综合相关的调研数据并结合文献资料,可将影响煤炭铁路运输的关联影响归纳为以下9个基本要素,包括煤炭平均价格、煤炭铁路运输费用、煤炭公路运输费用、煤炭水路运输费用、煤炭消费量、工业总产值、铁路通车里程、煤炭产量、铁路运煤专线里程,内容如表1所示。

表1 煤炭铁路运输相关影响因素Table 1 Factors related to coal railway transportation
1 模型建立
本文以嵌入式小波神经网络作为炭煤铁路运量预测模型构建的基础,此种建模方法能够充分利用小波变换的优势特征,保证模型具备较强的逼近与容错能力[2]。但影响煤炭铁路运量的因素具有较强的复杂性和随机性及不确定性,小波神经网络会容易引起振荡效应和陷入局部极小[3]。为了有效的改进这一问题,需要将具有自然进化规律的遗传算法引入小波神经网络[4]。本文建立的预测模型以遗传算法来克服小波神经网络的前期搜索不足,并集合遗传算法的全局搜索寻优和BP网络局部搜索寻优,保证预测结果精确。优化模型首先进行小波神经网络的参数确定,然后以优化后的参数进行小波神经网络计算,直至得到最优解[5]。模型建立步骤如图1所示。
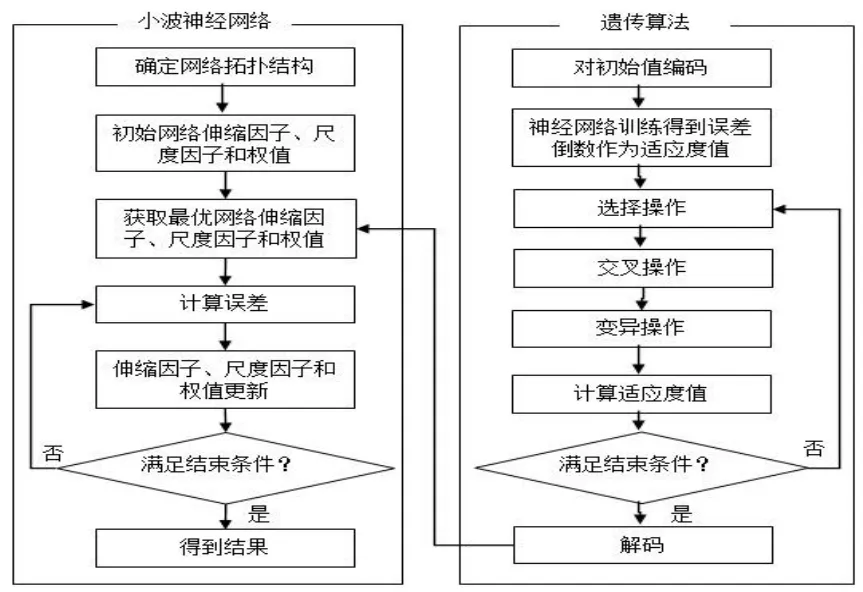
图1 基于遗传算法的小波神经网络煤炭铁路运量预测模型Fig.1Forecast model of coal railway transportation volume based on wavelet neural network optimized by genetic algorithm
2 模型求解
依据建立的模型设定MATLAB求解,求解关键程序示例如下:
(1)数据归一化程序示例

[XX,minp,maxp,YY,mint,maxt]=premnmx (XX,YY);
(2)遗传算法优化程序示例

P=XX;%输入变量T=YY;%输出变量…………………….plot(trace(:,1),1./trace(:,3),'r-');xlabel('Generation');ylabel('Fittness');
(3)小波神经网络训练程序示例

[W1,B1,W2,B2,P,T,A1,A2,SE,val,V]=gadecod(x);…………………….xlabel('样本序号');ylabel('煤炭铁路运量');end
(4)适应度函数程序示例

function[sol,val]=gabpEval(sol,options)…………………….end;[W1,B1,W2,B2,P,T,A1,A2,SE,val]=gadecod(x);end
(5)编解码和隐含层函数程序示例

function[W1,B1,W2,B2,P,T,A1,A2,SE,val,V]=gadecod(x)……………………end B2(i,1)=x((R*S1+S1*S2+S1)+i);sum=sum+abs(T(i)*log(A2(i))+(1-T(i))*log(1-A2(i)));
3 实例验证
由前文确定的影响因素可知,在进行模型求解时输入和输出的变量如表2所示。

表2 煤炭铁路运量预测模型输入输出变量Table 2 Input and output variables of coal railway traffic volume prediction model
为了获取尽可能多的样本数据进行小波神经网络的学习和训练,选取了表1中1986~2015年的数据进行训练和测试。
计算中持续对参数进行修正训练,显示其初始种群数为30时,MATLAB计算所得的遗传算法误差曲线如图2所示,适应度函数值变化曲线如图3所示。由图2和3横坐标可知,适应度函数值和误差(嫡)函数趋于稳定在算法进行了100代之后就不再发生变化。因此,将最大进化代数100作为算法的结束条件。表3所示为测试样本预测值和实际值之间的差异,样本的预测值与实际值对比如图4所示。

图2 预测模型的误差(熵)函数曲线Fig.2 The error(entropy)function curve of predictive model

图3 预测模型的适应度值曲线Fig.3 The fitness value curve of predictive model

表3 煤炭铁路运量测试样本误差值Table 3 The test sample differences of coal railway traffic
从预测结果看:在选定的测试样本中,其预测值和实际值之间的相对误差均不高于3%,由此可知本文构建的煤炭铁路运量预测优化模型具有较高精度,能反映煤炭铁路运量的形成机理。
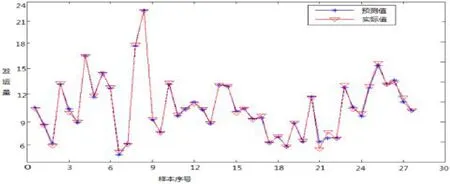
图4 模型的实际运量和预测值Fig.4 Actual volume and forecast value of the model
4 结论
(1)综合相关资料数据,最终确定了影响煤炭铁路运输量的关联因素,选取其中9个核心要素煤炭平均价格、铁路煤炭运输费用、公路煤炭运输费用、水路煤炭运输费用、煤炭消费量、工业总产值、铁路通车里程、煤炭产量、现有铁路运煤专线里程进行关联;
(2)由建立的优化模型计算得到的最终结果可知,算法得到的运量预测值与实际值的相对误差均不高于3%,由此可以验证模型精度较高,同时表明选取的影响因素具有很高的关联性。
[1]张翠云.基于灰色马尔可夫链的铁路煤炭运量预测研究[J].煤炭经济研究,2007(12):41-43
[2]陈哲,冯天谨.小波分析与神经网络结合的研究进展[J].电子科学学报,2000,22(3):496-502
[3]曾水玲,宋莺娇,徐蔚鸿.基于遗传算法的神经网络结构优化[J].吉首大学学报:自然科学版,2005,26(3):178-180
[4]石永奎,胡梦龙,刘阳,等.基于Hopfield神经网络的煤矿避灾硐室安全评价[J].煤炭技术,2015,34(12):177-179
[5]杜文莉,周仁,赵亮,等.基于量子差分进化算法的神经网络优化方法[J].清华大学学报:自然科学版,2012(3):331-335
