优化蚁群算法在无人机二维航迹中的应用

徐宏宇,孙洪俊,韩 毅(沈阳航空航天大学 电子信息工程学院，沈阳 110136)

优化蚁群算法在无人机二维航迹中的应用

徐宏宇,孙洪俊,韩 毅
(沈阳航空航天大学 电子信息工程学院，沈阳 110136)

为了有效提高无人机在执行侦察和攻击任务的效率,提出了诱发向导的蚁群算法的无人机航迹规划方法,将影响无人机飞行的敌方雷达侦测、飞行燃油代价、最大航程距离和高度代价四个因素进行了量化处理，建立了雷达威胁模型、燃油代价模型、最大航程距离限制模型和高度代价模型；并通过诱发向导的设立提高蚂蚁系统在局部搜索的效率，该仿真结果的分析证明该算法有效提高了无人机执行任务的效率。

无人机，蚁群算法；航迹规划；诱发向导；燃油代价；雷达侦测

随着航空科学技术的快速发展，无人机(UAV)被广泛应用。无论是在民用领域，还是在战场上，其具有体积小、造价低、使用方便、对作战环境要求低、战场生存能力较强等优势，几次局部战争中的优异表现，使得世界各国军队对无人机(UAV)高度重视。无人机(UAV)的航迹规划的主要问题包括任务需求、雷达威胁分布、燃油限制、最大航程距离和飞行高度。蚁群算法(ant colony op-timization)[1-3]是由意大利科学家Marco Dorigo等人在20世纪90年代初提出来的，是一种在图中寻找优化路径的机率型算法，其具有可靠性高、较强的鲁棒性和全局搜索能力等优势。但蚁群算法也存在缺点，即收敛速度慢、易于陷入局部最优、容易出现过早停滞。本文通过加入诱发向导优化其局部搜索效率，从而提高其在自由空间上获得更强的自适应的能力，以便获取最优航迹。

1 规划模型

无人机二维路径搜索[4-5]的影响因素主要包括四个方面：雷达侦测、飞机的最大载油量、最大航程距离限制和飞行高度。首先假定所有雷达的工作方式完全一致，并且无人机具有相同的雷达反射截面，于是可以得出无人机的反射雷达回波强度与其和雷达的距离的关系，即强度与距离的四次方成反比(1/d4)，雷达的侦测范围通常可以认为是圆球型，当飞机距离越近，被侦测到的概率就越大，在二维平面上，可以将雷区的侦测范围和威胁程度用同心圆来表示，雷达侦测的绝对威胁区域由同心圆的内圆来表示，内圆的面积表示雷达侦测的绝对威胁区域，由同心圆外圆的内部与内圆的外部之间的环形区域面积来表示非绝对禁止区域，被侦测到的概率定义为

(1)

其中p(m)为在m的时候被侦测到的概率，Rmin表征突防高度下绝对禁止区半径,依据情报给定;Rmax表征突防高度下非绝对禁止区半径,可作为威胁范围估计补偿加入，r表示无人机所处的位置到威胁点的距离的值，对于区域重叠部分,不同的雷达威胁点对于无人机的侦测概率计为pi(m),i=1,2,3,4,…,p(m)综合评价侦测概率则由以公式(2)求取。

(2)

然后将地形图划分为若干等大的方块，飞机沿着方块的边线和对角线飞行，可以到达与之相邻的任何一个点。那么无人机沿每条边或对角线飞行的雷达威胁代价Ja是飞过该边的积分：

(3)

其中，r(t)表示无人机到雷达的距离，p(m)表示雷达的侦测概率。为方便计算，将每条边均匀地分为9等分，取每一段与威胁点的距离来代替整条边的代价，Li是第i边的长度，这样第i条边的雷达威胁代价Ja为

(4)

其中N为雷达的个数。d1/10,i,j是第i条边上的1/10处到第j个雷达的距离。

另一方面，在假定无人机以恒定的速度在同一高度水平面飞行的情况下，无人机的燃料消耗和航迹的几何长度成正比，比例常数为c,可表示为

Jb,i=cLi

(5)

综合考虑上面两方面的因素，无人机第i条边的总代价为

Ji=kJa,i+(1-k)Jb,i

(6)

其中，k为安全性能与燃油性能的系数，可根据任务需求调整k的大小，k越接近1表示越重视燃油的使用情况，越接近0表示越重视危险性代价。其中M为边的条数。

(7)

设置最大航程距离值，即无人机航迹的最大有效值，路径规划的每一段距离La都应该实现,由式(8)所示，因此当航迹规划出一个路径时，如果超过最大值有效值时，认为航迹为无效，应重新规划。

L≤Lmax

(8)

常规的航迹规划问题需要考虑飞机的飞行高度，飞行高度可能直接导致穿越云层时遇见恶劣天气不能飞行，而本文主要针对的是小型无人机，飞行高度在百米以内，很大程度可以认为是在距离地面较低的高度上紧贴地表进行飞行，这样可以忽略天气的影响，只需对高山进行特定区域标定，无人机需要绕过此区域，无人机可以通过将高山模拟成雷达侦测的禁止区域进行躲避。

通过模型的建立，有效地将飞机最大载油量限制，雷达侦测，最大航程距离主要影响因素考虑到航迹规划中，为之后的优化蚁群算法提供求解条件，否则将无法进行有效求解。因此，合理、有效地建立模型是规划的关键。

2 蚁群算法的构造

2.1 诱发向导

蚁群算法[4-6]最初用于商旅问题[7](TSP)，M.Dorigo等人充分利用了蚁群觅食的过程与商旅问题之间的相似性，通过人工模拟蚂蚁觅食的过程，即通过个体之间的信息交流与相互协作最终找到从蚁穴到食物源的路径来求解商旅问题。原有的蚁群算法的路径搜索依据信息浓度和启发因子的概率选择，本文在原有的蚁群算法基础之上，通过加入诱发向导，以达到对蚁群算法的优化。将航迹规划简化在二维平面上，考虑到二维平面上是一个连续的集合，将无人机搜索的平面划分成有限个正方形的网络格，通过对这样的网络格不停搜寻节点，直到目标点，将所有搜索的节点连在一起，这便是所求的最优路线。以i节点为例，从节点i开始搜索，搜索的下一个节点必须是从其为中心组成的8个相邻节点中选择，但考虑实际搜索中需要前进性，剔除不满足条件的节点，由剩下的5个节点构成的扇形面才是需要考虑的节点，即如图1所示组成的黑色区域的节点。设节点i到目标节点j的距离为dij,则诱发向导为

λi=1/dij

(9)

图1 扇形面

这5个节点的启发因子的数值相差不大，在算法的初期容易导致盲目选择，不能够有效地到达目标节点。由公式9可知，某节点的诱发向导的大小与距离目标节点的距离成反比，加入诱发向导，可以有效提高搜索的效率。

2.2 信息素矩阵

将网络格依据其大小和起始点、目标点和威胁点的位置来规划二维地图，设其中空间的4个点坐标分别为(xmin,ymin)、(xmax,ymin)、(xmin,ymax)、(xmax,ymax),设网络格大小为G，则网络格共有行数h和共有列数v分别为

h=(ymax-ymin)/G

(10)

v=(xmax-xmin)/G

(11)

其中n为节点数，n=hv,坐标为(xi，yi)的网络格节点编号pi的计算公式为

(12)

2.3 启发函数

启发函数主要是用来提高节点选择效率，提高算法的收敛速度，加速算法的最小航迹。本文中以雷达的侦测为主，因此启发函数[8-10]的设计为威胁点的倒数，设置B个威胁点，第J个威胁点坐标为(xi,yi),则节点i到威胁点j的威胁代价表示为

εij=1/[(xi-xj)2+(yi-yj)2]2

(13)

根据式(13)求出节点i到所有威胁点的代价为

(14)

节点的启发函数等于总威胁代价的倒数，即ηi=1/εi，因此当节点威胁代价越小时，启发函数越大，选择效率越高，反之选择效率越低，启发函数的作用是加速算法收敛，但相对于信息浓度而言，所占比重如果过大，信息浓度将失去指引作用。

2.4 转移概率函数

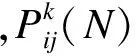
(15)

(16)

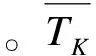
2.5 信息素轨迹更新与限制

迭代次数N每增加一次，路径上的信息素[11-15]就要挥发一次，用参数(1-e)表示信息素的挥发程度，所有蚂蚁完成一次迭代循环，各航迹段上信息的浓度根据式(17)和(18)作调整。

(17)

其中，Δτij(N)b表示第N次迭代中最小代价的蚂蚁所对应的航迹，和一般算法对蚂蚁进行对信息浓度增强不同，本文考虑最小代价航迹的信息浓度增强，这样更有效地提高算法收敛速度，但是可能出现某条边上信息素增长过快，因此设置区间把信息浓度限制在范围[τmin,τmax]内，以避免算法陷入停滞。

(18)

Q为常数，表示信息浓度增加强度系数，Lk表示第K只蚂蚁在本次循环里所走过的路程。Q、ρ根据求解规模确定其取值。固定迭代次数或者当解的变化不明显的时候停止计算。

3 航迹规划仿真验证示例

图2为二维等高线地形图，地形的大小为20 km×20 km,地形图中，出发点的坐标为(1,2)和目标点的坐标为(19.18)，图中每两个同心圆的圆心表示威胁点，即雷达所在的位置，图中一共选择了8个点来进行标记雷达的位置分别为(4,8)、(9,6)、(11,14)、(13,4)、(15,18)、(14,17)(15,10)和(19,14)。将雷达的侦测的绝对威胁区域用同心圆的内部圆覆盖的面积来表示，内部圆的半径为Rmin=2 km，由同心圆外圆的内部与内圆的外部之间的环形区域来表示非绝对禁止区域，外部圆的半径为Rmax=2.5 km。用矩形来表示不可穿越的高山区域，中心坐标分别为(15.7,6.5)，(16,5.5)宽度为1，中心坐标(5,8)宽度为4，长为6。

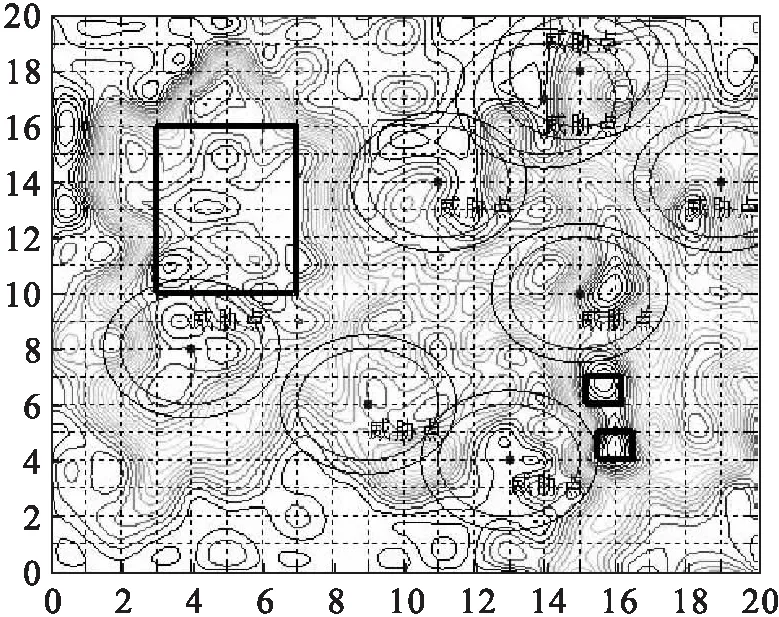
图2 等高线地图

无人机根据所处的地形、雷达侦测位置和燃油代价对目标节点进行路径搜索，用线段表示无人机的搜索路线，其中Nmax=100，m=29，α=1，β=0.25，γ=0.5,e=0.1,Q=15,R=4，G=1，Lmax=35，K=0.5,C=1，图3为普通蚁群算搜索的路线图，图4为加入了诱发向导的蚁群算法，根据扇形区域提高了搜索效率，达到优化路径的目的。

图3 改进前

图4 改进后

4 结论

通过使用MATLAB仿真生成的路径图进行对比，从图3上可以看出，普通的蚁群算法为了躲避威胁点，选择以牺牲时间和路程为代价，采取远距离绕行雷达威胁点的方式进行路径搜索，虽然也可以实现路径搜索，但是其无法满足实际战场对无人机的高效、快捷的需要。图4为本算法的结果，可以看出在无人机路径规划上，加入诱发向导之后，算法的收敛速度得到了保证，并且通过设置最优路径的信息浓度更新策略和范围，不仅提高算法速度并且避免了算法陷入局部最优及出现停滞的问题，有效提高局部搜索的效率，尤其是在路径的选择上，提供了一条捷径优化路径来实现无人机对目标的路径搜索，达到了路径优化的要求。

[1] DORIGO M,MANIEZZO V,COLORNI A.Ant system:optimization by a colony of coorperating agents[J].IEEE Transaction on Systems,Man and Cybernetics-Part B,1996:26(1):29-41.

[2] 段海滨,马冠军，王道波,等.一种求解连续空间优化问题的改进蚁群算法[J].系统仿真学报，2007,19(5)：974-977.

[3] 温文波,杜维.蚁群算法概述[J].石油化工自动化，2002(1)：19-22.

[4] RANDALL M,LEWIS A.A parallel implementation of ant colony optimization[J].Journal of Parallel and Distributed Computing,2002,69(9):1421-1432.

[5] 冯琦,周德云.军用无人机发展趋势[J].电光与控制,2003,10(1):9-13.

[6] KROZEI J,DOMINICK A.Navigation path planning for au-tonomous aircraft:voronoi diagram approach[J].Journal ofGuidance,Control,and Dynamics,1990,13(3):1152-1154.

[7] ZHANG WENDONG,BAI YANPING.The incorporation of an effieient initialization method and Parameter adaptation using self-oranizing maps to solve the TSP[J].Applied Mathematics and Computation,2006,172(1)：603-623.

[8] EUN Y,BANG H.COOPERATIVE TASK ASSIGNMENT.Track planning of multiple unmanned aerial vehicles using genetic algorithms[J].Journal of Aircraft,2009,46(1):338-343.

[9] 王万良.人工智能及其应用(第3版)[M].北京：高等教育出版社，2016：248-257.

[10]刘玉军,张行知,蔡猛,等.基于监测任务的多旋翼无人机路径规划[J].中国电子科学研究院学报,2017,12(1):20-24.

[11]陈海,何开锋,钱炜祺.多无人机协同覆盖路径规划[J].航空学报,2016,37(3):928-935.

[12]符小卫,程思敏,高晓光.无人机协同中继过程中的路径规划与通信优化[J].系统工程与电子技 术,2014,36(5):890-894.

[13]李士勇,李研.智能优化算法原理与应用[M].哈尔滨：哈尔滨工业大学出版社，2012:47-54.

[14]朱黔,周锐.具有持续侦察时间约束的协同航路规划[J].北京航空航天大学学报，2016，42(10):2130-2138.

[15]齐乃明,孙小雷,董程,等.航迹预测的多无人机任务规划方法[J].哈尔滨工业大学学报，2016,48(4):32-36.

UAV2Dpathplanningbasedonantcolonyoptimizationalgorithm

XU Hong-yu，SUN Hong-jun，HAN Yi
(College of Electronics and Information Engineering,Shenyang Aerospace University,Shenyang 110136,China)

To effectively improve the efficiency of unmanned aerial vehicle (UAV) in reconnaissance and attacking missions,a UAV path planning method based on guided ant colony algorithm is proposed.First,the four factors (i.e.enemy radar detection,flight fuel cost,maximum range and height cost) that affect the UAV flight are quantified.Then,the models of radar threat,the fuel cost,the maximum range limit,and the altitude cost are built respectively.And the efficiency of the ant system in local search is improved by setting the guidance factor.The analysis of the simulation results shows that the algorithm can effectively improve the efficiency of the UAV missions.

UAV;ant colony optimization algorithm;path planning;evoked guidance;fuel cost;radar detection

2017-07-20

徐宏宇(1965-)，男，辽宁沈阳人，副教授，主要研究方向：信息获取与处理，E-mail：413945957@qq.com；孙洪俊(1987-)，男，辽宁鞍山人，硕士研究生，主要研究方向：信息获取与处理，E-mail:369092349@qq.com。

2095-1248(2017)06-0078-05

V21

A

10.3969/j.issn.2095-1248.2017.06.013

刘划 英文审校：齐义文)