任意形状声学黑洞的简化设计方法

许卫锴，张 蒙，王 伟 (.沈阳航空航天大学 航空航天工程学部(院)，沈阳 036；.沈阳建筑大学 土木工程学院，沈阳 068)

任意形状声学黑洞的简化设计方法

许卫锴1，张 蒙1，王 伟2
(1.沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136；2.沈阳建筑大学 土木工程学院，沈阳 110168)

提出一种简化的任意形状声学黑洞设计方法。利用比例映射变换，可以消除传统声学变换方法所导致的材料参数的高度各向异性，降低声学黑洞吸收体的制作成本。数值结果表明，该模型可以实现复杂形状下声波的显著吸收，证明了任意形状声学黑洞的有效性。该工作将对声学能量吸收和噪声控制提供一定的理论依据。

声学黑洞；任意形状；比例映射；声学变换

波的吸收问题一直以来都是人们研究的重点，并在多个学科都得到了广泛地关注，如光学、微波、声学、热学等领域。由于其惊人的吞噬能力，很多学者用“黑洞”的概念来形容完美的吸收体，并进行了广泛的研究。然而对于传统的黑洞设计来说，无论是吸波材料或是吸波结构都存在着各自的局限性，或者受限于特殊的入射角度[1-2],或者只具有非常窄的带宽[3]。因此，研究宽频带、高吸收的黑洞结构成为一个重要的课题。

近年来，一种基于“有效势(Effective potential)”概念的黑洞结构得到了研究人员的关注。通过合理设计材料的参数分布，可以实现折射率随位置变化的函数式分布[4]，从而形成类似于势力场的空间，最终达到控制波的传播路径的目的。第一个光学黑洞由Narimanov等人提出[5]，并很快得到了实验验证[6-8]。而利用光波与声波方程的相似性，与光学黑洞类似的声学黑洞也得到了关注，并由理论证实[9]和实验验证[10]。随后，声学黑洞得到了大量的研究，例如Song等人利用超材料实现声相干完美吸收器[11]，Naify[12]和Elliott[13]利用梯度材料设计了全方位的水下完美吸收体，Cheng等人利用均匀的各向异性超材料设计了一个二维宽频带的全方位声学吸收体并完成实验验证[14]，Hu等人则利用坐标变换方法设计了弹性波的黑洞结构[15]。

然而，目前存在的声学黑洞大多数都局限于规则的圆形结构，因此发展任意形状的声学黑洞变得非常重要。Wei等人用传统的声学变换方法设计了任意形状的声学黑洞[16]，但该方法会导致严重的各向异性，使得黑洞难以实现。基于此，本文提出了一种简化的任意形状声学黑洞设计方法，利用比例映射变换可以避免传统声学变换方法所导致的材料参数的高度各向异性，降低声学黑洞吸收体的制作成本。本文给出了3种形状的黑洞结构，结果表明，该模型可以实现复杂形状下声波的显著吸收，证明了任意形状声学黑洞的有效性。

1 理论模型

对于如图1(a)所示二维圆形黑洞结构，基于“有效势”的折射率分布可以表示为[4]

(1)

式中n0为背景介质的折射率，R1,R2分别为黑洞内核和黑洞包覆层的半径。折射率随半径的变化可以使得声波在其中传播时由外而内改变方向，就好像声波在势力场中在有势力的作用下向着低势能的方向前进。为了简单起见，圆形声学黑洞结构的参数分布可以参照变换光学和变换声学的关系，将声波方程中的弹性参数和Maxwell方程中的电磁参数相对比得到[5,9,17-18]。

(2)

其中ρ0,κ0分别表示背景材料的密度和弹性模量。

当黑洞结构的横截面由闭合的任意曲线r=R0(θ)构成时，如图1(b)所示，与隐身斗篷类似，也可以看作是空间的变换。一般来说，隐身斗篷离不开空间压缩，而黑洞的变形则更像把原来的圆环拉扯而成的变形区域。对比图1(a)和1(b)中的曲线，其中每一对都相差R0(θ)的倍数，因此任意形状的黑洞结构可以采用径向的比例映射来变换得到。

图1 黑洞结构简图

引入比例因子

ρ=r,ρ′=rR0(θ′)

(3)

则映射关系如式(4)所示。

ρ′=ρR0(θ′),θ′=θ,z′=z

(4)

根据式(2)，任意形状黑洞中弹性参数的表达式为

(5)

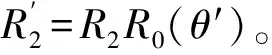
(6)

这意味着材料的弹性模量为非均匀但各向同性的。无论曲线R0(θ)选取任何函数，该模型都可以形成有效势从而引导声波被吸收。

2 数值仿真与分析

为了验证模型的有效性，本文对3种不同形状的黑洞结构进行了全波模拟。背景介质选取为水，密度和模量分别为ρ=998 kg/m3,κ=2.19×109Pa。半径分别选为R1=0.2 m，R2=0.5 m。入射波频率为16 kHz，分别考虑了平面波和高斯波两种情况。为了简单起见，我们采用吸收边界来代替内核的耗散材料。3种曲线的方程如式(7)所示。

CaseA:R0(θ)=0.7+0.1sin(θ)+0.1sin(3θ)+0.1cos(5θ)

CaseB:R0(θ)=[12+2cos(θ)+sin(2θ)-2sin(3θ)]/20

CaseC:R0(θ)=1+0.1sin(θ)+0.2sin(3θ)

(7)

图2显示了式(7)中算例A的声压场分布。其中图2(a)和2(c)分别表示仅有耗散材料时平面波和高斯波的传播情况。当入射波为平面波时，很明显只有位于吸声边界范围内的声波被吸收，并在其身后留下了一个与吸收边界相当大小的声阴影部分。而当入射波为高斯波时，由于高斯波的位置高于吸收边界，因此几乎没有被吸收。图2(b)和2(d)显示了放置黑洞结构时的声压场。可以看出，入射波为平面波时，当波通过黑洞区域后，吸声区域明显大于吸收边界，并且高斯波也被拖拽而偏离原来的轨迹，最终被黑洞吞噬。这证明了该黑洞设计的有效性。

图2 算例A在平面波和高斯波下的声压场分布

值得注意的是，在声压场中可以观察到有散射现象的发生，这是由不规则的边界引起的，尤其是曲率变化剧烈的地方。此外，由图2(b)和2(d)可以看出，在黑洞边界曲线上存在反向扭曲的位置会有一小部分声波逃逸出黑洞范围，这是由于由比例映射产生的“有效势”相对于曲线的扭曲度较为温和，不足以完全控制波的轨迹。但是，因为声波的轨迹已经被改变了，因此当逃逸的声波再次遇上黑洞边界的时候将被再次吸入。

为了验证上述分析，图3显示了式(7)中算例B的声压场分布。图3(a)和3(c)分别表示仅有耗散材料时平面波和高斯波的传播情况，图3(b)和3(d)显示了放置黑洞结构时的声压场。可以看出，由于算例B的曲线较为平缓，在黑洞结构大幅增加声波吸收的同时，散射现象也得到了较好的改善。

图3 算例B在平面波和高斯波下的声压场分布

此外，式(7)中算例C的声压场分布如图4所示。为了节省篇幅，文中仅仅显示了存在声学黑洞时的声压场，同样可以得到以上结论。

图4 算例C黑洞结构下的声压场分布

特殊的，当曲线表达式为R0(θ)=1时，模型将退化为一个标准的圆形黑洞，相应的声压场如图5所示，与文献[9]中的结果一致。

图5 圆形黑洞声压场

3 结论

基于声学变换的思想，本文提出一种简化的任意形状声学黑洞设计方法。区别于声学隐身斗篷的空间压缩，当引入径向比例映射时，可消除传统声学变换方法所导致的材料参数高度各向异性问题，得到非均匀但各向同性的声学黑洞，降低声学黑洞吸收体的制作成本。通过3种不同形状的算例表明，该模型可以实现复杂形状下声波的显著吸收，证明了任意形状声学黑洞的有效性。本文的工作将对声波吸收和噪声控制提供一定的理论依据。

[1] COLLIN S,PARDO F,TEISSIER R,et al.Efficient light absorption in metal-semiconductor-metal nanostructures[J].Appl.Phys.Lett,2004,85(2):194-196.

[2] KUO M L,POXSON J,KIM Y S,et al.Realization of a near-perfect antireflection coating for silicon solar energy utilization[J].Opt.Lett,2008,33(21):2527-2529.

[3] LANDY N I,SAJUYIGBE S,MOCK J J,et al.Perfect metamaterial absorber[J].Phys.Rev.Lett,2008,100(20):207402.

[4] MORSE P,FESHBACH H.Methods of Theoretical Physics[M].Mc.Graw-Hill,1953.

[5] NARIMANOV E E,KILDISHEV A V.Optical black hole:Broadband omnidirectional light absorber[J].Appl.Phys.Lett,2009,95(4):041106.

[6] CHENG Q,CUI T J,JIANG W X,et al.An omnidirectional electromagnetic absorber made of metamaterials[J].New J.Phys,2010,12(6):063006.

[7] LU W,JIN J,LIN Z,et al.A simple design of an artificial electromagnetic black hole[J].J.Appl.Phys,2010,108(6):064517.

[8] ZHOU J,CAI X,CHANG Z,et al.Experimental study on a broadband omnidirectional electromagnetic absorber[J].J.Opt,2011,13(8):085103.

[9] LI R,ZHU X,LIANG B,et al.A broadband acoustic omnidirectional absorber comprising positive-index materials[J].Appl.Phys.Lett,2011,99(19):193507.

[10]CLIMENT A,TORRENT D,SANCHEZ-DESEHA J.Omnidirectional broadband acoustic absorber based on metamaterials[J].Appl.Phys.Lett,2012,100(14):144103.

[11]SONG J Z,BAI P,HANG Z H,et al.Acoustic coherent perfect absorbers[J].New J.Phys,2014,16(3):033026.

[12]NAIFY C J,MARTIN T P,LAYMAN C N,et al.Underwater acoustic omnidirectional absorber[J].Appl.Phys.Lett,2014,104(7):073305.

[13]ELLIOTT A S,VENEGAS R,GROBY J P,et al.Omnidirectional acoustic absorber with a porous core and a metamaterial matching layer[J].J.Appl.Phys,2014,115(20):204902.

[14]GU Z M,JIANG X,LIANG B,et al.Experimental realization of broadband acoustic omnidirectional absorber by homogeneous anisotropic metamaterials[J].J.Appl.Phys,2015,117(7):074502.

[15]CHANG Z,HU G K.Elastic wave omnidirectional absorbers designed by transformation method[J].Appl.Phys.Lett,2012,101(5):054102.

[16]WEI Q,CHENG Y,LIU X J.Acoustic omnidirectional superabsorber with arbitrary contour[J].Appl.Phys.Lett,2012,100(9):094105

[17]Chen H Y,Chan C T.Acoustic cloaking in three dimensions using acoustic metamaterials[J].Appl.Phys.Lett,2007,91(18):183518.

[18]Chen H Y,Chan C T.Acoustic cloaking and transformation acoustics[J].J.Phys.D:Appl.Phys,2010,43(11):113001.

Simplifieddesignmethodofacousticblackholeswitharbitraryshapes

XU Wei-kai1，ZHANG Meng1，WANG Wei2
(1.Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China;2.School of Civil Engineering,Shenyang Jianzhu University,Shenyang 110168,China)

A simple model was presented to investigate two-dimensional acoustic black holes with arbitrary shapes.In the model,a proportional mapping was considered to eliminate the high anisotropy of parameters caused by traditional transformation acoustics and reduce production cost of acoustic black holes absorber.Numerical simulations show that remarkable absorption of acoustic wave is realized under complicated situation.The proposed method can control the acoustic absorption with arbitrary geometries.This will provide the theoretical support for acoustic energy absorption and noise control.

acoustic black holes;arbitrary shapes;proportional mapping;acoustic transformation

2017-06-26

国家自然科学基金(项目编号：11302135,51308357,11672187)；辽宁省自然科学基金(项目编号：201602572,201602627)；辽宁省高等学校优秀人才支持计划(项目编号：LJQ2014019,LJQ2015091)。

许卫锴(1979-)，男，山东淄博人，副教授，博士，主要研究方向：超材料微结构优化设计，声子晶体，E-mail：wkxu@sau.edu.cn。

2095-1248(2017)06-0022-05

O429;TB535

A

10.3969/j.issn.2095-1248.2017.06.004

刘划 英文审校：赵欢)