圆柱结构涡激振动拖曳水池实验研究
2017-12-27高喜峰周丽丹徐万海马烨璇吴梦宁
高喜峰, 周丽丹, 徐万海, 马烨璇, 吴梦宁
(天津大学 水利工程仿真与安全国家重点实验室, 天津 300072)
圆柱结构涡激振动拖曳水池实验研究
高喜峰, 周丽丹, 徐万海, 马烨璇, 吴梦宁
(天津大学 水利工程仿真与安全国家重点实验室, 天津 300072)
柔性圆柱涡激振动特性已得到人们广泛关注,然而横流向与顺流向振动耦合问题仍有待进一步研究。设计了柔性圆柱涡激振动拖曳水池模型实验,圆柱模型的长径比为195.5、质量比为1.82,实验观测了圆柱结构横流向、顺流向涡激振动特性,并分析了横流向与顺流向两个方向涡激振动的耦合现象。通过应变传感器测量结构振动信息,利用模态分析法对实验数据进行处理,实验发现横流向与顺流向涡激振动耦合现象显著,特别是不同测点处的运动轨迹出现了“8字形”、倒置的“泪滴形”、 “口唇形”等多种复杂形式。
涡激振动; 水池实验; 柔性圆柱; 流-固耦合
一定流速下置于流场中的圆柱结构后缘会出现交替的漩涡脱落,诱使结构在横流向(Cross-Flow,CF)与顺流向(In-Line,IL)发生振动,结构振动又反作用于流场,这种典型的流-固耦合现象称之为“涡激振动(Vortex-Induced Vibrations, VIV)。VIV是海洋工程中的立管、系泊缆、海底悬跨管道等圆柱结构疲劳损伤的重要诱因。现阶段,相关柔性圆柱的涡激振动研究已得到了国内外学者广泛关注[1-8]。
模型实验研究长久以来一直得到学者们的青睐,其不仅能够为校准涡激振动预报模型提供基准数据,还可深入直观的认识涡激振动现象。Chaplin等[9]实验观测了阶梯来流海洋立管涡激振动响应特性,发现IL方向模态权重幅值可达0.16D(D为立管直径),CF方向模态权重幅值亦达到了0.53D。Trim等[10]在挪威Marintek的海洋工程水池中对一根长38 m的立管模型进行了均匀流下的涡激振动实验研究。Lie等[11]设计了剪切来流条件下90.0 m长的柔性立管涡激振动实验,并阐述了实验数据分析的模态分析法。Huera-Huarte等[12-13]通过开展长细比为94.0的柔性圆柱涡激振动实验,研究了CF与IL方向的运动轨迹,并分析了CF和IL位移的相位差,给出了平均拖曳力随约化速度及立管振动幅值的变化规律。宋吉宁等[14]在室内拖曳水池中实验研究了均匀来流下大长径比(1 750)立管模型的涡激振动特性,通过光纤光栅传感器测量立管模型在横流向和顺流向的应变,并通过模态分析法获得模型振动响应位移。顾继俊等[15]在实验水槽中开展了长径比为74.4的柔性立管涡激振动实验,利用广义积分变换方法计算了不同顶部张力情况下立管的拖曳力系数与升力系数随约化速度的变化规律。
虽然有关涡激振动的研究已取得大量成果,但由于柔性圆柱涡激振动十分复杂,有关横流向与顺流向涡激振动的耦合机制仍不清晰,相关实验研究仍有待进一步深入开展。本文设计了柔性圆柱拖曳水池室内模型实验,圆柱模型外径20 mm、长径比195.5、质量比1.82。实验观测了横流向、顺流向涡激振动特性,重点分析了横流向与顺流向两个方向涡激振动的耦合现象。
1 实验设计
实验在天津大学水利工程仿真与安全国家重点实验室的拖曳水池中完成,水池长137.0 m,宽7.0 m,深3.3 m。实验圆柱模型内芯为薄壁钢管,外表面覆盖热塑管,目的是保证圆柱模型表面光滑,防止应变片和导线等测量仪器暴露水中,并起到绝缘作用,最终圆柱外径为20 mm,其他结构参数如表1所示。圆柱模型通过万向节与钢架相连,钢架通过螺栓与拖车固定,圆柱模型右端通过钢丝绳连接弹簧和张紧器,改变张紧器可实现不同轴向力的实验工况,为了保证圆柱端部来流的平稳性,实验设计了导流板,详细的实验装置如图1所示。

表1 圆柱模型参数Tab.1 Physical property for the cylinder model in experiment
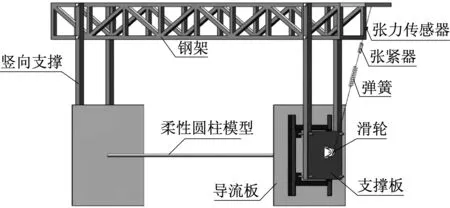
图1 实验布置示意图Fig.1 Schematic of the experimental set-up
本文实验中,圆柱结构承受四种轴向力,分别为T=0 N、50 N、100 N和150 N。通过拖车的匀速拖动模拟均匀流,拖车速度范围为0.2 m/s~1.0 m/s,速度间隔为0.1 m/s,共9个来流速度工况。实验采用应变片测量结构横流向与顺流向应变信息,应变片粘贴于钢管表面,本实验圆柱模型共有五个测点,从左至右分别为A、B、C、D、E,测点将管道模型均分为6等份,实验数据的采样频率为50 Hz,采样时间为40 s。本文共计开展36组实验工况。
首先,测量圆柱模型静水中的固有频率。在水中开展自由衰减实验,横流向和顺流向分别施加一个初始位移,让圆柱结构自由振动。测得圆柱模型在水中的一阶固有频率f1,并与理论值进行对比,如表2所示。可发现固有频率的理论结果与实验测量结果差异很小,进一步证明了实验仪器设备精度良好、可信度较高。

表2 圆柱模型静水中固有频率Tab.2 Natural frequency of cylinder model in still water
2 数据分析方法
本实验采用应变片测量圆柱结构的振动信息,难以全面反映涡激振动的规律特性,需运用模态分析法将应变信号转化为位移信息。横流向与顺流向两个方向数据处理方法相同,在此仅以横流向为例进行阐述。
根据模态分析法基本原理,圆柱结构横流向涡激振动位移可表示为

(1)
式中:t为时间;z为轴向坐标;x为顺流向坐标;y为横流向坐标;ωn(t)为权重系数;φn(z)为模态函数;n为圆柱模型横流向涡激振动模态阶次;N为能够准确描述振动位移所需的模态数目;L为圆柱总长度。本实验圆柱模型两端为简支边界,因此,

(2)
根据几何关系,圆柱模型曲率计算公式为
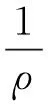
(3)
由于y′为小量,式(3)可简化为
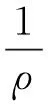
(4)
根据曲率与应变之间的关系,得到:
(5)
式中:ε为应变;R为薄壁钢管半径;设应变片的数量为M;圆柱模型振动位移可用N个模态阶次叠加,式(5)可简化为
AW=B
(6)
其中:
模态分析法选取模态数目N不大于测点数目M,采用最小二乘法求解权重系数,公式如下:
W=[ATA]-1ATB
(10)
有关模态分析法对应变信号处理的详细理论可参考文献[9-11]。
3 实验结果分析
本部分首先实验观测横流向与顺流向涡激振动特性,而后在此基础上进一步分析横流向与顺流向两个方向涡激振动的耦合现象。横坐标选取无量纲的约化速度,其定义为Vr=U/f1D,U为拖车速度,f1为固有频率理论值,D为圆柱模型外径。
3.1 横流向涡激振动
横流向涡激振动是引起结构疲劳损伤的主要因素。图2描述了四种轴向力工况下控制模态随约化速度的变化图像。可以发现:随着约化速度的增加,高阶模态逐步被激发;当Vr<16.0时,四种轴向力工况控制模态均为1阶,随着约化速度的增加控制模态逐渐转化为2阶。本文实验的横流向涡激振动最大控制模态为2阶。
图3描述了控制频率随约化速度的变化情况。可以发现约化速度的增加会导致控制频率呈现逐步变大趋势。在Vr=16.0附近控制频率突然发生跳跃,原因是由于控制模态由1阶转化为2阶引起的。St数是涡激振动的一个重要参数,一般可表示为
St=fsD/U
(11)
式中:fs为漩涡脱落频率,一般情况下,当VIV发生时,可以假定漩涡脱落频率fs与横流向VIV的控制频率相等,于是可根据实验获得的横流向结构振动控制频率数据做以线性拟合,得到本文实验的斯特罗哈数St=0.165,与Chaplin等实验中的0.17和Huera-Huarte等实验中的0.16十分接近。

图2 横流向控制模态随约化速度变化图Fig.2 CF dominate mode number versus reduced velocity

图3 横流向控制频率随约化速度变化图Fig.3 CF dominate frequency versus reduced velocity
最大位移均方根是描述结构涡激振动响应强弱的重要指标,图4为利用模型外径无量纲化的位移均方根与约化速度关系图。可以看出横流向涡激振动位移均方根小于0.60D,轴向力对最大位移均方根的影响并不明显。当4.0 图4 横流向最大位移均方根随约化速度变化图Fig.4 CF Max RMS displacement versus reduced velocity 图5 横流向最大应变均方根随约化速度变化图Fig.5 CF Max RMS strain versus reduced velocity 顺流向涡激振动因响应幅值较小而往往受到忽视,但是其比横流向涡激振动更加容易被激发,振动频率约为横流向振动频率的2倍~3倍,因此顺流向涡激振动对柔性圆柱的疲劳破坏有十分重要的影响。图6描述了顺流向涡激振动控制模态随约化速度的变化,可以发现:随着约化速度的增加,顺流向涡激振动高阶模态逐步被激发,与横流向规律类似,顺流向最大控制模态为3阶。同时发现一个有趣的现象,轴向力较大时,顺流向涡激振动高阶模态更容易被激发,如约化速度14.0和20.0附近。 图7描述了顺流向控制频率随约化速度的变化。在Vr=10.0、20.0附近,控制频率出现跳跃,此时为顺流向涡激振动控制模态转化阶段,分别为1阶转化为2阶,2阶转化为3阶的区域。 图8为顺流向涡激振动最大位移均方根随约化速度变化的图像。本文实验的顺流向涡激振动位移均方根较小,一般小于0.30D。 图6 顺流向控制模态随约化速度变化图Fig.6 IL dominate mode number versus reduced velocity 图7 顺流向控制频率随约化速度变化图Fig.7 IL dominate frequency versus reduced velocity 图8 顺流向最大位移均方根随约化速度变化图Fig.8 IL Max RMS displacement versus reduced velocity 图9描述了不同轴向力情况下顺流向最大应变均方根随约化速度的变化。可发现顺流向应变均方根随着约化速度的增加变化的比较缓慢。对数据进行二次曲线拟合,同样得到了顺流向应变与约化速度的函数关系,拟合的方程为ε_IL_max_RMS=3.18Vr+0.065Vr2,近似于线性变化。 图10为横流向和顺流向控制模态之间的比值随约化速度的变化图像,可发现控制模态CF/IL的比值均小于1.0,即顺流向控制模态转化比横流向需要的流速小,这是由于顺流向拖曳力频率为横流向升力频率的2倍,因此顺流向振动更容易激发高阶模态。当Vr<10.0,横流向和顺流向的控制模态均为1阶;在Vr=10.0附近顺流向的控制模态变为2阶,横流向控制模态仍为1阶,T=100 N和T=150 N顺流向涡激振动控制模态跳跃到3阶,此时横流向控制模态仍为1阶;当Vr=15.0时,横流向控制模态转化为2阶,此时横流向和顺流向的控制模态均为2阶,随着流速的增加,T=100 N和T=150 N两种情况的顺流向的控制模态转化为3阶,对应横流向控制模态为2阶。 图9 顺流向最大应变均方根随约化速度变化图Fig.9 IL Max RMS of strain versus reduced velocity 图10 CF/IL控制模态随约化速度变化图Fig.10 CF/IL dominate mode number versus reduced velocity 图11描述了横流向和顺流向控制频率的比值随约化速度的变化。可以看到:当5.0 图12为两个方向振动位移比值随约化速度变化的图像。可发现横流向与顺流向的位移均方根的比值均大于1.0。统计所有实验工况数据,得到横流向最大位移均方根平均为顺流向3.09倍。 图11 CF/IL控制控制频率随约化速度变化图Fig.11 CF/IL dominate frequency versus reduced velocity 图12 CF/IL最大位移均方根随约化速度变化图Fig.12 Max RMS CF/IL displacement versus reduced velocity 图13描述了横流向与顺流向的最大应变均方根的比值。得到横流向的最大应变均方根平均为顺流向的2.21倍。在模态转化区域外部,横流向与顺流向的最大应变均方根比值在均值上方,在模态转化区域10.0 图13 CF/IL最大应变均方根随约化速度变化图Fig.13 Max RMS CF/IL strain versus reduced velocity 为了更加深刻的理解涡激振动横流向和顺流向的耦合作用,图14给出了T=150 N时,不同流速下,柔性圆柱模型A、B、C、D、E五个测点处的x-y运动轨迹,此时的横坐标为流速,可以看出在流速为0.2 m/s时,五个测点处的运动轨迹均为“8字形”;随着流速增加到0.3 m/s,0.4 m/s时,“8字形”变得不明显,取而代之的是倒置的“泪滴形”;随着流速进一步增大,横流向与顺流向之间的响应幅值差距变小,五个截面x-y轨迹均为混乱的“椭球形”;当流速为0.7 m/s和0.8 m/s时,五个截面x-y轨迹十分混乱;流速增大到0.9 m/s和1.0 m/s时,五个截面的x-y轨迹不尽相同,出现了“口唇形”,同时“8字形”亦再次出现。 图14 不同测点处x-y运动轨迹(T=150 N)Fig.14 Trajectory profiles at different current speed and different positions with T=150 N 本文开展了外径20 mm、长径比195.5、质量比1.82的柔性圆柱拖曳水池涡激振动模型实验,通过模态分析法将应变信号转化为位移信息,观测了横流向和顺流向涡激振动特性,分析了横流向与顺流向两个方向涡激振动的耦合现象,实验结果表明: (1) 横流向VIV的控制模态最高为2阶,顺流向为3阶,柔性圆柱涡激振动实验的斯托罗哈数为0.165; (2) 横流向涡激振动位移均方根可达0.60D、而顺流向为0.30D,横流向的最大位移均方根平均为顺流向的3.09倍、横流向的最大应变均方根平均为顺流向的2.21倍; (3) 通过观测五个测点处的x-y轨迹,运动轨迹呈现了“8字形”、倒置的“泪滴形”、混乱的“椭球形”、“口唇形”等多种形式。 上述取得的研究结论可进一步丰富柔性圆柱涡激振动知识体系,具有重要的理论价值和工程意义。 [1] VANDIVER J K. Dimensionless parameters important to the prediction of vortex induced vibration of long, flexible cylinders in ocean currents [J]. Journal of Fluids and Structures, 1993(7):423-455. [2] SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations [J]. Journal of Fluids and Structures, 2004, 19: 389-447. [3] GABBAI R D, BENAROYA H. An overview of modeling and experiments of vortex -induced vibration of circular cylinders [J]. Journal of Sound and Vibration, 2005, 282: 575-616. [4] WILLIAMSON C H K, GOVARDHAN R. A brief review of recent results in vortex-induced vibrations [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 713-735. [5] 薛鸿祥,唐文勇,张圣坤.非均匀来流下深海立管涡激振动响应研究[J]. 振动与冲击,2007,26(12):10-13. XUE Hongxiang, TANG Wenyong, ZHANG Shengkun. Prediction of vortex-induced vibration of deep water riser in non-uniform current [J]. Journal of Vbration and Sock, 2007, 26(12): 10-13. [6] 曹淑刚,黄维平,顾恩凯. 考虑流固耦合的弹性圆柱体涡激振动研究[J]. 振动与冲击,2015,34(1):58-62. CAO Shugang, HUANG Weiping, GU Enkai. Vortex-induced vibration of an elastic cylinder considering fluid-structure interaction [J]. Journal of Vbration and Sock, 2015, 34(1): 58-62. [7] 高云,任铁,付世晓,等. 柔性立管涡激振动响应特性试验研究[J]. 振动与冲击,2015,34(17):6-11. GAO Yun, REN Tie, FU Shixiao, et al. Tests for response characteristics of VIV of a flexible riser [J]. Journal of Vibration and Shock, 2015, 34(17): 6-11. [8] 谷家扬,杨琛,朱新耀,等.质量比对圆柱涡激特性的影响研究[J]. 振动与冲击,2016,35(4):134-140. GU Jiayang, YANG Chen, ZHU Xinyao, et al. Influences of mass ratio on vortex induced vibration characteristics of a circular cylinder [J]. Journal of Vibration and Shock, 2016, 35(4): 134-140. [9] CHAPLIN J R, BEARMAN P W, HUERA-HUARTE F J, et al. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current [J]. Journal of Fluids and Structures, 2005, 21: 3-24. [10] TRIM A D, BRAATEN H, LIE H, et al. Experimental investigation of vortex-induced vibration of long marine risers [J]. Journal of Fluids and Structures, 2005, 21: 335-361. [11] LIE H, KAASEN K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow [J]. Journal of Fluids and Structures, 2006, 22: 557-575. [12] HUERA HUARTE F J, BEARMAN P W. Wake structures and vortex-induced vibrations of a long flexible cylinder-Part 1: Dynamic response [J]. Journal of Fluids and Structures, 2009, 25(6):969-990. [13] HUERA HUARTE F J, BEARMAN P W. Wake structures and vortex-induced vibrations of a long flexible cylinder-Part 2: Drag coefficients and vortex modes [J]. Journal of Fluids and Structures, 2009, 25(6):991-1006. [14] SONG Jining, LU Lin, TENG Bin, et al. Laboratory tests of vortex-induced vibrations of a long flexible riser pipe subjected to uniform flow [J]. Ocean Engineering, 2011, 38:1308-1322. [15] GU J J, VITOLA M, COELHO J, et al. An experimental investigation by towing tank on VIV of a long flexible cylinder for deepwater riser application [J]. Journal of Marine Science & Technology, 2013, 18(3):358-369. Towingtanktestsforvortex-inducedvibrationsofacircularcylinder GAO Xifeng, ZHOU Lidan, XU Wanhai, MA Yexuan, WU Mengning (State Key Lab of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin, 300072, China) Till now, a large number studies on vortex-induced vibrations (VIV) of flexible cylinders have been performed, but the in line (IL)-cross flow (CF) coupled VIV still needs to study further. Here, a towing tank test of VIVs of a circular cylinder was designed. The aspect ratio (length/diameter) of the cylinder model was 195.5 and its mass ratio was 1.82. With this cylinder model, the coupling effect between IL and CF VIVs was analyzed. The structural vibration was measured by means of strain gages and the modal analysis method was used to analyze the test data. It was shown that the coupling phenomenon between IL-VIV and CF-VIV is very obvious; the trajectories of different measured points have many complex forms, such as, “8-shape”, “inverted tear drop” and “mouth-shape”. vortex-induced vibration; towing tank test; flexible cylinder; fluid-structure interaction 国家自然科学基金(51379144;51479135;51679167);国家自然科学基金创新研究群体科学基金(51621092);国家重点基础研究计划-973计划(2014CB046801) 2016-03-21 修改稿收到日期:2016-09-22 高喜峰 男,副教授,硕士生导师,1976年生 徐万海 男,副教授,硕士生导师,1981年生。E-mail:xuwanhai@tju.edu.cn TV312 A 10.13465/j.cnki.jvs.2017.23.019


3.2 顺流向涡激振动


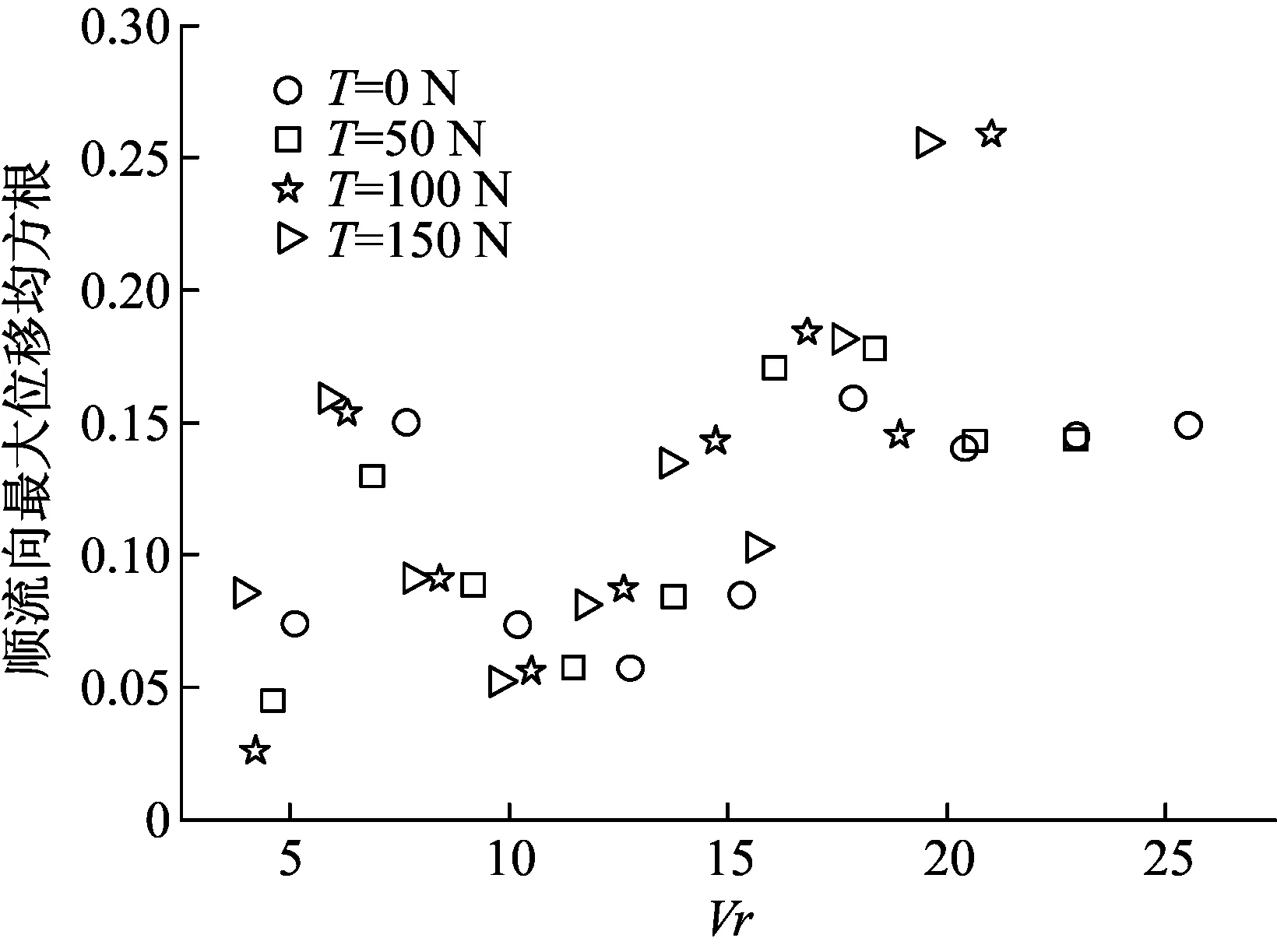
3.3 横流向/顺流向耦合作用
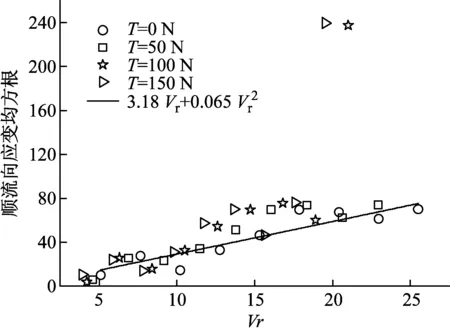

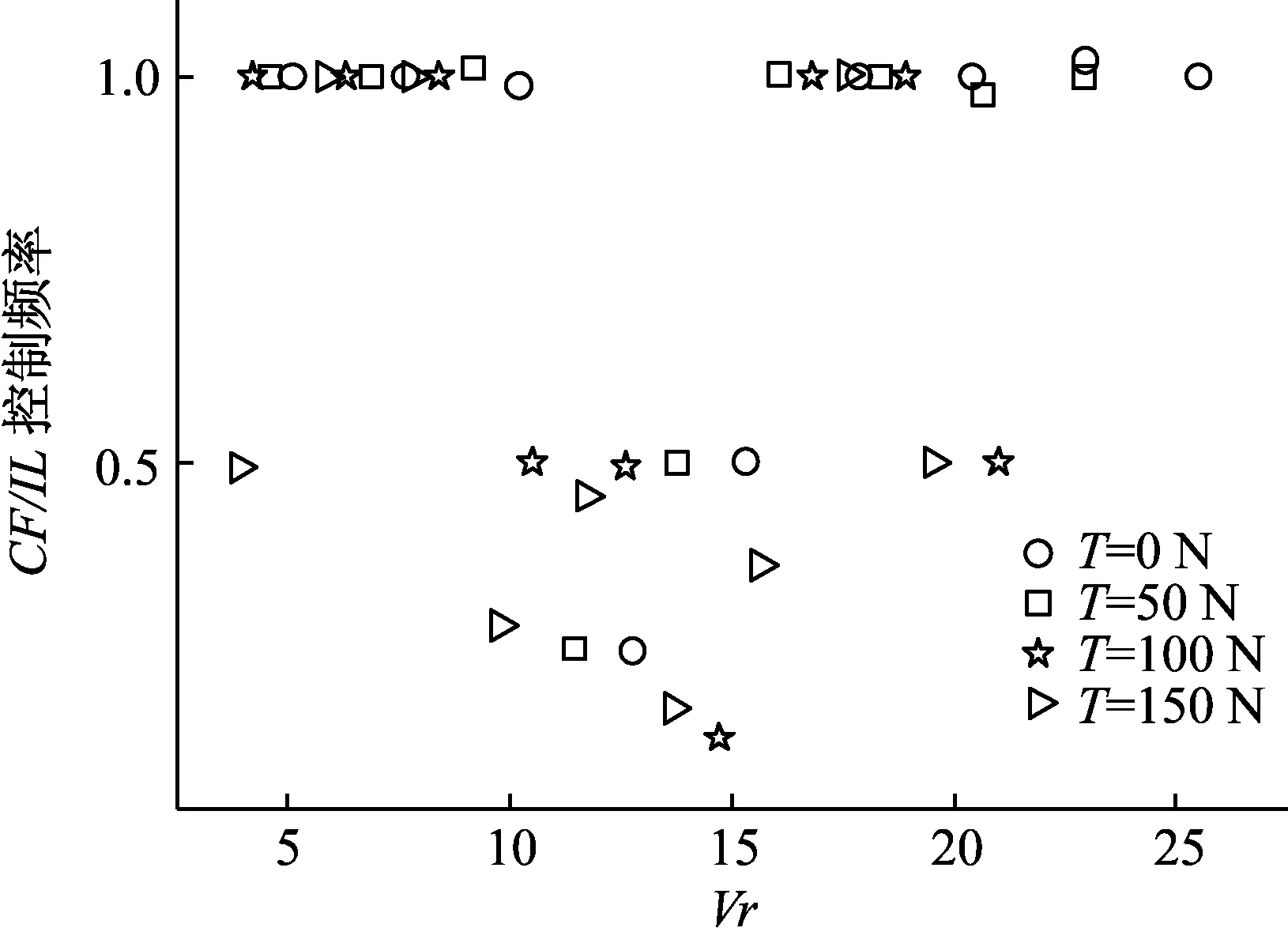



4 结 论
