面向微小卫星的类杆锥式软对接三维动力学建模与参数分析
2017-12-27黄奕勇
戚 杰, 张 翔, 赵 勇, 黄奕勇
(国防科技大学 航天科学与工程学院,长沙 410073)
面向微小卫星的类杆锥式软对接三维动力学建模与参数分析
戚 杰, 张 翔, 赵 勇, 黄奕勇
(国防科技大学 航天科学与工程学院,长沙 410073)
针对面向自主无人在轨服务的微小型航天器上使用的杆锥式对接机构,提出了一种在对接杆末端加缓冲系统的软对接方案。基于Lagrange方法建立了对接系统的三维动力学模型,并运用虚功原理求解广义力矩阵;接触点的确定采用接触搜索算法,提出了截面法,将三维空间搜索问题转化为二维平面求解;根据接触点的相对位置和速度关系,提出了三维空间中求解切向接触力的方法。 并且通过有限元方法与理论模型相比较,对理论模型进行了验证。通过对捕获锁的简化设计,制定了对接系统捕获的评判准则,并在不同的缓冲性能下进行动力学仿真分析,探讨缓冲参数变化对微小卫星对接过程的影响,提出了缓冲参数的优选方法,为锥杆式对接机构的缓冲系统设计提供有价值的参考。
杆锥式对接机构;三维动力学;Lagrange方法;接触搜索算法;截面法
自20世纪60年代首次实现空间交会对接以来[1],空间交会对接技术得到了迅猛发展,迄今为止,人类已成功进行了300多次的交会对接任务[2]。随着小型化、无人化空间飞行器的快速发展,针对面向微小卫星的自主对接机构逐渐引起了各国的关注。美国、意大利、日本相继开展了演示验证研究,主要项目包括美国密歇根宇航公司的AMDS[3-4]、意大利的ARCADE[5-6]、美国轨道快车对接捕获系统OECS[7-9]、日本的MS-DS 纳卫星对接系统[10-11]、哈工大类杆锥式对接机构[12]等项目。其中,意大利帕多瓦大学空间研究中心(CISAS)于2013年开发出微小卫星杆锥式对接实验系统(ARCADE),该系统是基于杆锥式的,主要采用弹性阻尼系统来缓冲接触过程中的接触力,并在平流层开展了空间微重力实验,该实验验证了对接实验系统的可行性和可靠性,但是在文献中没有深入的理论建模部分,也没有对弹簧阻尼器的缓冲性能进行理论分析;哈尔滨工业大学设计出的类杆锥式对接机构具有重量轻、可靠性高及对接范围大的优点,在完成缓冲、初始偏差补偿、捕获、姿态校正、刚性连接等对接任务的同时,能够提供较大对接平面,满足接口布局要求,容易建立电气、电液连接,适合在轨服务使用。本文主要面向微小卫星软对接需求,提出了一种带弹簧阻尼缓冲系统的杆锥式对接方案,并运用Lagrange方法与接触搜索算法建立系统的三维动力学模型。
Lagrange分析力学方法对研究系统动力学响应具有明显的优势,运用广义经典力学中的广义Lagrange 函数、广义坐标和广义力等概念,可以推导出力学系统的能量函数,为力学系统能量函数的推广和进一步应用提供了一种途径[13]。基于分析力学的Lagrange方法的已经在很多领域得到了研究[14],但在对接系统中研究较少。在接触问题的研究中,现在主要采用有限元方法[15],把实体结构(网格划分为二维单元或三维单元)相互接触的两个表面称为主表面(其上的节点称为主节点)和从表面(其上的节点称为从节点),在每一计算的时间步长内,检查从(主)节点是否穿越主(从)表面,如果没有穿越则对该节点不作处理;如有穿越,则对该节点与相应的表面进行处理。但是这样的搜索算法将耗费大量的时间[16],接触搜索占总计算时间的比例最高可达60%~80%[17],而且网格划分的方式对求解精度的影响十分显著。
本文主要面向微小卫星杆锥式对接过程,基于Lagrange分析力学理论,提出了一种带有缓冲装置的类杆锥式对接系统三维动力学建模方法。在接触碰撞过程中,根据杆锥式对接自身的特点,采用截面法,将三维搜索问题转化为二维平面问题进行求解,大大缩短搜索了时间。接着利用Hertz接触碰撞理论,确定法向碰撞力的大小和方向,同时,根据接触点的相对位置和速度关系,求解切向接触力的大小和方向。通过虚功原理,计算缓冲力、碰撞力的广义力矩阵,从而构建出对接系统动力学方程。模型的求解采用四阶Runge-Kutta法,在不同的对接条件和不同的模型参数下,进行仿真分析,探讨模型参数变化对微小卫星对接过程的影响情况。通过参数分析,提出了缓冲参数的优选方法。
1 基于Lagrange方法的三维动力学模型
1.1 问题描述
类杆锥式对接机构主要包括分别安装于主动和被动对接飞行器上的主动对接机构及被动对接机构两部分,对接过程分为捕获、缓冲校正、拉紧这几个阶段,其中捕获过程的动力学特性最为复杂,也是本文研究的重点。
为了改善对接机构的缓冲性能,在课题组原有地面样机的基础上,设计出新型的带缓冲装置的对接机构,如图1所示。主动对接机构由对接球头、缓冲阻尼器、对接杆筒、喷气气缸等部件组成,缓冲装置安装于对接球头末端。

图1 主动对接机构缓冲系统示意图Fig.1 Schematic diagram of buffer system of active docking mechanism
对接球头与滑动活塞相连,滑动活塞另一端与缓冲弹簧相连,当对接球头受到碰撞时,滑动活塞沿阻尼器内壁向后滑动,即可实现缓冲;与缓冲阻尼器相连的是对接杆筒,解锁顶针可沿其内壁滑动,当加注完成后,往喷气气缸里注入高压气体,接着在气压的作用下,解锁顶针向前滑动,直至顶针头部撞击捕获锁,实现解锁。
捕获锁的设计如图2所示,从图2(a)中可以看出,当对接球头到达捕获区域后,与凸轮捕获锁相碰撞,凸轮逆时针转动,推动滑块向后运动,在弹簧作用下,推动滑块运动到另一个卡口区域,实现锁紧,如图2(b)所示。

(a) 捕获前

(b) 捕获后图2 捕获锁工作原理示意图Fig.2 Schematic diagram of capture lock
为了方便建模,这里对对接机构进行了简化,如图3所示。缓冲装置简化为一自由度弹簧,捕获锁简化为捕获滑块。
当追踪星与目标星在一定的位置姿态偏差的条件下,追踪星以一定的初始速度相对于目标星沿主动对接方向运动。此时相对距离不断减小,对接球头开始与接纳锥发生碰撞,经缓冲后,球头沿着接纳锥内壁滑入捕获区域,与捕获滑块发生碰撞,当捕获滑块的行程达到一定数值后,则实现了对球头的捕获。
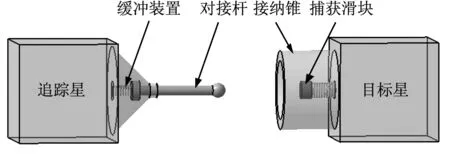
图3 对接机构简化示意图Fig.3 Schematic diagram of docking mechanism
1.2 三维动力学建模
1.2.1 模型假设
为研究方便且不失一般性,首先需要对整个对接系统进行适当简化。
(1) 在对接过程中主动航天器、被动航天器、主动对接机构和被动接纳锥的小变形忽略不计,视为刚体,主要考虑缓冲装置的变形;
(2) 对接捕获过程中接触碰撞为点——点接触碰撞;
(3) 主动对接机构和主动航天器之间由一组缓冲阻尼器相连,主动对接机构可以相对于主动航天器沿轴向运动,不考虑缓冲系统的质量惯量特性,仅考虑其弹性阻尼特性;
(4) 捕获锁简化为捕获滑块,捕获滑块通过弹簧与目标星连接,可以沿目标星轴向运动,主动对接机构通过撞击捕获滑块,实现捕获;
(5) 主动航天器和被动航天器在空间环境下均可实现六自由度运动。简化后得到机构动力学关系如图4所示。
1.2.2 坐标系的建立以及广义坐标的选取
空间对接过程涉及到追踪星、目标星以及主动对接机构之间的相对运动,为描述它们之间的相对位置和姿态信息,需定义合适的坐标系。坐标系的定义如图4所示。
在追踪星上建立体坐标系b1,原点O1选在追踪星的质心上,X1轴指向主动对接方向,Y1轴和Z1轴分别构成右手系。在目标星上建立体坐标系b2,原点O2选在目标星的质心上,X2轴指向主动对接方向,Y2轴和Z2轴分别构成右手系。
惯性坐标系到体坐标系的向量变换按照321的转序进行,俯仰角为Ψ,偏航角为θ,自旋角为φ。

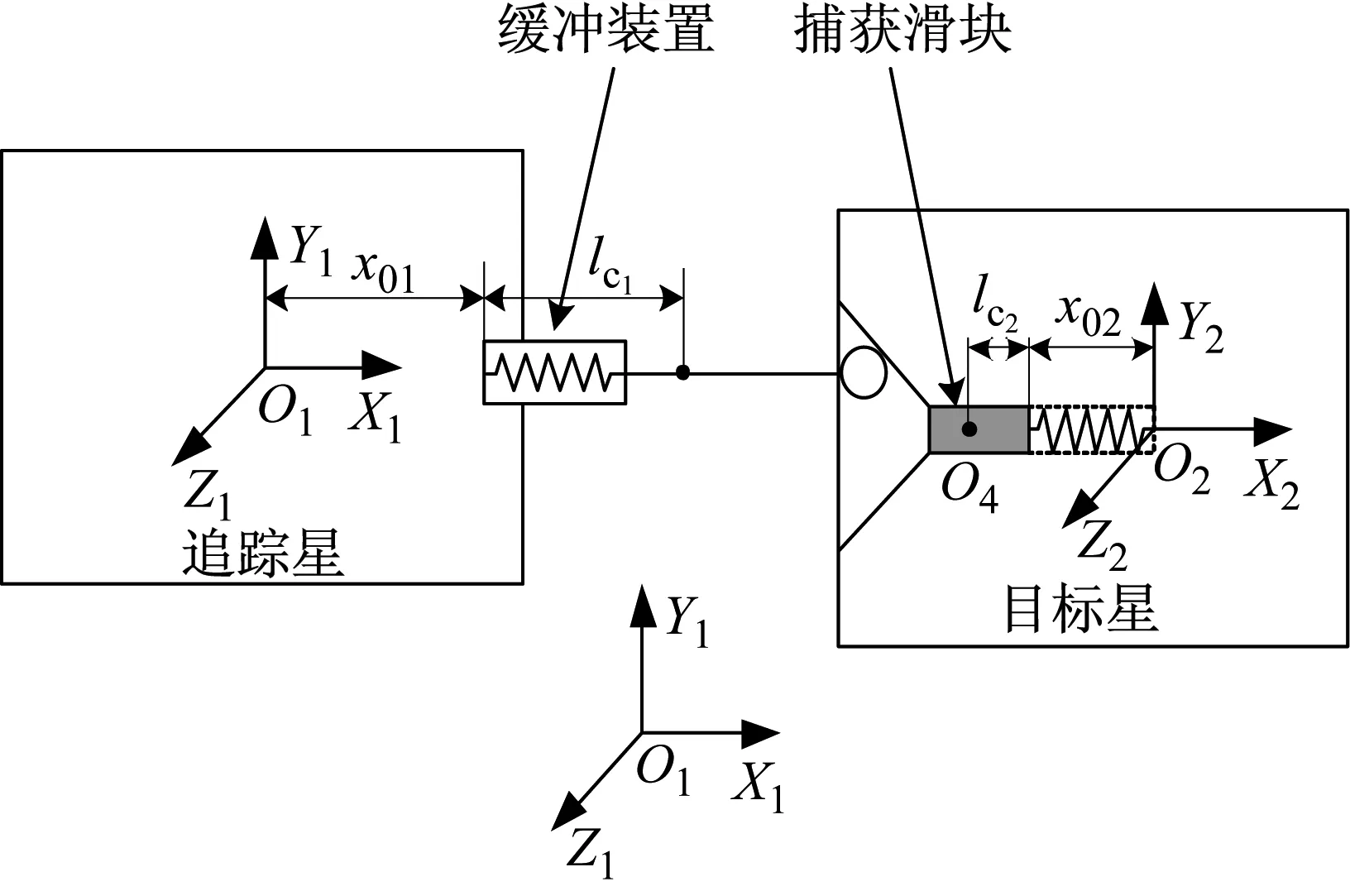
图4 对接系统示意图Fig.4 Schematic diagram of docking system
1.2.3 系统动能
根据刚体的动能公式,刚体的动能等于刚体质心的平动动能与绕质心的转动动能之和。所以系统动能的矢量表达式为
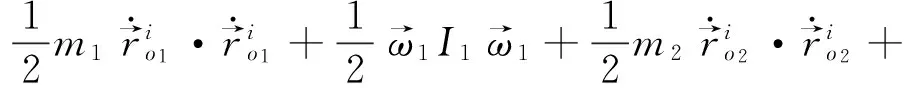
(1)
根据矢量关系:
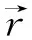
(2)
(3)
所以:
(4)
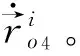
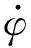


(5)
将式(4)、(5)代入式(1)得系统动能的广义坐标表达式:
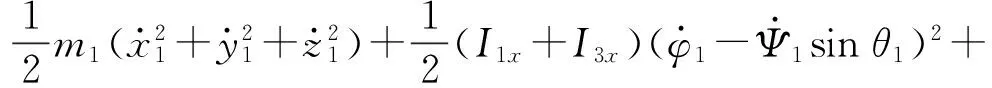
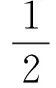
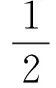
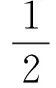
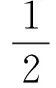
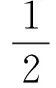
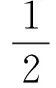

(6)
式中:x02为被动航天器质心到捕获滑块末端的长度,lc2为捕获滑块质心的位置。各部分参数如图4所示。
1.2.4 系统动力学方程
根据Lagrange方程[18]:

(7)
式中:qi为各个自由度;Qqi为各个自由度方向上的广义力。
将式(6)代入式(7),那么杆锥式对接机构三维动力学方程为
(8)
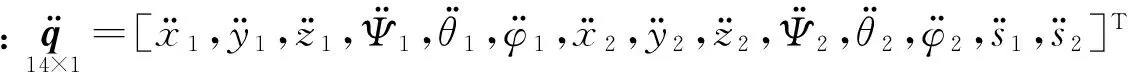
M和D见附录
1.3 广义力矩阵求解
1.3.1 缓冲力的广义力矩阵
根据虚构原理,缓冲力的虚功为

(9)
式中:k1,c1分别为缓冲装置的刚度系数和阻尼系数;k2,c2分别为捕获滑块的刚度系数和阻尼系数。
所以缓冲力的广义力为
Qh=[0,0,0,0,0,0,0,0,0,0,0,0,

(10)
1.3.2 接触力的广义力矩阵
(1)法向接触力的广义力矩阵
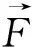

图5 法向接触力示意图Fig.5 Schematic diagram of normal contact force δW法向接触力=Nδ球头-Nδ锥点=
(11)


(12)
转化为惯性系下有:
(13)
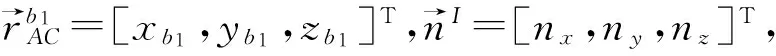
(14)

(15)
(2)切向接触力的广义力矩阵
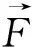

(16)
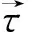
2 接触算法
2.1 接触点确定
在捕获过程中,对接球头与接纳锥内壁发生接触,由于球头和接纳锥均在三维空间中运动,在三维空间搜索接触点是比较困难的。本文采用截面法,把空间接触点搜索问题转化到二维平面进行求解。
对于球头来说,球面上任意一点均可以由过球心的平面截得;对与接纳锥来说,锥为回转体,锥内壁面上的任意一点均可以由过回转轴线的平面截得。当球头与接纳锥内壁发生碰撞时,球面上的接触点与锥内壁面上的接触点重合,那么这个碰撞点可以由球心与回转轴线所确定的平面截得。根据Herz接触碰撞理论,球头与接纳锥发生碰撞时,将发生相互侵入,已知某一时刻,该截面所显示的相对位置关系,如图6所示。


图6 碰撞点截面示意图Fig.6 Schematic diagram of section of collision point
此时球头上的碰撞点是点C,接纳锥上的碰撞点是点B,以b2坐标系为计算坐标系,已知对接球头球心坐标A=[xA,yA,zA]T,球头半径为R,锥角为α,目标星质心到接纳锥顶点的距离为l2。又有截面过球心,所以截得的圆为球的大圆,圆点为A,把BA延长至与回转轴相交于点Q,过点A作回转轴的垂线,与回转轴交于点P,与接纳锥内壁相交于点A′,那么根据几何位置关系:
P=[xA,0,0]T
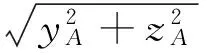
求出点C的坐标后,即可判断C点有无侵入。

那么,
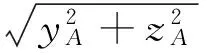
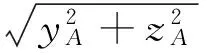
如果C点有侵入,那么侵入深度
那么此时球头和接纳锥上的碰撞点分别为
2.2 接触力的求解
2.2.1 法向接触力求解


(17)

(18)

图7 弹簧阻尼模型示意图Fig.7 Schematic diagram of spring-damper model
当δ≥0时,对接球头与对接锥面之间处于接触碰撞阶段,其法向接触力FN为
FN=Fk+Fd
(19)
式中:Fk为接触过程中的弹簧恢复力;Fd为接触过程中的阻尼力。
弹簧恢复力Fk由Hertz接触理论[19]确定:
(20)
式中:K为接触刚度;K值一般与接触体的几何形状和材料有关:


应用Hertz模型对本套机构接触碰撞力进行计算,模型中考虑了碰撞过程中存在能量消耗,并认为能量损耗由材料阻尼引起,那么基于Hunt Crossley[20]阻尼模型,阻尼力的计算公式为
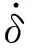
(21)

碰撞力的方向与过接触点的法线向量方向一致:
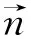
(22)
2.2.2 切向接触力求解
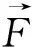
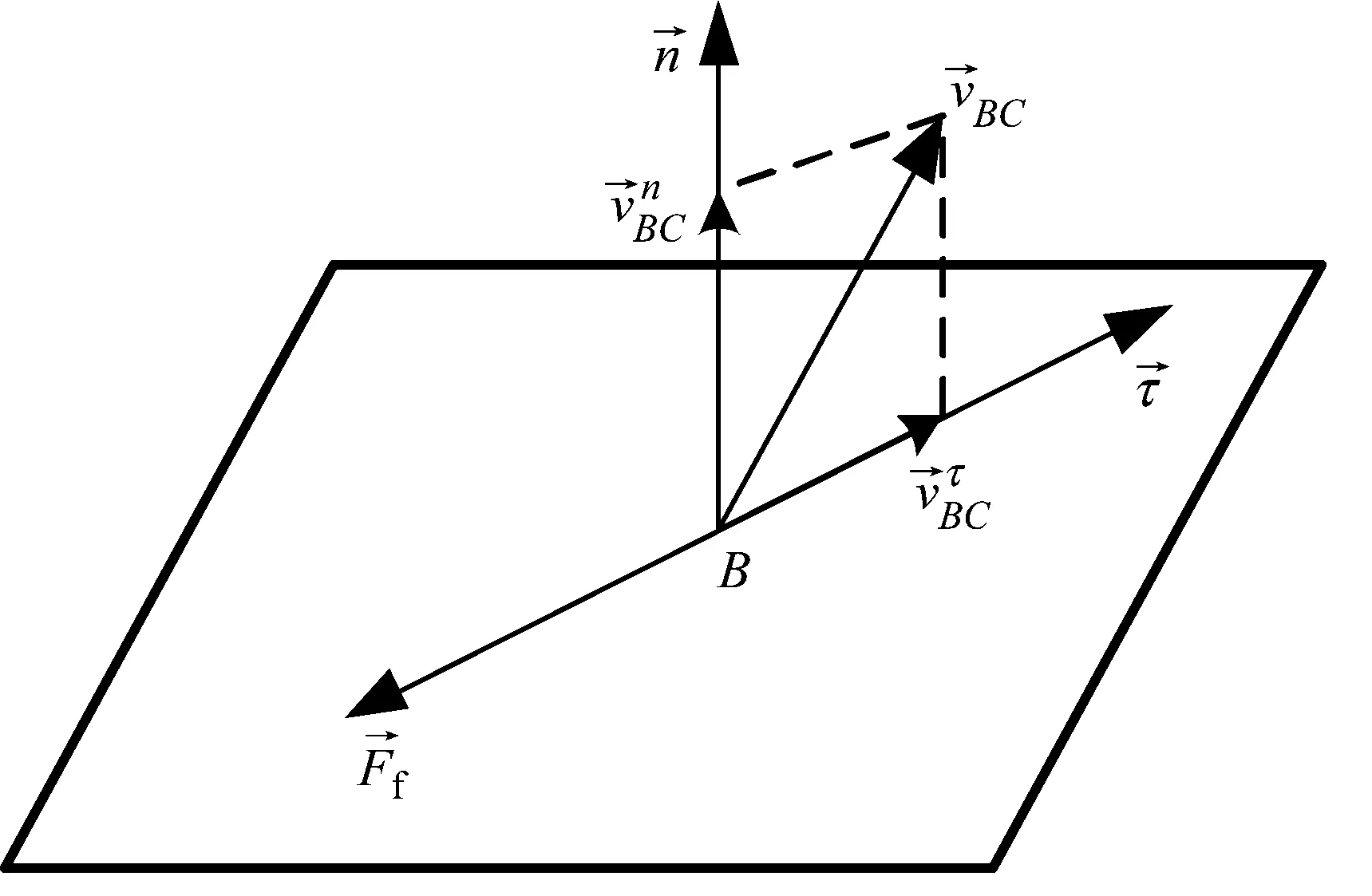
图8 切向接触力方向示意图Fig.8 Schematic diagram of direction of tangential contact force

(23)

3 模型求解与分析
3.1 模型参数
对接杆和接纳锥的基本几何参数设计如表1所示。
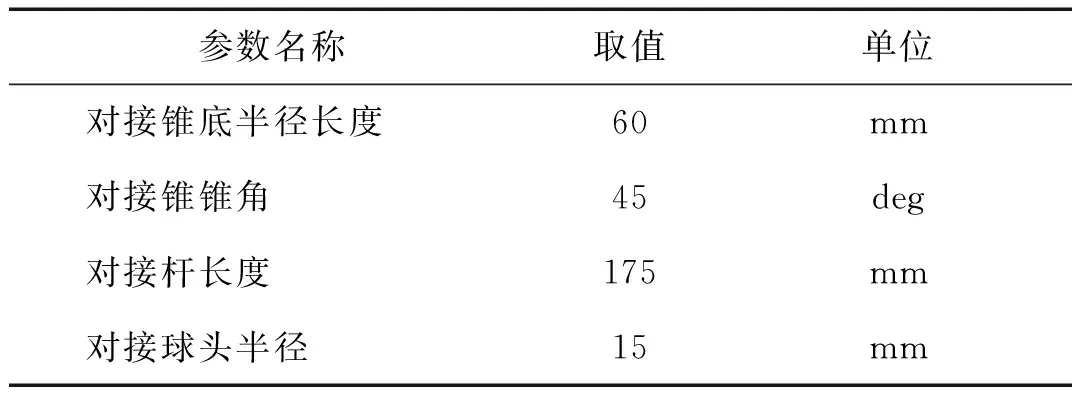
表1 对接杆和接纳锥的基本几何参数表Tab.1 The basic geometric parameters table ofDocking probe and Receiving cone
对接机构质量属性如表2所示。

表2 对接机构质量属性表Tab.2 The quality attribute table of Docking mechanism
3.2 模型验证
本文为了验证上述所建三维模型的正确性,采用有限元方法对理论模型进行验证,通过有限元商业软件ABAQUS,对对接捕获过程进行模拟。两星的轴向偏差为0.04 m,初速度为0.1 m/s,相对姿态角和姿态角速度均为0,在缓冲参数K1=1×105N/m,C1=1×103N·s/m的情况下,对接触力、质心速度、缓冲装置行程和捕获距离的时间历程曲线进行比对。
图9中,(a)为接触力时间历程曲线,接触过程是一个极为复杂的过程,在接触力的求解过程中,理论模型和有限元方法运用的求解方法不一样,所以导致接触力不能完全匹配得上,但是二者所求得的接触力的趋势是相近的,从而证明了理论模型的合理性。

(a) 接触力

(b) X轴向速度

(c) 缓冲弹簧行程

(d) 捕获距离图9 理论模型与有限元方法对比图Fig.9 Theoretical Model and Finite Element Method comparison chart
图9(b)、(c)、(d)分别为质心速度(X方向)、缓冲装置行程和球心距捕获中心距离的时间历程曲线,在图中可以看出,在1.38 s时刻发生碰撞,导致了对接系统的运动状态发生改变。理论模型所计算的曲线和有限元方法计算的曲线吻合得比较好,充分显示了理论模型的合理性。
3.3 结果与分析
为了研究缓冲参数对对接系统捕获性能的影响,本文主要对缓冲系统的刚度系数进行分析。表3为对接系统的初始条件。

表3 对接初始条件表Tab.3 The docking initial condition table
捕获成功的评价准则为:
(1)对接球头进入捕获区域,球心与捕获中心在主动对接方向上的距离小于等于0。
(2)对接球头撞击捕获锁,使得捕获锁的行程大于5 mm。
表4给出了不同的刚度系数,在阻尼值C1=100 N·s/m的条件下进行仿真分析。
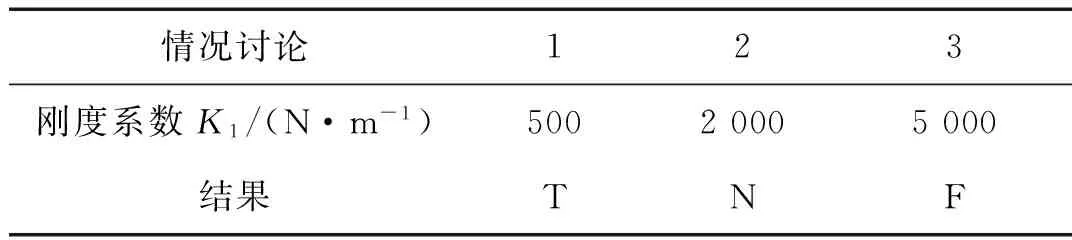
表4 刚度系数表Tab.4 The stiffness coefficient table
结果中,T表示对接球头与捕获锁发生碰撞,并且撞开捕获锁顺利进入捕获区域;N表示对接球头与捕获锁发生了接触,但是没能撞开捕获锁;F表示对接球头没有与捕获锁接触,捕获失败。通过采用表3种不同的刚度系数,求解出杆和锥首次碰撞的碰撞力时间历程曲线,如图10所示。
根据图10碰撞力时间历程曲线可以看出,一次碰撞由许多小的碰撞峰值组成,每次小的碰撞持续的时间很短,在毫秒量级。在不同的刚度系数下,除第一个峰值的值比较接近以外,其余的峰值则表明,刚度越小,碰撞力越小,这说明缓冲装置的缓冲效果是显著的。当K1=500时,可以实现成功捕获,较大的刚度系数使得机构得不到足够的缓冲而使捕获失败。

图10 接触力时间历程曲线Fig.10 Time history curve of contact force
图11反映了球心距捕获中心距离随时间变化的曲线,当K1=500时,在T=0.6 s时刻,距离达到最小值0,实现了成功捕获。当K1=2 000和K1=5 000时,最小距离均大于0,并在该距离后逐渐增大,这表明球头距捕获中心越来越远,捕获失败。

图11 球心距捕获中心的距离(沿主动对接方向)时间历程曲线
Fig.11 Time history curve of the distance of globe center from the center of captureing(along the direction of the active docking)
图12给出了追踪星和目标星质心速度随时间变化的曲线,对接过程中,对接杆和接纳锥每次接触时,追踪星质心沿主动对接方向速度逐渐减小,目标星质心沿主动对接方向速度逐渐增大;每次接触结束后,追踪星和目标星质心沿主动对接方向的速度保持恒定。当K1=500时,在T=0.6 s时刻实现捕获,此时追踪星质心速度大于目标星质心速度,两星不断靠近;当K1=2 000和K1=5 000时,两星质心速度呈交替变化后,目标星质心速度大于追踪星质心速度,两星呈不断分离,捕获失败。

图12 质心速度(沿主动对接方向)时间历程曲线
Fig.12 Time history curve of centroid speed(along the direction of the active docking)
4 结 论
(1) 本文以面向微小卫星在轨服务的杆锥式对接机构设计为背景,提出了一种在对接杆末端加轴向缓冲装置的软对接方案,并将捕获滑块引入到对接系统中,把捕获滑块的行程作为判断捕获成败的准则之一。基于Lagrange分析力学方法,建立了系统的三维动力学模型,并根据虚功原理,确定缓冲力、法向接触力、切向接触力的广义力矩阵;在接触搜索算法中,通过截面法将接触点的搜索范围从三维空间减小到二维平面,大大提高的搜索效率;运用Hertz接触理论,对法向接触力进行求解;根据接触点的相对位置和相对运动关系,提出了切向接触力的求解方法。
(2) 运用有限元商用软件(ABAQUS)建立了对接系统的有限元模型,通过计算对接过程中的接触力、X轴向速度、缓冲弹簧行程以及捕获距离的时间历程曲线,与理论模型作对比,验证了理论模型的正确性。
(3) 对缓冲系统的刚度系数进行了分析,提出了缓冲参数的优选方法。通过选取不同的刚度值,对接触力、球心距捕获中心的距离、质心速度进行了分析。结果表明,缓冲系统对对接系统动力学特性的影响十分显著,合适的弹簧刚度系数的选取能有效提升对接系统的捕获能力。
[1] 陈小前,袁建平,姚雯,等. 航天器在轨服务技术[M]. 北京: 中国宇航出版社, 2009.
[2] 陈宝东, 唐平. 空间对接机构技术及其研制[J]. 上海航天, 2005(5):6-8.
CHEN Baodong,TANG Ping.The technology and develop of space docking mechanism[J]. Shanghai Aerospace, 2005(5):6-8.
[3] HAYS A B, TCHORYK JR P, PAVLICH J C, et al. Dynamic simulation and validation of a satellite docking system[C]. Aero Sense, 2003: 77
[4] RIVERA D E, MOTAGHEDI P, HAYS A. Modeling and simulation of the MichiganAerospace autonomous satellite docking system II[C]. Defense and Security, 2005: 82
[5] BOESSO A, FRANCESCONI A F. ARCAD small-scaledocking mechanism for micro-satellites[J]. Acta Astronautica. 2013:77-87.
[6] BARBETTA M, BOESSO A, BRANZ F, et al. ARCADE-R2 experiment on board BEXUS 17 stratospheric balloon[J]. CEAS Space Journal, 2015, 7(3):347-358.
[7] MOTAGHEDI P. On-orbit performance of the orbital express capture system[C]. SPIE Defense and Security Symposium. 2008:
[8] CHRISTIANSEN S, NILSON T. Docking System for autonomous, un-manned docking operations[C]. IEEE Aerospace Conference, 2008.
[9] 林来兴. 美国“轨道快车”计划中的自主空间交会对接技术[J]. 国际太空,2005(2):23-27.
LIN Laixing.The autonomous space rendezvous and docking technology of American "Orbital Express" program[J]. Space International,2005(2):23-27.
[10] SATORI S. Status of nanosatellite development for mothership-daughtership space experiment by japanese university[C]. Proceedings of the 22nd ISTS,Morioka, May, 2000:2323.
[11] UI K, MATUNAGA S. Identification of docking possibility criteria including recovery from incomplete grasping of docking mechanism for nanosatellite[J]. Journal of Space Engineering, 2009, 2(1):1-11.
[12] 张大伟,田浩,赵阳,等.类杆锥式对接机构捕获动力学分析与参数设计[J].宇航学报,2008,29(6): 1717-1722.
ZHANG Dawei,TIAN Hao,ZHAO Yang,et al. Quasi probe-cone docking mechanism capturing dynamics analyses and parameter design[J]. Journal of Ast Ronautics, 2008, 29(6): 1717-1722.
[13] SANTILLI R M.Foundations of theoretical mechanics:theinverse problem in Newtonian mechanics[M].California:Springer-Verlag Press,1978:110-160.
[14] 殷婷,王杰. Lagrange 力学化理论在多机电力系统中的应用[J]. 电网技术,2013,37(9):2486-2491.
YIN Ting, WANG Jie.Application of lagrange mechanization theory in multi-machine power system[J]. Power System Technology,2013,37(9):2486-2491.
[15] HALLQUIST J O,GOUDREAU G L,BENSON D J. Sliding interfaces with contact-impact in large-scale lagrangian computations[J]. Computer Methods in Applied Mechanics and Engineering,1985,51(1):107-137.
[16] SCHWEIZERHOF K, NILSSON L, HALLQUIST J O. Crachworthiness analysis in the automotive industry[J].International Journal of Computer Applications in Technology, 1992, 5(2/3/4):134-156
[17] BENSON D J, HALLQUIST J O. A single surface contact algorithm for the post-buckling analysis of shell structures[J].Computer Methods and Applied Mechanics, 1990, 78:141-150
[18] 孙世贤,黄圳圭,唐乾刚. 理论力学[M]. 长沙:国防科技大学出版社,2008.
[19] 张翔. 基于空间杆-锥式对接机构的柔性杆技术研究[D].长沙: 国防科技大学,2011.
[20] 马易志.柔性多体系统接触碰撞的理论和实验研究[D]. 上海:上海交通大学,2008.
Three-dimensionaldynamicmodelingandparametricanalysisforquasiprobe-conesoftdockingusedinminiaturesatellites
QI Jie, ZHANG Xiang, ZHAO Yong, HUANG Yiyong
(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Aiming at probe-cone docking mechanisms used in miniature spacecrafts for unmanned autonomous on-orbit service, a soft docking scheme of adding a buffer system at the end of the rod butt was proposed. A three-dimensional dynamic model for the docking system was built based on Lagrange method, the principle of virtual work was used to solve the generalized force matrix. The contact search algorithm was utilized to determine contact point positions, the section method was employed to convert a three-dimensional space search problem into a two-dimensional planar solution. According to relative position and relative speed of contact points, a method was proposed to solve a tangential contact force in a three-dimensional space. Moreover, the theoretical model was verified through comparing the results of the finite element method with those of this model. Assessment criteria of docking system capture were established through the simplified design of capture lock. Dynamic simulation analyses were performed under different cushioning characteristics. The influence of changes of buffer parameters on docking process of micro-satellites was analyzed, the optimization method for buffer parameters was proposed to provide a valuable reference for the buffer system design of a probe-cone docking mechanism.
probe-cone docking mechanism; three-dimensional dynamics; Lagrange method; contact search algorithm; section method
国家自然科学基金(91216201;51205403;11404405)
2016-05-26 修改稿收到日期:2016-09-05
戚杰 男,硕士生,1992年生
赵勇 男,博士,教授,硕士生导师,1977年生
TH113
A
10.13465/j.cnki.jvs.2017.23.010
