不同粗糙度斜拉索气动力特性和风荷载计算方法研究
2017-12-27刘庆宽闫煦东李聪辉郑云飞马文勇刘小兵
刘庆宽, 闫煦东, 李聪辉, 郑云飞, 马文勇, 刘小兵
(1. 石家庄铁道大学 大型结构健康诊断与控制研究所,石家庄 050043;2. 河北省大型结构健康诊断与控制重点实验室,石家庄 050043; 3. 石家庄铁道大学 土木工程学院,石家庄 050043)
不同粗糙度斜拉索气动力特性和风荷载计算方法研究
刘庆宽1, 2, 闫煦东3, 李聪辉3, 郑云飞3, 马文勇1, 2, 刘小兵1, 2
(1. 石家庄铁道大学 大型结构健康诊断与控制研究所,石家庄 050043;2. 河北省大型结构健康诊断与控制重点实验室,石家庄 050043; 3. 石家庄铁道大学 土木工程学院,石家庄 050043)
大跨径斜拉桥斜拉索上的风荷载对主梁的位移和内力的贡献占全桥的主要部分,准确掌握斜拉索上的风荷载,对于桥梁的抗风设计具有重要的意义。通过风洞试验,得到了8种具有不同表面粗糙度斜拉索的气动力系数随雷诺数的变化规律,研究了粗糙度对斜拉索雷诺数效应和气动力特性的影响,以实桥为例分析了斜拉索最大风荷载的计算方法。结果表明:斜拉索表面的粗糙度对气动力具有明显的影响,随着粗糙度的增大,雷诺数效应随之减弱;不同粗糙度的斜拉索,最大风荷载对应的风速不同,计算方法也不同,实桥设计时应根据斜拉索的具体表面粗糙状态确定其最大风荷载的数值。
斜拉索;气动力;粗糙度;雷诺数效应;最大风荷载
对于大跨径斜拉桥来说,两方面的因素使得桥梁的设计风速较高:一是桥梁自身的结构特点,为了通航的要求,主梁和斜拉索离水面较高;二是所处的风环境特征,大部分大跨度桥梁在东南沿海基本风速比较大的区域建设。较大的设计风速使得桥梁的风荷载和风致振动经常成为结构设计的关键因素。以苏通长江公路大桥为例,研究显示:在横桥向风的作用下,斜拉索产生的风荷载对于主梁位移和内力的贡献占全桥风荷载的60%~70%[1]。因此,准确掌握斜拉索上的风荷载,对于内力和稳定计算以及振动验算等,具有重要意义。
目前的斜拉索表面材料大部分为热挤聚乙烯,除去附加抑振风雨振的螺旋线或者凹坑之外,出厂时均为光滑的表面,粗糙度指数很低;然而随着在桥上服役期的延长,斜拉索表面受到环境的影响,如风吹日晒、空气中漂浮物的粘附等,表面粗糙度会逐渐变大,甚至出现裂缝等[2]。斜拉索表面粗糙度的增大会导致临界雷诺数减小,在相对较小风速下产生较大的横向力,进而可能激发起斜拉索的大幅振动。这也可能是斜拉索产生大幅振动的诱因之一[3-4]。
进行风荷载计算时,对于具有圆形断面的斜拉索,雷诺数效应是需要考虑的问题。在亚临界雷诺数区域,阻力系数基本不随雷诺数的变化而改变;在临界雷诺数区,阻力系数随着雷诺数的增大而减小[5]。对于同一个斜拉索和相同的空气条件,风速同雷诺数成正比,因此在临界雷诺数区域,阻力系数随着风速的增大而减小,根据阻力的计算公式(FD=0.5ρV2CDA,其中FD、ρ、V2、CD、A分别是单位长度斜拉索的阻力、空气密度、风速、阻力系数和单位长度受风投影面积)可知:阻力与风速的平方和阻力系数成正比,临界雷诺数区风速增大的同时阻力系数减小,使得阻力不一定随着风速的增大而单调增大,最大风速对应的阻力,不一定是整个风速范围内的最大阻力。另外,现在有关斜拉索风荷载计算的规范,欧洲、日本规范与我国的JTG/T D60-01—2004《公路桥梁抗风设计规范》[6-7](以下简称《规范》)均只考虑了阻力,没有考虑升力。国内外的学者研究成果也多集中在斜拉索阻力系数的研究[8-10],关于升力对斜拉索风荷载的贡献缺乏必要的研究。
从圆柱结构周围的流场变化分析,在亚临界和超临界雷诺数区,流场在时间平均上基本是对称的,表现在平均升力上其数值接近0,在这两个区间不考虑升力是没有问题的。但是雷诺数进入临界区域时,周围流场变得不再对称[11],不对称流场会产生平均升力,并可能导致斜拉索的振动[12-13]。因此,研究掌握临界区的平均升力大小对斜拉索风荷载的贡献,以及进行风致振动分析是有意义的。
本文通过风洞试验,对不同粗糙度表面的斜拉索的阻力和升力进行了测试,得到了阻力系数和升力系数随雷诺数的变化规律,并以苏通长江公路大桥为例,用《桥规》的计算方法和本文的计算方法进行了气动力的计算比较和讨论。需要说明的是,本文中的气动力和气动力系数均指平均气动力和平均气动力系数,以区别脉动力和脉动力系数。
1 风洞试验
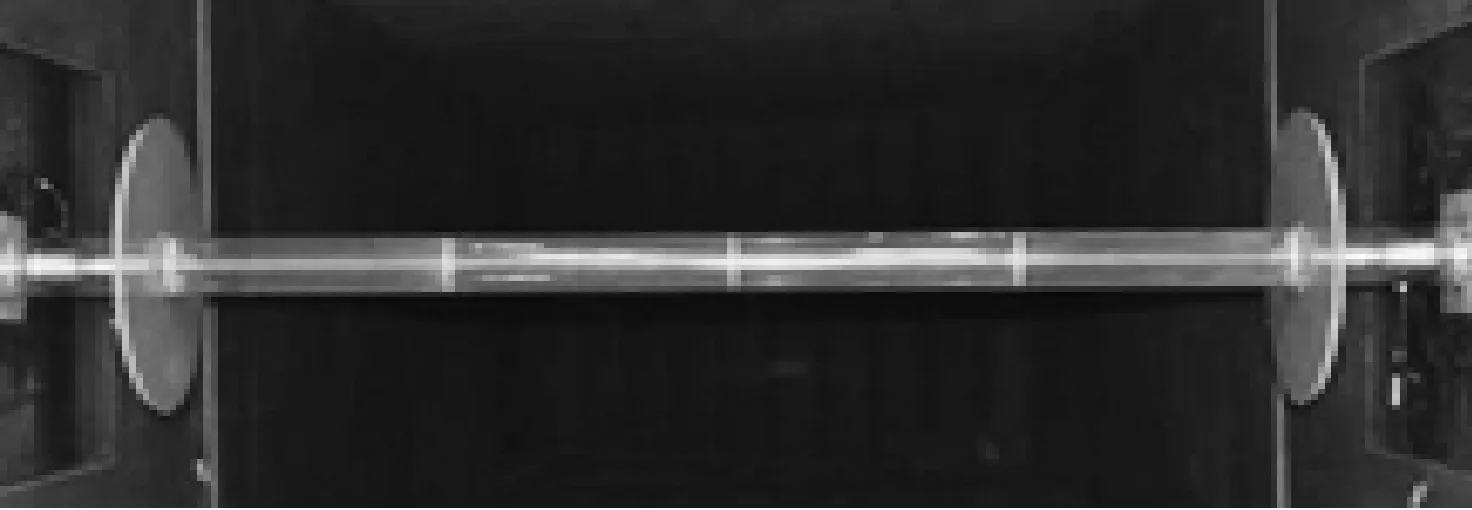
本研究的风洞试验在石家庄铁道大学风工程研究中心的STU-1风洞的高速试验段进行。试验段宽2.2 m,高2.0 m,长5.0 m,最大风速80 m/s。斜拉索模型为直径约120 mm的刚性有机玻璃管制成,中间贯穿具有足够刚度的钢管,固定在两端的高频测力天平上。模型区在40 m/s和65 m/s时的湍流度不大于0.16%。在模型表面包裹不同型号的工业砂纸以得到不同的表面粗糙度。将光滑的没有包裹砂纸的模型作为M1,按照粗糙度从小到大7个包裹工业砂纸的模型分别作为M2~M8,8个试验模型的细部照片见图1(为了对比,照片中放置了钢尺),在风洞中模型整体照片见图2。

M1

M2

M3

M4

M5

M6

M7

M8图1 模型表面状态Fig.1 Model surface
每个斜拉索模型分别在模型两端、中间、1/4和3/4处等五个断面、每个断面的四个方向,利用游标卡尺测试其直径,得到平均直径,作为计算气动力系数的模型直径值。多处测试直径的目的除了获得准确的直径数值之外,也是为了保证模型圆度的均匀性,避免某个方向的明显偏差引起气动力的变化。测试结果表明模型直径在各个位置基本均衡分布。
模型表面粗糙度测试采用日本MITUTOYO公司生产的SJ-411表面粗糙度仪测试。该设备分辨率为0.01 μm,最大取样长度25 mm。
粗糙度指标依据国标《产品几何级数规范(GPS)表面结构轮廓法术语、定义及表面结构参数》[14]定义,各个模型的直径和粗糙度见表1。
其中:Pa为评定轮廓的算术平均偏差,其表达式为:
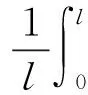
M1

M2

M3

M4

M5

M6

M7

M8图2 模型在风洞内的照片Fig.2 Model in wind tunnel
Pq为评定轮廓的均方根偏差,其表达式为
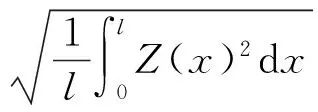
Pz为轮廓最大高度,为最大的轮廓高和最深谷深之和。
其中取样长度l和偏差Z(x)见图3。

图3 粗糙度取样长度和偏差Fig.3 Sampling length and deviation of roughness
模型的安装如图4所示。模型受力部分的长度为1 700 mm,两端分别安装了补偿模型,并安装了5倍斜拉索模型直径的端板。通过补偿模型避开了风洞两侧的洞壁形成的边界层,保证受力部分处于均匀的流场中;通过端板保证了模型受力部分流场的二维流动,有效消除的模型的端部效应。

表1 斜拉索模型的参数Tab.1 Parameters of cable models

图4 模型安装示意图Fig.4 Cable model installation
斜拉索模型气动力由两端安装的美国ATI公司生产的DELTA系六分量高频天平测试。模型阻力和升力方向上的量程为330 N,满量程精度为1/16 N, 频率为1 500 Hz。
风速由澳大利亚TFI公司生产的Cobra Probe测试。风速测量范围为2~65 m/s, 风速测量精度为±0.5 m/s, 响应频率为2 000 Hz。
试验模型的雷诺数通过式(1)进行计算。

(1)
式中:U为来流风速(m/s);D为斜拉索模型直径(m);ρ为空气的密度(kg/m3);μ为空气动力粘性系数;ν为空气运动黏性系数。试验中记录风洞洞体内的温度、湿度和大气压,计算得到空气的运动粘性系数ν,并计算得到雷诺数的数值。
为了准确获得临界雷诺数区气动力的变化情况,在亚临界、临界和超临界雷诺数区分别利用不同的风速步长进行测试,其中临界雷诺数区的步长较小。各个模型的试验雷诺数步长如表2所示。

表2 试验雷诺数步长Tab.2 Step of test Reynolds number
2 粗糙度对斜拉索气动力的影响
前人的研究发现:斜拉索的气动力主要和斜拉索表面粗糙度、流场的湍流度和模型的长细比等因素有关[15]。本研究主要针对粗糙度对斜拉索气动力的影响。
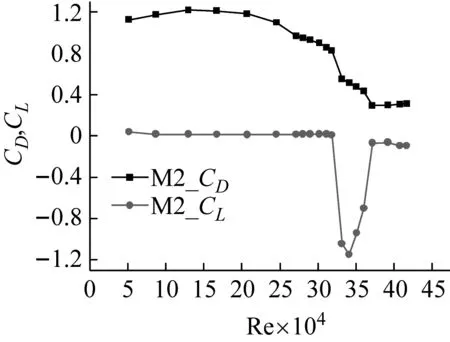
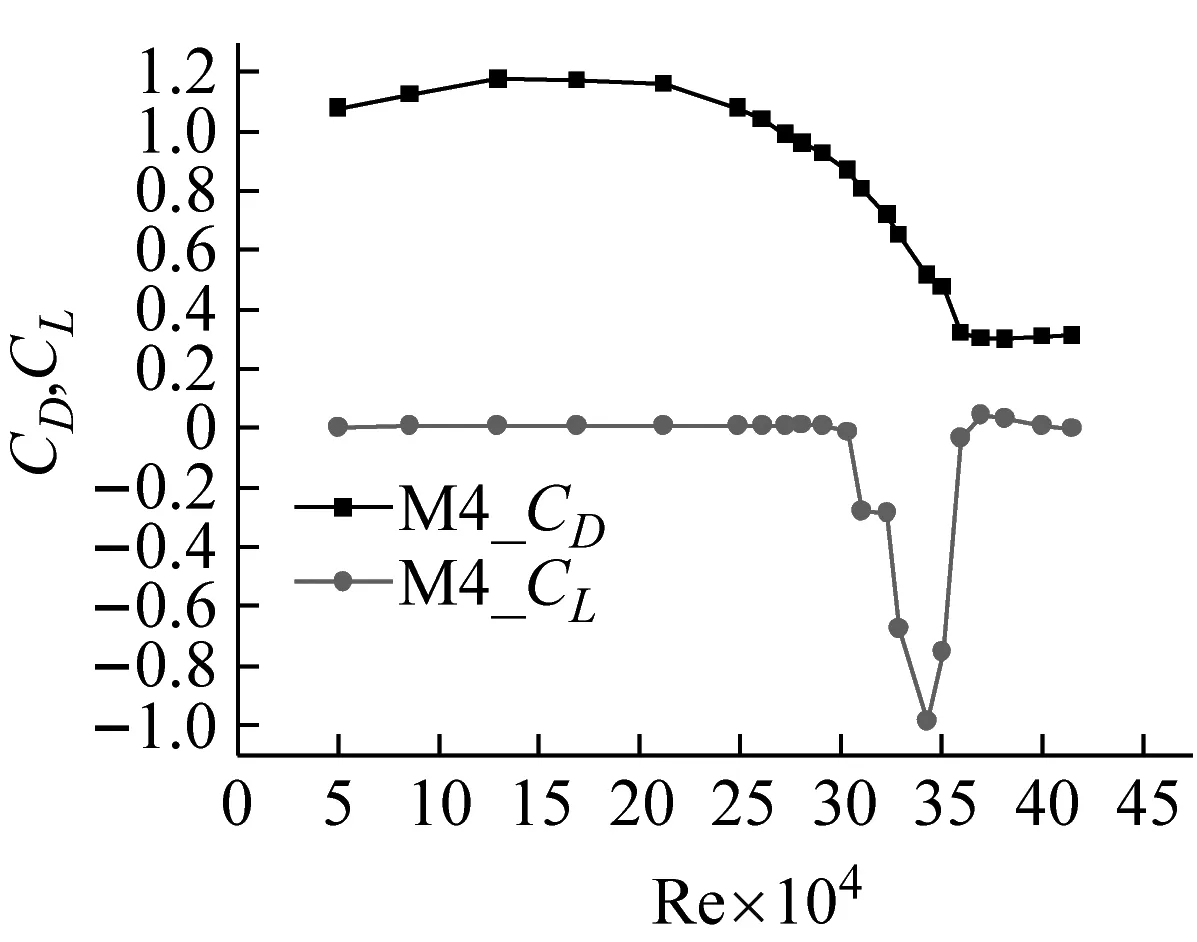
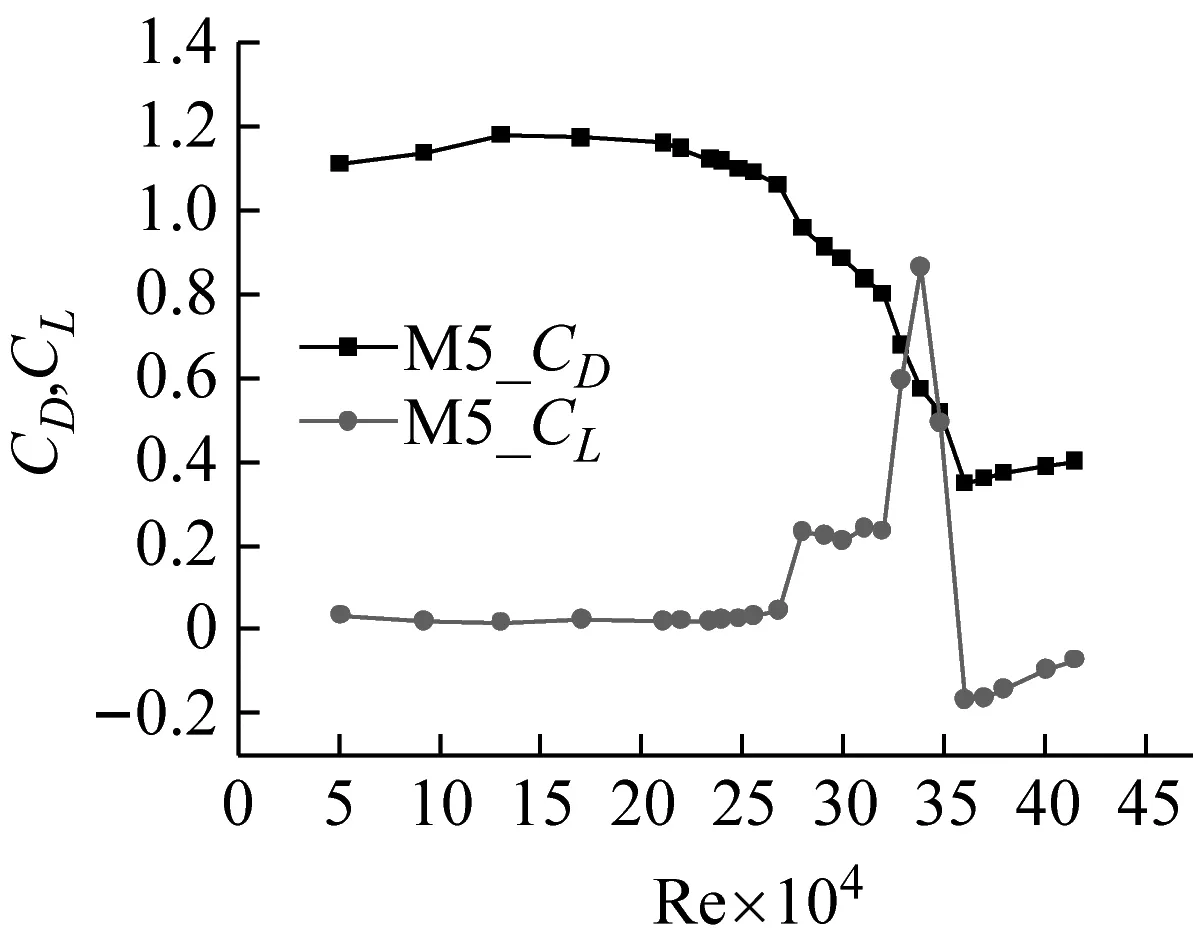
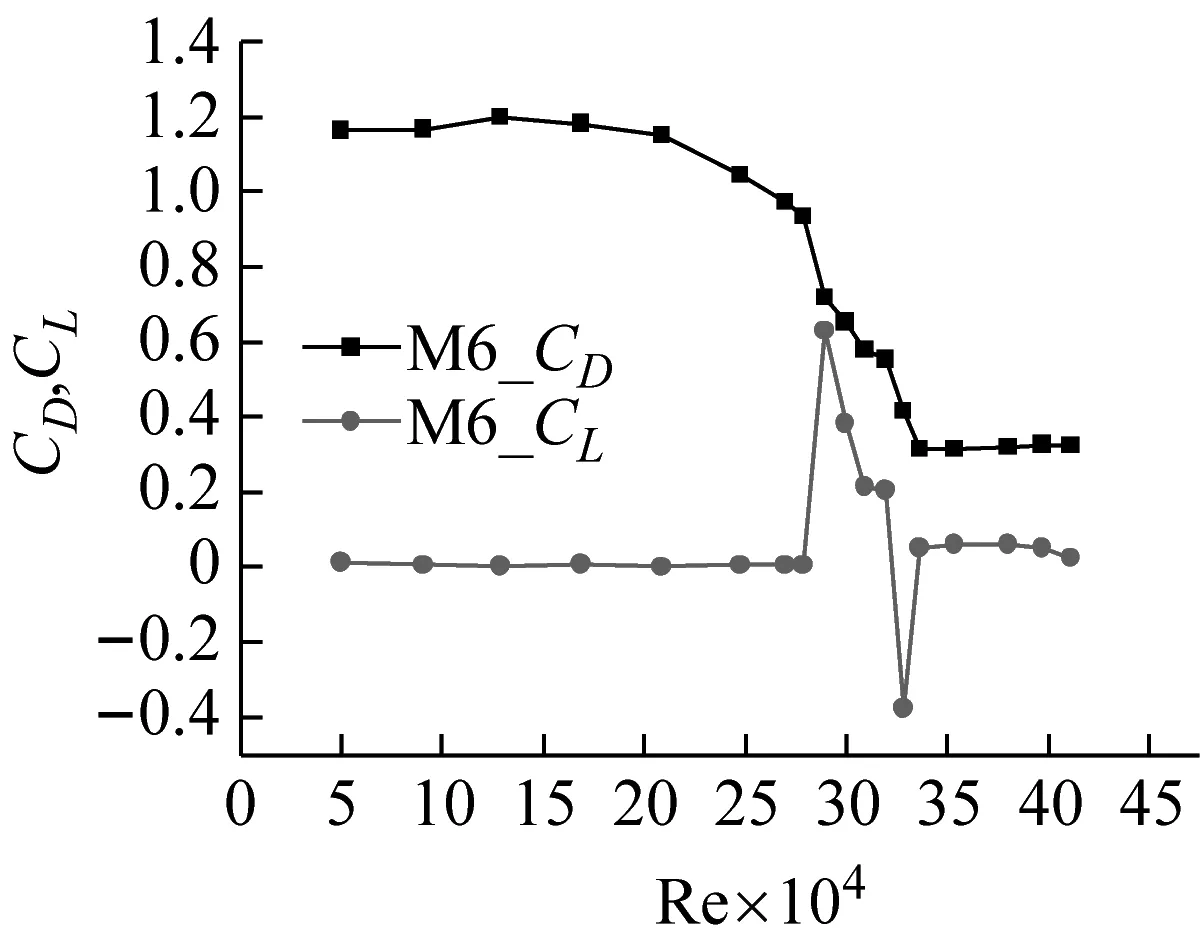
通过天平在斜拉索模型两端进行同步测力,得到了8种模型的阻力系数和升力系数随雷诺数的变化关系,如图5所示。
分析图5各个力系数随着雷诺数和粗糙度的变化,可总结得到如下几个方面的规律:
(1)每个模型在测试的雷诺数范围内,亚临界区阻力系数和升力系数基本保持不变,分别稳定在1.2和0附近;
(2)当进入临界区时,阻力系数和升力系数发生较大变化,随着阻力系数的下降,出现较大的升力系数,有的升力系数甚至要大于同样雷诺数对应的阻力系数;
(3)随着雷诺数的增大,阻力系数停止下降,改为缓慢增大,升力系数再次回到0值附近,进入超临界区。
(4)试验中发现升力的方向具有随机性,一个工况结束重新从低风速试验到高风速,升力的方向有可能同上一个工况的方向不同;即使在同一个试验过程中,随着风速的变化,升力也有改变方向的情况,如图5(f)。
(5)对于光滑模型来说,如图5(a),阻力的下降说明进入亚临界雷诺数区域,之后阻力系数有相对平稳的一段,这时升力系数最大,之后阻力系数继续快速下降,升力快速减小。整个过程对应文献[16]的从one bubble 到two bubble的流场变化。
(6)就整体规律而言,随着表面粗糙度的增大,阻力系数大幅下降和升力系数绝对值从零值附近大幅增大的雷诺数(即临界区开始的雷诺数)减小,阻力系数的最小值和升力系数(绝对值)的最大值也减小,雷诺数效应减弱,如图6所示。
从模型的力系数随雷诺数的变化关系中提取阻力系数的最小值和升力系数(绝对值)的最大值,将该数值随粗糙度的变化规律绘制于图7。
由图7可知,随着表面粗糙度的增大,阻力系数的最小值逐渐增大,升力系数(绝对值)的最大值逐渐减小。当粗糙度增大到一定程度时,升力系数变得很小,基本可以忽略。
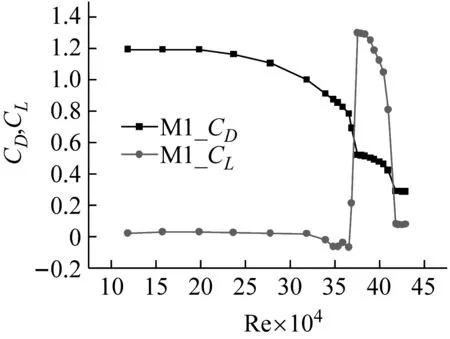
(a) M1
(b) M2

(c) M3
(d) M4
(e) M5
(f) M6

(g) M7

(h) M8图5 各模型的气动力系数随雷诺数的变化Fig.5 Aerodynamic force coefficient change with Re

图6 临界区开始的雷诺数随粗糙的变化Fig.6 Start of critical Re number valve change with surface roughness
3 苏通长江大桥斜拉索风荷载算例
如前所述,雷诺数效应的存在,使得最大风速对应的阻力不一定是整个风速范围内最大的阻力。如何计算从低风速到静阵风风速整个范围内的最大阻力值,是下面将要分析的问题。

图7 气动力系数随粗糙的变化Fig.7 Aerodynamic force coefficient pick valve change with surface roughness
以苏通长江公路大桥的斜拉索为例进行气动力计算。取其岸侧1号索A1,型号为PES7-139(直径D=105 mm)的斜拉索参数(斜拉索参数和桥梁设计参数见文献[17]),利用本研究的方法和《桥规》的方法对气动力进行计算比较[18]。为了理论分析的方便,此处没有考虑本桥斜拉索抑制风雨振而采取的气动措施,假定该斜拉索具有本文的不同粗糙度,用以说明计算方法。
假设来流与斜拉索轴向垂直,分别针对表面光滑和粗糙的模型进行计算,气动力系数按照模型M1和M4的结果分别取值,计算单位长度斜拉索的气动力。升力、阻力、合力以及《桥规》规定阻力算法得到的力汇总于图8。
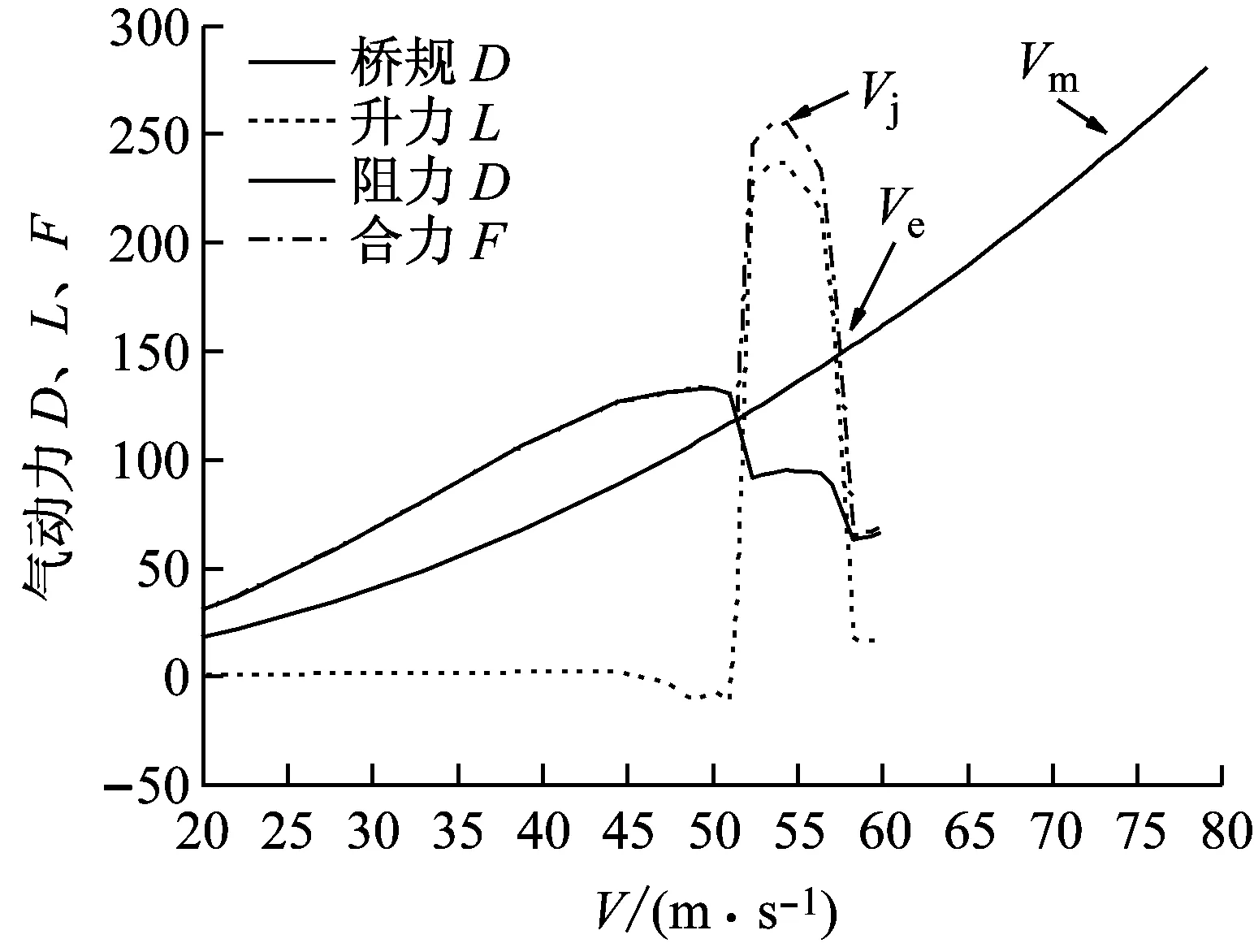
(a) M1模型光滑表面
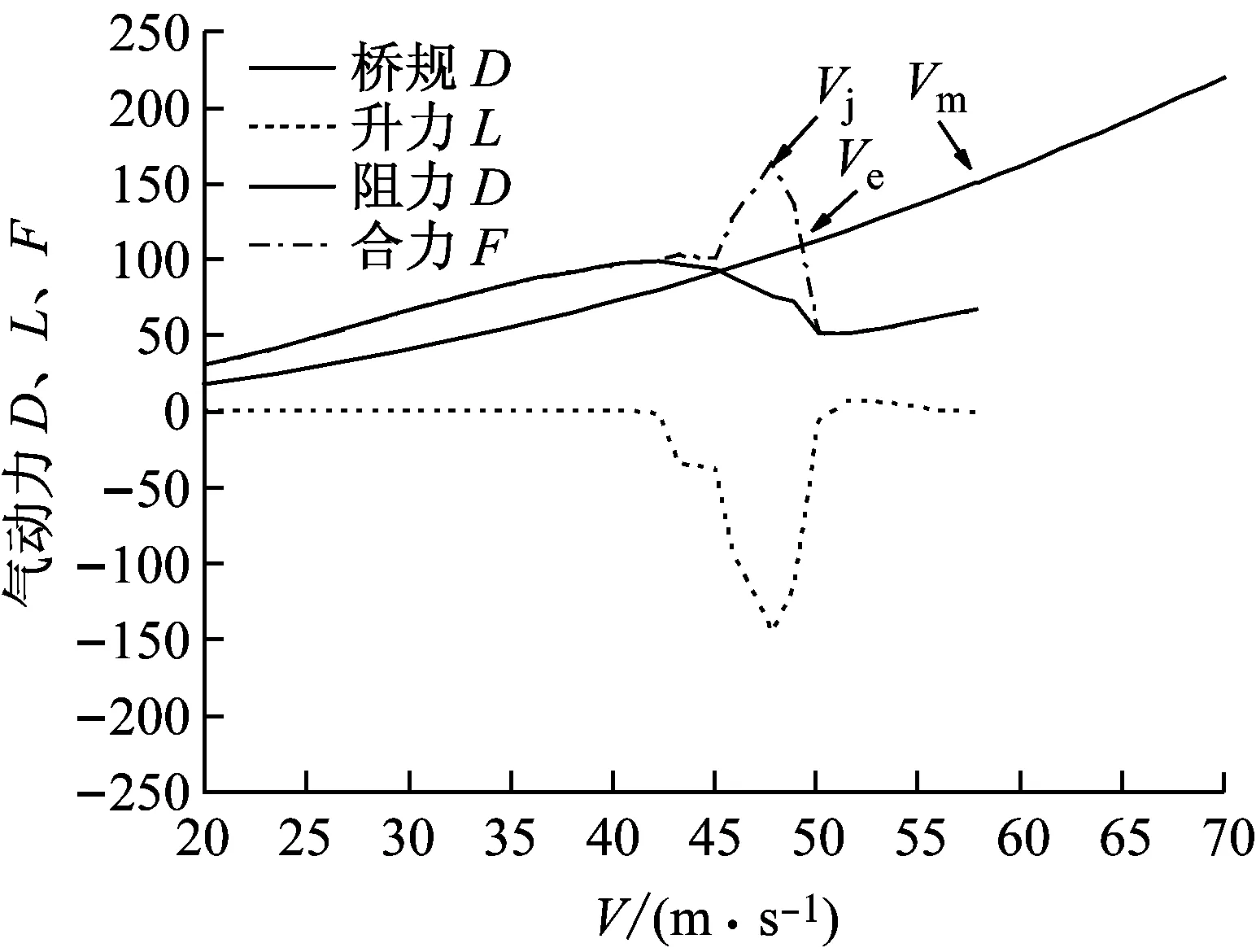
(b) M4模型粗糙表面图8 本方法气动力和按《桥规》算得的阻力Fig.8 Aerodynamic force by this research and by code
参照文献[18],图中规定了三个风速参数:Vj、Ve、Vm。Vj为当合力取得最大值时的风速;Ve为《桥规》气动力和合力值相等对应的风速;Vm为《桥规》气动力值和合力最大值相等时对应的风速。
其中试验的合力系数由式(2)计算。

(2)
如果将升力也作为总的风荷载的一项组成部分,由图8可知,当风速V
根据实际桥梁的设计资料和气象资料,算得上述各个风速的实际数值,并推广到各个粗糙度的工况中,归纳见表3所示。
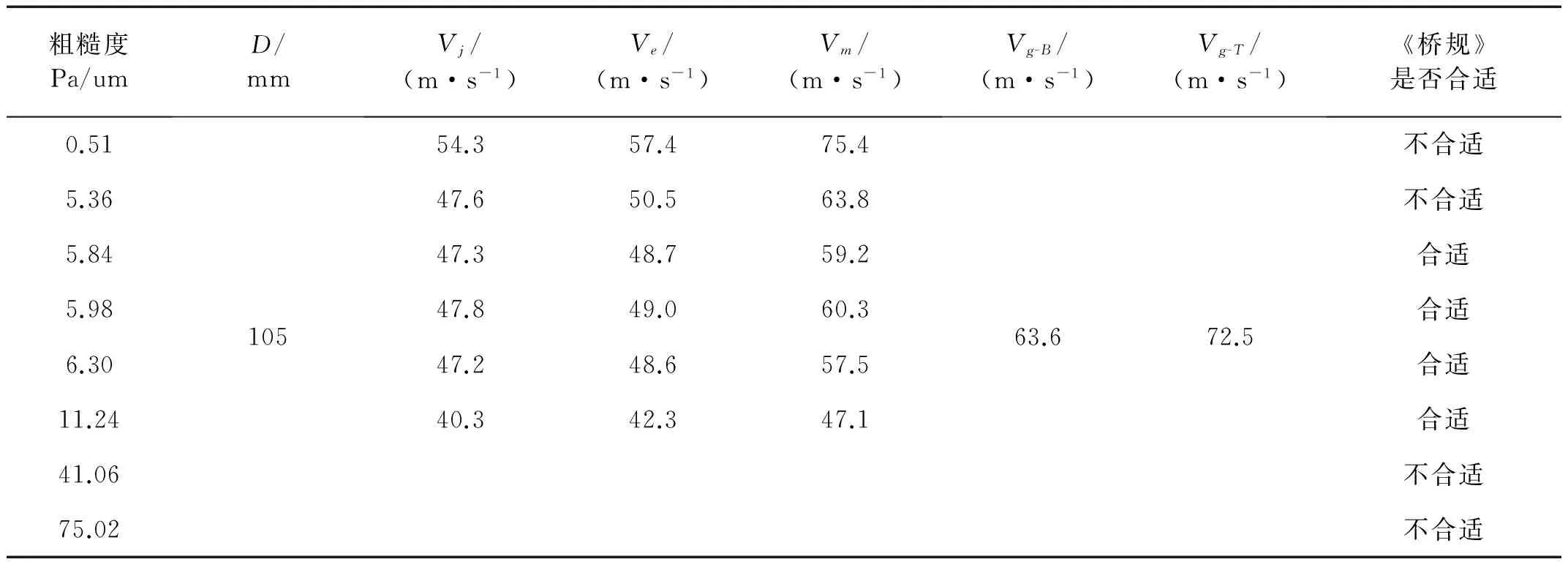
表3 苏通长江大桥A1斜拉索不同粗糙度时风荷载计算结果比较Tab.3 Wind load comparison of Sutong Yangtze River Bridge A1 Cable with different surface roughness
表3中:Vg-B为斜拉索下端锚固点的静风风速,Vg-T为斜拉索上端锚固点的静振风风速。根据《桥规》算的气动力如果小于本研究的气动力,则表中标注“不合适”;如果《桥规》算的的气动力如果大于本研究的气动力,则标注“合适”。
值得说明的是,这里是以苏通长江公路大桥的A1斜拉索的直径、桥梁和气候参数,假设其表面粗糙度数值的情况下进行了计算和分析。
根据上述研究,建议的实际工程斜拉索的气动力计算方法为:
首先,测试斜拉索表面的实际粗糙度,将该粗糙度同本文中列出的粗糙度进行对比,选择与其接近的,或者进行差值计算,得到斜拉索阻力系数和升力系数随雷诺数的变化曲线。因为斜拉索的表面粗糙度会随着服役期逐渐发生变化,因此测试时应考虑新出厂斜拉索和若干年服役期斜拉索的具体状况,将最不利状况作为计算依据。选择适当量程的表面粗糙度仪,作为测试的设备。
其次,根据设计资料和气象条件,计算确定静阵风风速对应的斜拉索的雷诺数数值;
第三,根据雷诺数数值对应的亚临界、临界和超临界区域,分别确定最大风荷载。如果对应亚临界区域,则静阵风风速对应的阻力和升力即为最大阻力和升力;如果雷诺数对应临界或者超临界区域,则应绘制阻力和升力从低风速到静阵风风速为止的整个变化曲线,在整个曲线中找到最大阻力和最大升力,该最大值有可能是静阵风风速对应的阻力和升力值,也可能是小于静阵风风速的某个特定风速对应的阻力和升力值(如图8中Vj对应的阻力和升力值)。
4 关于平均升力的讨论
本研究虽然获得了不同粗糙度下斜拉索的时间平均上的升力,但是该升力如何在风荷载的计算和内力及稳定验算中体现,也是值得讨论的问题。
从研究结果可知,对于二维圆柱结构来说,升力在横风向的两个方向上都有可能出现,而阻力都在顺风向出现。对于实桥来说,所有斜拉索的阻力在横桥向可以叠加,用于主梁位移和内力、稳定性的检算,而升力因为方向的不确定性无法在顺桥向简单叠加,因此升力仅可以用于索梁和索塔锚固端的检算等。
如果由于其它原因,例如斜拉索的垂度等影响,引起所有斜拉索的升力在某一个方向上出现的机会更大,则升力的顺桥向分力的叠加可以用于主梁轴向力及轴向稳定性的检算。
实际斜拉索在临界雷诺数区域平均升力的指向,以及在风荷载验算中的作用,是需要进一步研究的问题。
5 结 论
本文以8种不同粗糙表面的斜拉索为研究对象,研究了粗糙度指标对斜拉索气动力特性的影响,总结研究结果如下:
(1)不同表面粗糙度斜拉索的阻力系数和升力系数随雷诺数的变化规律基本一致,在亚临界区,阻力系数基本不变,升力系数基本为零;在临界雷诺数区,随着雷诺数的增大阻力系数减小,出现升力系数;之后阻力系数停止下降,变为缓慢增长状态,同时升力系数恢复到零值附近,进入超临界区。
(2)粗糙度对阻力系数和升力系数的数值有明显的影响:随着粗糙度的增加,阻力系数开始下降和升力系数开始出现的雷诺数数值(临界雷诺数开始的数值)变小、阻力系数的最小值增大、升力系数(绝对值)的最大值减小,雷诺数效应减弱。当粗糙度增大到一定程度时,升力系数变得很小,基本可以忽略。
(3)以苏通长江大桥的一个型号斜拉索为例,对斜拉索的气动力进行了计算,分析了不同粗糙度下阻力和升力的计算方法,并给出了建议:如果静阵风风速对应的雷诺数处于亚临界区,则静阵风风速对应阻力和升力即为最大值;如果静阵风风速对应的雷诺数处于亚临界或超临界区,则需要绘制从低风速到静阵风风速的整个风速范围内的阻力和升力曲线,从曲线中分别找到阻力和升力的最大值,作为最大阻力和最大升力值,该数值不一定是静阵风风速对应的阻力和升力值。
(4)对于实际斜拉桥的斜拉索,应该测试其实际粗糙度,将该粗糙度同本文中列出的粗糙度进行对比,选择与其接近的,或者进行差值计算,得到阻力系数和升力系数随雷诺数的变化曲线,进一步计算得到从低风速到静阵风风速整个风速范围内的最大阻力和最大升力,作为风荷载和稳定性验算的依据。
[1] 裴岷山,张喜岗,朱斌,等. 斜拉桥的拉索纵桥向风荷载计算方法研究[J]. 中国工程科学,2009, 11(3): 26-30.
PEI Minshan, ZHANG Xigang, ZHU Bin, et al. Study on longitudinal wind load calculation method of cables for cable-stayed bridge[J]. Engineering Sciences, 2009, 11(3): 26-30.
[2] ESDU. Mean forces, pressures and flow field velocities circular cylindrical structures: single cylinder with two-dimensional flow[R]. Item No. 80025, London: ESDU international, 1986.
[3] MATTEONI G, GEORGAKIS C T. Effects of bridge cable surface roughness and cross-sectional distortion on aerodynamic force coefficients[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104/105/106:176-187.
[4] LIU Qingkuan, ZHANG Feng, MA Wenyong. Experimental study on Reynolds number effect on dry cable galloping of stay cables[C]//Proceedings of the 13thInternational Conference on Wind Engineering. Amsterdam: The Netherlands, 2011.
[5] 希缪,著. 风对结构的作用-风工程导论[M]. 刘尚培, 项海帆,等译. 上海: 同济大学出版社, 1992: 111.
[6] 公路桥梁抗风设计规范:JTG/T D60-01—2004[S]. 北京:人民交通出版社,2004.
[7] POULIN S, LAREN A. Drag loading of circular cylinders inclined in the along-wind direction[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/10/11): 1350-1363.
[8] 李文勃, 林志兴, 杨立波. 超长斜拉索风阻系数及风雨激振的试验研究[J]. 振动测试与诊断, 2005, 25(2): 85-90.
LI Wenbo, LIN Zhixing, YANG Libo, Investigation on dray coefficients and rain-wind induced vibration of extremely long stay cables in wind tunnel[J]. Journal of Vibration Testing and Diagnosis, 2005, 25(2): 85-90.
[9] 林志兴, 杨立波, 李文勃. 斜拉索顺桥向风阻系数的试验研究[J]. 郑州大学学报(工学版), 2005, 26(1): 38-41.
LIN Zhixing, YANG Libo, LI Wenbo. Experimental study on drag coefficients of stay-cables corresponding to wind direction along the bridge central line[J]. Journal of Zhengzhou University(Engineering Science Editong), 2005, 26(1): 38-41.
[10] 王卫华, 李明水, 陈忻. 斜拉索的阻力系数的研究[J]. 空气动力学学报, 2005, 23(3): 389-393.
WANG Weihua, LI Mingshui, CHEN Xin. Investigation on drag coefficients of stay-cables[J]. Journal of Aerodynamics, 2005, 23(3): 389-393.
[11] ZDRAVKOVICH M M. Flow around circular cylinders[M]. London: Oxford University Press, 1997.
[12] CHENG S, IRWIN P A, JAKOBSEN J B, et al. Divergent motion of cables exposed to skewed wind[C]//Proceedings of the 5th International Symposium on Cable Dynamics. Santa Margherita, 2003: 271-278.
[13] LAROSE G L, JAKOBSEN J B, SAVAGE M G, et al. Wind tunnel experiments on an inclined and yawed stay cable model in the critical Reynolds number range[C]//Proceedings of the 5th International Symposium on Cable Dynamics. Santa Margherta, 2003: 279-286.
[14] 产品几何级数规范(GPS)表面结构 轮廓法术语、定义及表面结构参数:GB/T 3505—2009/ISO 4287:1997[S]. 北京:中国标准出版社,2009.
[15] 白桦. 影响桥梁及建筑结构风洞试验结果若干因素研究[D]. 西安: 长安大学, 2012.
[16] ZDRAVKOVICH M M. Flow around circular cylinders[M]. Oxford University Press, Incorporated, 1997.
[17] 饶华容, 邓惠斌. 千米级斜拉桥长索架设技术[J]. 中国工程科学, 2009, 11(3): 71-74.
RAO Huarong, DENG Huibin. Technology for long cable erection of a thousand-meter scale cable-stayed bridge[J]. Engineering Science, 2009, 11(3): 71-74.
[18] 刘庆宽, 乔富贵, 张峰. 考虑雷诺数效应的斜拉索气动力试验研究[J]. 土木工程学报, 2011, 44(11): 59-65.
LIU Qinkuan, QIAO Fugui, ZHANG Feng. Experimental study on cable aerodynamic forces considering Reynolds number effect[J]. China Civil Engineering Journal, 2011, 44(11): 59-65.
Aerodynamicforcesandwindloadscalculationmethodforstay-cableswithdifferentsurfaceroughness
LIU Qingkuan1, 2, YAN Xudong3, LI Conghui3, ZHENG Yunfei3, MA Wenyong1, 2, LIU Xiaobing1, 2
(1. Structural Health Monitoring Research Institute, Shijiazhuang Tiedao University, Shijiazhuang 050043, China; 2. Hebei Provincial Key Lab of Structural Health Monitoring and Control, Shijiazhuang 050043, China; 3. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)
Most parts of wind loads on a large span cable-stayed bridge are caused by cables. It is very important to determine wind forces on cables exactly for bridge design and analysis. Through wind tunnel tests, aerodynamic forces of 8 types of cables with different surface roughness were measured, the influences of surface roughness on Reynolds number effect and aerodynamic force characteristics were studied, the maximum wind load on a cable of a practical bridge was calculated. Results showed that the cable surface roughness has obvious effects on aerodynamic force; with increase in the cable surface roughness, Reynolds number effect decreases gradually; for different surface roughness of a cable, wind velocities corresponding to the maximum wind loads are different; for real bridge design, the maximum wind loads of cables should be determined according to their surface roughness.
stay-cables; aerodynamic forces; surface roughness; Reynolds number effect; maximum wind load
国家自然科学基金(51378323;51308359;51108280);河北省杰出青年基金(E2014210138)
2016-08-22 修改稿收到日期:2016-09-23
刘庆宽 男,博士,教授,1971年1月生
TH212;TH213.3
A
10.13465/j.cnki.jvs.2017.23.007
