基于贝叶斯理论的拉杆转子模态特性确认

边 涛， 谢寿生,2， 任立通， 张乐迪， 刘云龙

(1. 空军工程大学 工程学院， 西安 710038； 2. 先进航空发动机协同创新中心， 北京 100083)

基于贝叶斯理论的拉杆转子模态特性确认

边 涛1， 谢寿生1,2， 任立通1， 张乐迪1， 刘云龙1

(1. 空军工程大学 工程学院， 西安 710038； 2. 先进航空发动机协同创新中心， 北京 100083)

为了更真实地反映航空发动机高压转子拉杆结构的振动特性，对基于非线性弹塑性滑动模型中不确定参数的变化范围和规律进行研究，提出了基于贝叶斯理论的有限元模型模态特性确认方法。运用贝叶斯理论构建模态特性似然函数，通过马尔可夫蒙特卡罗方法求解不确定参数的后验概率分布，并建立基于稀疏网格配点法的替代模型，减少了蒙特卡罗方法的计算量，使该方法能够适用于大型复杂高压转子结构。以实际的航空发动机高压转子为例，确定高压转子结构特征频率的变化范围和规律，通过与实验模态特征频率对比，证明了该方法的有效性。

拉杆结构； 弹塑性滑动模型； 贝叶斯理论； 蒙特卡罗方法； 实验模态分析

建立准确的航空发动机高压转子拉杆结构有限元模型对于分析结构动态特性、提高装配水平具有十分重要的现实意义[1]。某型航空发动机高压转子采用拉杆结构增强了结构的刚度，但采用过盈联接的盘与盘之间、以及盘与拉杆之间的非线性接触面会使转子局部刚度降低。因此，如何建立非线性接触模型来准确描述拉杆结构接触面的复杂变化，如何在非线性模型的基础上进一步修正有限元模型使得结构预测响应与实际结构一致是亟需解决的问题。

文献[2]在理论模型研究中，将拉杆转子简化为非线性弹簧、非线性阻尼器和质量块的单自由度模型，较好地描述了拉杆连接的振动特性；文献[3-4]分析了拉杆转子的受力情况，然后考虑接触面接触刚度对转子动力特性的影响，将拉杆和接触面等效为一个铰链和一个抗弯弹簧，对传统的有限元方法进行了改进；文献[5]运用实验结果修正了有限元模型切向和法向的接触刚度，并且给出了预紧力和位移的变化对于能量消散特性和接触刚度的影响规律；文献[6]运用弹塑性滑动模型来描述拉杆转子的非线性特征，提出弹簧刚度矩阵和有限元模型刚度矩阵的融合修正方法，建立了包含接触的有限元刚度整体优化模型。这些基于确定性的模型修正虽然可以减小误差，使每个参数都收敛到一个确定的数值。但是，在高压转子拉杆结构中，由于接触面的复杂变化，导致拉杆结构的接触刚度以及实体单元的弹性模量的变化是未知的，而且这些参数在建模过程中是无法直接测量得到的，这样的修正过程只能得到高压转子在某种状态下的振动特性，无法得到在特征频率变化的真实状态下的振动特性。

本文在高压转子拉杆结构非线性弹塑性滑动模型[6]的基础上，提出一种基于贝叶斯理论的方法，对模型中不确定参数的变化范围和规律进行研究，通过计算确定了高压转子结构特征频率的变化范围和规律，从而更加真实地反映高压转子拉杆结构的振动特性。最后，以实例计算与分析证明了该方法的有效性。

1 高压转子拉杆结构弹塑性滑动模型

高压转子拉杆结构采用热套工艺进行装配，盘与盘之间通过拉杆连接，采用过盈联接的方式。根据对拉杆结构的受力分析，盘与盘之间的接触可以用一组沿挤压面均布的抗压弹簧和包含库伦摩擦力的弹塑性滑动模型[7]的阻尼器来表示，如图1所示。

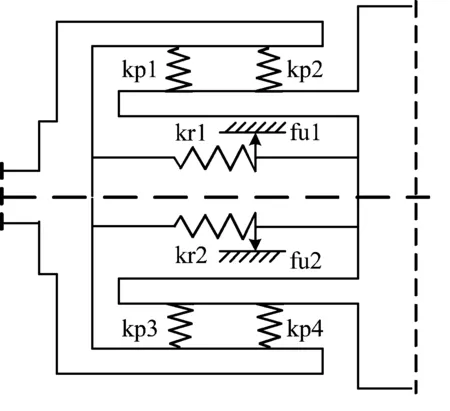
图1 基于弹塑性滑动模型的拉杆结构力学模型

Fig.1 Mechanical model of frictional contact between wheel disks based on elasto-slip model

其中，包含库伦摩擦力的弹塑性滑动模型如图2所示。该模型具有非线性滞后特性，如图3所示。

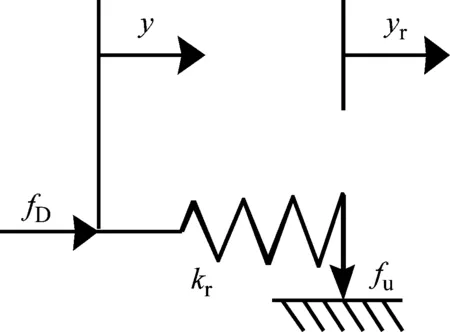
图2 弹塑性滑动模型的示意图Fig.2 Elasto-slip model

其中弹塑性滑动模型的耗散力fD符合如式(1)所示的定律

图3 弹塑性滑动模型的非线性滞后特性Fig.3 Nonlinear hysteretic behavior of the elasto-slip model

(1)

式中：kr为弹塑性模型的刚度值；fu为摩擦力；yn为通过测量变量y和内部变量yr得到的变换值，表达式为

yn=y-yr

(2)

该弹塑性滑动模型的耗散力定律如图4所示。

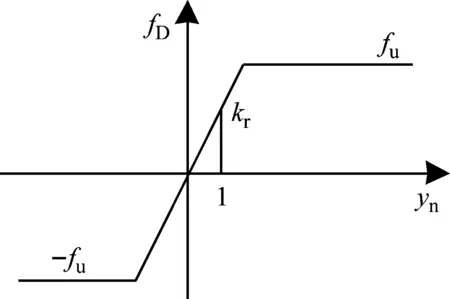
图4 弹塑性滑动模型的耗散力定律Fig.4 Constitutive law of elasto-slip model

因此，当|yn|≤fu/kr时，该阻尼器是线性的；而当|yn|>fu/kr时，该阻尼器产生滑动，能量通过摩擦力作用而耗散。

2 基于贝叶斯理论的模态特性似然函数

高压转子拉杆结构中接触面存在复杂的变化，导致拉杆结构的接触刚度以及实体单元的弹性模量的变化未知，使得结构的特征频率存在不确定性。本文基于贝叶斯理论构建模态特性似然函数，通过马尔可夫蒙特卡罗方法求解不确定参数的后验概率分布；其次建立基于稀疏网格配点法的替代模型，来减少蒙特卡罗方法的计算量。

2.1 贝叶斯理论

如果观测到事件A实际发生，要计算条件概率P(Bj|A)，则

(3)

上述公式称为贝叶斯(Bayes)公式[8]。

应用贝叶斯理论进行模型确认时，假设Bj表示模型的未知参数向量，以θ表示；A表示实验得到的数据，以d表示；先验分布P(Bj)表示关于未知参数θ的先验知识，是与该次实验结果无相关性的信息，主要来源于以往的实验结果或者建模人员的经验或者主观判断等，以p(θj)表示。

因此，当得到模型未知参数θ的先验分布，以及一组实验数据d后，则未知参数θ的后验分布可表示为

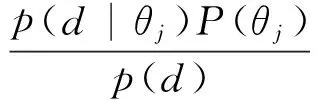
(4)

式中:p(d|θj)表示似然函数，定义了实验数据和模型计算结果之间的相似程度；p(θj|d)表示后验概率分布，能够反映模型经过修正后与实验数据之间的拟合程度。

2.2 构建模态似然函数

当模型参数存在不确定性时，导致模型计算结果与实验结果出现不一致的情况，表示为

y=q(θ)+e

(5)

式中，e表示模型误差。通常假设模型误差e服从正态分布，因此，未知参数的概率分布函数可表示为:

(6)

式中，N表示未知向量的长度。

当得到一组实验数据d={y1,y2,…,yj}时，似然函数可表示为

(7)

假设不同模态频率及其振型之间、不同数据集合之间相互独立，则通过模态特征频率及其振型的概率分布函数而构建的似然函数可表示为

(8)

模型计算特征频率和模态振型与实验结果之间的关系可分别表示为

(9)

(10)

假设特征频率和特征振型的误差函数服从正态分布，则基于特征频率的似然函数为

(11)

则基于模态特征振型的似然函数为

(12)

进一步简化为

(13)

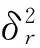
由式(7)、(8)可得，模态特性的似然函数表达式为

(14)

其中，

(15)

2.3 马尔可夫蒙特卡罗方法

后验概率的求解需要计算高维积分，故采用马尔可夫蒙特卡罗方法(Markov Chain Monte Carlo, MCMC)[9]。

马尔可夫蒙特卡罗方法是一种统计试验方法，其基本思想是构造一条具有指定的平稳分布的马尔可夫链，即它的转移分布收敛到后验分布。通过运行该马尔可夫链，使得链上取值的分布与其平稳分布一致时，将链上的取值作为来自其后验分布的样本。之后基于这些样本进行各种统计推断。

马尔可夫蒙特卡罗方法中常用的两种抽样方法为Gibbs抽样和Metropolis- Hastings(MH)抽样[10]。本文假设其条件分布均为满条件分布(full conditional distribution)。因此，采用Gibbs抽样算法为参数空间中的各个参数抽取样本。

Gibbs抽样过程如下所示：

步骤1: 给参数θ(0)和模态参数d(0)分别赋初始值，其中θ(0)和d(0)分别从参数θ和模态参数d的先验分布中随机抽取，并令j=1。

步骤2: 通过参数θ的满条件分布p(θ|d(j-1))为参数θ抽取样本，将抽到的样本值记为θ(j)。

步骤3: 将抽到的样本值θ(j)代入模态参数的满条件分布p(d|θ(j))，为模态参数d抽取样本，将抽到的样本值记为d(j)。

步骤4: 令j=j+1，返回STEP2，并依次循环得到以p(θ|d)为稳定分布的马尔可夫链。

2.4 基于网格配点法的替代模型

在基于贝叶斯方法的模型确认过程中，需要反复进行模态特征参数的求解，这对于大型复杂结构而言，计算量的巨大需求会使得模型确认过程无法进行。因此，本文提出基于稀疏网格配点法(Sparse grid collocation)[11]构建替代模型(Meta model)，代替有限元模型的模态特征参数的求解过程，减少计算量。采用Clenshaw-Curtis(CC)网格[12]，节点为

(16)

选择基函数为[13]：

(17)

根据网格节点的嵌套性，即Xi⊂Xi+1，各层级节点函数之间的差值:

Δi(f)=ui(f)-ui-1(f)

(18)

由于

ui-1(f)=ui(ui-1(f))

所以：

(19)

(20)

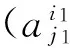
(21)

其中N维多变量的基函数可以表示为

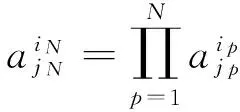
(22)

式中：p表示插值的层数；jp表示在p层的支持节点的位置。

根据式(14)，运用Smolyak[14]算法可以将稀疏网格配点法的插值函数表示为

Aq,N(f)=Aq-1,N(f)+ΔAq,N(f)

(23)

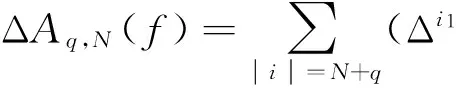
(24)

其中A-1,N=0，|i|=i1+…+iN。

该式可以进一步简化为

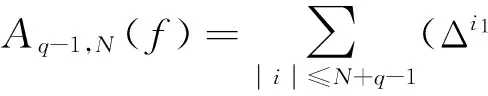
(25)

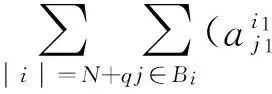
(26)

因此，建立的替代模型如下所示：

(27)

3 实例分析

3.1 模型确认

为验证本文提出的模型确认方法的有效性，对非线性接触刚度融合修正后的高压转子的有限元模型[6]进行模型确认分析。在螺栓接触分析过程中，由于没有更多先验知识，通常假设刚度系数的分布服从正态分布规律。Mantelli等[15]指出：螺栓结构的接触压力分布可以用威布尔分布很好地描述。因此，本文假设接触单元的刚度系数值的先验概率分布符合威布尔(Weibull)分布。即：

(28)

式中β>0,θ>0,δ表示位置参数；β表示形状参数；θ表示尺度参数。

假设实体模型中与螺栓接触部分的弹性模量服从正态分布，选择刚度融合修正后的参数值为概率分布的均值，并假设存在±10%的变化系数；高压转子部件的结构尺寸参数服从均匀分布，均值是名义尺寸，并假设存在±10%的上下界变化区间。通过实验模态分析得到10台高压转子的特征频率和相应的振型数据用于模型确认。

图5、图6分别表示了弹性模量和接触刚度参数的先验分布和后验分布的比较。

图5 弹性模量的先验分布和后验分布的对比图Fig.5 Comparison between prior and posterior distribution of elastic modulus

从图5中可以看出，应当将弹性模量先验分布的均值减少5%，使得模型的假设与实验模态参数更加吻合。从图6中可以看出，接触单元刚度的威布尔分布假设与实验结果的分布规律一致，证明了该假设的正确性。但是，应当将接触单元的刚度值提高5%，使得模型的取值与实验模态参数中反映的区间相重合。

图6 接触刚度参数的先验分布和后验分布的对比图Fig.6 Comparison between prior and posterior distribution of contacting stiffness

3.2 模态参数的一致性检验

经过弹性模量和接触刚度的修正后，再运用替代模型进行模态参数的求解，得到修正后模态参数的分布规律。图7～图12表示第一阶到第六阶特征频率的模态分布与实验数据的对比。

图中竖直实线代表有限元模型计算的初始值，竖直虚线表示10次实验得到的相应阶数的模态特征频率。

表1为计算与实验特征频率对比，表2为先验分布和后验分布对比结果的量化表示。其中d1、d2分别为10台高压转子实验模态特征频率到先验和后验分布中心的相对平均距离。

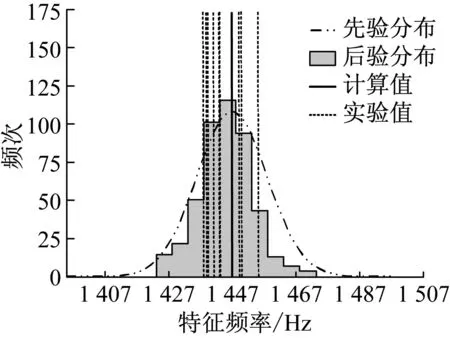
图7 第一阶特征频率的先验分布和后验分布的对比图

Fig.7 Comparison between prior and posterior distribution of the first mode frequency

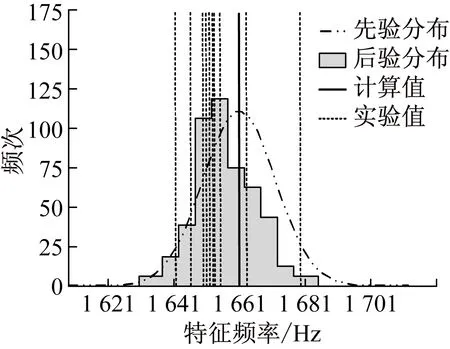
图8 第二阶特征频率的先验分布和后验分布的对比图

Fig.8 Comparison between prior and posterior distribution of the second mode frequency

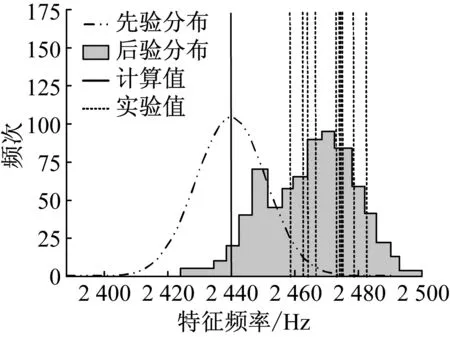
图9 第三阶特征频率的先验分布和后验分布的对比图

Fig.9 Comparison between prior and posterior distribution of the third mode frequency

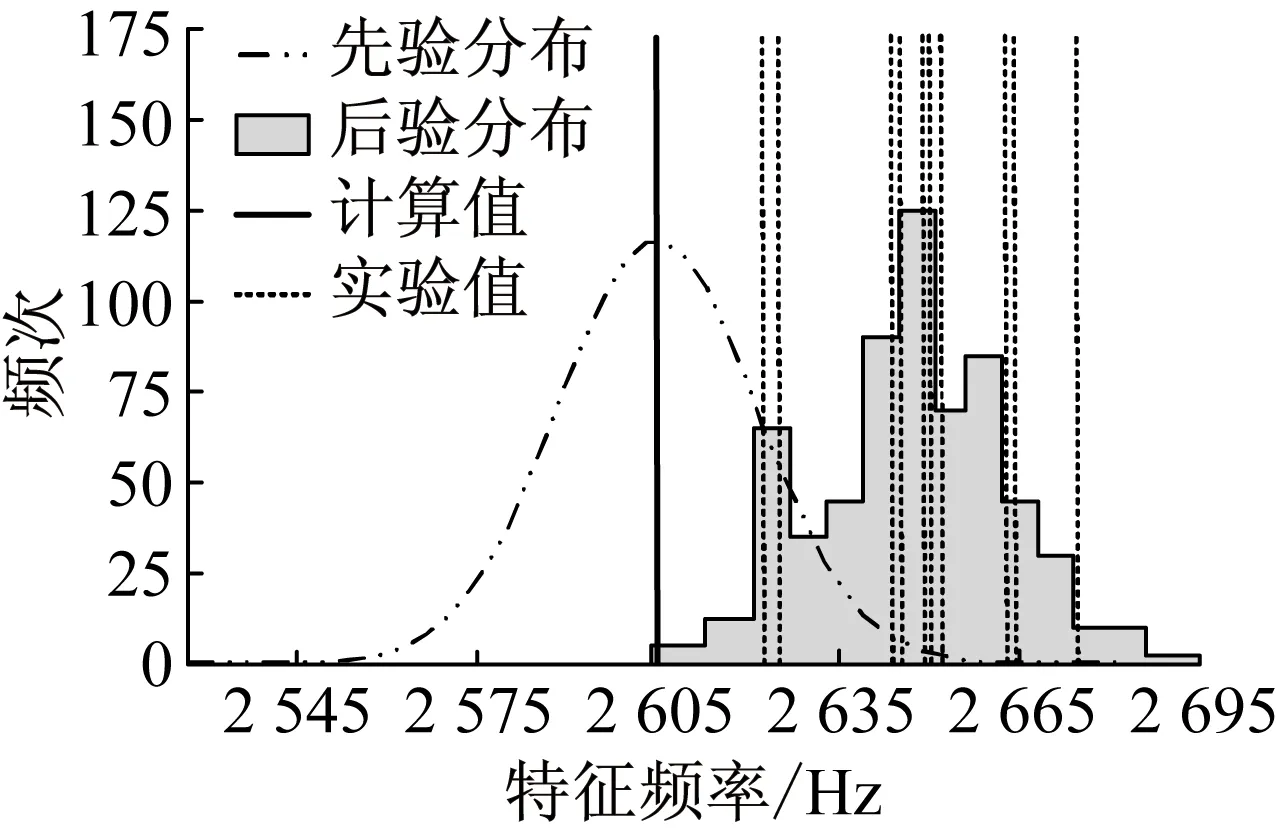
图10 第四阶特征频率的先验分布和后验分布的对比图

Fig.10 Comparison between prior and posterior distribution of the forth mode frequency

图11 第五阶特征频率的先验分布和后验分布的对比图

Fig.11 Comparison between prior and posterior distribution of the fifth mode frequency

图12 第六阶特征频率的先验分布和后验分布的对比图

Fig.12 Comparison between prior and posterior distribution of the sixth mode frequency

根据表1、表2以及图7～图12可以看出，第一阶和第二阶特征频率的模型计算结果与实验模态分析的结果误差小于1%，后四阶特征频率的模型计算结果与实验模态分析的结果误差则较大均超过1%(模型参数的不确定性)。因此，前两阶先验分布与后验分布基本吻合，后四阶先验分布与后验分布吻合度降低。从图9～图12第三阶到第六阶特征频率的变化可以看出，经过调整不确定参数的变化范围，特征频率的计算结果与实验结果的一致性增强，计算结果的分布移向实验数据所在的区间。

3.3 模态参数的对比分析

为验证基于贝叶斯理论的模型确认方法的准确性，将应用贝叶斯理论得到的模态参数的变化范围与ANSYS PDS[16]得到的模态参数的变化范围进行比较，其中不确定性参数的变化范围和规律依据经过贝叶斯理论优化后的结果输入。对比如图13～图18所示。

从图13到图18中可以看出，基于贝叶斯理论得到的模态参数变化范围与ANSYS PDS得到的模态参数变化范围基本一致,从而验证了基于贝叶斯理论的模型确认方法的准确性。

表1 计算与实验特征频率对比Tab.1 Comparison between computational and experimentalmode frequency

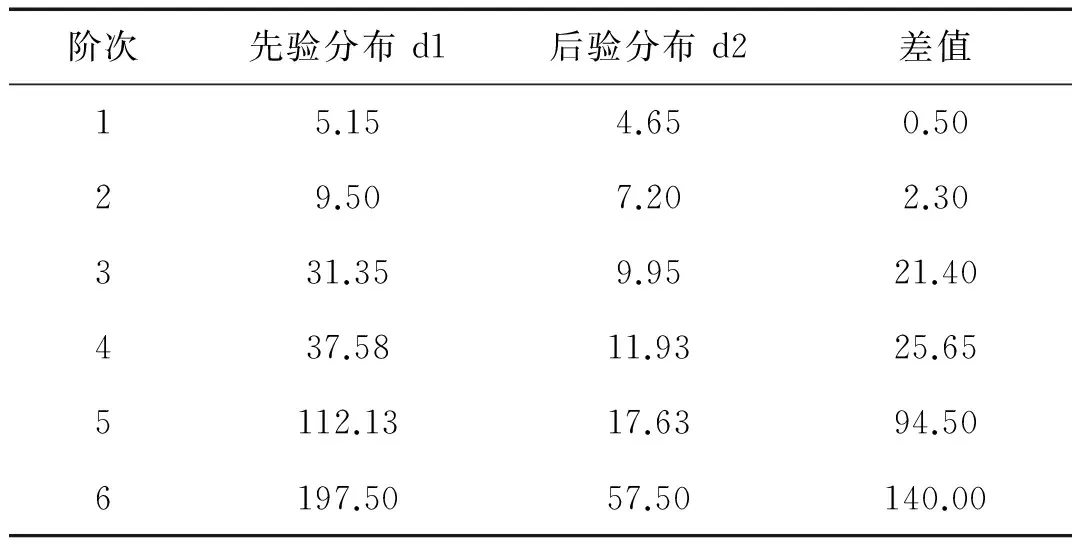
表2 先验分布和后验分布对比结果量化表示Tab.2 Comparison between prior and posteriordistribution

图13 第一阶特征频率的后验分布与ANSYS PDS的对比图

Fig.13 Comparison between posterior distribution and ANSYS PDS result of the first mode frequency

图14 第二阶特征频率的后验分布与ANSYS PDS的对比图

Fig.14 Comparison between posterior distribution and ANSYS PDS result of the second mode frequency

图15 第三阶特征频率的后验分布与ANSYS PDS的对比图

Fig.15 Comparison between posterior distribution and ANSYS PDS result of the third mode frequency

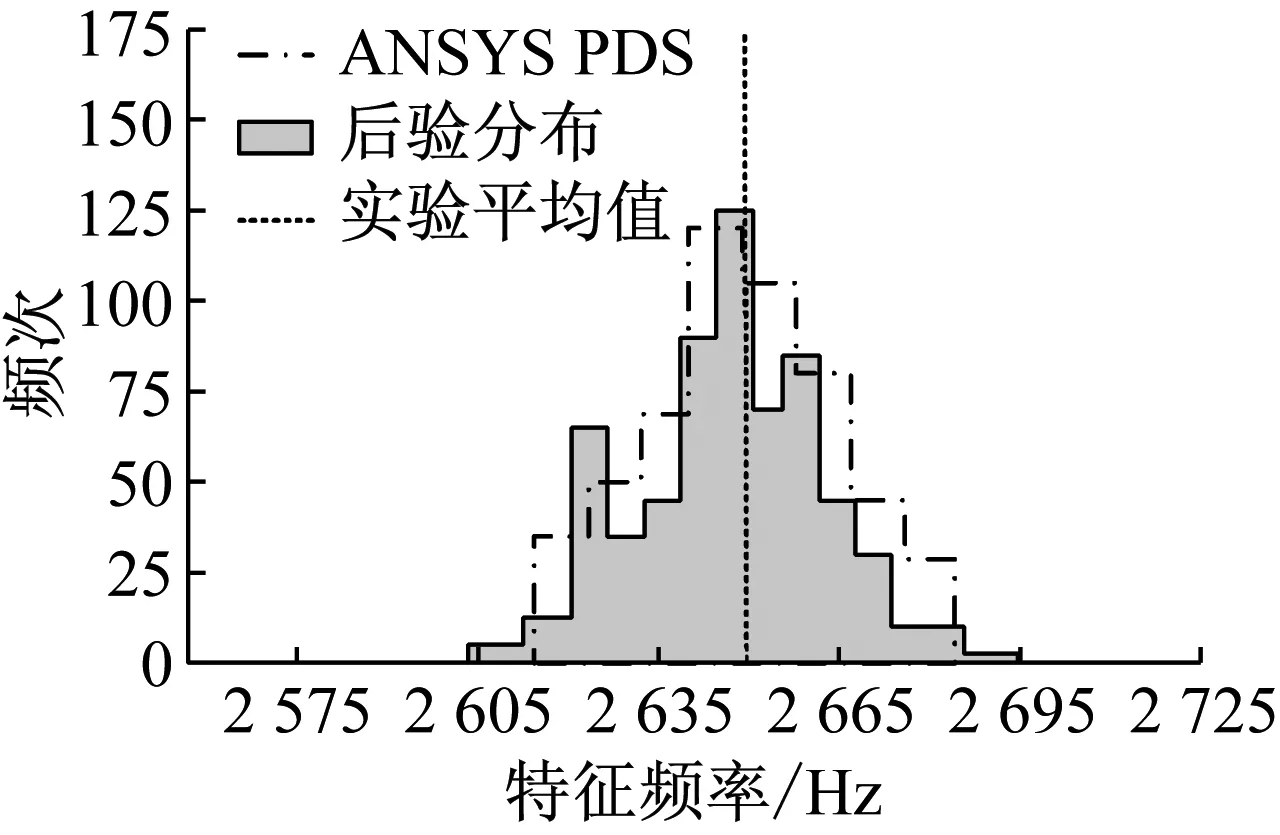
图16 第四阶特征频率的后验分布与ANSYS PDS的对比图

Fig.16 Comparison between posterior distribution and ANSYS PDS result of the forth mode frequency

图17 第五阶特征频率的后验分布与ANSYS PDS的对比图

Fig.17 Comparison between posterior distribution and ANSYS PDS result of the fifth mode frequency

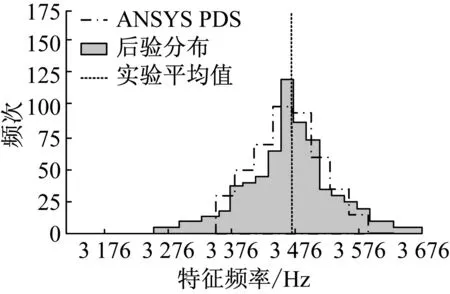
图18 第六阶特征频率的后验分布与ANSYS PDS的对比图

Fig.18 Comparison between posterior distribution and ANSYS PDS result of the sixth mode frequency

4 结 论

本文提出了一种基于贝叶斯理论的拉杆转子模态特性确认方法，通过实例计算，将特征频率的模型计算结果与实验模态分析的结果进行对比分析。结果表明：基于贝叶斯理论的有限元模态特性的确认方法不仅能够对建模过程中的不确定参数的假设进行检验，进而对参数进行优化，得到更准确的模态计算结果；而且，可以准确地确定高压转子特征频率的变化范围和规律。同时，建立的基于稀疏网格配点法的替代模型，能将基于贝叶斯理论的模型确认过程中最耗费时间的特征值的求解过程被极大地简化，使该方法能够适用于大型复杂高压转子结构，具有很大的现实意义，通过模态参数的对比分析也验证了该方法的准确性。

[1] 章圣聪,王艾伦.盘式拉杆转子的振动特性研究[J].振动与冲击,2009,28(4):117-120.

ZHANG Shengcong, WANG Ailun. Analysis of vibration characteristics of a disk-rod-fastening rotor [J]. Journal of Vibration and Shock,2009,28(4):117-120.

[2] 陈学前,杜强,冯加权.螺栓连接非线性振动特性研究[J].振动与冲击,2009,28(7):196-198.

CHEN Xueqian, DU Qiang, FENG Jiaquan. Nonlinear vibrational characteristic of bolt-joints [J]. Journal of Vibration and Shock,2009,28(7):196-198.

[3] 汪光明,饶柱石,夏松波.拉杆转子力学模型的研究[J]. 航空学报,1993,14(8): 419-423.

WANG Guangming, RAO Zhushi, XIA Songbo. The analysis of mechanical model of rod fastening rotor [J]. Acta Aeronautice et Astronautice Sinica,1993,14(8): 419-423.

[4] 饶柱石.拉杆组合式特种转子力学特性及其接触刚度的研究[D]. 哈尔滨:哈尔滨工业大学,1992.

[5] ABAD J, FRANCO J M, CELORRIO R, et al. Design of experiments and energy dissipation analysis for a contact mechanics 3D model of frictional bolted lap joints[J]. Advances in Engineering Software,2012,45(1):42-53.

[6] 张子阳,谢寿生,钱征文,等.拉杆结构中弹簧刚度和有限元模型刚度融合修正方法研究[J].振动与冲击,2011,30(11): 53-56.

ZHANG Ziyang, XIE Shousheng, QIAN Zhengwen, et al.Fusion stiffness modification of spring and FE model of rod fastening rotor[J]. Journal of Vibration and Shock, 2011,30(11):53-56.

[7] ZAPICO VALLE J L, ALONSO CAMBLOR R, GONZALEZ MARTINEZ M P, et al. A new method for finite element model updating in structural dynamics [J]. Mechanical Systems and Signal Processing,2010,24(7):2137-2159.

[8] 汪荣鑫.数理统计[M]. 西安:西安交通大学出版社, 1986,10.

[9] GILKS W R, RICHARDSON S, SPIEGELHALTER D J. Markov chain monte carlo in practice[M]. London:Chapman & Hall, 1996.

[10] LYNCH S M. Introduction to applied Bayesian statistics and estimation for social scientists[M]. New York: Springer,2007.

[11] MA X, ZABARAS N. An efficient Bayesian inference approach to inverse problems based on an adaptive sparse grid collocation method[J]. Inverse Problems 2009, 25(3): 1-27.

[12] KLIMKE A, WOHLMUTH B. Algorithm 847: spinterp: Piecewise multilinear hierarchical sparse grid interpolation in matlab[J]. ACM Transactions on Mathematical Software,2005,31(4):561-579.

[13] NOBILE F, TEMPONE R, WEBSTER C. The analysis of a sparse grid stochastic collocation method for partial differential equations with high-dimensional random input data[R]. Sandia report, SAND 2007-8093,2007.12.

[14] SMOLYAK S A. Quadrature and interpolation formulas for tensor products of certain classes of functions[J]. Dokl. Akad. Nauk SSSR,1963(4): 240-243.

[15] MANTELLI M B H, MILANEZ F H, PEREIRA E N. Statistical model for pressure distribution of bolted joints[J]. Journal of Thermophysics and Heat Transfer,2010,24(2):432-437.

[16] REH S, BELEY J, MUKHERJEE S, et al. Probabilistic finite element analysis using ANSYS[J]. Structural Safety, 2006, 28(1/2): 17-43.

Modalcharacteristicsconfirmationofarod-fasteningrotorbasedonBayesiantheory

BIAN Tao1, XIE Shousheng1,2, REN Litong1, ZHANG Ledi1，LIU Yunlong1

(1. The Engineering Institute, Air Force Engineering University, Xi’an 710038, China;2. Collaborative Innovation Center for Advanced Aero-Engine, Beijing 100083, China)

In order to reflect the real vibration characteristics of rod-fastening rotors of high pressure spool(HPS) in an aero-engine, Here, a FE (finite element) model modal characteristics confirmation method based on Bayesian theory was proposed. An elastoplastic slip model with non-linear hysteretic behavior was introduced to determine regions of uncertain parameters. According to this model, the likelihood function for modal data characteristics was built using Bayesian theory, Bayesian updating procedure was implemented using a multi-level Markov chain Monte Carlo (MCMC) algorithm. In addition, the adaptive hierarchical sparse grid collocation (ASGC) method was used to construct the stochastic surrogate model for the posterior probability distribution calculation of uncertain parameters, it reduced the amount of computation of the MCMC for large FE models like HPS. The real example of an aero-engine’s high pressure rotor was given, the results using this modal characteristics confirmation method were compared with its test data, it was shown that the proposed method can determine regions and varying law of HPS feature frequencies, its effectiveness is verified.

rod-fastening rotor; elastoplastic slip model; Bayesian theory; Markov chain Monte Carlo method; test modal analysis

国家自然科学基金(51476187；51506221)

2016-08-12 修改稿收到日期：2016-09-26

边涛 男，硕士生，1992年生

谢寿生 男，教授，博士生导师，1959年生

V23

A

10.13465/j.cnki.jvs.2017.23.014