生活中的相似

文/邓革周

生活中的相似

文/邓革周

相似三角形是初中数学的重要内容，是研究几何与图形的基础，它的应用很广泛.现把相似三角形在生活中的应用归类如下.

一、测量高度

例1如图1，小明为了测量一凉亭的高度AB（顶端A到水平地面BD的距离），在旁边放置一个与凉亭的台阶BC等高的台阶DE（DE=BC=0.5米，A、B、C三点共线），把一面镜子水平放置在平台上的点G处，测得CG=15米，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A，测得EG=3米，小明身高1.6米.凉亭的高度AB为（ ）

A．8.5米. B．9米. C．9.5米. D．10米.

解：由题意得∠AGC=∠FGE，

∠ACG=∠FEG=90°，

∴△ACG∽△FEG，

∴AB=AC+BC=8+0.5=8.5（米）．选A．

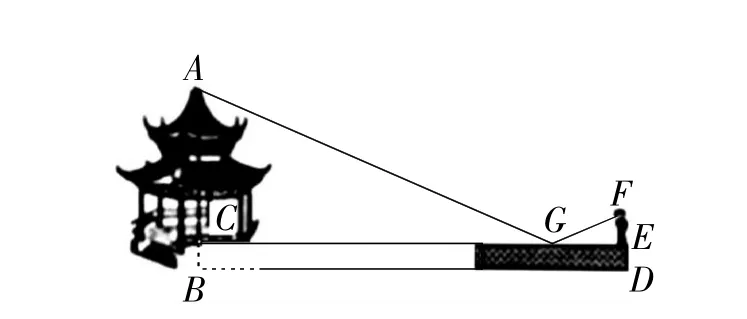
图1

评点：本题考查了相似三角形的应用，解题的关键是根据光的反射定理找到相似三角形.

二、测量宽度

例2如图2，M、N为山两侧的两个村庄，两村的交通不方便，根据国家的惠民政策，政府决定打一直线涵洞.工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米，AN=1.8千米，AB=54米，BC=45米，AC=30米，求M、N两点之间的直线距离．

解：在△ABC与△ANM中，

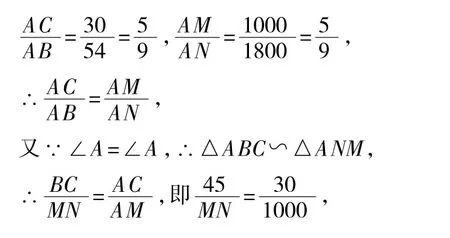
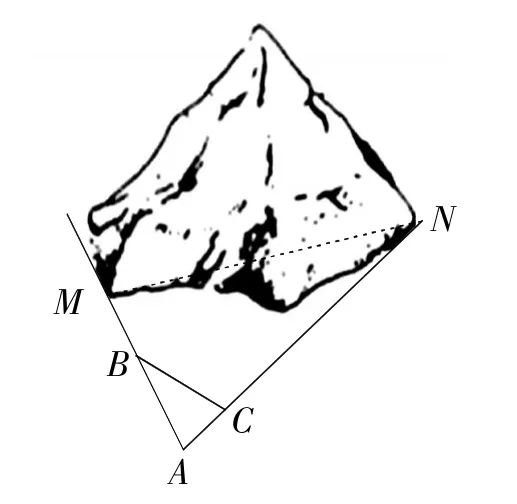
图2

解得MN=1500（米）.

答：M、N两点之间的直线距离是1500米.

评点：从公共角（∠A）出发，利用“两边对应成比例且夹角相等”构造相似三角形，从而求解.

三、确定裁剪方案

例3直角三角形的铁片ABC的两条直角边BC、AC分别为6和8，如图3所示.现分别采用图3、图4两种方法，剪出一块正方形铁片，为使剩下的边角料较少，试比较哪种剪法合理，并说明理由．

解：在图3中，设DE=CD=EF=CF=x.

图3

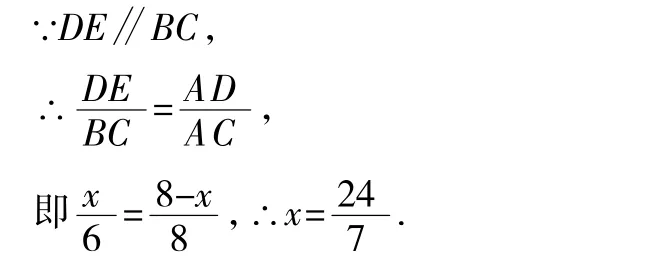
在图4中，作CM⊥AB，垂足为M，交DE于N.设正方形的边长为y．

在Rt△ABC中，∵AC=8，BC=6，

∵x＞y，∴图3中正方形的面积大，即剩下的边角料较少.

故图3的剪法合理．

图4

评点：要求边角料较小，就是使正方形的面积较大，即边长较长.

四、资金预算

例4石山社区拟筹资金4500元，计划在一块上底、下底分别为10m、20m的梯形空地上种植花木（如图5所示）．他们想在△AMD和△BMC种植单价为20元/m2的太阳花．当△AMD种满花后，花了1000元钱.请预算一下，若继续在△BMC上种植同样的太阳花，资金是否够用？并说明理由．

解：（1）∵四边形ABCD是梯形，∴AD∥BC，

∴∠MAD=∠MCB，∠MDA=∠MBC，

∴△AMD∽△CMB，

图5

当△AMD种满花后，花费1000元，所以,种满△BMC所需费用为1000×4=4000元.

而1000+4000＞4500,资金不够用．

评点：灵活运用“相似三角形的面积比等于相似比的平方”的结论是解题的关键．

五、房屋采光

例5已知，如图6，CD为一幢3米高的温室，其南面窗户的底框G距地面1米，CD在地面上留下的最大影长CF为2米，现欲在距C点7米的正南方A点处建一幢12米高的楼房AB（设A，C，F在同一水平线上）．

图6

（1）按比例较精确地作出高楼AB及它的最大影长AE；

（2）若大楼AB建成后是否影响温室CD的采光，试说明理由．

解:（1）作出高楼AB及最大影长AE如图7所示.

(2)如图7，∵HE∥DF，HC∥AB，

图7

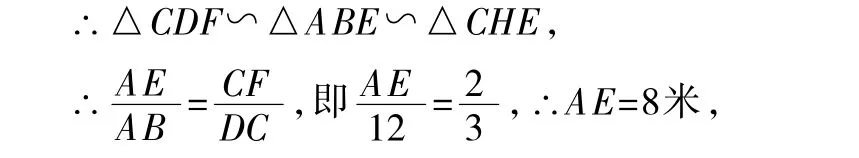
由AC=7米，可得CE=1米，

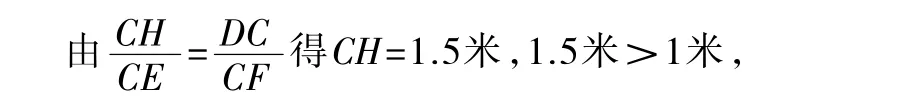
故影响采光．

评点：同一时刻同一地点，物体的高与其影长的比值不变.

王二喜