First-principles investigation on the structural stability， electronic structure and optical properties of MgxZn1-xSe alloys

YU Zhiqiang， ZHANG Changhua， LIAO Honghua， LI Shidong， LANG Jianxun

(1.Department of Electrical Engineering， Hubei University for Nationalities， Enshi， Hubei 445000， China; 2.School of Optical and Electronic Information， Huazhong University of Science and Technology， Wuhan 430074， China)

First-principlesinvestigationonthestructuralstability，electronicstructureandopticalpropertiesofMgxZn1-xSealloys

YU Zhiqiang1，2*， ZHANG Changhua1*， LIAO Honghua1， LI Shidong1， LANG Jianxun1

(1.Department of Electrical Engineering， Hubei University for Nationalities， Enshi， Hubei 445000， China; 2.School of Optical and Electronic Information， Huazhong University of Science and Technology， Wuhan 430074， China)

The structural stability， electronic structure and optical properties of zinc-blende MgxZn1-xSe alloys are determined using first-principles calculations based on the density functional theory. The results show that both the pure and Mg-doped ZnSe alloys display a direct band structure. The band gapEgand formation energyEbof MgxZn1-xSe alloys are able to be evaluated by the first order equationEg=1.30+1.34xand the second order polynomialEb=-1.48+0.60x-0.27x2， respectively. The top of valence band is mainly contributed by the Se 4p and Zn 3p states， while the bottom of conduction band is primarily occupied by the Zn 4s， Zn 3p and Se 4s states in MgxZn1-xSe alloys. Moreover， the static dielectric constant decreases and the optical absorption spectrum has a blue-shift obviously with the increasing Mg dopant compositionxin MgxZn1-xSe alloys. The calculated results provide important theoretical guidance for the applications of MgxZn1-xSe alloys in optical detectors.

first-principles; MgxZn1-xSe alloys; electronic structure; optical properties

The group II-VI semiconductors with a large direct band structure at the room temperature and their alloys have attracted considerable interest due to their potential applications in integrated optical devices， optical wave guides， ultraviolet photodetectors， photovoltaic devices， semiconductor photocatalysts， luminescence biological tags and blue-green laser diodes[1-4]. As one of the typical II-VI semiconductors， the zinc-blende ZnSe has been deemed to be a prospective optical material derives from its wide direct band gap of 2.70 eV and large excitation binding energy of 21 meV. Meanwhile， zinc-blende ZnSe has been widely applied in semiconductor photocatalysts， light emitting diodes， ultraviolet photodetectors， solar cells and blue-green laser devices[5-9].

In recent decades， people have found that the electronic structure and optical properties of zincblende ZnSe can be effectively tuned by introducing some impurities or defects. Zhang et al[10]reported that the incorporation of nitrogen composition has resulted in a phase transformation of ZnSe films from zinc-blende to wurtzite. Amin et al[11]. predicted a ferromagnetic nature and the reduced band gap of zinc-blende ZnSe due to the addition of some transition metal elements such as Fe， Co， and Ni， which originates from the strong sp-d exchange interaction between the band electrons and localized 3d states of dopants. The alkaline earth metal elements have no localized d states， which can be taken as the prospective dopants for modifying the properties of semiconductors. Archana et al[12]shown experimentally an increased band gap of ZnSe nanoparticles with the Mg doping of alkaline earth metal. However， the theoretical investigation on the structural stability， electronic structure and optical properties of MgxZn1-xSe alloys has not been reported in detail．

In the present paper， we performed the first-principles calculations based on the density functional theory to determine the band structure， density of state and optical properties of zinc-blende MgxZn1-xSe alloys， which provides useful theoretical guidance for the applications of zinc-blende MgxZn1-xSe alloys in optical detectors．

1 Models and methods

The cubic zinc-blende ZnSe has an F-43m space group and the pure ZnSe with 1×1×1 cubic unit cell is shown in Fig.1. The zinc-blende MgxZn1-xSe alloys can be obtained by the Zn atoms replaced for Mg atoms and the MgxZn1-xSe alloys models are constructed in the 2×2×1 ZnSe supercell. We directly employ four， eight and twelve Mg atoms to replace Zn atoms in the 2×2×1 ZnSe supercell correspond to Mg dopant composition x at 0.25， 0.50 and 0.75， respectively.

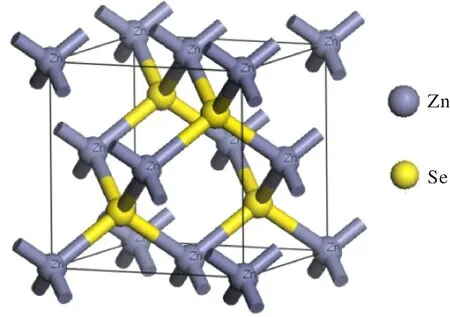
Fig.1 The crystal structure of pure ZnSe unit cell

The first-principles calculations based on the density functional theory[13]are performed using the Cambridge Sequential Total Energy Package (CASTEP) code and the exchange correlation function is implemented by the generalized gradient approximation[14](GGA) upon the scheme of Perdew-Burke-Ernzerhof (PBE). The Brillouin zone integrations with 4×4×4 k-point meshes are performed in the framework of Monkhorst-Pack meshes for the MgxZn1-xSe alloys. The convergence criterion of the plane wave energy cutoff is chosen to be 420 eV， while the convergence accuracy of the maximum force between the atoms is less than 0.02 eV/Å and the self-consistent convergence criteria is 1.5×10-6eV/atom. Moreover， the Zn 3d104s2states， Se 4s24p4states and Mg 2p63s2states have been used for the pseudopotential configurations， respectively.

2 Results and discussion

2.1 Geometry optimization and structural stability

The optimized lattice constant and formation energy of MgxZn1-xSe alloys have been shown in Table 1. It is observed that the optimized lattice constant of pure ZnSe with a value of 0.571 4 nm is in reasonable agreement with the experimental data of 0.566 7 nm[15]in the theoretical error distribution around 0.8%， while the lattice constants of MgxZn1-xSe alloys slightly increase with the increases of Mg dopant composition. In particular， the optimized lattice constant and its fitting curves of MgxZn1-xSe alloys varies with the dopant compositionxare plotted in Fig.2. It is clear that the lattice constant can be evaluated by the second order polynomiala=0.5714+0.0173x+0.01x2with dopant compositionxranges from 0 to 0.75. It clearly shows the nonlinear relation between the lattice constant and dopant compositionxof MgxZn1-xSe alloys， which relates to the lower electronegativity of Mg atoms compared with Zn atoms.

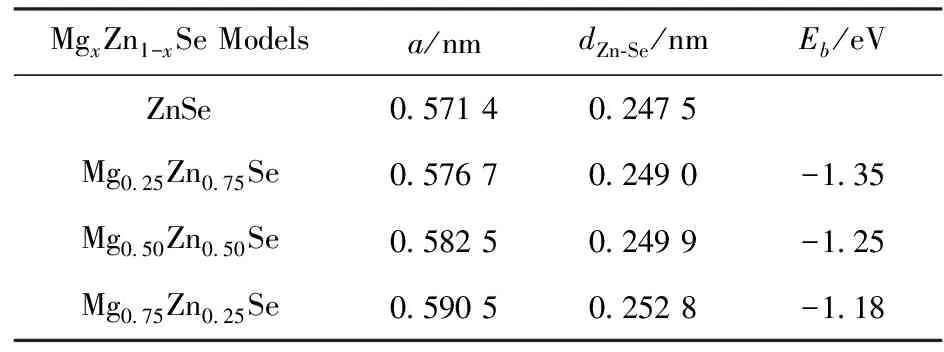
Tab.1 The optimized lattice constant and formation

Moreover， compared with the structural stability of MgxZn1-xSe alloys， the formation energyEbof an impurity Mg is described as

Eb=Et-Ep-EMg+EZn.

(1)

whereEtis the total energy of the supercell containing one Mg， andEpis the total energy of the supercell containing only bulk ZnSe.EZnandEMgare the chemical potentials of Zn and Mg， respectively.

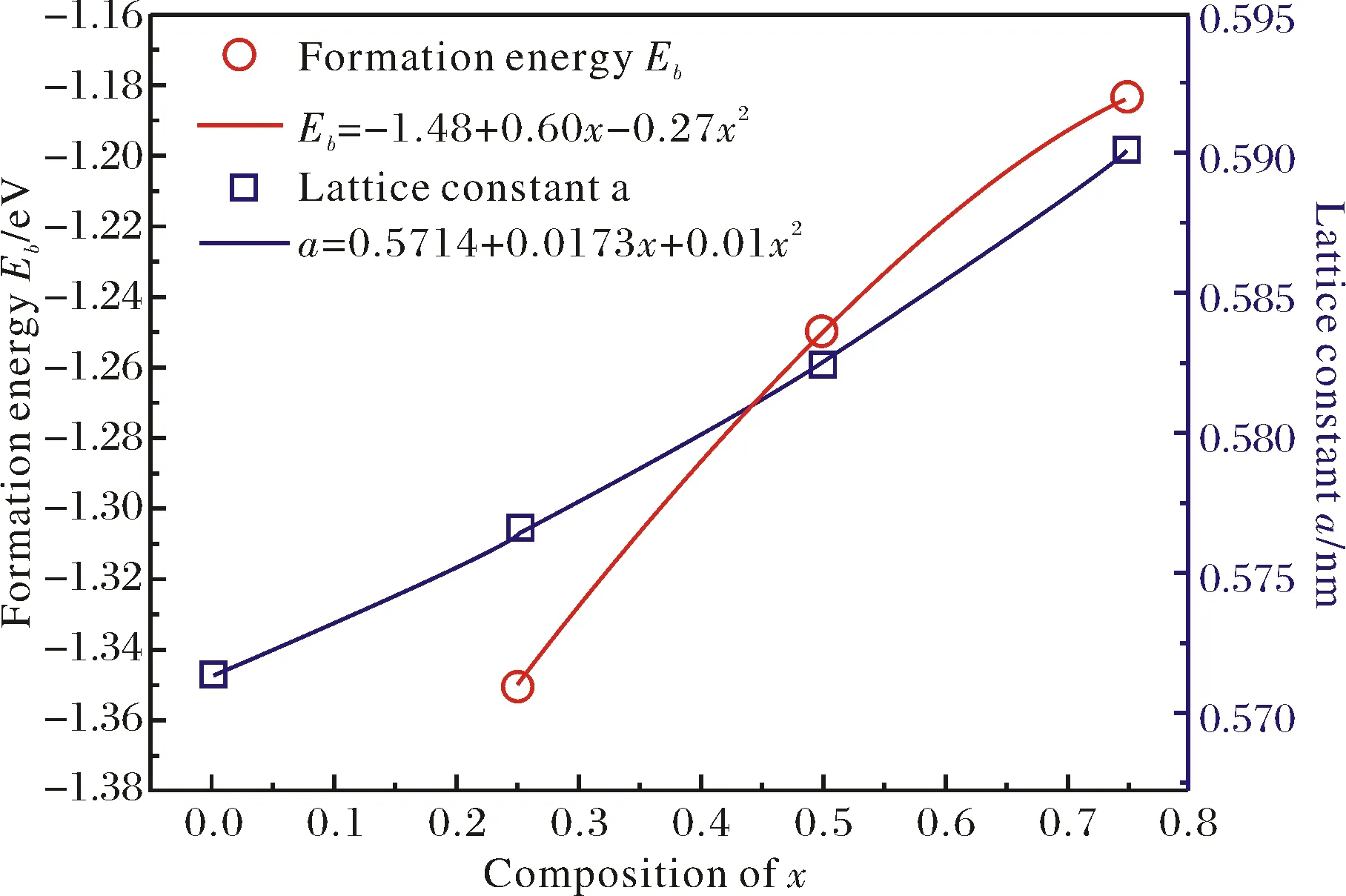
Fig.2 The formation energy and Lattice constant of MgxZn1-xSe alloys

It is clearly seen that the formation energyEbof MgxZn1-xSe alloys increases from -1.35 eV to -1.18 eV with an increase in Mg doping concentrationxas shown in Tab.1 and Fig.2， which indi-

cates that the structural stability of MgxZn1-xSe alloys decreases on the basis of the lowest energy principles. Meanwhile， the formation energyEbcan be evaluated by the second order polynomialEb=-1.48+0.60x-0.27x2as shown in Fig.2 and the most possible stable structure for MgxZn1-xSe alloys is displayed in Mg0.25Zn0.75Se.

2.2 Electronic structure

The band structure and density of states for MgxZn1-xSe alloys are depicted in Fig.3-Fig.8， respectively. As shown in Fig.3， both the pure and Mg-doped ZnSe alloys show a direct band gap along theΓ-Γpath in the first Brillouin zone and the band gap of MgxZn1-xSe alloys increases with the increasing Mg dopant compositionx. In addition， the band gap of pure ZnSe is 1.30 eV， which is close to the earlier band gaps of 1.20 eV[11]and 1.43 eV[16]. However， the band gap of 1.30 eV is lower than the experimental data of 2.70 eV due to the limitation of density functional theory， which originates from the exchange correlation function has been underestimated in the density functional theory．

Fig.3 The band structures of (a) pure ZnSe， (b) Mg0.25Zn0.75Se， (c) Mg0.50Zn0.50Se and (d) Mg0.75Zn0.25Se

The band structures of pure and Mg-doped ZnSe alloys are shown in Figs.3(a)～3(d)， respectively. It is clear that the band gap of MgxZn1-xSe alloys increases from 1.30 eV to 2.30 eV with the increasing Mg dopant composition x ranges from 0 to 0.75. In particular， the band gap and its fitting curves of MgxZn1-xSe alloys varies with the dopant compositionxare plotted in Fig.4. It is shown that the band gap of MgxZn1-xSe alloys can be approximated by the first order functionEg=1.30+1.34x， whereEgis the band gap and Mg dopant compositionxranges from 0 to 0.75. It clearly elucidates the linear relation between the band gap and dopant compositionxof MgxZn1-xSe alloys， which is mainly induced by the effects of electronic hybridization in MgxZn1-xS alloys．

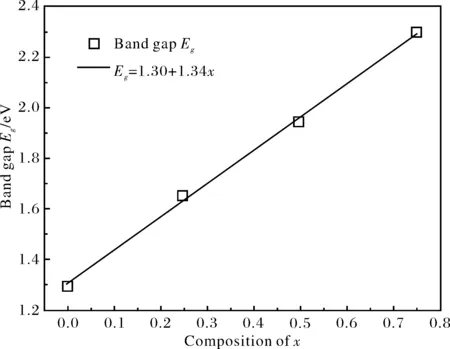
Fig.4 The band gap of MgxZn1-xSe alloys

In order to analyze the electronic properties of pure and Mg-doped ZnSe alloys. The total density of states (TDOS) and partial density of states (PDOS) for pure ZnSe are displayed in Fig.5(a)～5(c). It is observed that the conduction band of pure ZnSe is dominated by the Zn 4s， Zn 3p and Se 4s states， while the valence band is mainly separated into two regions. The Se 4s states primarily occupied the lower energy region at around -12 eV， and the Se 4p， Zn 3p， Zn 4s and Zn 3d states have determined the higher energy region ranges from -7 eV to 0 eV in the valence band. Moreover， the conduction band minimum (CBM) along theΓ-Γpath 1.30 eV above the Fermi surface and it is mainly derived from the Zn 4s， Zn 3p and Se 4s states， while the valance band maximum (VBM) along theΓ-Γdirection that near the Fermi surface and it is primarily occupied by the Se 4p and Zn 3p states， which construct the direct band structure of pure ZnSe as shown in Fig.3(a)．

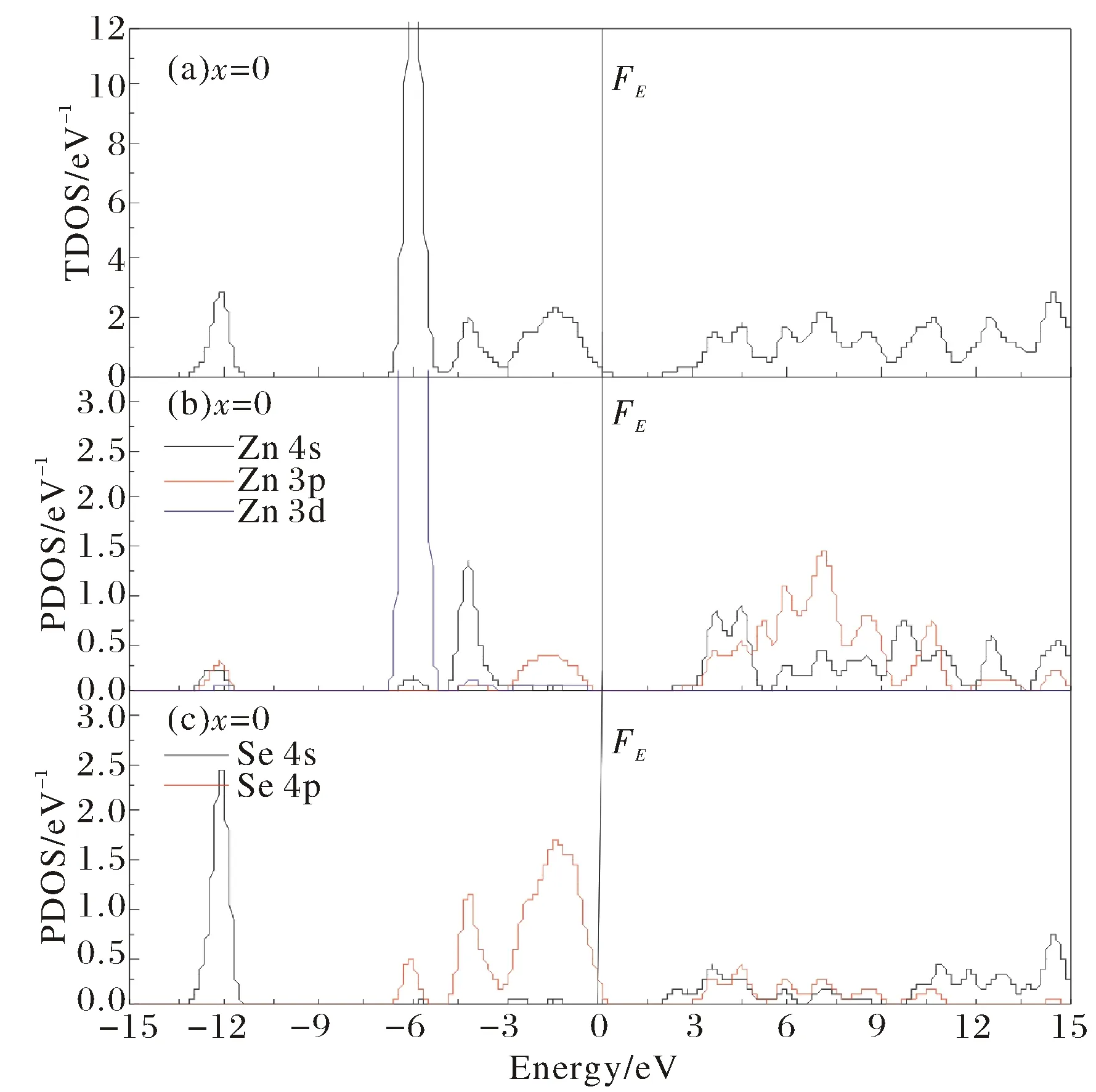
Fig.5 The TDOS and PDOS of ZnSe: (a) TDOS of ZnSe; (b) PDOS of Zn atom; (c) PDOS of Se atom

The TDOS and PDOS of MgxZn1-xSe alloys are shown in Fig.6～Fig.8， respectively. It is clear that the CBM along theΓ-Γpath that above the Fermi surface is mainly contributed by the Zn 4s states， Zn 3p states and Mg 2p states， while the VBM along theΓ-Γdirection that near the Fermi surface is primarily determined by the S 3p states in MgxZn1-xSe alloys. In particular， compared with the band structure of zinc-blende ZnSe， the CBM along theΓ-Γdirection shifts upwards higher energy region with the increasing Mg dopant compositionxin MgxZn1-xSe alloys， which is mainly resulted from the s-s type exchange interaction relates to Mg 2s states with Zn 4s and Se 4s states. Meanwhile， it is also observed that the VBM along theΓ-Γpath shifts downwards lower energy region with the increasing dopant compositionxin MgxZn1-xSe alloys， which relates to the reduction of p-d type exchange interaction due to the deficiency of 3p states for Mg as compared with Zn， and the increased p-p type exchange interaction derives from Mg 2p states with Zn 3p states， which results in the increase of band gap in MgxZn1-xSe alloys as shown in Fig.3．

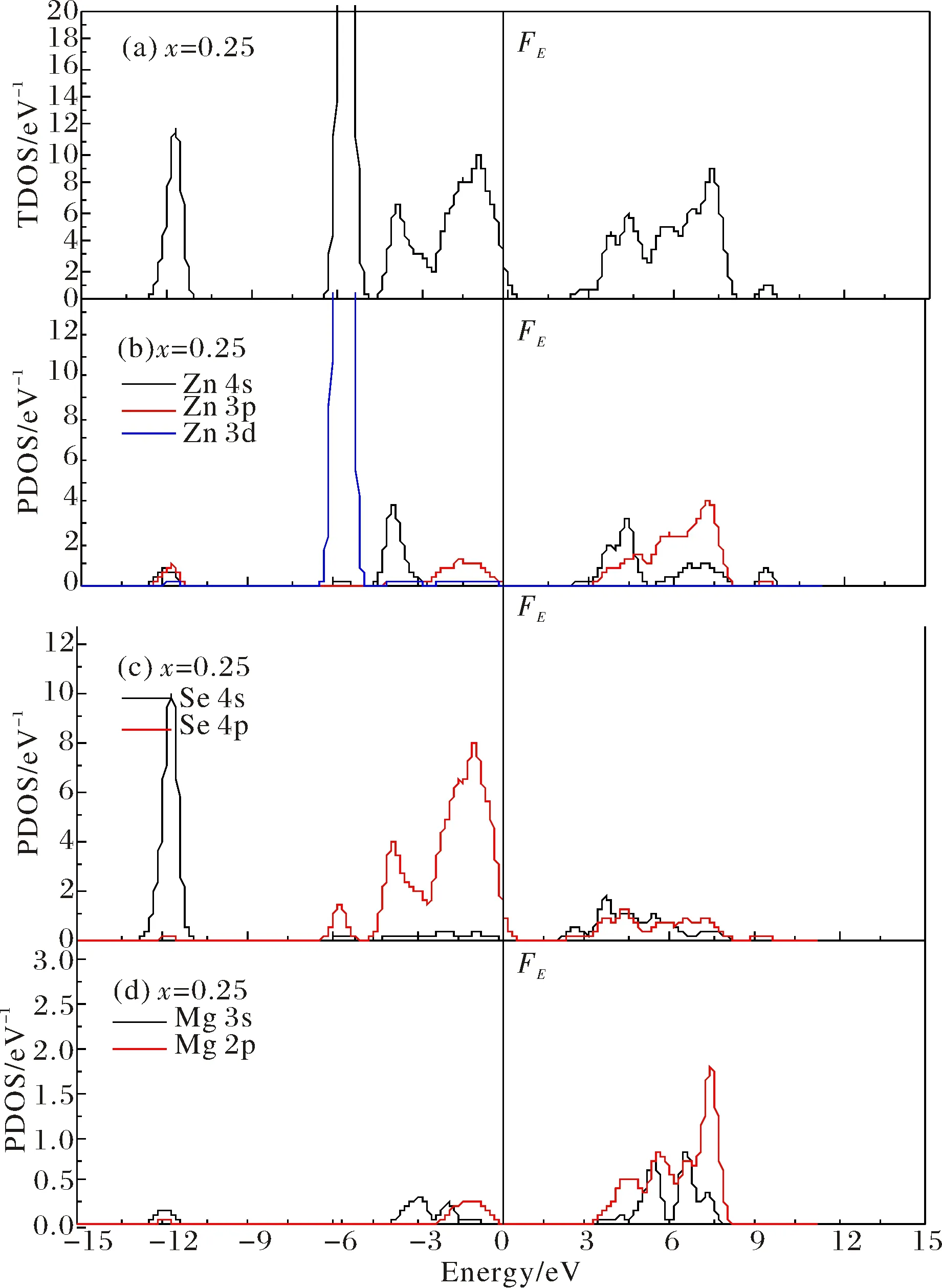
Fig.6 The TDOS and PDOS of Mg0.25Zn0.75Se (a)TDOS of Mg0.25Zn0.75Se; (b)PDOS of Zn atom; (c)PDOS of Se atom; (d)PDOS of Mg atom

Fig.7 The TDOS and PDOS of Mg0.50Zn0.50Se(a)TDOS of Mg0.50Zn0.50Se; (b)PDOS of Zn atom; (c)PDOS of Se atom; (d)PDOS of Mg atom

In particular， it is also found that the 3d states of Zn located around -4.5 eV are disintegrated into two parts， which relate to theegandt2gstates originated from Zn 3d states. Moreover， the crystal field splitting of energyE=Et2g-Eegfor MgxZn1-xSe alloys increases with an increase in Mg dopant compositionx. This can be explicated by the Jahn-Teller effect， where crystal distortion due to the larger size of Mg atoms， which also implies the results that the Mg0.25Zn0.75Se may be the most stable in the MgxZn1-xSe alloys．

Fig.8 The TDOS and PDOS of Mg0.75Zn0.25Se: (a)TDOS of Mg0.75Zn0.25Se; (b)PDOS of Zn atom;(c)PDOS of Se atom; (d)PDOS of Mg atom

2.3 Optical properties

In order to determine the optical properties of MgxZn1-xSe alloys， the complex dielectric function and optical absorption coefficient of MgxZn1-xSe alloys have been calculated. Both the complex dielectric function and optical absorption coefficient are directly relevant to the electronic structure. The real part and imaginary part of complex dielectric function， and the optical absorption coefficient obey the following formulations as

ε(ω)=ε1(ω)+iε2(ω)，

(2)

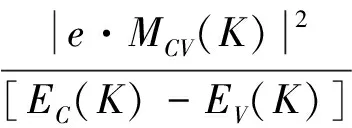
(3)

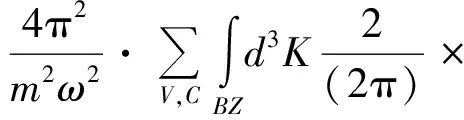
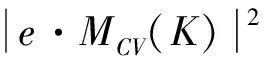
δ[EC(K)-EV(K)-ћω]，

(4)

(5)

whereωis the frequency of incident photon，αωis the optical absorption coefficient.ε1ωandε2ωare the real part and imaginary part of complex dielectric functionεω， respectively. The imaginary partε2ωis directly relevant to the band structure and the real partε1ωcan be obtained by Kramers-Kronig relationship.

The real partε1ωand imaginary partε2ωof complex dielectric functionεωfor MgxZn1-xSe alloys are presented in Fig.9～Fig.10， respectively. As shown in Fig.9， the first dielectric absorption peaks of real partε1ωdecrease and the dielectric absorption sides of MgxZn1-xSe alloys shift upwards higher photon energy region with the increases of Mg dopant concentration. Meanwhile， the static dielectric constant at the zero frequency limitε10 of MgxZn1-xSe alloys decreases from 8.11 to 4.85 with dopant composition x increases from 0 to 0.75， which induces an increase of band gap for MgxZn1-xSe alloys in Fig.3. In order to elucidate the dependence between the static dielectric constant and band gap for MgxZn1-xSe alloys， the theoretical model[17]ε1(0)≈1+(ћω′/Eg)2has been given， where ћ is the Dirac constant，ω′ is the plasma frequency and Egis the band gap of MgxZn1-xSe alloys. It clearly indicates the inverse proportion relation between the static dielectric constant and band gap of MgxZn1-xSe alloys.

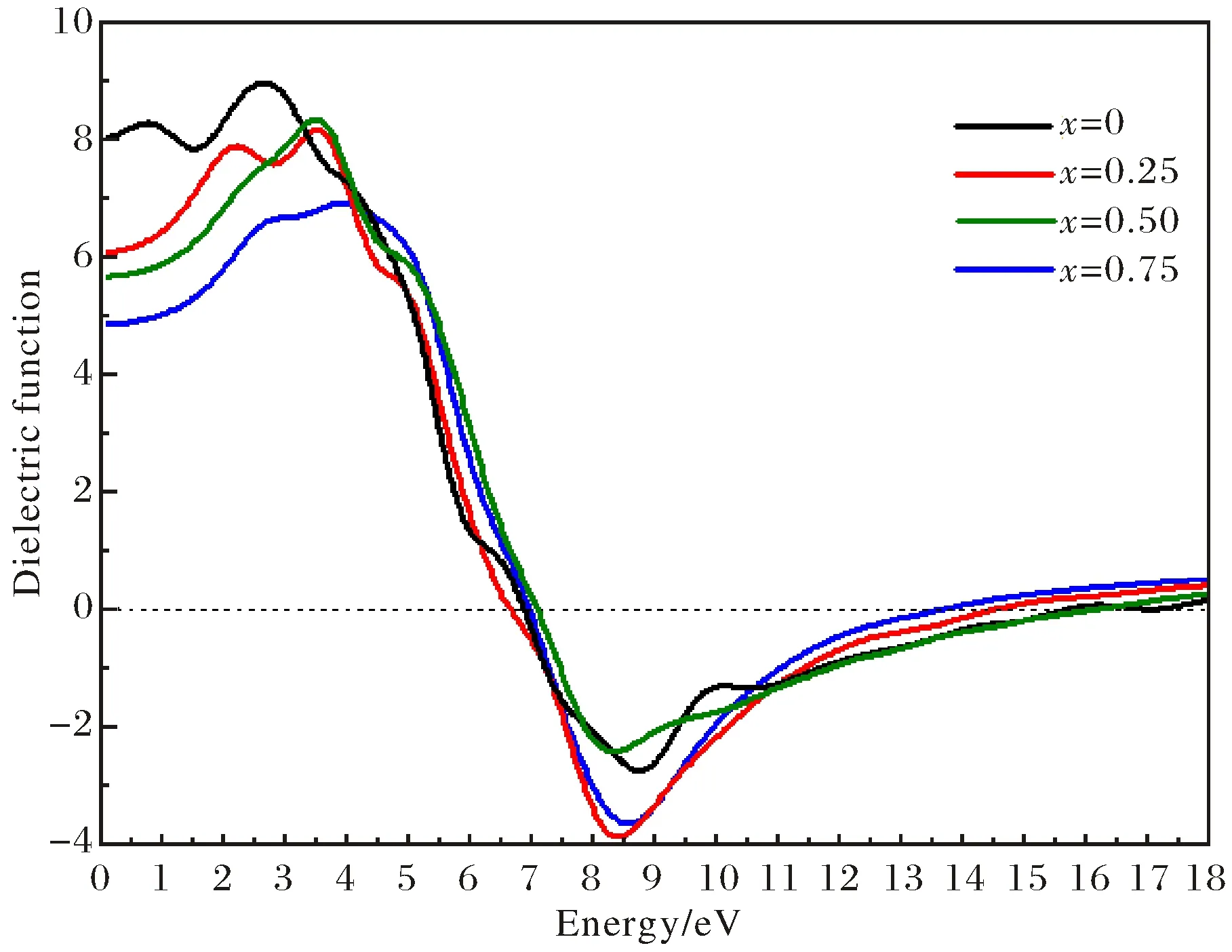
Fig.9 Dielectric function of real part for MgxZn1-xSe alloys

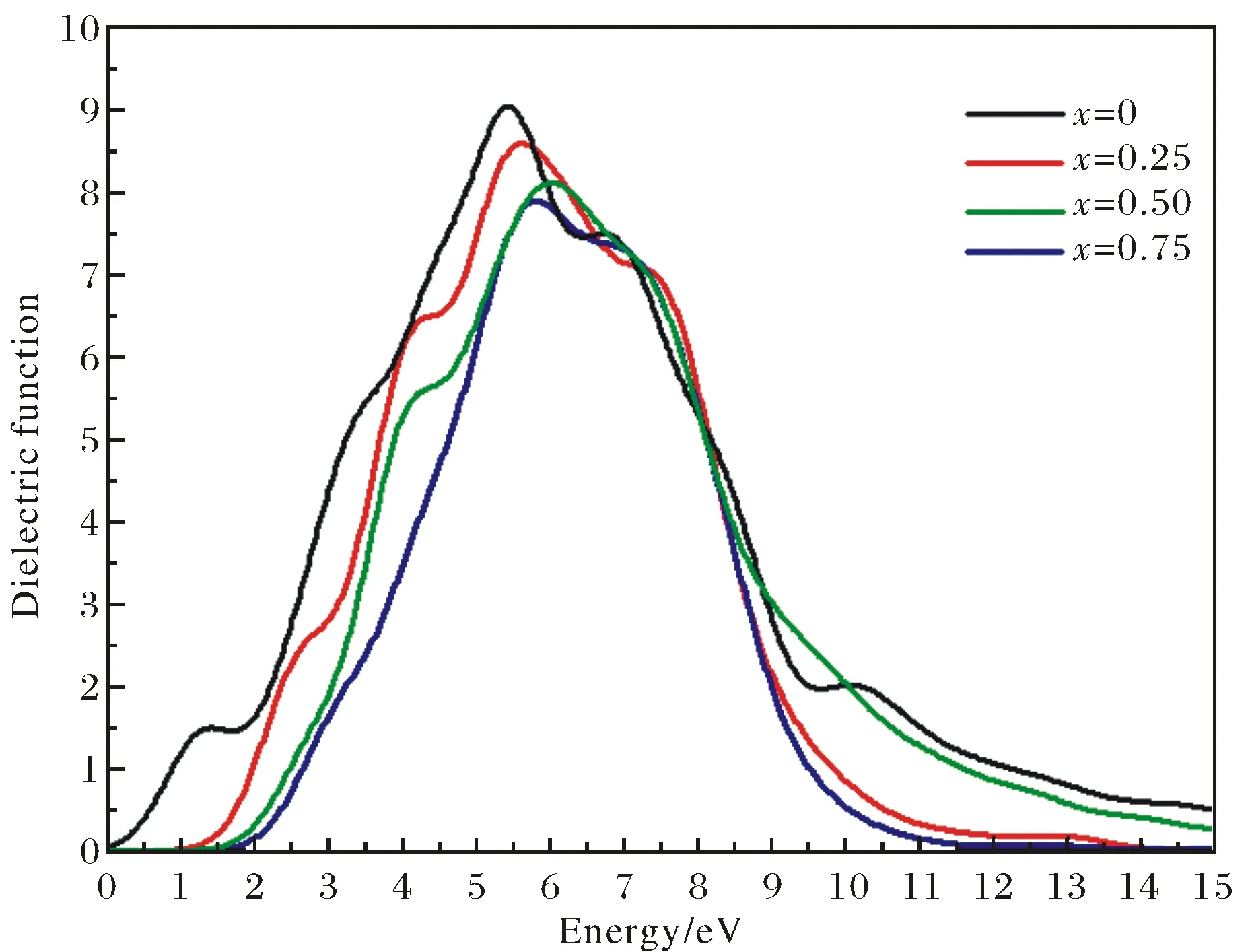
Fig.10 Dielectric function of imaginary part for MgxZn1-xSe alloys

Fig.10 shows the imaginary partε2ωof complex dielectric functionεωfor MgxZn1-xSe alloys. It is clear that the imaginary partε2ωof MgxZn1-xSe alloys shows a strong dielectric absorption region corresponds to incident photon energy ranges from 2 eV to 11 eV. In particular， the sharp dielectric absorption peaks inε2ωare observed at around 5.5 eV and 7.2 eV， which are mainly contributed by the electronic transition of Se 4p states with Zn 4s and Zn 3p states. The initial critical points of imaginary partε2ωfor MgxZn1-xSe alloys have been found at around 0.05 eV， 0.33 eV， 0.47 eV and 0.78 eV respectively， which also are considered as the threshold energy of the direct optical transitions for MgxZn1-xSe alloys occurring at 1.30 eV， 1.66 eV， 1.94 eV and 2.30 eV correspond to Mg dopant compositionxat 0， 0.25， 0.50 and 0.75， respectively. Moreover， it is observed that the first dielectric peaks of imaginary partε2ωoccur at around 5.5 eV decrease and the dielectric absorption peaks of imaginary partε2ωshift towards higher photon energy region with increasing Mg dopant composition， which validates the results that the band gaps of MgxZn1-xSe alloys increase with the increases of Mg dopant concentration in Fig.3．

Fig.11 shows the optical absorption spectrum of MgxZn1-xSe alloys. It is observed that the optical absorption curves of MgxZn1-xSe alloys are mainly displayed in the ultraviolet light region corresponds to photon wavelength ranges from 50 nm to 400 nm and the absorption coefficient maximum of MgxZn1-xSe alloys is higher than 2.5×105cm-1， which indicates the unique ultraviolet absorption properties and show an important potential applications prospects for MgxZn1-xSe alloys in ultraviolet detectors. The similar ultraviolet absorption spectrum has also been reported experimentally by Archana et al[14]. In particular， the optical absorption peaks maximum of MgxZn1-xSe alloys have improved as compared with the pure ZnSe， and the strongest absorption peaks have been displayed in Mg0.25Zn0.75Se alloys. Meanwhile， the optical absorption sides of MgxZn1-xSe alloys show a blue-shift obviously with the increases of Mg doping concentration， which derives from the interband transition between Se 4p and Zn 4s states， and it confirms the results that the increase of band gaps for MgxZn1-xSe alloys with the increases of Mg dopant composition as shown in Fig.3.

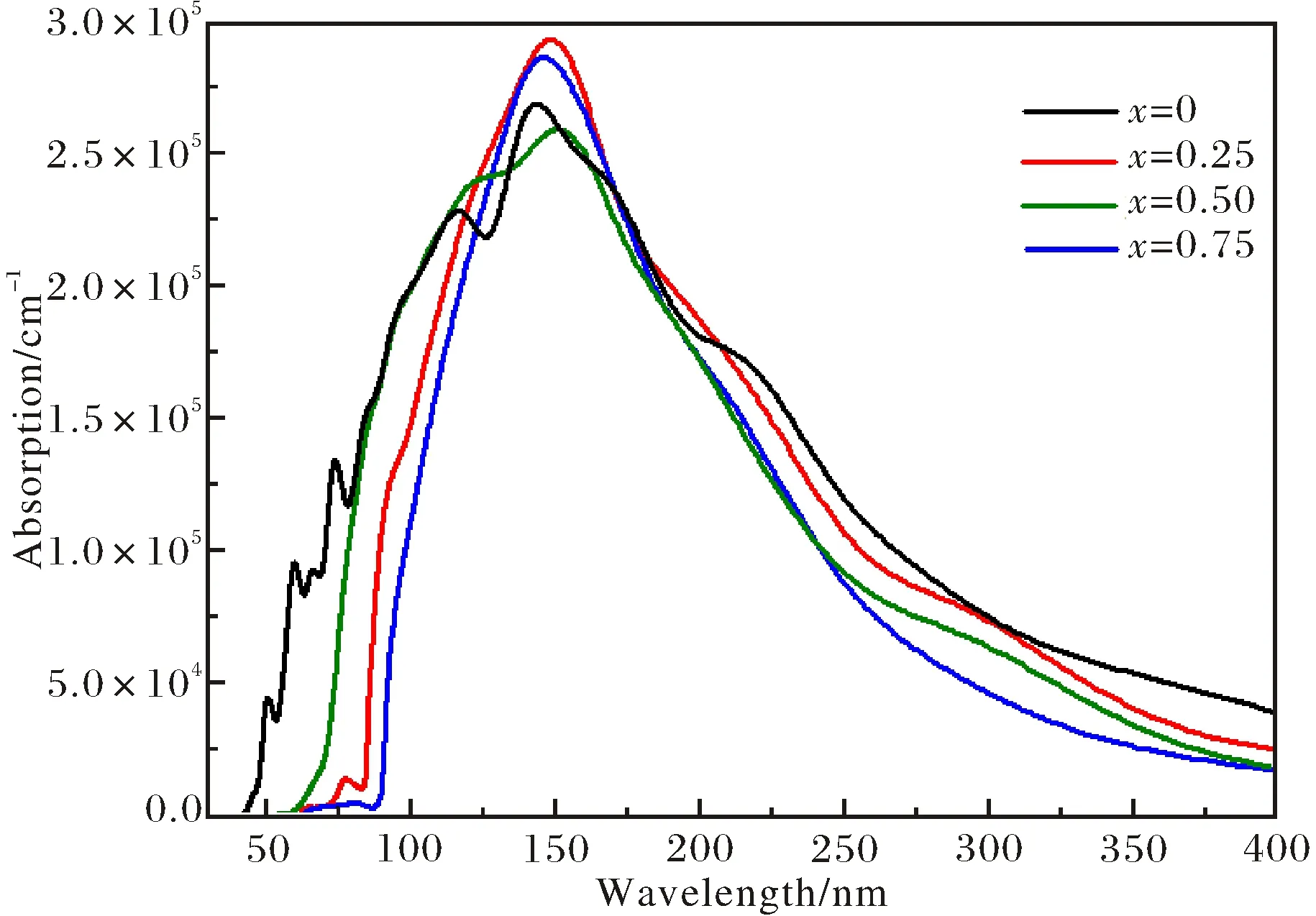
Fig.11 Optical absorption spectrum of MgxZn1-xSe alloys

3 Conclusion

In this paper， we have reported the band structure， density of states and optical properties of zinc-blende MgxZn1-xSe alloys from first-principles calculations based on the density functional theory. The calculated results indicate that both the pure and Mg-doped ZnSe alloys display a direct band structure and the band gap increases from 1.30 eV to 2.30 eV with the increases of Mg dopant compositionxranges from 0 to 0.75. In particular， the band gap of MgxZn1-xSe alloys can be evaluated by the first order functionEg=1.30+1.34xwith compositionxranges from 0 to 0.75. The upper valence band is mainly dominated by the Se 4p and Zn 3p states， while the lower conduction band is primarily contributed by the Zn 4s， Zn 3p and Se 4s states in MgxZn1-xSe alloys. Moreover， the static dielectric constant decreases and the optical absorption spectrum shows a blue-shift obviously in MgxZn1-xSe alloys. The results provide useful theoretical guidance for the potential applications of MgxZn1-xSe alloys in optical detectors.

[1] HAASE M A， QUI J， DEPUYDT J M， et al. Blue-green laser diodes [J]. Appl Phys Lett， 1991，59: 1272-1274．

[2] JEON H， DING J， XIE A V N， et al. ZnSe based multilayer pn junctions as efficient light emitting diodes for display Applications [J]. Appl Phys Lett， 1992，60: 892-894．

[3] COE S， STECKEL J S， KIM L， et al. Electroluminescence from single monolayers of nanocrystals in molecular organic devices [J]. Nature， 2002，420: 800-803．

[4] XIE W， GRILLO D C， GUNSHOR R L， et al. Blue/green pn junction electroluminescence from ZnSe-based multiple quantumwell structures [J]. Appl Phys Lett， 1992，60: 463-465．

[5] HE Y， LU H T， SAI L M， et al. Microwave synthesis of water-dispersed CdTe/CdS/ZnS core-shell-shell quantum dots with excellent photostability and biocompatibility [J]. Advanced Materials， 2008，20: 3416-3421．

[6] WOOD V， HALPERT J E， PANZER M J， et al. Alternating current driven electroluminescence from ZnSe/ZnS∶Mn/ZnS nanocrystals [J]. Nano Letters， 2009，9: 2367-2371．

[7] ZHANG Y， HU C G， FENG B， et al. Synthesis and photocatalytic property of ZnSe flowerlike hierarchical structure [J]. Applied Surface Science， 2011，257: 10679-10685．

[8] CHENG D C， HAO H C， ZhANG M， et al. Improving Si solar cell performance using Mn∶ZnSe quantum dot-doped PLMA thin film [J]. Nanoscale Research Letters， 2013，8: 291(1-5)．

[9] KARAZHANOV S Z， RAVINDRAN P， KJEKSHUS A， et al. Electronic structure and optical properties of ZnX (X=O， S， Se， Te): a density functional study [J]. Phys Rev B， 2007，75: 155104(1-14)．

[10] ZHANG X J， WANG D D， BERES M， et al. Zincblende-wurtzite phase transformation of ZnSe films by pulsed laser deposition with nitrogen doping [J]. Appl Phys Lett， 2013，103: 082111(1-3)．

[11] AMIN B， AHMAD I， MAQBOOL M， et al. Ab initio study of the bandgap engineering of Al1-xGaxN for optoelectronic applications [J]. J Appl Phys， 2011，109: 023109(1-5).

[12] ARCHANA J， NAVANEETHAN M， PRAKASH T， et al. Chemical synthesis and functional properties of magnesium doped ZnSe nanoparticle [J]. Materials Letters， 2013，100: 54-57．

[13] CAR R， PARRINELLO M. Unified approach for molecular dynamics and density-functional theory [J]. Phys Rev Lett， 1985，55: 2471-2474．

[14] WU Z G， COHEN R E. More accurate generalized gradient approximation for solids [J]. Phys Rev B， 2006，73: 235116(1-6)．

[15] KARZEL H， POTZEL W， KOFFERLEIN M， et al. Lattice dynamics and hyperfine interactions in ZnO and ZnSe at high external pressures [J]. Phys Rev B， 1996，53: 11425-11438．

[16] OLEG Z， ANGEL R， BLASE X， et al. Quasiparticle band structures of six II-VI compounds: ZnS， ZnSe， ZnTe， CdS， CdSe， and CdTe [J]. Phys Rev B， 1994，50: 10780-10787．

[17] PENN D R. Wave-number-dependent dielectric function of semiconductors [J]. Phys Rev， 1962，128: 2093-2097．

2017-05-21.

湖北省自然科学基金项目(2015CFC784)．

1000-1190(2017)06-0796-08

MgxZn1-xSe合金的电子结构、光学性质和稳定性的第一性原理研究

余志强1，2， 张昌华1， 廖红华1， 李时东1， 郎建勋1

(1.湖北民族学院 电气工程系， 湖北 恩施 445000; 2.华中科技大学 光学与电子信息学院， 武汉 430074)

基于密度泛函理论的第一性原理计算，研究了闪锌矿MgxZn1-xSe合金的稳定性、电子结构和光学性质.研究结果表明，闪锌矿ZnSe和MgxZn1-xSe合金都为直接带隙半导体，MgxZn1-xSe合金的带隙宽度Eg和形成能Eb分别可以由Eg=1.30+1.34x和Eb=-1.48+0.60x-0.27x2进行估计.同时，MgxZn1-xSe合金的价带顶主要取决于Se 4p 和 Zn 3p态电子的相互作用，而其导带底则主要由Zn 4s、Zn 3p 以及Se 4s态电子共同决定.此外，随着镁掺杂系数x的逐渐增大，MgxZn1-xSe合金的静态介电常数逐渐减小，而其吸收谱则出现明显的蓝移现象.研究结果为MgxZn1-xSe合金在光电探测器方面的应用提供了重要的理论指导.

第一性原理; MgxZn1-xSe合金; 电子结构; 光学性质

O481.1

A

*通讯联系人. E-mail: zhiqiangyu@hust.edu.cn; zch-tan@tom.com．

10.19603/j.cnki.c