基于个人投资视角反观房地产市场的宏观调控

吴 迪， 郭思培， 何 穗

(华中师范大学 数学与统计学学院， 武汉 430079 )

基于个人投资视角反观房地产市场的宏观调控

吴 迪*， 郭思培， 何 穗

(华中师范大学 数学与统计学学院， 武汉 430079 )

对我国房地产市场进行实证分析，发现该市场具有分形特征以及房价与租金存在线性关系.在此前提下，应用实物期权理论对投资收益进行预估，建立个人房地产投资租转售决策分析模型.运用停时与数值模拟等方法求解，得到投资者执行租转售决策时的房价可行区间.继而定性分析房地产市场基本要素对房价可行区间产生的影响，得出了相关结论.最后利用模型结论对北京二手住宅房地产市场进行阶段性研究，反向剖析近年来政府对房地产市场所做的系列宏观调控政策.

房价； 分形特征； 实物期权； 停时； 分数布朗运动

近年来，我国城市发展迅猛，资源优厚，吸引了大批外来人口.据中国统计年鉴报告，1992年～2016年，我国城乡人口比例从37.85%快速增长到127.79%.逐年攀升的城市人口带来了对住宅的持续高需求.中国房地产业协会发布的房价行情显示，2017年2月北京房价收入比高达14.5.房价与居民收入的巨大差距凸显出房地产市场过热、价格过高、供求畸形.房地产投资的不可逆性隐藏着巨大的金融风险.如何抑制房价，实现城市高房价的软着陆成为了现阶段主要面临的经济难题.

本文将持有房产的投资者作为解决问题的着眼点，基于实物期权理论框架，建立个人房地产投资租转售决策分析模型.

1 文献回顾

实物期权的理论基础是金融期权定价理论(S.P.Mason和R.C.Merton)[1].金融期权的核心思想是在市场完备无套利的情况下复制期权，对期权进行定价.实物期权从本质上可看做是金融期权的推广应用.

传统的期权定价模型假设标的资产价格变化服从几何布朗运动，资产价格的对数增长率服从正态分布.Black和Scholes[2]提出了著名的Black-scholes期权定价模型.Ross和Cox[3]继而提出风险中性定价理论，进一步又提出离散情况下的二叉树定价模型.然而近年来对金融市场的大量研究表明，金融资产的对数收益率呈现出“尖峰厚尾”的特点，且价格之间存在着长程相关性.Peters[4]提出分形市场假说，分析了不同资本市场都存在着分形结构和非周期循环的存在.说明运用分形市场理论比有效市场假说更能准确地刻画市场特征.Necula[5]等人分析了分数布朗运动下的期权市场，并给出了欧式期权在任意时刻的期权定价公式.国内亦有黄文礼[6]、孙玉东[7]众多学者研究了分数布朗运动下的衍生品定价问题.

实物期权在房地产市场上的运用：起始于Titman[8]利用二叉树期权定价模型在离散条件下评估土地价格；Clark[9]等利用选择期权分析房地产开发密度；Geltner[10]等利用开发期权分析了房地产市场.之后Williams[11]、Capozza[12]等做了进一步的推广研究.国内研究房地产个人投资策略极少，主要有蔡晓钰等人[13]基于房价满足几何布朗运动的假设下对投资住房的售出问题进行建模分析研究，并在后期进一步考察了租转售问题[14][15].韩露[16]基于二叉树模型考察实物期权在房地产投资时机决策中的应用.

需要注意的是，关于实物期权在房地产市场上的应用大多是建立在房地产市场为有效市场的前提下进行的理论研究，即房价满足几何布朗运动.而谭峻等[17]证明了中国大陆房地产市场波动具有分性特征.本文沿此思路，在实证研究我国房地产市场特征的前提下，建立个人房地产投资租转售决策分析模型.依据模型求解结果来反〗向剖析政府对房地产市场的宏观调控，亦揭示了政府可以利用房地产市场发展数据来对模型相关参量做出估计，针对性地做出合理的调控政策.

2 房地产市场特征检验

2.1 房地产市场分形特征检验

本文选取1991年2月～2017年3月的中国房地产市场交易的月度数据(数据来源：国家统计局)，运用去趋势波动分析(DFA) 方法(张卫国等)[18]估计中国房地产市场的Hurst 指数.其拟和函数图像如图1所示.

由于Hurst的估计值为0.72(远大于0.5)，故房价对数增长率时间序列具有长程相关性，说明房

地产市场历史的价格波动对现在的价格增量具有正效应.即中国房地产市场是分形市场，用几何分数布朗运动来刻画房价来建模是合理的.

图1 房价对数增长率Hurst指数Fig.1 Hurst exponent of the logarithmic growth rate of house prices

2.2 房价租金比实证检验

在理想的市场环境下，房价租金比为定值(祈兆珍)[19].本文选取我国2002年12月～2017 年3 月的住房租金价格指数与住房价格指数的月度数据(数据来源：Resset 数据库)，其对数增长率走势如图2所示.

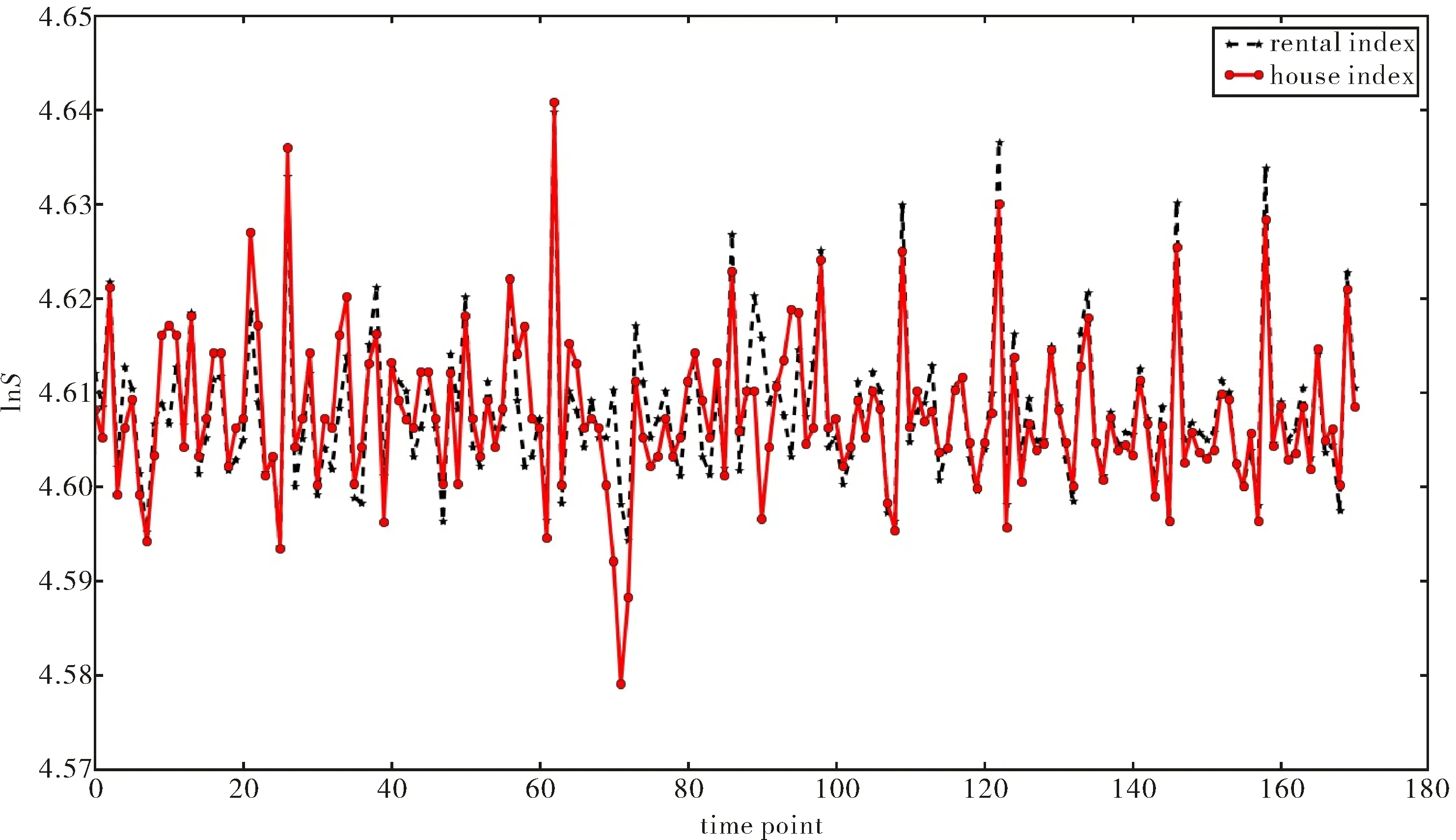
图2 住房和租金价格指数对数收益率走势图Fig.2 Trend of the logarithmic growth rate of prices of house and rent

可发现住房价格指数对数增长率与租金价格指数对数增长率走势基本相同.线性回归结果如表1所示，线性回归T检验的概率p值均为“***”，表示极为显著，且拟合优度为0.723 2，线性回归方程为y=0.82481x+0.8075，该线性模型通过回归检验.得出结论：在房地产市场建模中，假定房价与租金具有良好的线性关系是合理的.

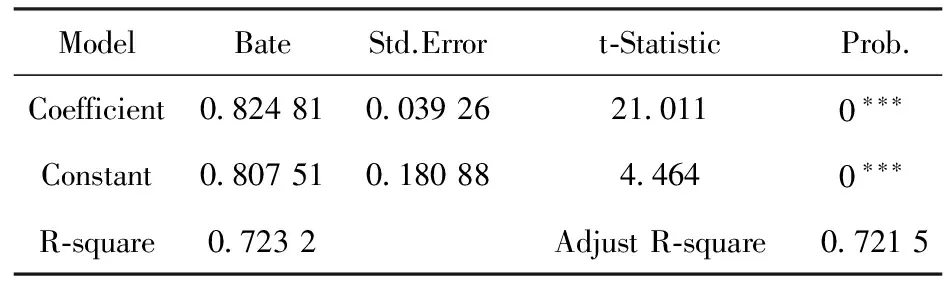
表1 回归结果

注：***表示检验在0.1%的水平上显著，**表示检验在1%的水平上显著，*表示检验在5%的水平上显著.

3 个人房地产投资租转售决策分析模型

3.1 基本假设

假设1：在房地产交易市场，购买→ 出租→ 出售都是通过中介机构，其交易是瞬时发生的，且不存在套利情况；

假设2：出租与租转售的交易成本与相应的交易价格成定比，分别记为θ1(0≤θ1≤1)，θ2(0≤θ2≤1)，其中出租的交易成本只包含支付给中介机构的佣金，租转售的交易成本包含中介佣金和相关税费；

假设3：投资者为理性投资者，在起始时刻0以价格P0购买一处房产，从而拥有出售期权，终止时刻为T，投资者可在T之前的任意时刻做出继续或停止决策，目的在于获得最大投资收益；

假设4：房价服从几何分数布朗运动，去膨胀化的房价期望增长率与波动率始终为定值，记为dP=μPdt+σPdBH(0≤t≤T)，BH为标准分数布朗运动，BH(0)=0，t时刻的的房价为Pt；

假设5：房价与租金呈线性关系，记为Rt=λPt+c0(0≤t≤T)， 其中λ，c0为定值；

假设7：无风险利率(贴现率)始终为定值r.

3.2 模型建立

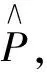
1) 若截止时刻T，投资者始终未执行租转售期权，即通过房屋出租实现房屋价值，亦是执行期权继续决策的价值，记为VT：

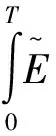
(1)

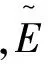
2) 若在时刻τ(0≤τ≤T)，投资者执行租转售期权的停止决策，则房屋价值即是停止决策的价值，记为Vτ：

(2)

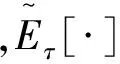
θ1(λPt+c0))e-rtdt≥0，

此不等式的解即为执行停止决策的房价可行域.

3.3 模型求解

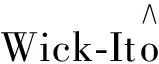
0≤t≤T,

(3)

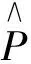
(4)

1)化简求解VT.

将式(5)代入式(4)，得

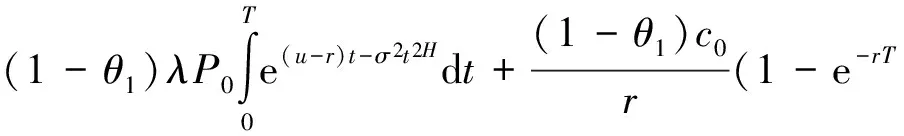
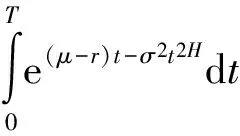
将T看做变值，采用数值算法，拟合ξ与T之间的代数关系，具体算法如下：

a) 参数的取值.

T：取初始值为0.001且在[0，1]之间间隔为0.001的等差数列，依次赋值给T；

μ-r：生成服从均匀分布U[0，1]的随机数50 000个，从中随机抽取1 000个，依次赋值给μ-r；

σ2：生成服从均匀分布U[0，0.25]的随机数50 000个，从中随机抽取1 000个，依次赋值给σ2；

2H：生成服从均匀分布U[1，2]的随机数50 000个，从中随机抽取1 000个，依次赋值给2H；

b) 根据

(5)

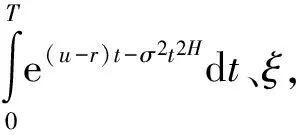
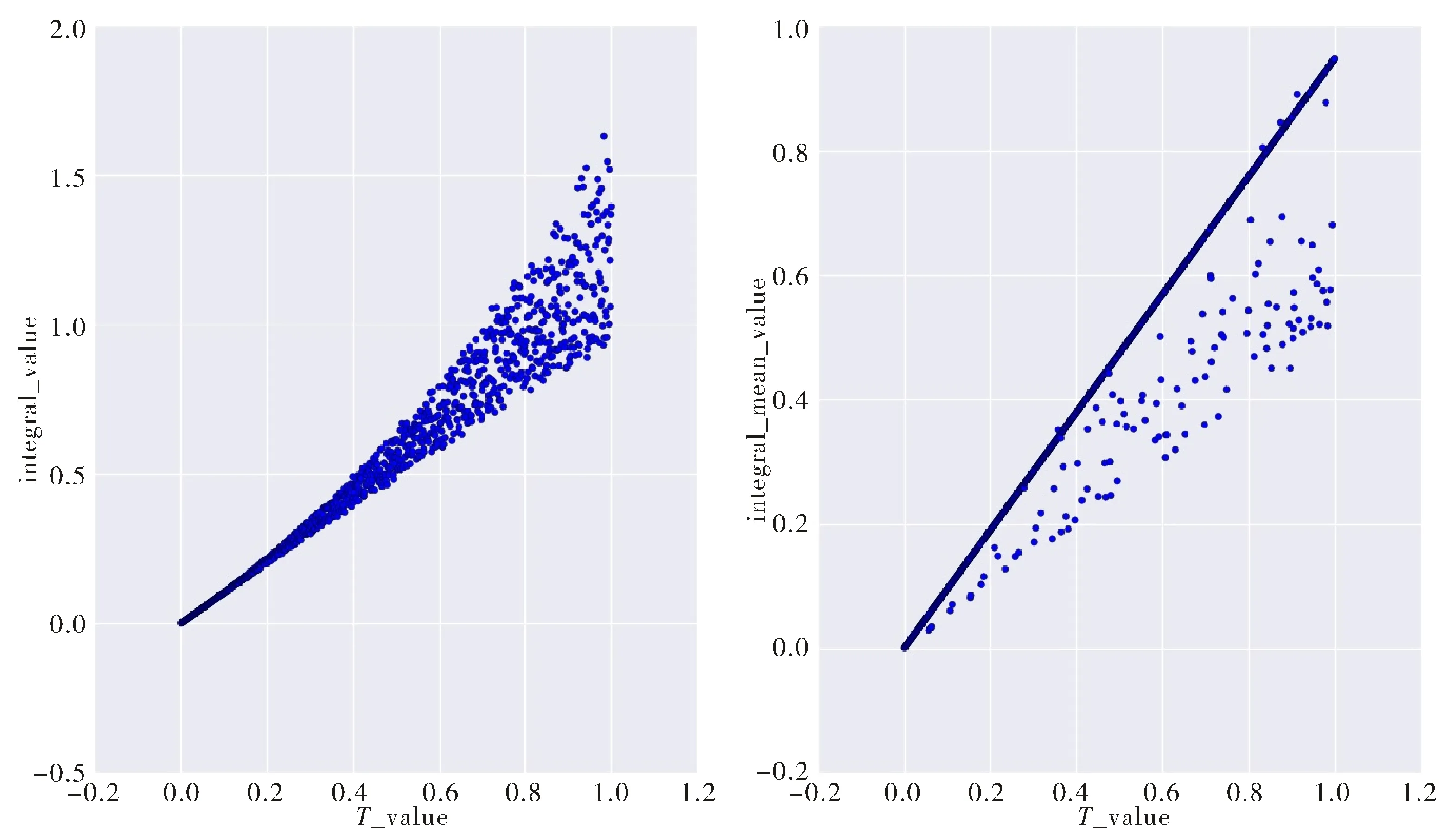
图3 散点图Fig.3 The scatter plot

c) 对ξ与T的散点分布进行线性回归分析，回归曲线如图4所示，回归结果如表2所示．

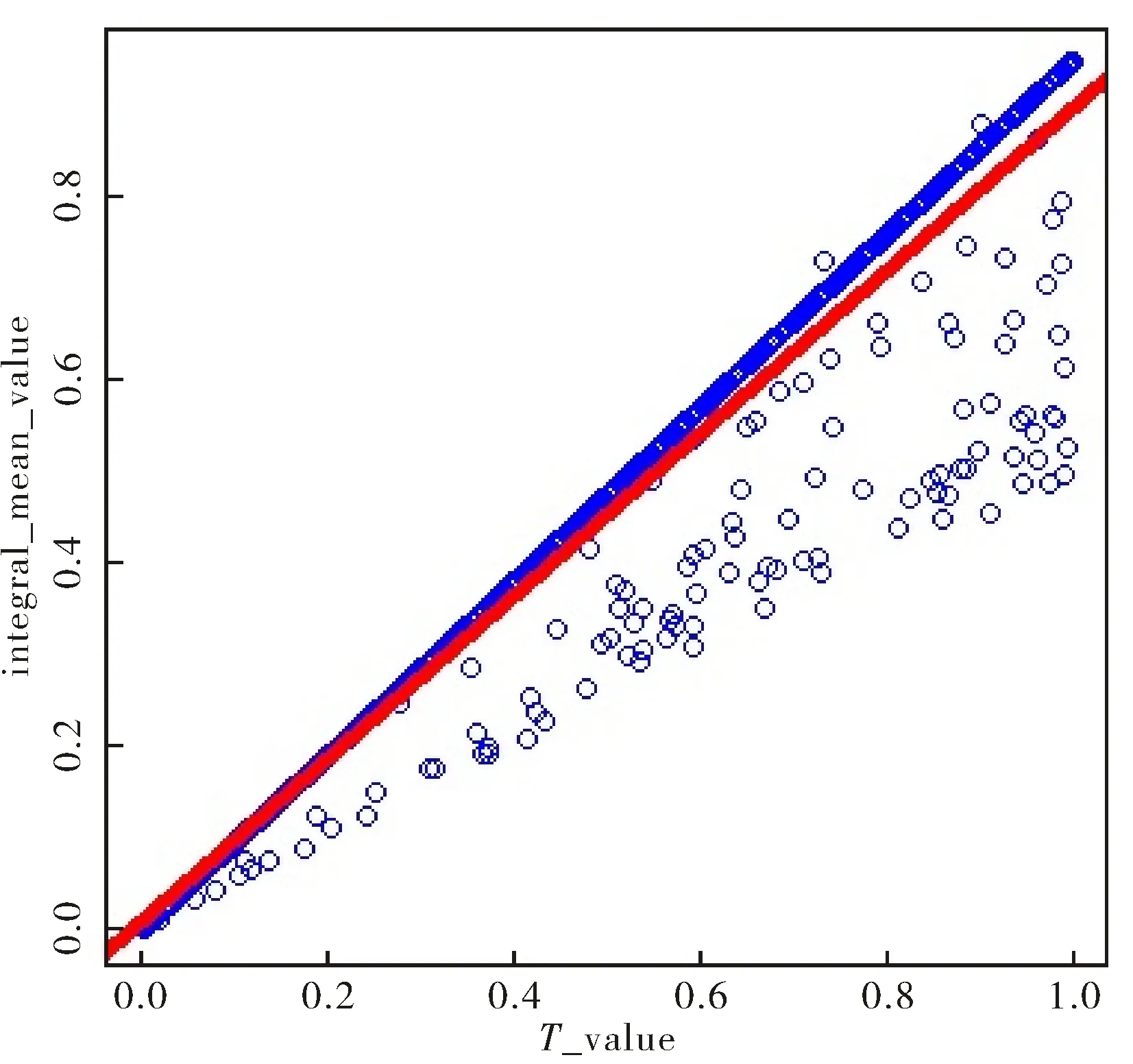
图4 T与ξ线性回归拟合曲线Fig.4 Linear regression fitting curve between T and ξ

ModelBateStd．Errort⁃StatisticProb．Coefficient08847410007514111740∗∗∗Constant0010160000434223400195∗R⁃square09328AdjustR⁃square09328

注：***表示检验在0.1%的水平上显著，**表示检验在1%的水平上显著，*表示检验在5%的水平上显著.

由于常数项对应的T检验的概率P值为“*”，即在1%的置信水平下不显著， 由此可得

ξ=0.884741T.

(6)

那么，当T取为某一定值时，ξ=0.884741T依然成立.为表述方便，不妨令k1=0.884741，所以

VT=(1-θ1)λP0Texp[(μ-r)k1T-

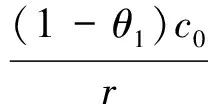
(7)

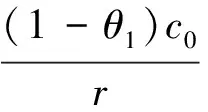
VT=(1-θ1)λP0Texp[(μ-r)k1T-

σ2(k1T)2H]+c(1-e-rT).

(8)

2) 化简求解Vτ.

将式(5)、(6)代入式(4)，并利用“1)”中的积分表示结果，得

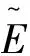
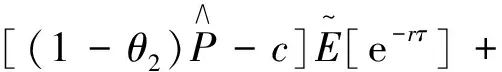
为求解Vτ，必须知晓基于几何分数布朗运动的停时τ的分布.对此，考虑任一满足假设条件的分数布朗运动，模拟出关于τ的分布的散点图，具体做法如下：

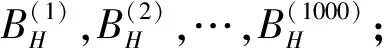
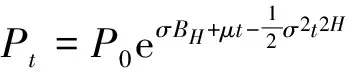
e) 由模拟路径的先后，作出关于停时τ的分布的散点图如图6所示．

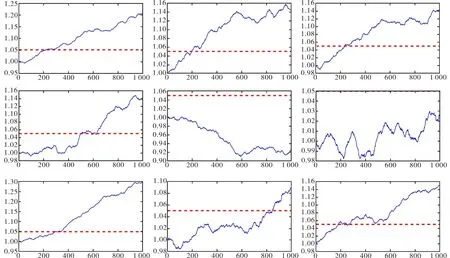
图5 路径的模拟Fig.5 The simulation of Pt routes

从模拟结果可以看出，基于房价满足几何分数布朗运动情况下的停时τ的分布规律为：靠近0的点较远离0的点更密集一些，可推测停时τ在风险中性测度下的的密度分布函数为单调递减函数.

为验证此结果，不失一般性，考察多时段二叉树模型.具体分析如下:

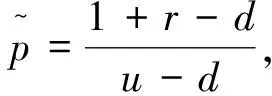
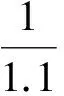
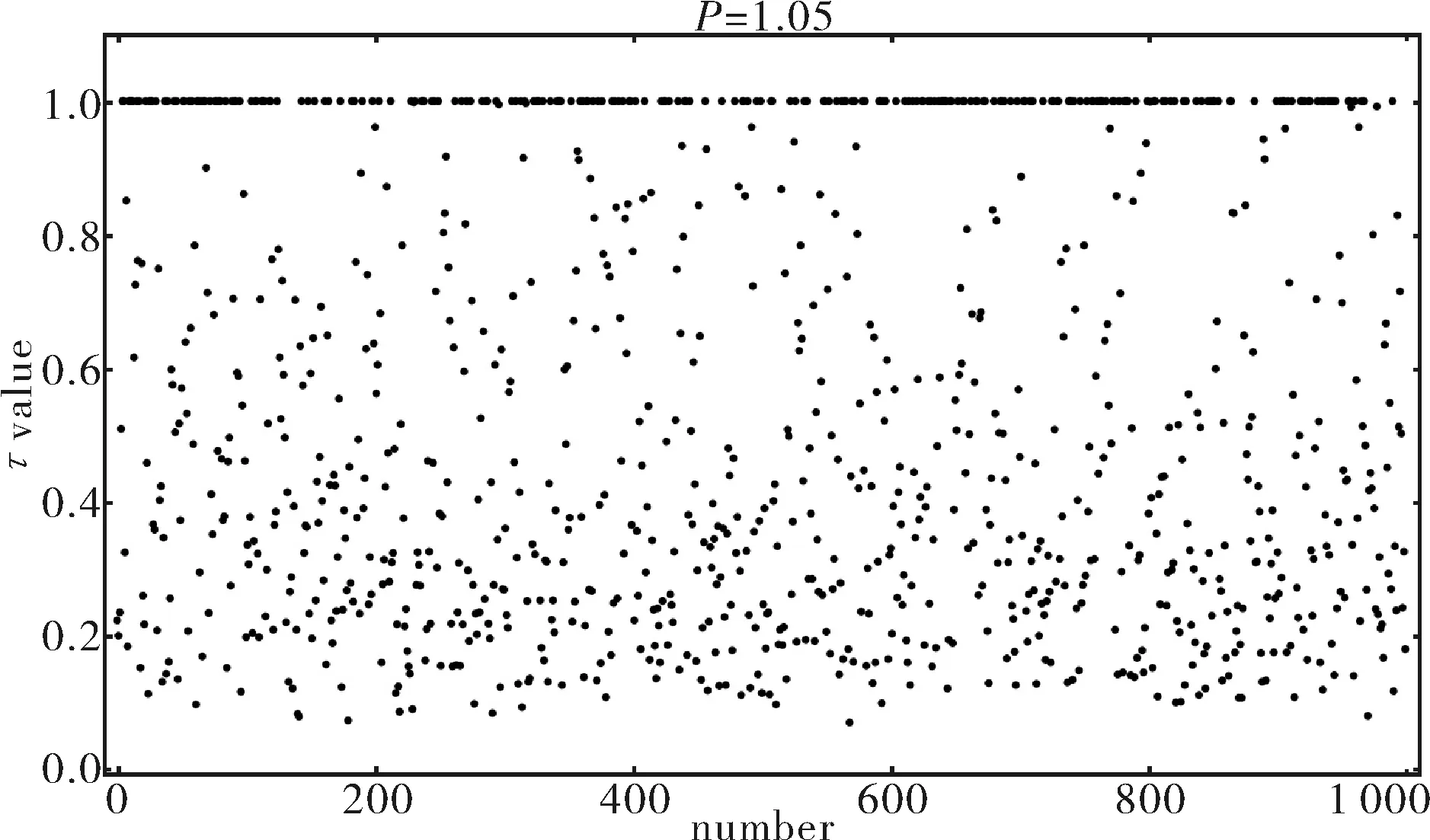
图6 停时τ的分布散点图Fig.6 The scatter plot of stopping time distribution τ

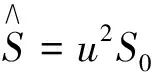
综上讨论，我们得出停时τ在风险中性测度下的密度分布函数为单调递减函数f(t)，为后续计算方便，不妨假定f(t)=e-t.所以

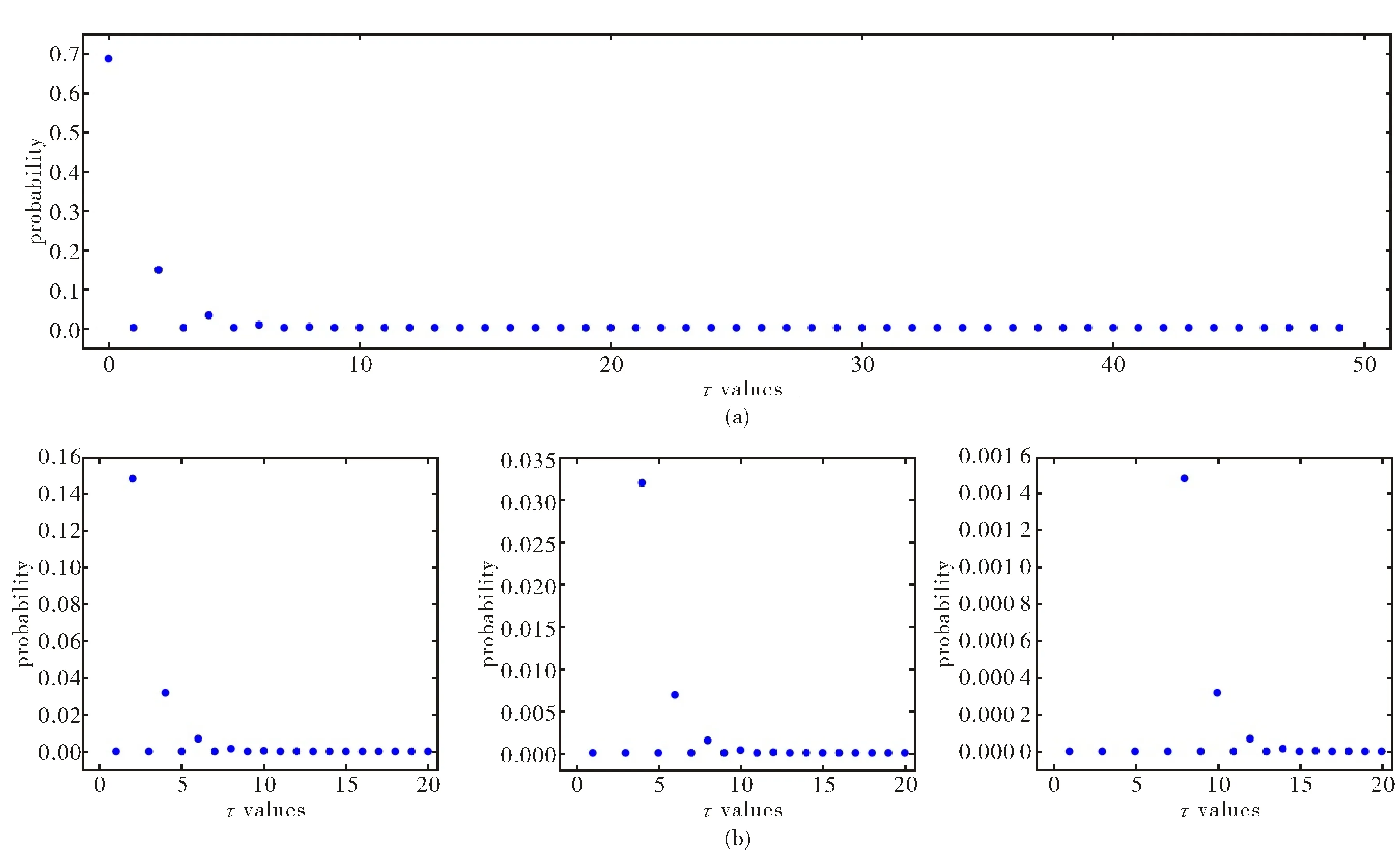
图7 二叉树模型下停时τ的分布散点图Fig.7 The scatter plot of stopping time τ distribution in model of a binary tree

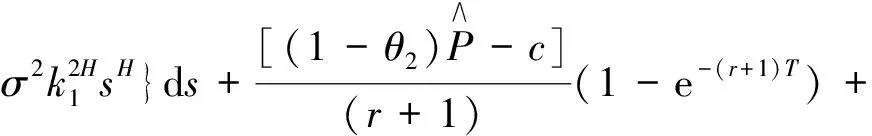
(9)

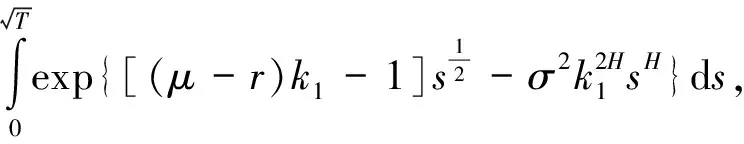
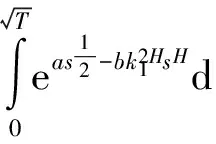
(10)

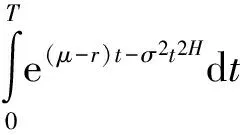
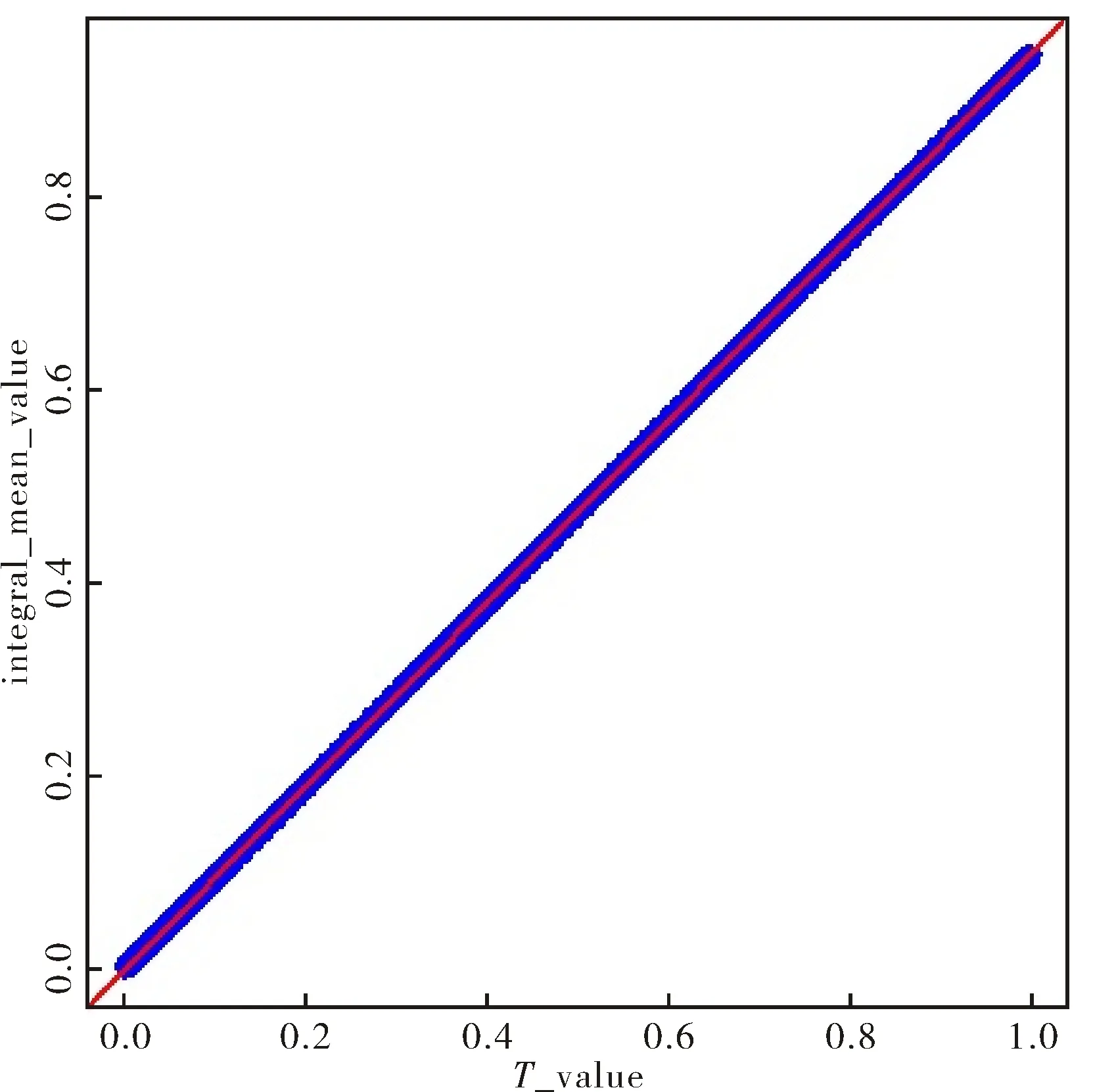
图8 线性回归拟合图Fig.8 Fitting figure of linear regression

ModelBateStd．Errort⁃StatisticProb．Coefficient9474e-013909e-102424e+090∗∗∗Constant5263e-061972e-102732e+040∗∗∗R⁃square1AdjustR⁃square1

注：***表示检验在0.1%的水平上显著，**表示检验在1%的水平上显著，*表示检验在5%的水平上显著.

类似讨论，由于常数项接近于0，可忽略不计，即得η=0.9474T，不妨令k2=0.9474.因此

推得,

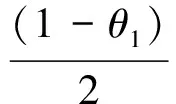
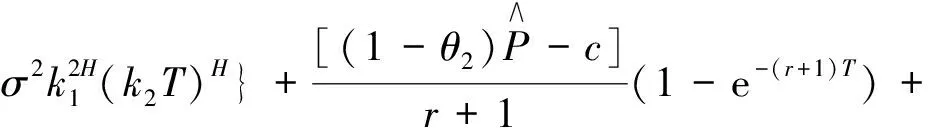
(11)

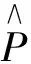
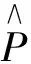
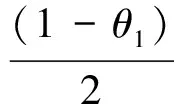
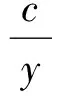
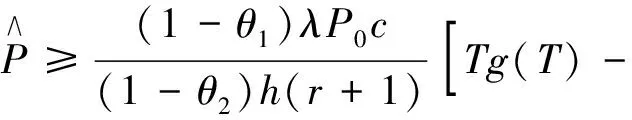
即停止决策的可行域为：

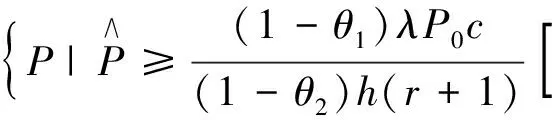
3.4 结果分析

定性分析各参数对可行域的影响，如图9所示．

具体的，记

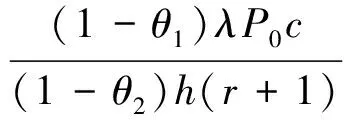
由于在参数未取定的情况下，无法确定g(x)的单调性，继而不能判断F(H，μ，σ，r，T)对相应参数求偏导之后的正负号，故此处运用数值试验来探讨F(H，μ，σ，r，T)与各参数之间的关系.

1) 考虑H对F(H，μ，σ，r，T)的影响

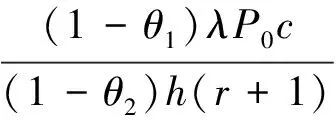
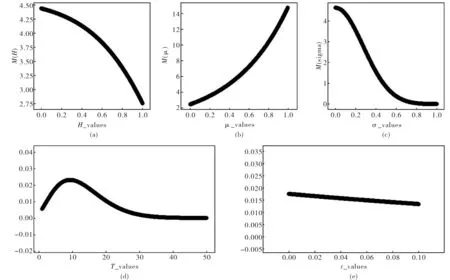
图9 参数(H，μ，σ，r，T)与的关系Fig.9 The relationship between parameters (H，μ，σ，r，T) and

2) 考虑μ对F(H，μ，σ，r，T)的影响

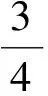
3) 考虑σ对F(H，μ，σ，r，T)的影响

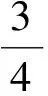
4) 考虑T对F(H，μ，σ，r，T)的影响

为讨论方便，设定c0=0，即房价租金比为定值.推得c=0，h(r)=0，此时，

F(H，μ，σ，r，T)=

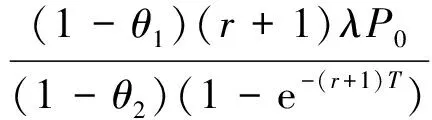
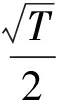
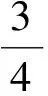
N(T)=

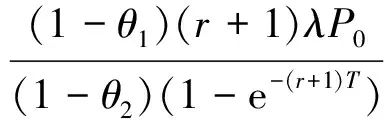
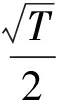
考察N(T)与T的关系即可，结果如图9(d)所示.可看到，投资期限的长短对临界值具有阶段性的影响，T∈[0，10]时，随着投资期限的短期延长，投资者执行停止决策的心理价位越来越高，且变化速度很快，对应于投资者执行停止决策的可行域越来越小，经过T=10这个节点之后，心理价位又急剧下降，最后持平，即对应于投资者执行停止决策的可行域越来越大，最后基本保持不变.显然，这与投资者的心态是紧密相关的，如果必须在短期内实现房屋价值，那么投资者必须要在短期内做出停止决策或继续决策，这就很可能出现要价高的情况.但进行长线投资时，即对时间没有要求，这时投资期限的延长初期会适当降低投资者执行停止决策的心理价位，但后期投资期限的延长对投资者执行停止决策的心理价位基本上不产生影响.

5) 考虑r对F(H，μ，σ，r，T)的影响

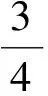
4 实证分析

以北京市为例，研究其二手住宅销售市场，截取2011 年1 月1 日～2017 年4 月30 日的二手住宅出售交易量的统计数据(数据来源：Wind资讯)，得到北京市二手住宅出售套数的走势如图10所示.

显然，北京市的二手房交易市场呈现出阶段性的特征，在2011年1月～2014年9月北京市的二手住宅交易市场处于低潮期，发展较为缓慢.2014年10月～2017年4月北京市的二手住宅交易市场空前活跃，处于兴盛期.以此，我们将北京市二手房交易市场分两阶段来考察并进行比较.分别记为第一时期、第二时期.从个人房地产投资角度来看，投资者选择在第二时期执行停止决策的人数明显要多于第一时期，说明在第二时期内房地产市场投资者的心理价位的下确界要低于第一时期，以下将通过两时段的北京房地产市场价格相关参数比较来进行分析.

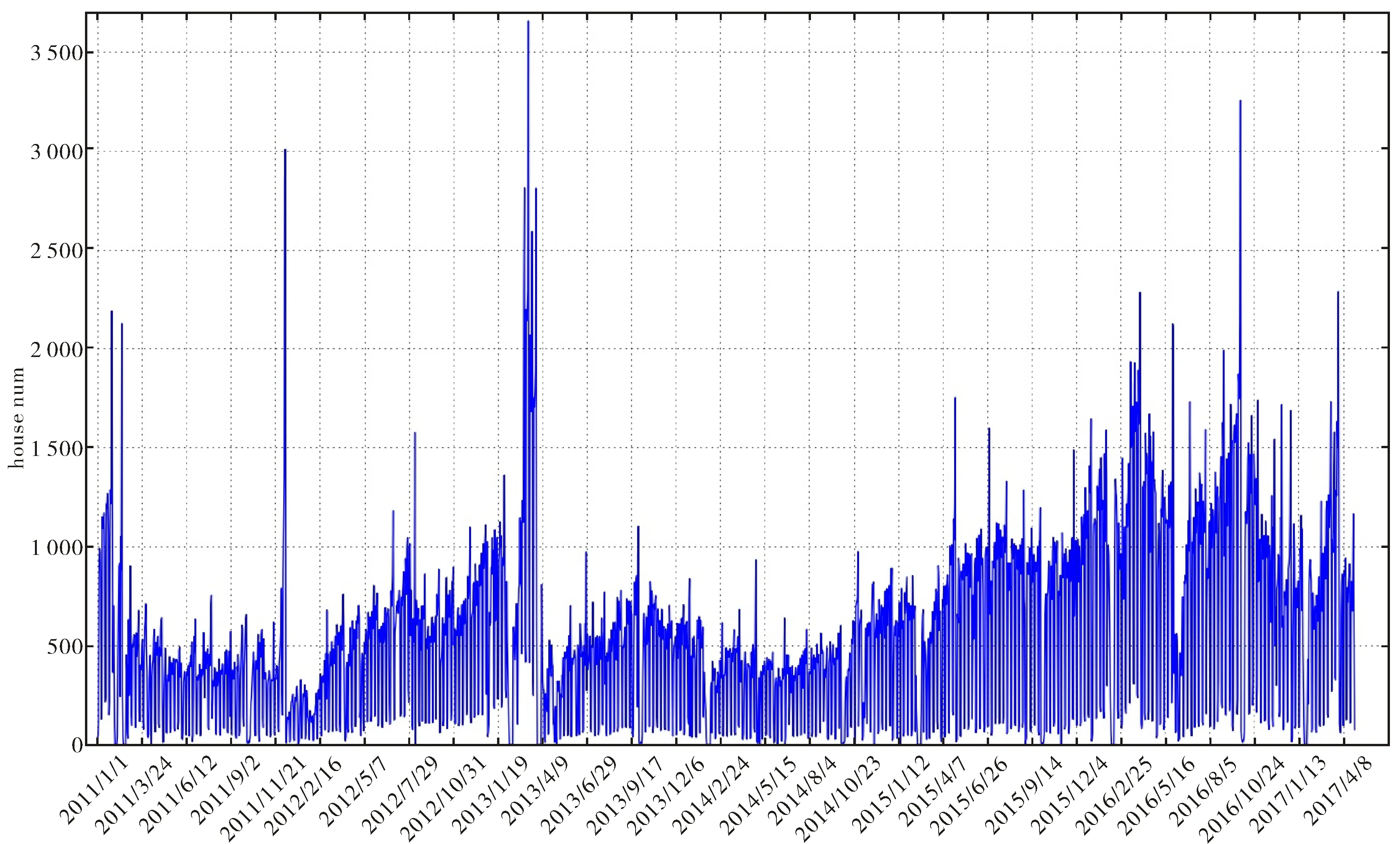
图10 北京市二手住宅市场交易统计Fig.10 The trade statistic in second-hand houses mark from Beijing

采用DFA去趋势检验法，利用相应年限的北京市二手住宅价格指数的月度数据(数据来源：Resset数据库)分别估计出第一时期和第二时期北京市房地产市场二手住宅价格指数的Hurst 指数，如图11所示.

计算出北京市两阶段的房地产住宅投资期望收益率与标准差，分别记为μ1，μ2，σ1，σ2.

对于无风险利率，它体现的名义货币增值的水平.本文选取两个阶段金融机构人民币活期存款基准利率(数据来源：中国人民银行货币政策司)对应年限的平均值作为各阶段的无风险利率参考值记为r1，r2.统计结果如表4所示.

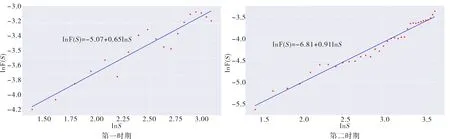
图11 北京市房地产市场Hurst指数估计Fig.11 Estimation of Hurst exponent in Beijing real estate market

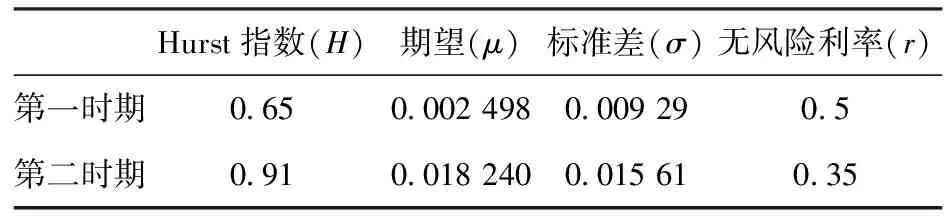
Hurst指数(H)期望(μ)标准差(σ)无风险利率(r)第一时期065000249800092905第二时期0910018240001561035

注：T为个人投资终止期限(投资者寿命)，在此处不加以考虑.

在第一时期里，中央政府连续出台房地产市场调控政策，打压房地产市场中的投机者：2011年多次上调人民币存款准备金率；新国八条出台，把二套房首付比例提至60%，贷款利率提至基准利率的1.1 倍，上调个人住房公积金贷款利率；2012年加快推进房产征收税；2013年新国5条出台，二手房交易的个人所得税由交易总额的1%调整到按差额的20%征收.此类举措的执行使得二手住宅价格指数的对数收益率平均值约为0.24%，这里，将标准差看作是波动率的近似值，发现二手住宅价格指数的对数收益率的波动率很小.说明在一定程度上遏制了房地产市场的交易，房价趋于平稳增长，但该时期市场的Hurst指数为0.65，呈现出分形特征.

2015年“9.30”房贷新政：全国40多个城市相继取消或者大幅度松绑限购；放宽公积金贷款；央行降息.继而转入第二时期，2015年5次降准降息，并降低公积金贷款利率，“330”政策明确降低商贷二套房首付比例；“831”政策降公积金最低首付至20%，新“930”政策将商贷首套房最低首付比例降至25%，公积金政策逐步放宽，持续降低购房门槛；2016年下调首套房首付比例，上调公积金存款利率，下调准备金率，营改增正式实施，并减免契税、营业税，制定购房补贴政策，鼓励农民工在城市购房.此时房地产市场Hurst 指数出现急剧增大的势头.说明二手住宅价格指数对数增长率前期的正增长会促使后期价格依然为正增长.

由本文所构造的房地产市场个人投资决策分析模型结论来看，较之第一时期，市场Hurst指数的增大会导致投资者做出停止决策的可行域扩大以及波动率的增大，会促使投资者在此种情况下卖出房产，即对二手住宅交易有推动作用.二手住宅的期望收益率增大，利率的降低，这两个因素会引起投资者执行停止决策的可行域缩小，对二手住宅的交易有抑制作用，由于Hurst指数与波动率的影响要大过期望收益率与利率，所以出现了二手住宅交易的繁盛时期.

5 总结

本文将房价的分形噪声考虑进来，研究房地产二手住宅市场，建模求解，从理论上分析了北京市近年来二手住宅交易市场在政府宏观调控下的发展情况.这说明政府可以通过中国二手住宅市场交易情况来“对症下药”，制定切实有效的房市调控政策来稳定房市.

[1] MASON S P， MERTON R C. Recent Advances in Corporate Finance[M].Homewood: R.D. Irwin， 1985:7-55.

[2] BLACK F， SCHOLES M. The pricing of options and corporate liabilities[J].Journal of Political Economy， 1973，81(3):637-659．

[3] ROSS S A. A simple approach to the valuation of risky streams[J]. Journal of Business， 1978，51(3):453-475．

[4] PETERS E. Fractal Market Analysis[M].New York:Wiley， 1994．

[5] NECULA C. Option Pricing in Fractional Brownian Motion Environment[R].Bucharest: Academy of Economic Studies, 2002．

[6] 黄文礼. 基于分数布朗运动模型的金融衍生品定价[D].杭州: 浙江大学， 2009．

[7] 孙玉东. 修正的Black-Scholes模型下的欧式期权定价[J].高校应用数学学报， 2012，27(1):23-32．

[8] TITMAN S. Urban land prices under uncertainty[J].American Economic Review， 1985，75(3):505-514．

[9] CLARKE H R， REED W J. A Stochastic analysis of land development timing and property valuation[J]. Regional Science and Urban Economics， 1988，18(3):357-381．

[10] GELTNER D， RDDIOUGH T， STOJANOVICH S. Insights on the effect of land use choice[J].Journal of Urban Economic， 1996，39(3):20-50．

[11] WILLIAMS J. Real estate development as an option[J].Journal of Real Estate Finance and Economics， 1991，4(2):191-208．

[12] CAPOZZA D， SICK G. The risk structure of land markets[J].Journal of Urban Economics， 1994，36(1):297-319．

[13] 蔡晓钰， 陈 忠， 蔡晓东. 个人房地产投资的相机策略及其可达性：一个最优停时分析框架[J].数量经济技术经济研究， 2005，22(3):88-96．

[14] 蔡晓钰， 韩丽川， 吴圣佳. 租赁还是购置—个人住房投资的时机选择问题[J].系统工程学报， 2006，21(3):280-286．

[15] 蔡晓钰， 陈 忠， 吴圣佳. 个人房地产最优租-售转换的ROs投资决策[J].管理科学学报， 2008，11(4):125-133．

[16] 韩 露. 实物期权理论在房地产投机时机决策中的应用[J].金融教学与研究， 2013，28(1):19-22．

[17] 谭 峻， 朱传梅. 用分形理论探讨中国大陆房地产市场波动性[J].中国房地产:学术版， 2014，3(2):11-18．

[18] 张卫国， 肖炜麟. 分数布朗运动下股本权证定价研究-模型与参数估计[M].北京：科学出版社， 2013: 107-112．

[19] 祈兆珍. 房租与房价的比价关系-《关于住房租金结构构成的研究》摘要之二[J].中国房地产， 2003，23(13):12-14．

Reviewmacro-controloftherealestatemarketbasedontheviewofpersonalinvestment

WU Di， GUO Sipei， HE Sui

(College of Mathematics and Statistics， Central China Normal University， Wuhan 430079, China)

According to empirical analysis to Chinese real estate market， this paper finds that the market has fractal feature and exists a kind of linear relation between house prices and rent. Under the premise of it， we use the real option theory to estimate investing earnings， then build the renting-selling conversion model and solve model by the stopping time and numerical simulation method， get the prices feasible sector of investors making renting-selling conversion decision. By analysing qualitatively the influence of Hurst exponent， growth rate of house prices， volatility， investment horizon and risk-free interest rate to feasible section of house prices, we draw a conclusion. In the end， this paper utilizes the conclusion to make periodic research to the market of second-hand residential real estate in Beijing and dissects a series of macro-control policy that the government made for the real estate market reversely ．

house prices; fractal feature; real option; stopping time; fractional Brownian motion

2017-07-12.

湖北省自然科学基金项目(2015CKB732)．

*E-mail: 550119360@qq.com.

10.19603/j.cnki.1000-1190.2017.06.003

1000-1190(2017)06-0736-11

F202

A