一种求解大规模方程组的修正Dai-Yuan共轭梯度法

黎 勇， 邓娌莉

(百色学院 数学与统计学院， 广西 百色 533000)

一种求解大规模方程组的修正Dai-Yuan共轭梯度法

黎 勇*， 邓娌莉

(百色学院 数学与统计学院， 广西 百色 533000)

设计一种针对大规模非线性方程组的修正DY共轭梯度算法.该算法的搜索方向不仅自动满足充分下降条件，而且属于信赖域.在适当条件下，可以证明新算法是全局收敛的.初步的数值实验表明新算法可以有效求解大规模非线性方程组．

非线性方程组； 共轭梯度法； 大规模； 信赖域； 全局收敛

考虑非线性方程组：

f(x)=0，x∈Rn，

(1)

其中f:Rn→Rn连续可微.求解此类问题的方法很多，将方程组问题转化为最优化问题是其中的一种思想.令

minφ(x)，x∈Rn，

(2)

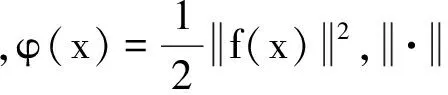
共轭梯度法的一般迭代格式如下：

xk+1=xk+αkdk，

(3)

(4)

其中,αk是步长，dk是搜索方向，不同的βk对应着不同的共轭梯度法，最经典的有HS方法、FR方法、PRP方法、DY方法等[1]．

不少研究人员在应用共轭梯度思想求解非线性方程组方面进行了讨论，也取得了较好的研究结果.本文受文献[2]和[3]的思想方法的启发，将在经典DY共轭梯度法的基础上，利用投影技术，提出一种修正的DY投影共轭梯度法．

1 算法

新算法的搜索方向设计如下：

dk+1=

(5)

其中,f(xk+1)=fk+1，f(xk)=fk，yk=fk+1-fk，而λ1>0，λ2>0是常数.在此基础上，下面将给出新算法.新算法采用以下线搜索[4]：

-f(xk+αkdk)Tdk≥

(6)

这里αk=max{s，λs，λ2s，…}，σ>0，s>0，λ∈(0，1)．

算法1(MDY算法)：

步0. 选取初始点x0∈Rn.常数ε∈(0，1)，参数λ1>0，λ2>0，σ>0.令k:=0．

步2. 利用(5)式计算搜索方向dk+1．

步3. 由线搜索技术(6)式计算步长αk．

步4. 利用以下公式计算下一个迭代点zk=xk+αkdk．

(7)

步6. 令k:=k+1.转步1．

注：(7)式表示算法的下一个迭代点xk+1应当通过将当前迭代点xk投射到超平面Hk={x∈Rnf(zk)T(x-zk)=0}上获得，这一思想由Solodov和Svaiter在文献[5]提出．

2 全局收敛性分析

引理1设dk满足(5)式，则有：

(8)

和

(9)

证明当k=0时，结论显然成立．

当k≥1时，根据(5)式可得

即(8)式成立．

依据(8)式，利用Cauchy-schwartz不等式得

故

综上所述，(9)式得证. 证毕.

上述引理说明新算法不仅自动具有独立于线搜索的充分下降性质，而且搜索方向具有信赖域性质，这两个重要性质对算法全局收敛性的证明非常重要.下面利用文献[2]和[3]的思想方法讨论新算法的全局收敛性.以下两个假设是后文讨论的依据：

假设(i)：非线性方程组(1)有解．

假设(ii)：f(x) Lipschitz 连续，即存在一个正的常数L，使得

(10)

由假设(ii)容易推出存在一个正的常数γ，使得

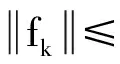
(11)

引理2若假设(i)、(ii)成立，则算法1是可行的．

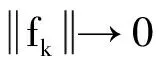
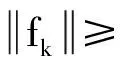
(12)

下面证明满足线搜索(6)式的步长有下界．

反证法.假设存在k′使(6)式不成立，则对∀m∈∪{0}，令有

由(8)式和假设(ii)有

(13)

而由(9)、(11)式可以推出

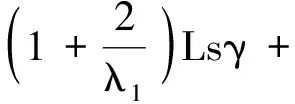
(14)

联立(9)、(13)、(14)式可得

引理3设序列{xk}由算法1产生，假设(i)、(ii)成立，且f(x*)=0，则

和

成立．

引理3及其证明详见文献[5]．

定理1若假设(i)、(ii)成立，αk，dk，xk，fk都由算法1产生，则

(15)

证明假设(15)式不成立，则存在一个正的常数η，使

由(9)式有

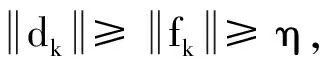
(16)

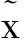
而由(9)、(11)式容易得到

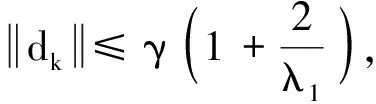
根据引理2、引理3以及(3)式容易知道

因此

(17)

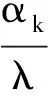
(18)

当k→∞时，对∀k∈N2，上式两边同取极限得

而(8)式两边同取极限得

矛盾.所以(15)式成立.证毕.

3 数值试验

本节将对MDY算法与传统DY算法在求解大规模非线性方程组方面进行数值试验和比较，测试的所有程序都是在Matlab R2010b上运行. 承担测试任务的计算机配置如下：Win 7.Pentium Dual E5800 3.20 GHz，内存2.0 G. 本次试验共选取文献[4]中的9个非线性函数进行测试，测试函数见表1．

表1 测试问题

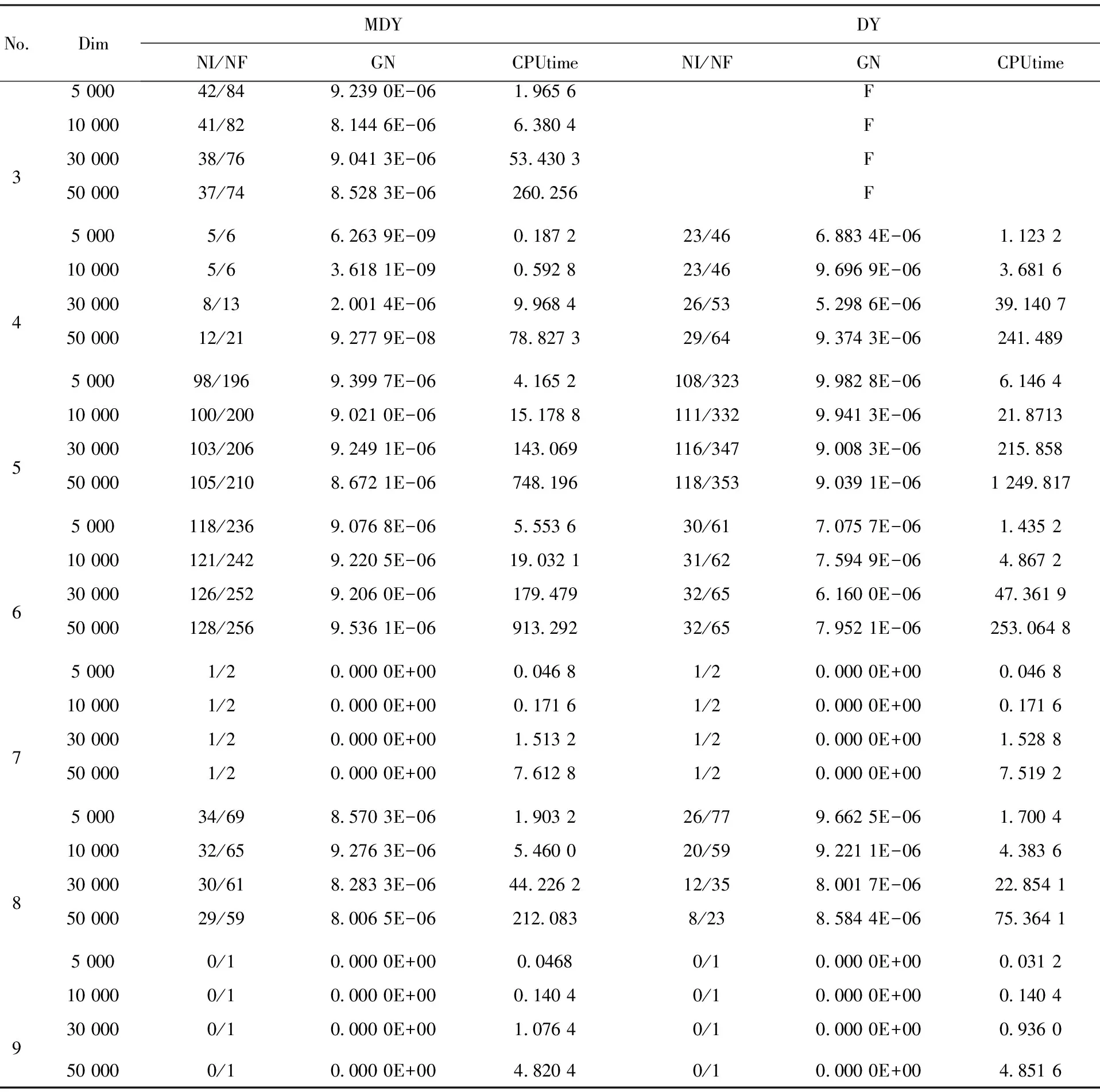
续表2

上表中No.表示测试问题的序号，Dim表示问题的维数，NI表示算法迭代次数，NF表示函数值的计算次数，GN表示程序终止时f(x)的范数值，CPUtime表示实验所需时间(单位为秒)，F表示失败.从表2中的数据容易看出，针对测试问题1，2，3，MDY算法能成功求解，而DY算法对这3个问题基本失败(问题2中的5 000维和30 000维情形除外).对问题4和5来说，MDY算法无论是迭代次数、函数值计算次数，或者是运算消耗时间上均优于DY算法.对问题7和9的求解效果，两种算法基本一致. 当然，在问题6和8的求解上，DY方法也一定程度上表现出了它的优势. 综上所述，我们认为新算法能够有效求解大规模非线性方程组问题，而且新算法MDY总体上的数值表现要优于传统的DY算法．

[1] 戴彧虹， 袁亚湘. 非线性共轭梯度法[M].上海:上海科技出版社，1999．

[2] YUAN G， ZHANG M. A three-terms Polak-Ribière-Polyak conjugate gradient algorithm for large-scale nonlinear equations[J]. Journal of Computational and Applied Mathematics， 2015，286: 186-195．

[3] YUAN G， ZHANG M， LI Y. A modified hestenes and stiefel conjugate gradient algorithm for large-scale nonsmooth minimizations and nonlinear equations[J]. Journal of Optimization Theory and Application， 2016，168: 129-152．

[4] LI Q， LI D. A class of derivative-free methods for large-scale nonlinear monotone equations[J]. IMA Journal of Numerical Analysis， 2011，31(4):1625-1635．

[5] SOLODOV M V， SVAITER B F. A Globally Convergent Inexact Newton Method for Systems of Monotone Equations[C]//FUKUSHIMA M， QI L. Reformulation: Nonsmooth， Piecewise Smooth， Semismooth and Smoothing Methods. US: Springer， 1998:355-369．

AmodifiedDai-Yuanconjugategradientalgorithmforlarge-scalenonlinearequations

LI Yong, DENG Lili

(School of Mathematics and Statistics， Baise University， Baise， Guangxi 533000, China)

This paper gives a modified Dai-Yuan conjugate gradient algorithm for large-scale nonlinear equations.The presented search direction not only possesses the sufficient descent property but also belongs to a trust region.The new algorithm has the global convergence under appropriate conditions.Numerical results show that this proposed algorithm is more effective than that of the normal method for large scale nonlinear equations．

nonlinear equation; conjugate gradient methods; large-scale; trust region; global convergence

2017-02-20.

国家自然科学基金项目(11661001，11661009)； 广西省自然科学基金项目(2014GXNSFAA118030)；广西省教育厅科研项目(YB2014389)．

*E-mail: liyong@3922@163.com．

10.19603/j.cnki.1000-1190.2017.06.002

1000-1190(2017)06-0731-05

O224

A