具阻尼项的二阶Emden-Fowler型泛函差分方程的振动准则
2017-12-26杨甲山
杨甲山
(1.梧州学院 信息与电子工程学院, 广西 梧州 543002; 2.梧州学院 复杂系统仿真与智能计算实验室, 广西 梧州 543002)
具阻尼项的二阶Emden-Fowler型泛函差分方程的振动准则
杨甲山1,2*
(1.梧州学院 信息与电子工程学院, 广西 梧州 543002; 2.梧州学院 复杂系统仿真与智能计算实验室, 广西 梧州 543002)
研究了二阶变时滞Emden-Fowler型阻尼差分方程Δ[Anφ(Δyn)]+Bnφ(Δyn)+Qnf(Φ(xσn))=0(n≥n0)的振动性,其中yn=xn+Png(xτn),φ(u)=|u|λ-1u,Φ(u)=|u|β-1u(这里λ>0,β>0为实常数). 利用广义的黎卡提变换,结合其它数学分析方法, 获得了该类方程的一系列新的振动准则,并给出了若干例子说明本文所得结果的有效性.
振动性; 中立型差分方程; 黎卡提变换; 阻尼项
随着差分系统的稳定性理论在计算机科学、自动控制理论、经济学、生物数学(特别是生物种群动力学)、物理学(特别是核物理)等自然科学和社会科学中的广泛应用,其有关理论的研究显得越来越重要,特别是差分方程的定性理论之一的振动性研究更是受到学者们高度关注[1-19].但值得注意的是,在这些研究中,对具有阻尼项的Emden-Fowler型差分方程研究却很少[7-9].本文考虑如下一类具有非线性中立项的二阶Emden-Fowler型阻尼泛函差分方程
Δ[Anφ(Δyn)]+Bnφ(Δyn)+Qnf(Φ(xσn))=0,
n≥n0,
(1)
的振动性,其中yn=xn+Png(xτn),n0≥0为整数;φ(u)=|u|λ-1u,Φ(u)=|u|β-1u(这里λ>0,β>0为实常数);而{An},{Pn},{Bn},{Qn},{τn},{σn}均为实数序列;函数f(u),g(u)∈C(R,R)且满足uf(u)>0(u≠0),ug(u)>0(u≠0).
关于方程(1)的解及其振动性定义,英文的可参见[1-2],中文的可参见[6,10].本文只讨论泛函差分方程(1)的非平凡解.记
(2)
并约定zn0=1. 假设:
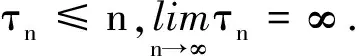
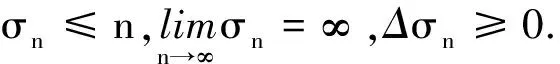
(H3) 当u≠0时,f(u)/u≥L,g(u)/u≤η,其中L>0, 0<η≤1均为常数.
(H4)0≤Pn<1,Qn>0,且An>Bn≥0.
文献[4]研究了方程(1)的特殊情形
Δ(pn|Δzn|λ-1Δzn)+qnf(xn-σ)=0
的振动性,这里zn=xn+pnxn-τ.但我们可以看到,若没有假设λ≥1,其结果是不成立的.
文献[5-6]分别研究了泛函差分方程
和
Δ(pn(Δ(xn+φ(n,xτn))γ))+qnfβ(xgn)=0
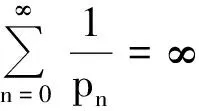
文献[10-11]研究了差分方程
Δ[rn|Δzn|α-1Δzn]+qnf(xn-σ)=0
本文利用Riccati变换和均法,并借助大量不等式,获得了方程(1)振动的一系列新的充分条件,扩充了α,β的范围,推广、改进且统一了文献[4-13,15]中的一些结果,还纠正了文[6]中定理4的证明中的错误.考虑这种情形:
(C)
并引入下列二重序列,后面不再说明.称二重序列{Hn,s:n≥s≥n0}属于集合Ω,记为Hn,s∈Ω,如果
(i) 当n≥n0时Hn,n=0; 当n>s≥n0时Hn,s>0;

引理1设(H1)~(H4)及条件(C)成立,并设序列{xn}是系统(1)的一个最终正解,则有
yn>0,Δyn>0,ΔAn|Δyn|λ-1Δyn<0.
(3)
证明因为序列{xn}是系统(1)的最终正解,故可设当n≥N≥n0时,xn>0,xτn>0,xσn>0,于是yn>0.由方程(1),并考虑到(H3),则有
Δ[Anφ(Δyn)]+Bnφ(Δyn)≤-LQn(xσn)β<0.
(4)
利用(2)式,得
Δzn=zn+1-zn=
注意到上式及(4)式,于是就有
Δ[znAnφ(Δyn)]=
zn+1·Δ[Anφ(Δyn)]+Δzn·[An|φ(Δyn)]=

zn+1Δ[Anφ(Δyn)]+Bnφ(Δyn)<0,
(5)
这就是说znAnφ(Δyn)=zn(An|Δyn|λ-1Δyn)是单调减少的,且Δyn最终定号.由此可断言:Δyn>0,n≥N.
若不然,则∃n1≥N,使得Δyn1<0,因此
zn(An|Δyn|λ-1Δyn)≤
zn1(An1|Δyn1|λ-1Δyn1)=-M,n≥n1,
上式中的常数M=-zn1(An1|Δyn1|λ-1Δyn1)=zn1[An1|Δyn1|λ-1(-Δyn1)]>0.于是
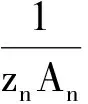
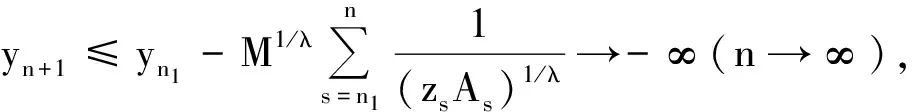
由(4)式不难推出ΔAn|Δyn|λ-1Δyn<0,n≥N.证毕.
引理2[17]设X,Y为非负实数,则当r>1时rXYr-1-Xr≤(r-1)Yr,等号成立当且仅当X=Y.
1 方程(1)的振动准则
定理1设(H1)~(H4)及条件(C)成立,且存在一正的序列{ρn}使得当λ≥β≥1时
(6)
其中M>0为某常数,则方程(1)是振动的.
证明反设方程(1)存在一个非振动解{xn},即xn>0,xτn>0,xσn>0,n≥N≥n0. 由于yn≥xn, 注意到条件(H1)及(3)式, 由序列{yn}的定义, 有
yn≤xn+ηPnxτn≤xn+ηPnyτn≤xn+ηPnyn,
即
xn≥[1-ηPn]yn.
(7)
定义变换
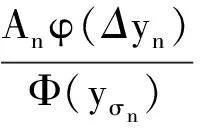
(8)
则wn>0(n≥N). 由引理1知Aσn(Δyσn)λ≥An(Δyn)λ≥An+1(Δyn+1)λ,所以
(9)
由于β≥1,利用不等式(见[13]的引理2)xβ-yβ≥21-β(x-y)β,x≥y≥0,得
Δ(yσn)β=(yσn+1)β-(yσn)β≥
21-β(yσn+1-yσn)β=21-β(Δyσn)β>0.
(10)
于是分别利用(4), (10)和(7)式, 并注意到yσn≤yσn+1, 由(8)式进一步可得
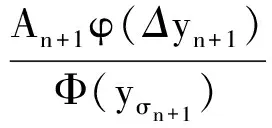

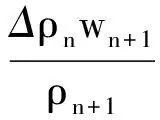
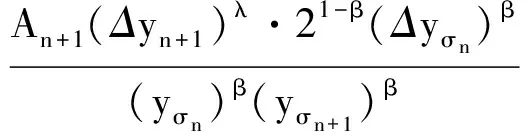
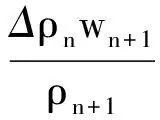
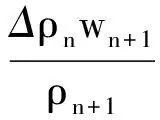
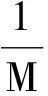
Δwn≤-LρnQn(1-ηPσn)β+
(11)
由(11)式,并利用完全平方技巧,得
Δwn≤-LρnQn(1-ηPσn)β-
-LρnQn(1-ηPσn)β+
两边从n1到n求和,得
wn1-wn+1≤wn1,
这与(6)式矛盾! 证毕.
定理2设(H1)~(H4)及条件(C)成立,且ΔAn≥0,如果存在一正的序列{ρn}使得当λ≥β时
(12)
其中α>0为某常数,则方程(1)是振动的.
证明反设方程(1)存在一个非振动解{xn},即xn>0,xτn>0,xσn>0,n≥N≥n0.定义序列wn同(8)式,则当n≥N时,wn>0.
当β≥1时,利用不等式(见[14]的定理41)xβ-yβ≥βyβ-1(x-y),x≥y≥0,得
Δ(yσn)β=(yσn+1)β-(yσn)β≥
β(yσn)β-1(yσn+1-yσn)=β(yσn)β-1Δyσn.
(13)
于是, 分别利用(4), (13),(9)和(7)式,并注意到yσn≤yσn+1,由(8)式得
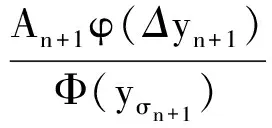
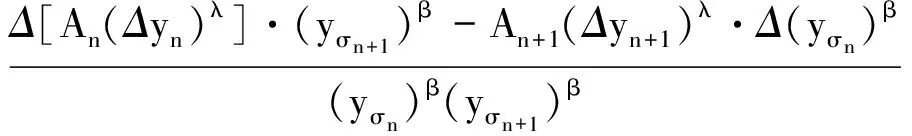
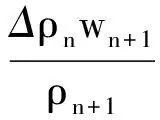

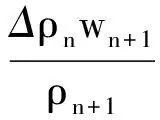
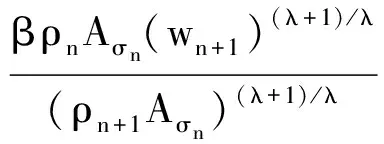
(14)
当0<β<1时,利用不等式(见[14]的定理41)xβ-yβ≥βxβ-1(x-y),x≥y>0,得
Δ(yσn)β=(yσn+1)β-(yσn)β≥
β(yσn+1)β-1(yσn+1-yσn)=β(yσn+1)β-1Δyσn>0.
(15)
同样,由于(9)式及yσn≤yσn+1,并分别利用(4),(15)和(7)式,由(8)式得
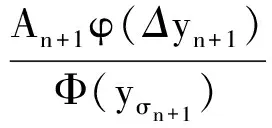
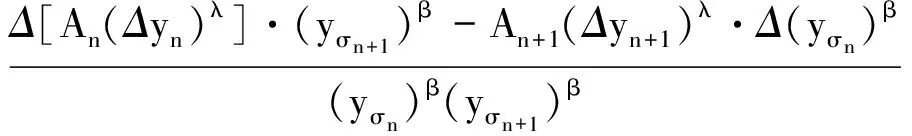
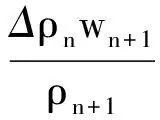
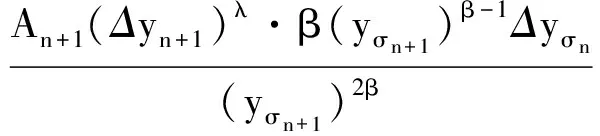
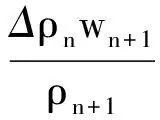
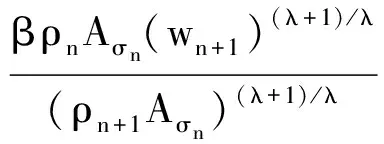
即(14)式仍然成立.由引理1知,当n≥N时,
0>ΔAn|Δyn|λ-1Δyn=ΔAn(Δyn)λ=
ΔAn·(Δyn+1)λ+AnΔ(Δyn)λ,
注意到ΔAn≥0,所以Δ(Δyn)λ<0,即{(Δyn)λ}是非增的序列.因此,∀n≥N,有(Δyn)λ≤(ΔyN)λ,即Δyn≤ΔyN.于是,yn≤yN+(n-N)ΔyN≤yN+nΔyN.故存在合适的正常数α,使得yn≤αn.由此可得,当n≥N时yσn+1≤ασn+1≤α(n+1),进而
(yσn+1)(λ-β)/λ≤[α(n+1)](λ-β)/λ,n≥N.
因此(14)式即为
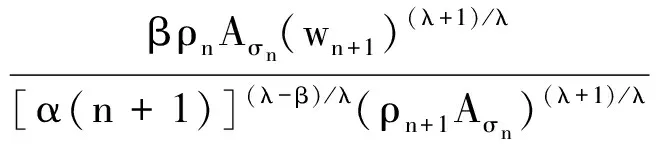
(16)
在引理2中,令
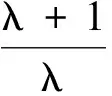
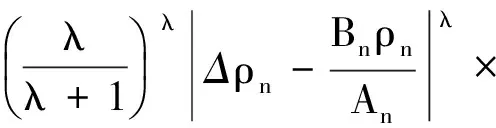
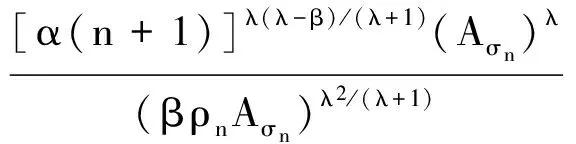
则由不等式rXYr-1-Xr≤(r-1)Yr可得
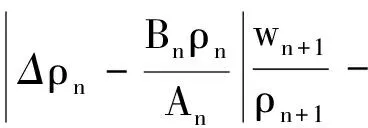
将上式代入(16)式,得
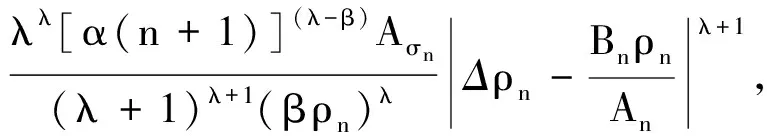
上式整理后,两边从N到n求和, 得
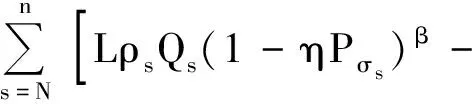
这与(12)式矛盾! 证毕.
定理3设(H1)~(H4)及条件(C)成立,β≥λ≥1,且存在正的序列{ρn}及二重序列Hn,s∈Ω,使得
(17)
在上面的式子中M>0为某常数,则方程(1)是振动的.
证明反设方程(1)存在一个非振动解{xn},即xn>0,xτn>0,xσn>0,n≥N≥n0.定义序列wn同(8)式.类似地,由定理1的证明知(11)式成立,即
上式两边同乘以Hn,s, 然后从n1(n1≥N)到n-1(n>n1)求和,得
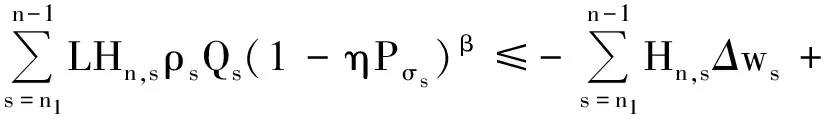
对上式右边第一项分部求和,然后利用完全平方技巧,得

因此
由上式进一步可得
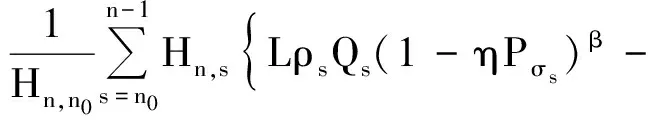
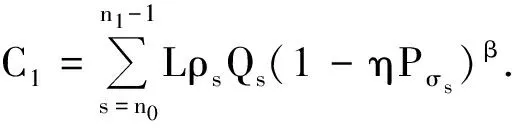
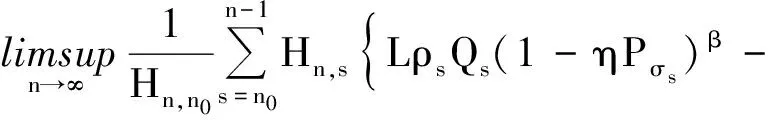
这与(17)式矛盾! 证毕.
注1当λ=β时,由定理1和定理3分别可得文[8]中的定理1和定理2.
定理4设(H1)~(H4)及条件(C)成立,且ΔAn≥0,λ≥β,如果存在正的序列{ρn}及二重序列Hn,s∈Ω,使得
∞,
(18)
式中,α>0为某常数,则方程(1)是振动的.
证明反设方程(1)存在一个非振动解{xn},即xn>0,xτn>0,xσn>0,n≥N≥n0.定义序列wn同(8)式.类似地,由定理2的证明知(16)式总是成立,即
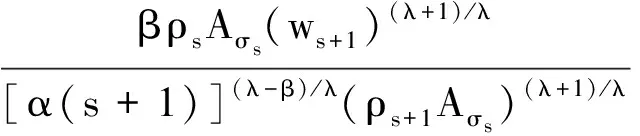
于是由上式可得
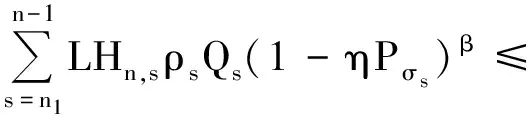
在引理2中,令
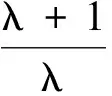
则由不等式rXYr-1-Xr≤(r-1)Yr可得

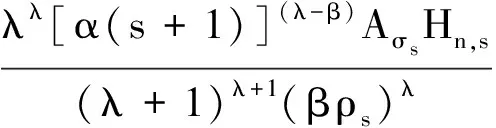
于是
即
wn1,
由上式即得
于是就有
∞,
这就与(18)式产生了矛盾! 定理证毕.
注2在[6]中,作者通过下面的不等式(见[6]的P322第16行)
(Δ2zn)γ=(Δzn+1-Δzn)γ≤
(Δzn+1)γ-(Δzn)γ<0,
此处,γ>1是两正奇数之比,即Δ2zn<0得到了与定理4类似的定理([6]中的定理4).但上述不等式是错的,它成立的条件是Δzn+1≥Δzn(见[6]中的(2.8)式),这就与Δ2zn<0产生了矛盾.所以,我们的定理4不仅纠正了这个错误,而且定理2及定理4还进一步拓广了γ的范围.
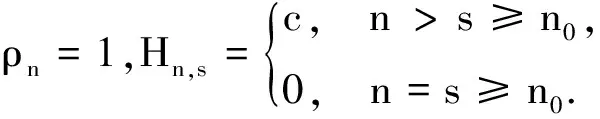
推论1设(H1)~(H4)及条件(C)成立,且β≥λ≥1,如果
(19)
其中,M>0为某常数,则方程(1)是振动的.
推论2设(H1)~(H4)及条件(C)成立,且ΔAn≥0,λ≥β,如果
(20)
其中,α>0为某常数,则方程(1)是振动的.
再令Hn,s=(n-s)ω,ω≥1,n≥s≥n0,类似地,可得
推论3设(H1)~(H4)及条件(C)成立,且β≥λ≥1,如果存在正的序列{ρn},使得
(21)
其中,M>0为某常数,则方程(1)是振动的.
推论4设(H1)~(H4)及条件(C)成立,且ΔAn≥0,λ≥β,如果存在正的序列{ρn},使得
(22)
其中,α>0为某常数,则方程(1)是振动的.
注4当β=λ时,由定理3还可得到文[9]中的定理1.进一步,若方程(1)中的β=λ≥1是2个正奇数之商,且g(u)=u,τn=n-τ,Bn≡0,f(u)=u,σn=n-σ,则方程(1)简化为
在这种情形下,推论3就是文[15]中的定理3.1. 因此,本文定理改进且推广了文[15]中的几个定理.
2 例子
例1考虑下列Emden-Fowler型时滞差分方程:

(23)
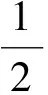
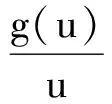
所以条件(H1)~(H4)及(C)显然是满足的.又因为ΔAn≥0,且
所以,由推论2知方程(23)是振动的.
例2考虑具非线性中立项的二阶Emden-Fowler型阻尼泛函差分方程:

(24)

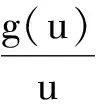

5=L(u≠0),
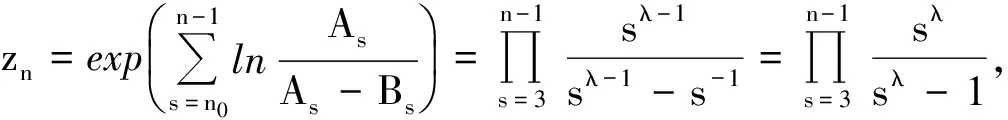
∞,
显然,条件(H1)~(H4)及(C)全部满足.为了计算简单,现在定理1中取ρn≡1,则
(n→∞),
所以,由定理1知方程(24)是振动的.
注5显然,文献[4-13,15-19]等中的定理都不适用于方程(23)和(24),因此本文所得到的结果是新的.
[1] AGARWAL R P. Difference Equations and Inequalities, Theory, Methods and Applications[M]. 2nd Ed. New York:Marcel Dekker, 2000.
[2] AGARWAL R P, BOHNER M, GRACE S R, et al. Discrete Oscillation Theory[M]. New York :Hindawi Publishing Ororation,2005.
[3] SAKER S H, CHENG S S. Kamenev type oscillation criteria for nonlinear difference equations[J]. Czechoslovak Mathematical Journal, 2004,54: 955-967.
[4] LUO J W. Oscillation criteria for second-order quasilinear neutral difference equations[J]. Comput Math Appl, 2002,43:1549-1557.
[5] CHENG G F. Kamenev-type oscillation criteria for delay difference equations[J]. Acta Mathematica Scientia, 2007,27(3): 574-580.
[6] 程金发. 二阶泛函差分方程的振动性判别准则[J].数学学报,2006,49(2):317-326.
[7] 田亚州, 范 敏, 孟凡伟. 二阶非线性时滞差分方程解的振动性[J].数学的实践与认识, 2011,41(24):188-193.
[8] 杨甲山, 黄 劲. 一类具阻尼项的二阶差分方程的振荡性[J].昆明理工大学学报(自然科学版),2015,40(4): 131-138.
[9] 杨甲山, 张晓建. 具阻尼项的二阶拟线性泛函差分方程的振荡性判别准则[J].浙江大学学报(理学版), 2015,42(3): 276-281.
[10] 王冬梅, 徐志庭. 二阶拟线性中立型差分方程的振动性[J].应用数学学报, 2011,34(3):537-553.
[11] WANG D M, XU Z T. Oscillation of second-order quasilinear neutral delay difference equations[J].Acta Mathematicae Applicatae Sinica(English Series), 2011,27(1):93-104.
[12] 杨甲山. 具正负系数和多变时滞的高阶泛函差分方程的振动性定理[J].昆明理工大学学报(自然科学版), 2014,39(6):130-135.
[13] JIANG J C. Oscillation criteria for second-order quasilinear neutral delay difference equations[J]. Appl Math Comput,2002,125:287-293.
[14] HARDY G H, LITTLEWOOD J E, POLYA G. Inequalities[M]. 2nd Ed. Cambridge :Cambridge University Press, 1952.
[15] ZHANG B G,SAKER S H. Kamenev-type oscillation criteria for nonlinear neutral delay difference equations[J].Indian J Pure Appl Math, 2003,34(11):1571-1584.
[16] ZHANG B S. Oscillatory behavior of solutions of general third order mixed neutral difference equations[J].Acta Mathematicae Applicatae Sinica(English Series),2015,31(2):467-474.
[17] AGARWAL R P, BOHNER M, LI W T. Nonoscillation and Oscillation: Theory for Functional Differential Equations[M]. New York: Marcel Dekker, 2004.
[18] 杨甲山. 具正负系数的二阶非线性变时滞差分方程的振动性定理[J].中央民族大学学报(自然科学版), 2016,25(3): 26-31.
[19] 杨甲山. 一类具正负系数的二阶阻尼差分方程的振动定理[J].邵阳学院学报(自然科学版), 2012,9(2):6-10.
Oscillationcriteriaforsecond-orderEmden-Fowlerfunctionaldifferenceequationswithdamping
YANG Jiashan1,2
(1.School of Information and Electronic Engineering, Wuzhou University, Wuzhou 543002, China; 2.Laboratory of Complex System Simulation and Intelligent Computing, Wuzhou University,Wuzhou 543002, China)
This paper is concerned with oscillations of second-order variable delay Emden-Fowler damped difference equations of the form Δ[Anφ(Δyn)]+Bnφ(Δyn)+Qnf(Φ(xσn))=0(n≥n0),whereyn=xn+Png(xτn),φ(u)=|u|λ-1u,Φ(u)=|u|β-1u(λ>0,β>0 are constants).By using the generalized Riccati transformation, averaging technique and mathematical analytic methods, some new oscillation criteria for the equations are proposed. Finally, some illustrating examples have also been provided to show the importance of these results.
oscillation; neutral difference equation; Riccati transformation; damping term
2016-11-08.
国家青年科学基金项目(61503171);广西省教育厅科研项目(2013YB223) ;硕士学位授予单位立项建设项目(桂学位[2013]4号);梧州学院校级科研重大项目(2014A003).
*E-mail: syxyyjs@qq.com.
10.19603/j.cnki.1000-1190.2017.06.001
1000-1190(2017)06-0723-08
O175.7
A
