剪切、挤压变形应力分析探索

张超平，代红涛

(郑州铁路职业技术学院，河南 郑州 451460)

剪切、挤压变形应力分析探索

张超平，代红涛

(郑州铁路职业技术学院，河南 郑州 451460)

在目前材料力学课程的教材和教学中，对剪切与挤压变形的应力分析一般只做简单的陈述，便引出了剪切与挤压变形的剪切面和挤压面上的切应力和挤压应力的近似计算公式，即实用计算法。按照构件变形应力的一般研究方法从几何关系、物理关系、静力学关系三个方面对剪切、挤压变形进行应力分析，得出剪切、挤压应力的计算公式，对于一般教材和教学中采用的剪切、挤压应力的实用计算法的讲解是一个理论上的补充，有利于学生掌握和理解该内容。

切应力；挤压应力；变形；几何关系；物理关系；静力学关系

材料力学主要研究构件在不同变形下的承载能力，而在绝大部分教材中，都把构件的变形分为拉(压)变形、剪切(挤压)变形、扭转变形、弯曲变形、组合变形等进行研究。其中拉(压)、扭转、弯曲等变形应力的研究方法非常相似，都是通过试验观察，经过几何关系、物理关系、静力学关系三方面的分析得出最终结论，而把剪切(挤压)变形说得非常复杂，以致不能采用和其他变形一样的研究方法来分析应力，人为地假设出与众不同的实用计算方法，使教师讲解起来感觉说服力不强，底气不足，学生学起来既没有理论或实际上的受力分析，也没有正确的数学公式推导。因此，教师和学生普遍感到这部分内容理论性太强、逻辑性太差。经过分析发现，剪切和挤压变形中切应力和挤压应力的计算公式完全可以和其他变形一样，通过试验观察，经过几何关系、物理关系、静力学关系三方面的分析，得出同样的应力计算公式。

1 剪切变形切应力计算公式的推导

1.1 几何关系方面

(a) (b) (c) (d)

现在我们来研究图1(a)所示的铆钉受剪情况。由于两个外力F不在同一直线上，形成一对力偶，尚需有两个力FN形成另一对力偶来与其平衡，如图1(d)所示。铆钉除剪切变形外，还有弯曲变形、拉伸变形等，铆钉与被连接件因互相接触传力而产生挤压变形，因而，铆钉的实际受力情况非常复杂。但是剪切变形与破坏是发生在相对错动的平面之间的微段上，因此，我们可以认为在这一微段上主要因剪切力造成构件的变形和破坏，其他力所产生的变形可以忽略不计。如图2所示，取出这一微段进行试验，观察其变形。在变形前沿构件轴线划出两条纵向线和垂直于轴线的两条圆周线，在载荷F作用下(剪切力FQ=F)，注意观察变形，我们可以看到：原来为直线的纵向线(ab、cd)变形后仍为直线，只是相对于原来轴线倾斜了一个角度γ；原来是圆的圆周线(ac、bd)变形后仍为圆，且仍处在同一平面内，只是相对错动了一个位置。因此，可以得出如下平面假设：变形前为平面的横截面，在变形后仍为平面，仅相对错动了一个位置，横截面的形状、大小和间距均不发生变化。由此可以得出，横截面上各点均移动了相同的距离。根据剪(角)应变的定义可知，各矩形的直角改变量称为角应变γ，从而得出在剪切变形中横截面上各点的切应变相等，即γ=常数。

(a) (b)

1.2 物理关系方面

由剪切胡克定律，当切应力小于材料的比例极限时，切应力与切应变成正比，即τ=Gγ。因为材料是均匀的，所以G=常数，从而得到τ=Gγ=常数，即剪切变形中横截面上各点的切应力相等。

1.3 静力学关系方面

由静力平衡条件可知，横截面上切应力的合力等于剪切变形的内力——剪力FQ。设横截面(剪切面)面积为A，它上的切应力为τ，则

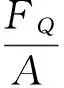
2 挤压变形应力的计算公式推导

我们来分析图3所示键的受力情况。挤压变形发生在键与轮或轴与键的接触面附近。

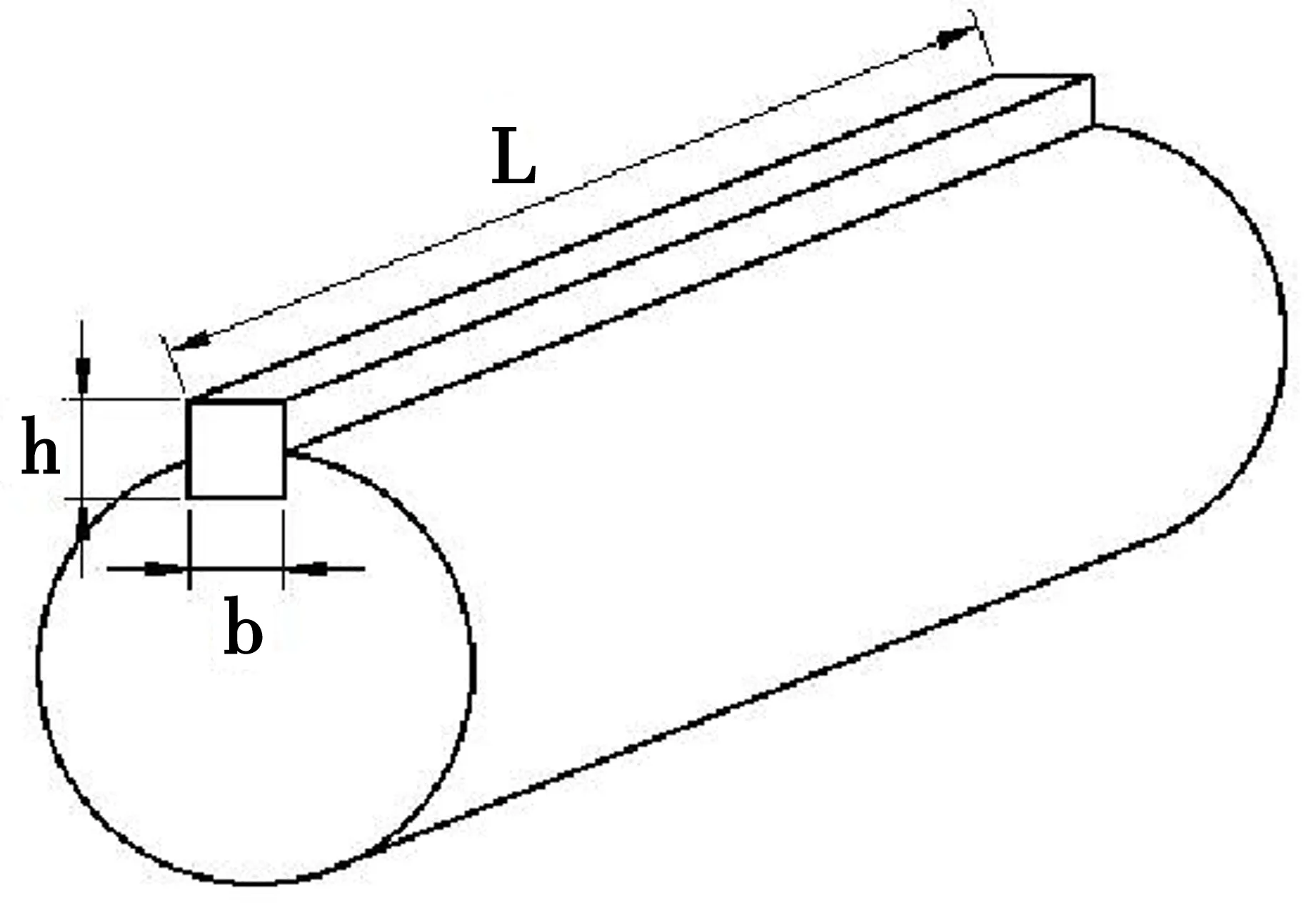
图3 受力情况图

(a) (b)

2.1 几何关系方面

如果把键的宽度b作为纵向，高度h和长度L 作为横向，加载前在接触部位附近处划出一系列纵向线和横向线，如图4(a)，加载后可以看出：各横向线和纵向线仍为直线，横向线发生了平移，如图4(b)。由此得到平面假设：接触面附近处的横截面(挤压面)变形前是平面，变形后仍是平面，只是相对于原位置发生了平移。由平面假设可得：横截面(挤压面)上各点的纵向变形相等，即正应变相等，ε=常数。

2.2 物理关系方面

由拉压胡克定律σ=Eε可得σc=常数，即横截面(挤压面)上各点的正应力相等。

2.3 静力学关系方面

设挤压面面积为Ac，挤压力为Fc，挤压应力 为σc，则

对于铆钉、销钉、螺栓等连接件，其挤压接触面是半圆柱面，实际挤压应力的分布是不均匀的，因此，不能按照以上公式计算挤压应力。

(a) (b)

图5半圆柱面挤压力图

如图5所示，铆钉连接，半圆柱挤压面上的挤压力为Fc，圆柱直径为D，挤压面长度为t，假设挤压面上挤压应力大小均匀，即σc=常数，根据静力学平衡条件得

由上式求得的应力与实际挤压应力(不均匀)的最大值相等，故可以用此式进行挤压面是圆柱面的挤压强度计算。

3 结语

以上是按照材料力学研究构件变形应力的一般方法，即从几何关系、物理关系、静力学关系三个方面通过对剪切、挤压变形的应力分析，得出发生剪切变形的构件剪切、挤压应力的计算公式。这样，对一般教材和讲授中采用的剪切、挤压应力的实用计算法是一个理论上的补充，有利于学生对这部分内容的理解和掌握。

[1]张晖辉，陈鐾，刘峰.对材料力学中挤压实用计算公式的讨论[J].力学与实践，2012(4)：83-86.

[2]袁权，任柯.关于材料力学中应力分析适用性的探讨—以挤压应力的实用计算为例[J].四川建材，2016，42(4)：287-288.

[3]古滨，邱清水，唐学彬.材料力学[M].武汉：武汉大学出版社，2014.

[4]张勤，张超平.工程力学[M].北京：高等教育出版社，2015.

AStudyonStressAnalysisofShearandExtrusionDeformation

ZHANG Chaoping, DAI Hongtao

(Zhengzhou Railway Vocational and Technical College, Zhengzhou 451460,China)

At present in the course of materials mechanics and teaching materials, Stress analysis of shear and extrusion deformation is generally only a simple analysis of statements, The approximate calculation formulas of shear stress and extrusion stress on the shear and extrusion deformation shear plane and the extrusion surface are derived, namely the practical calculation method. In this paper, stress analysis of shear and extrusion deformation is carried out from geometrical, physical and static relations according to the general research method of deformation stress, and the formulas for calculating the shear and extrusion stresses are obtained. The general teaching materials and teaching used in the shear, extrusion stress practical calculation method is a theoretical supplement to help students master and understand the content.

shear stress；extrusion stress；deformation；geometric relationship；physical relationship； statics relation

2016 - 12- 01

张超平(1962—)，男，河南开封人，郑州铁路职业技术学院建筑工程系副教授，研究方向为工程力学和工程材料。代红涛(1986—)，男，河南郑州人，郑州铁路职业技术学院建筑工程系助教，硕士，研究方向为建筑结构设计。

0341

A

1008-6811(2017)03-0017-03

赵 伟]