FGM圆筒形薄壳热屈曲临界温度理论解及修正

李耀宙， 王泽武

(1. 太原工业学院 环境与安全工程系， 山西 太原 030008；2. 大连理工大学 化工机械与安全学院， 辽宁 大连 116024)

FGM圆筒形薄壳热屈曲临界温度理论解及修正

李耀宙1， 王泽武2

(1. 太原工业学院 环境与安全工程系， 山西 太原 030008；2. 大连理工大学 化工机械与安全学院， 辽宁 大连 116024)

针对现有功能梯度材料(FGM)圆筒形薄壳热屈曲临界温度不一致的问题， 基于Donnell方程导出功能梯度材料圆筒形薄壳热屈曲临界温升理论解， 然后通过有限元方法得到功能梯度材料圆筒形薄壳热屈曲数值解， 通过对圆筒形薄壳的不同长径比l/R， 厚径比δ/R和半径R的理论解与数值解进行对比分析， 进而提出功能梯度材料圆筒形薄壳热屈曲临界温度修正解. 研究成果将有利于对类似功能梯度材料薄壳结构热稳定性问题进行精细化设计.

功能梯度材料； 圆柱壳； 热屈曲； 临界温度

0 引 言

功能梯度材料是由韧性较好的金属和耐高温的陶瓷两相材料组成， 这类材料的板壳结构在航天航空、核电和石油化工领域拥有广泛的应用前景. 近年来FGM板壳结构的热响应问题已被深入研究， 同时热稳定性问题也取得一定进展， 如在薄板方面， S. Shariat等人[1]基于高阶稳定性方程研究了功能梯度矩形板热屈曲问题. A. M. Zenkour[2]基于正弦剪切平板理论推导了功能梯度材料矩形薄板热屈曲方程. Wu等人[3]基于一阶剪切变形理论研究了FGM中厚度板的热屈曲问题. 朱甚等人[4]基于板的小挠度理论及ANSYS软件对矩形薄板的脱层热屈曲进行数值模拟分析. 在圆筒形壳方面， H.Yaghoobi等人[5]研究了材料特性沿轴向梯度变化圆筒形薄壳热屈曲问题. R.Shahsiah等人[6]基于一阶剪切变形理论研究了FGM圆筒形薄壳热屈曲. Wu等人[7]基于Donnell壳理论研究了FGM圆筒形壳的热弹性稳定性问题. 黄怀纬等人[8]采用能量法推导了功能梯度材料圆柱壳在不同温度梯度下的热屈曲公式. 但通过比较文献[6]和文献[7]可以发现， 同一FGM圆筒形薄壳结构热屈曲问题得出的临界温度理论解有差异， 这给FGM圆筒形薄壳热屈曲临界温度计算和结构设计带来困难. 为此本文借助有限元软件ANSYS求解得到FGM矩形平板在均匀温升下的数值解， 与理论解对比分析， 验证数值模型的准确性. 借助Donnell理论详细推导FGM圆筒形薄壳在均匀温升下的理论解， 与ANSYS得到的模型数值解对比分析， 提出理论解修正系数， 最后修正结果与数值解一致， 为FGM圆筒形薄壳避免热屈曲现象提供理论参考依据.

1 理论分析

本文采用FGM圆筒形薄壳坐标系如图 1 所示.

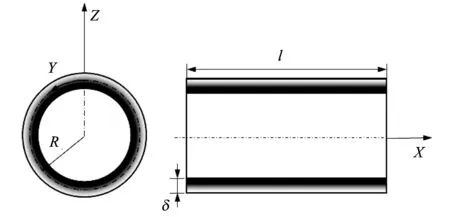
图 1 FGM圆筒形薄壳坐标系统Fig.1 Coordinate system of the FGM thin-wall cylindrical shell

1.1 基本方程

壳体沿X(轴向)，Y(环向)方向的正应变εx，εy和剪应变γxy分别表示为

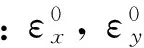
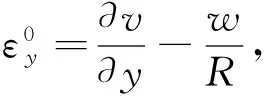
式中：u,v和w分别表示X，Y和Z方向的位移；R表示FGM圆筒形薄壳的半径.

1.2 FGM圆筒形薄壳热屈曲理论解

FGM圆筒形薄壳被置于温升ΔT的环境下， 则热效应的本构关系表示为

σx=E(z)[εx+μεy-ΔT(1+μ)α]/(1-μ2),

σy=E(z)[εy+μεx-ΔT(1+μ)α]/(1-μ2),

式中：μ为泊松比；σx和σy分别为沿X和Y轴方向上的正应力；τxy为剪应力；E(z)表示FGM弹性模量函数且E(z)=Ec+(Em-Ec)(1/2+z/δ)k=Ec+Emc(1/2+z/δ)k，Ec和Em分别表示陶瓷材质和金属材质的弹性模量，k表示FGM的成分梯度因子.

对FGM圆筒形薄壳， 单位长度上的内力Nx，Ny，Nxy和内力矩Mx，My，Mxy可以表示为

将式(3)代入式(4)， 得

其中

Ω1=Ecδ+Emcδ/(k+1),

Ω2=kEmcδ2/[2(k+1)(k+2)],

Ω3=Ecδ3/12+Emcδ3{1/(k+3)-

同时，φ和ϑ是温升函数ΔT引起的内力和内力矩的附加值.

结合式(5)和式(6)得， 由于温升函数ΔT引起的内力和内力矩的附加值可以用式(7)表示， 即

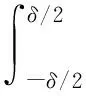
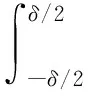
将式(2)代入式(5)得

根据Donnell薄壳简化准则[9]， 功能梯度材料的圆筒形薄壳平衡方程可以表示为

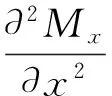
将式(8)代入式(9)得

Π11+Π12+Π13=0,

Π21+Π22+Π23=0,

其中

将式(10)中的第一式对x求导， 将式(10)中的第二式对y求导， 再相加代入第三式， 得

现利用临界平衡方法建立板的稳定性方程， 假设w0和T0为稳定状态的挠度和温度初始值， 在式(11)中分别给w和T一个微小的改变， 即w→w0+δw，T→T0+δT， 其中， 它们满足屈曲前后的平衡状态. 将w和T代入式(11)减去原来的平衡方程， 略去高阶项后得到屈曲方程， 记δw和δφ为w1和T1， 并且对式(11)再次进行四阶微元化， 则有

假设FGM圆筒形薄壳在均匀温升下， 径向和环向自由膨胀， 并且初始温度各处相同， 各处温度变化ΔT也相同， 得

将式(13)代入式(12)， 得

若FGM圆筒形薄壳边界条件为简支， 则位移函数可写成

式中：c为任意常数；m为圆筒形薄壳屈曲时沿X方向的半波数；n为环向全波数.

将式(15)代入式(14)， 得

借助Timoshenko外压屈曲理论推导方法， 为了得到临界温升， 将φ取最小值.

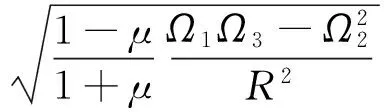
即得

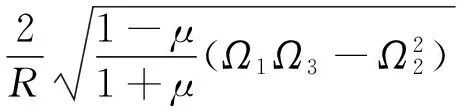
当在均匀温升条件下， 由式(7)得

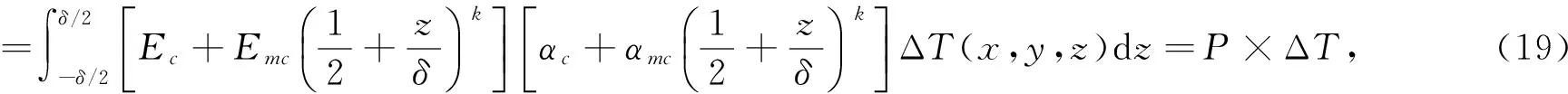
其中

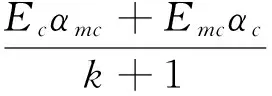
由式(18)和式(19)， 临界温升可以表示为

1.3 FGM矩形平板热屈曲理论解

当FGM矩形平板只承受均匀热载荷作用时， 得平板的平衡方程为

由于均匀温升引起的FGM矩形平板内力可表示为

将式(23)代入式(22)， 得

当FGM矩形平板的边界为简支约束时， 得边界条件为

式中：a，b为平板长和宽；m,n为板屈曲时沿X，Y方向的半波数；c为任意常数.

将式(7)和式(25)代入式(24)， 整理得

对于FGM平板的热屈曲问题， 当m=n=1时， 此时的临界温升可以表示为

2 数值分析与结果讨论

2.1 FGM矩形平板热屈曲数值分析

为了检验FGM圆筒形薄壳有限元数值解的准确性， 先建立一个FGM矩形平板数值模型. 选用ANSYS软件Shell281高阶单元， 进行网格划分， 并在平板四边施加简支边界条件， 即约束平板的X，Y和Z方向位移以及MX，MY，MZ方向弯矩， 同时施加1 ℃的整体温升载荷， 进行特征值求解分析. 若不考虑温度变化对材料力学性能的影响， 金属材质弹性模量Em=201 GPa， 热膨胀系数αm=12.9×10-6/℃， 陶瓷材质弹性模量Ec=380 GPa， 热膨胀系数αc=7.4×10-6/℃， 泊松比μ=0.3[10].

分别取矩形平板的厚度δ为1， 2， …， 6 mm， 平板长度a=100 mm， 宽度b=100 mm， FGM成分梯度因子k取0.5和1. 图 2 显示了不同k时平板热屈曲临界温升变化曲线， 图中点划线为式(27)的理论解， 实线为数值解. 由图 2 可以看出， 随着FGM平板厚度的增加， 临界温升逐渐增加， 且理论解与数值解基本吻合， 最大误差约为7.3%， 表明利用ANSYS有限元数值方法获得热屈曲理论解有较高的准确性.

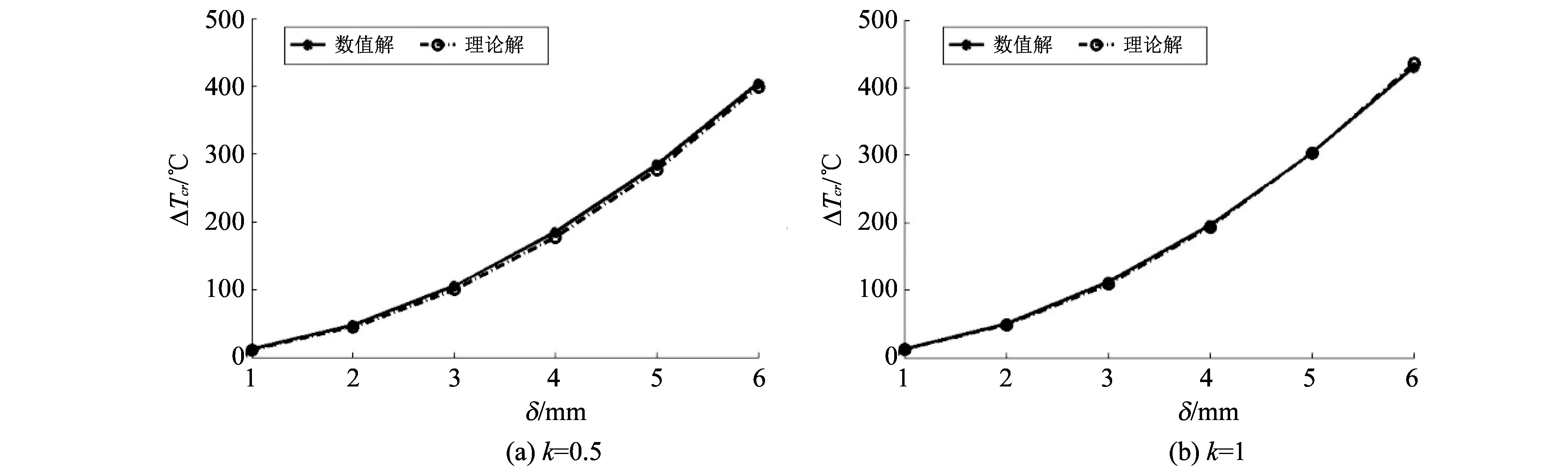
图 2 FGM矩形平板随δ变化的临界温升曲线Fig.2 Critical temperature rise of FGM rectangular plate under different δ

2.2 FGM圆筒形薄壳热屈曲行为分析

与FGM平板数值模型相似， 选用Shell281高阶单元对FGM圆筒形薄壳网格划分， 在模型上、下两端施加简支边界条件， 同时施加1℃的整体温升载荷， 材料参数与平板一致.

首先， 取FGM圆筒形薄壳半径R=500 mm， 厚径比δ/R=0.01， 长度l分别为500， 1 000， …， 3 000 mm. 图 3 显示了不同长度下FGM圆筒形薄壳热屈曲的临界温升变化曲线， 图中实线为式(21)理论解， 点划线为数值解.

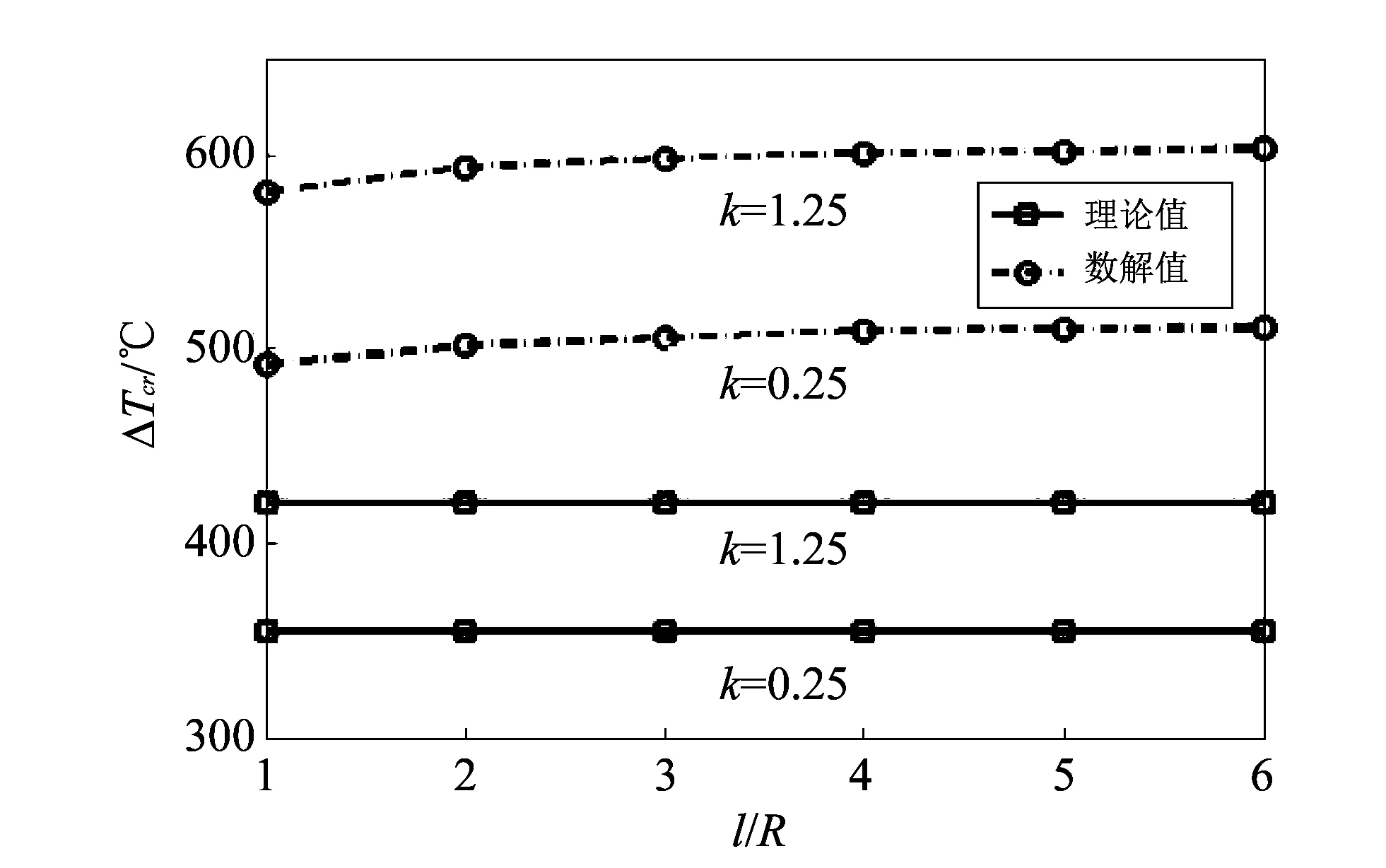
图 3 FGM圆筒形薄壳随l/R变化临界温升曲线Fig.3 Critical temperature rise of FGM thin-wall cylindrical shell under different l/R

其次， 取FGM圆筒形薄壳长度l=1 000 mm， 半径R=500 mm， 厚径比δ/R分别为0.002， 0.004， …， 0.016变化. 图 4 显示了在不同厚径比下FGM圆筒形薄壳热屈曲的临界温升变化曲线， 图中实线为式(21)理论解， 点划线为数值解. 类似取FGM圆筒形薄壳长度l=1 000 mm， 壁厚δ=5 mm， 半径R分别为200， 400， …， 1 200 mm. 图 5 显示了不同半径下FGM圆筒形薄壳热屈曲的临界温升变化曲线， 图中的实线为式(21)理论解， 点划线为数值解.

图 4 不同δ/R下FGM圆筒形薄壳的临界温升曲线Fig.4 Critical temperature rise of FGM thin-wall cylindrical shell under different δ/R

图 3 表明随着长度l的增加， 临界温升ΔTcr基本保持不变， 可见模型长度对临界温升基本没有影响； 图 4 表明随着厚径比δ/R的增加， 临界温升ΔTcr逐渐增加； 图 5 表明随着半径R的增加， 临界温升ΔTcr逐渐减少. 但是， 由图 3～图 5 可以看出， 本文推导的FGM圆筒形薄壳热屈曲理论解与ANSYS计算出的数值解存在较大误差， 结合FGM矩形薄板模型分析的结果表明， FGM圆筒形薄壳理论解存在一定的不准确性， 因此， 需要进一步分析其中的原因.

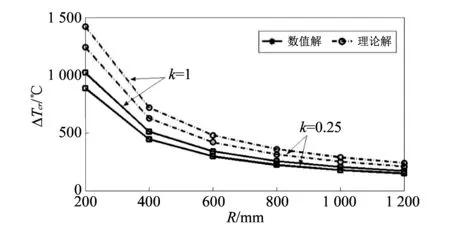
图 5 不同R下FGM圆筒形薄壳的临界温升曲线Fig.5 Critical temperature rise of FGM thin-wall cylindrical shell under different R

由图 6 可以看出， FGM圆筒形薄壳在发生屈曲变形时， 筒体不仅出现轴向波形， 还出现环向波形， 同时随着厚度的变化， 产生的波形也发生改变， 相对于平板FGM圆筒形薄壳屈曲行为更为复杂. 在利用ANSYS模拟FGM圆筒形薄壳的轴向热屈曲时， 无法排除由于环向屈曲带来的影响， 因此， 在ANSYS软件中的得到的热屈曲特征值是轴向屈曲和环向屈曲的结果. 本节基于Donnell薄壳简化准则和Timoshenko屈曲推导方法， 未考虑环向失稳波形对圆筒薄壳屈曲的影响， 因此得到的临界温升计算结果偏保守.

图 6 不同δ/R下的FGM圆筒形薄壳热屈曲云图Fig.6 Thermal buckling of FGM thin-wall cylindrical shell under different δ/R

文献[11]表明， 基于Timoshenko失稳理论， 建立圆筒形薄壳在外压载荷下的轴向失稳理论解与实验值存在一定的误差， 工程上通常采用修正系数的方法来完善理论的结果. 借用这一思想， 采用大量数据计算样本， 归纳出本节推导的FGM圆筒形薄壳热屈曲临界温升计算式修正系数C为1.41， 即式(21)变为

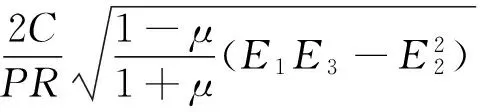
为了保证本节所提出的修正系数的正确性， 下面通过多参数对比分析来验证修正系数的正确性.

首先， 取FGM圆筒形薄壳半径R=500 mm， 厚径比δ/R=0.01， 长度l分别为500， 1 000， …， 3 000 mm， 得到在不同长度下FGM圆筒形薄壳临界温升曲线如图 7 所示， 图 7 中点划线表示理论解， 实线表示数值解， 虚线表示修正后的理论解， 可以看出， 修正后的理论解与数值解误差不到2.4%.

图 7 不同l/R下FGM圆筒形薄壳修正的临界温升曲线Fig.7 Modified critical temperature rise of FGM thin-wall cylindrical shell under different l/R

图 8 不同δ/R下FGM圆筒形薄壳修正的临界温升曲线Fig.8 Modified critical temperature rise of FGM thin-wall cylindrical shell under different δ/R

其次， 取FGM圆筒形薄壳半径R=500 mm， 长度l=1 000 mm， 厚径比δ/R分别为0.002， 0.004， …， 0.016， 得到在不同厚径比下FGM圆筒形薄壳临界温升曲线如图 8 所示， 图 8 中虚线表示理论解， 点划线表示数值解， 实线表示修正后的理论解， 可以看出， 修正后的理论解与数值解误差不到5%.

最后， 取FGM圆筒形薄壳壁厚δ=5 mm， 长度l=1 000 mm， 半径R分别为200， 400， …， 1 200 mm， 得到在不同半径下圆筒形薄壳临界温升曲线如图 9 所示， 图 9 中虚线表示理论解， 点划线表示数值解， 实线表示修正后的理论解， 且修正解与数值解误差不到1.5%， 可以看出， 修正后的理论解与数值解较为吻合， 这样就建立了FGM圆筒形薄壳结构热屈曲临界温升的精确解.

通过图 7～图 9 的对比发现， FGM圆筒形薄壳的临界温升对筒体壁厚比较敏感， 因此在工程设计时， 要在保证安全和经济的前提下， 尽量减小壁厚， 并且FGM圆筒形薄壳临界温升随着幂指数k的增加而增加. 同时， 图 7 表明， 简支条件下FGM圆筒形薄壳临界温升与长度几乎无关， 这和Timoshenko轴向失稳问题的结论比较一致.

图 9 不同R下FGM圆筒形薄壳修正的临界温升曲线Fig.9 Modified critical temperature rise of FGM thin-wall cylindrical shell under different R

3 结 论

目前， FGM平板结构在温升载荷下热屈曲临界温度理论解与数值解均比较完备， 也很统一. 但FGM圆筒形薄壳结构热屈曲临界温度理论解存在不唯一性， 且与数值解存在较大误差. 本文在FGM平板热屈曲问题分析基础上， 推导了FGM圆筒形薄壳结构在均匀温升载荷下热屈曲的临界温度理论解， 并基于有限元数值方法对理论解进行了修正， 从而给出了FGM轴对称薄壳结构热屈曲临界温度的精确解， 这将为今后类似薄壳结构工程设计提供一定的参考依据.

[1] Shariat S, Eslami M R. Buckling of thick functionally graded plates under mechanical and thermal loads[J]. Composite Structures， 2007， 78(3): 433-439.

[2] Zenkour A M， Mashat D S. Thermal buckling analysis of ceramic-metal functionally graded plates[J]. Natural Science， 2010， 2(9)： 968-978.

[3] Wu Lanhe. Thermal buckling of a simply supported moderately thick rectangular FGM plate[J]. Composite Structures， 2004， 64(2)： 211-218.

[4] 朱甚， 李四平. 横向纤维搭桥下矩形脱层热屈曲数值模拟[J]. 上海交通大学学报， 2014， 48(12)： 1784-1787.

Zhu Shen， Li Siping. Numerical simulation of thermal buckling of rectangular-shaped delamination bridged by lateral fibers in 3D composites[J]. Journal of Shanghai Jiaotong University， 2014， 48(12)： 1784-1787. (in Chinese)

[5] Yaghoobi H， Fereidoon A. Thermal buckling of axially functionally graded thin cylindrical shell[J]. Journal of Thermal Stresses， 2011， 34(12)： 1250-1270.

[6] Shahsiah R， Eslami M R. Thermal buckling of functionally graded cylindrical shell[J]. Journal of thermal stresses， 2003， 26(3)： 277-294.

[7] Lanhe W， Jiang Zhiqing, Liu Jun. Thermoelastic stability of functionally graded cylindrical shells[J]. Composite Structures， 2005， 70(1)： 60-68.

[8] 黄怀纬， 韩强， 冯能文， 等. 温度梯度下功能梯度材料圆柱壳的热屈曲[J]. 华南理工大学学报(自然科学版)， 2009, 37(6)： 101-106.

Huang Huaiwei， Han Qiang， Feng Nengwen， et al. Thermal buckling of functionally graded cylindrical shells subjected to temperature gradient[J]. Journal of South China University of Technology (Natural Science Edition)， 2009, 37(6)： 101-106. (in Chinese)

[9] 韩强. 弹塑性系统的动力屈曲和分叉[M]. 北京： 科学出版社， 2000.

[10] 高淑娟. 功能梯度材料压力容器热力耦合应力分析[D]. 大连： 大连理工大学， 2013.

[11] 郑津洋， 董其伍， 桑芝富， 等. 过程设备设计[M]. 第3版. 北京： 化学工业出版社， 2011.

TheoreticalSolutionandItsCorrectionofThermalBucklingCriticalTemperatureforFGMCylindricalThin-Shell

LI Yao-zhou1， WANG Ze-wu2

(1. Dept. of Environmental and Safety Engineering， Taiyuan Institute of Technology， Taiyuan 030008， China；2. School of Chemical Machinery and Safety, Dalian University of Technology, Dalian 116024, China)

For solving the inconsistence problem among existing theoretical solutions of the critical temperature for FGM cylindrical thin-shell, the theoretical solution of critical temperature was deduced for a FGM cylindrical thin-shell subjected to a uniform temperature rise based on Donnell equation. And then the numerical solutions of the FGM cylindrical shell were constructed separately. Lastly, by comparing analysis between the theoretical solution and numerical solution of cylindrical thin-shell under differentl/R,δ/RandR, the exact solution was obtained by introducing a modified coefficient. The results benefit to scientifically design related FGM thin-shell structures.

FGM； cylindrical shell； thermal buckling； critical temperature

1673-3193(2017)05-0561-07

2016-11-03

李耀宙(1988-)， 男， 助教， 硕士， 主要从事过程装备强度、稳定性分析和安全评估的研究.

O343.9

A

10.3969/j.issn.1673-3193.2017.05.010