顾及区域属性的不规则似大地水准面的移动窗口拼接方法

蒋光伟,郭春喜,王 斌,田晓静,聂建亮

(国家测绘地理信息局大地测量数据处理中心，陕西 西安 710054)



顾及区域属性的不规则似大地水准面的移动窗口拼接方法

蒋光伟,郭春喜,王 斌,田晓静,聂建亮

(国家测绘地理信息局大地测量数据处理中心，陕西 西安 710054)

针对我国陆地区域似大地水准面具有不等精度性与不规则性特点，提出顾及区域属性的似大地水准面移动窗口拼接算法。采用我国西南某区域的似大地水准面进行拼接试验，验证该算法可行性与可靠性。结果表明，考虑区域属性可增强拼接区域中精度相对高的控制作用，有效削弱拼接区的系统偏差，拼接精度较优于拟合拼接的方法；同时，该算法模型严密、计算效率快。

似大地水准面；拼接；移动窗口法；不规则区域

目前，我国陆地区域的高程基准现代化已广泛开展与应用，区域似大地水准面精化大都受重力数据、DEM分辨率、重力似大地水准面计算方法、GNSS/水准分布等多种因素的影响，造成不同区域似大地水准面重叠区可能存在系统偏差。理想的似大地水准面应该是对整个区域重力数据进行整体处理，形成统一的重力异常格网数据，再采用GPS水准数据对重力似大地水准面进行校正与融合。然而，相邻陆地区域似大地水准面大都是独立计算的，并与重力数据、GPS/水准分布、模型算法有着紧密的联系[1-2]；同时，基础数据的分布与区域的行政区界有着不可分割的联系，行政交接地区通常是重力数据与GPS/水准分布较少的区域，这使似大地水准面在基础数据分布密度稠地区精度相对较高，从而在区域边界具有不等精度的特点。因此，似大地水准面拼接必须控制和削弱不同区域似大地水准面间的系统偏差影响，保证拼接后的似大地水准面满足位理论的要求，使拼接区不存在明显的区域性差异，从而真实反应似大地水准面的起伏状况。

似大地水准面的拼接研究主要为陆海区域的似大地水准面拼接，拼接方法：解析法、最小二乘频谱组合法、迭代FFT法、最小二乘配置法、拟合拼接法等[3]。相关学者对引起陆海区域似大地水准面的系统差进行分析与研究：陈俊勇等[4]提出我国陆海交界处陆海似大地水准面拼接的原则；李建成等[5]结合我国陆海拼接区域重力资料稀疏的情况，提出扩展拼接的方法；曾传俊等研究产生陆海似大地水准面拼接差的原因，提出基于拟合方法的无缝拼接的方法；鞠晓蕾[6]研究不同密度数据源的区域性陆海似大地水准面，采用最小二乘配置的方法进行拼接。目前，似大地水准面拼接主要针对陆海区域，较少研究陆地区域似大地水准面拼接。结合陆地区域已有似大地水准面具有的不等精度性、不规则性特点，重点研究陆地区域似大地水准面的拼接问题。笔者提出顾及区域属性的不规则似大地水准面的移动窗口拼接法。该算法首先基于相邻重叠区域的不规则边界生成一定范围的拼接区格网；其次基于区域属性采用不等权的算法对拼接区进行平滑；最后进行不规则区域似大地水准面格网的替换。

1 基准统一

似大地水准面精化过程中，各区域计算可能采用不同的坐标系统，如CGCS2000、1980西安坐标系，高程基准采用的是1985国家高程基准，有些区域采用ITRF框架瞬时历元的结果。实现已有陆地区域似大地水准面成果的拼接，需要将成果统一到相同的框架与历元。

似大地水准面计算涉及重力数据、地形数据、重力场参考模型、积分半径、地形改正、GPS水准数据，这些基础数据都存在基准的统一。因此，区域似大地水准面拼接首先消除由起算基准的不一致性引起的系统差。

2 拟合拼接法

拟合拼接算法的实质是利用拼接区的高程异常差值序列，采用数学模型进行纠正。该方法保持非拼接区域似大地水准面不变，对拼接区域进行平滑削弱系统偏差与其他随机误差的影响。该方法的不足之处在于没有考虑似大地水准面的区域属性，拼接区一般是重力数据与GPS水准数据分布较少的区域，采用拟合拼接方法可能会使拼接区似大地水准面产生较大的误差。由于拟合方法的差异对拼接的效果也不同，采用最小二乘配置法，该方法能较好地解决含有倾向性、随机性因素的问题，适宜于削弱不符值中系统误差的影响。

最小二乘配置法模型(Collocation，CO)为

ζ=AX+BS+Δ.

(1)

式中：ζ为n个拼接区格网点对应的差异值；A，B表示倾向性参数以及信号参数对应的系数矩阵；Δ为观测误差向量；X为倾向性参数向量；S为信号向量。

最小二乘估计值与信号估计值分别为

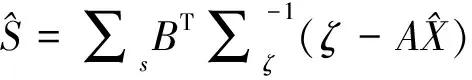
(2)

其中

∑ζ=B∑SBT+∑Δ.

(3)

式中：S′未测点的信号；∑S′S为已知点与未知点差异的互协方差矩阵；∑Δ为观测噪声的协方差矩阵；∑S为信号的协方差矩阵；∑ζ为自由项ζ的协方差矩阵。

3 顾及区域属性的移动窗口拼接法

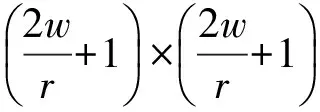
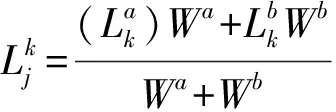
(4)

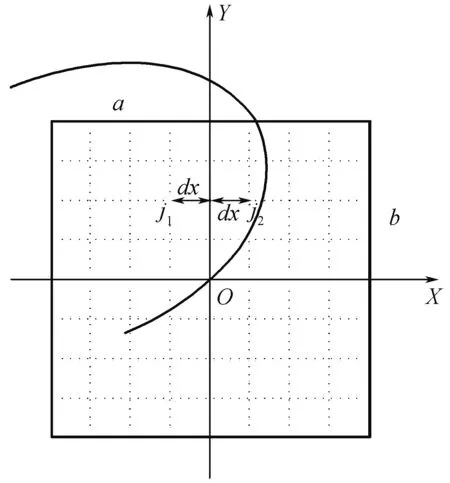
图1 任一格网点区域分布

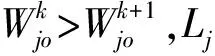
6) 返回到步骤(1)进行下一窗口循环，计算截止到区域边界线最后一点。

4 试验与分析

为验证该方法的可行性与适用性，搜集我国西南地形复杂某区域的重力数据与GPS水准数据，统一基准使用顾及地形影响的重力水准法计算似大地水准面。首先，采用整体法(Regional Integral Compute, RIC)计算区域的统一似大地水准面。其次，将区域分为两个不规则子区域分别计算两区域似大地水准面。整体计算的似大地水准面在平原丘陵地区精度为±2.1 cm、山地为±7.2 cm。文中设计两种方案对比最小二乘配置法与顾及区域属性的移动窗口法在不规则区域、不等精度似大地水准面拼接中的差异。为检验拼接算法的可靠性，在两区域拼接区空出21个检核点(见图2)。图2中，加粗线为两区域的重合边界线，拼接区为边界线两侧10 km的区域。

方案1：采用等精度的重力似大地水准面，两区域与整区域都采用重力场模型积分半径为30 km、地形改正为40 km的重力似大地水准面，使用最小二乘配置法与顾及区域属性的移动窗口法进行似大地水准面的拼接，见图3。

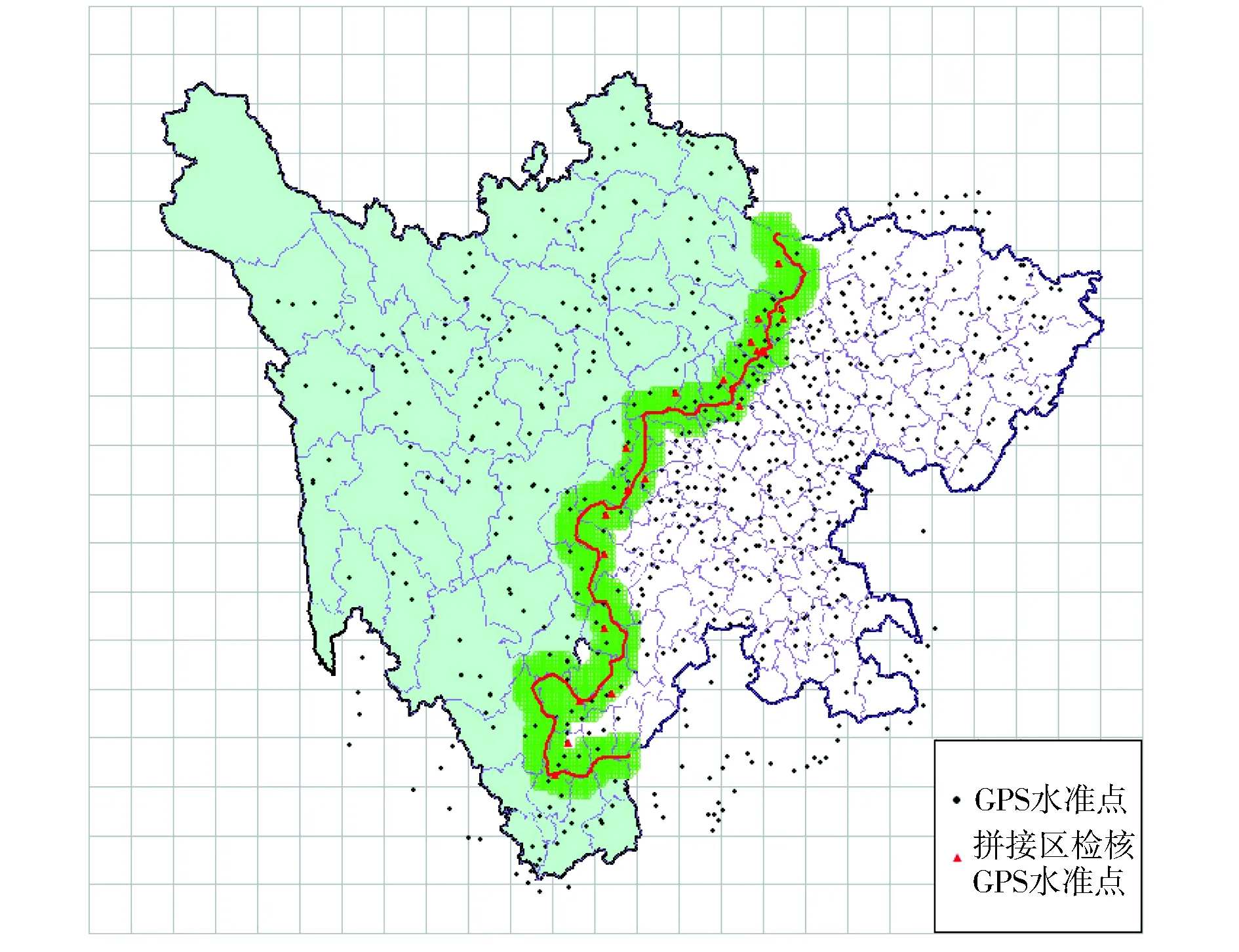
图2 区域GPS水准点位分布

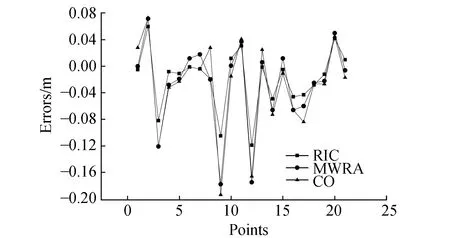
图3 方案1空点残差

方案2：采用不等精度的重力似大地水准面，两区域与整区域的重力似大地水准采用不同积分半径的重力场模型与地形改正。使用最小二乘配置法与顾及区域属性的移动窗口法进行两不规则区域似大地水准面的拼接。算例中两区域重力场模型积分半径分别为15 km，25 km，地形改正模型积分半径分别为20 km，95 km，整区域重力似大地水准面计算与方案1相同，见图4及表1。

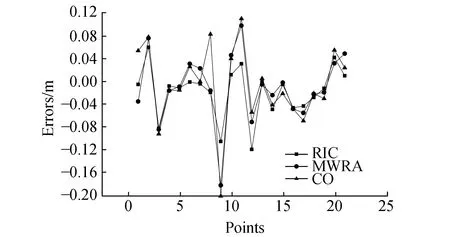
图4 方案2 空点残差

综合结果得到结论：

1)顾及区域属性的移动窗口拼接法一定程度上削弱了似大地水准面在接边处的系统偏差，增强了已有似大地水准面拼接成果的连续性。

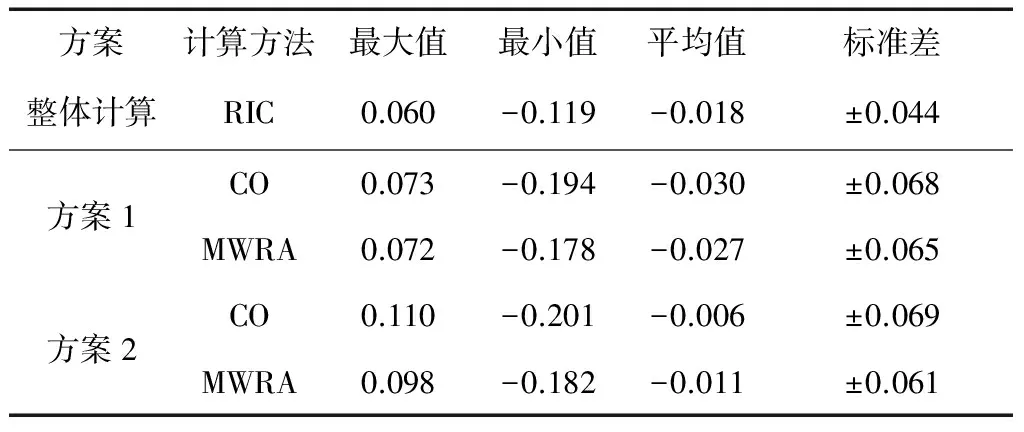
表1 拼接区实测值高程异常与真实高程异常对比 m

2)从实测检核点残差分布可明显得出：整体计算方法不存在拼接区且精度最高。在拼接区域中，整体法计算的似大地水准面残差的标准差、最大值、最小值都优于最小二乘配置与顾及区域属性的移动窗口拼接法的结果。

3)从两种方案结果可以得出：MWRA与CO都可以获取较高精度的拼接结果；MWRA拼接区域的检核点标准差小于CO方法获取的，且MWRA检核点残差值都较优于CO的结果。

4)MWRA与CO拟合拼接法在方案1中，差异较少，在方案2中，差异较大。MWRA获取的拼接区域的似大地水准面精度提高8 mm，部分检核点残差提高近2 cm。因此，MWRA算法更适合不等精度的区域似大地水准面拼接。

5)MWRA算法严密，非近似的以对称轴的上下或者左右来划分区域，考虑区域权属性的对称性，因此该方法能使基础数据分布多、精度相对高的似大地水准面在拼接区中具有较大的权重，进一步增强精度高的控制作用；拟合拼接法没有考虑拼接区域属性，且观测值权相同，不能增强精度相对高区域的控制作用，拟合方法易使拼接区似大地水准面格网出现异常，从而改变似大地水准面起伏的真实性。

6)从算法的模型上可得出：MWRA算法是对应格网的加权平均值，计算效率快、精度较高；拟合拼接算法存在超大型矩阵的求逆运算，计算效率慢，大型矩阵运算可能会造成矩阵病态，将影响拼接结果的可靠性。

5 结束语

本文从我国陆地区域似大地水准面不规则性与不等精度性出发，引入区域属性的判断条件，提出了顾及区域属性的似大地水准面的移动窗口拼接方法。通过与最小二乘配置拟合拼接的试验与分析，验证了该方法的有效性与可靠性；计算结果表明该算法严密，计算效率快，可进一步增强似大地水准面精度相对高区域的控制作用；该方法在拼接区域精度稍优于拟合拼接的方法。

文中方法主要针对陆地区域的似大地水准面模型的拼接，然而实际的GPS水准点分布、拟合方法对重力似大地水准面的校正，都有可能改变似大地水准面在区域交接处的趋势。因此，后期主要研究重力似大地水准面的拼接。

[1] 李建成.最新中国陆地数字高程基准模型：重力似大地水准面CNGG2011[J].测绘学报,2012,41(5):651-660.

[2] 章传银,党亚民,柯宝贵,等.高精度海岸带重力似大地水准面的若干问题讨论[J].测绘学报,2012,41(5):709-714.

[3] 曾传俊,姚宜斌,高波.中国陆海大地水准面拼接问题的理论探讨[J].测绘信息与工程,2008,33(5):17-19.

[4] 陈俊勇,李建成,宁津生,等. 全国及部分省市地区高精度、高分辨率大地水准面的研究及其实施[J].武汉大学学报(信息科学版),2006,31(4):283-288.

[5] 李建成,宁津生,陈俊勇,等.我国海域大地水准面与陆地大地水准面的拼接研究[J].武汉大学学报(信息科学版),2003,28(5):542-546.

[6] 鞠晓蕾.区域性陆海大地水准面拼接研究[D].山东：山东科技大学,2011.

[7] 郭春喜,聂建亮,王斌,等.区域似大地水准面拟合方法及适用性分析[J].大地测量与地球动力学,2013,33(1):103-107.

[8] 石平,裴志刚,娄中军.贵阳市似大地水准面精化项目建设[J].测绘与空间地理信息，2016,39(4)：194-196.

[9] 罗文生,邱云峰,杨忠祥.加权组合模型在区域似大地水准面精化中的应用研究[J].测绘与空间地理信息，2016,39(4)：197-200.

[10] 郭春喜,蒋光伟,聂建亮,等.抗差自适应拟合推估技术在似大地水准面拟合中的应用[J].测绘工程,2014,23(3):1-4.

[11] 杨元喜,张菊清,张亮. 基于方差分量估计的拟合推估及其在GIS误差纠正中的应用[J].测绘学报,2008,37(2):152-157.

[12] 欧阳永忠,邓凯亮,黄谟涛,等.确定大地水准面的Tikhonov最小二乘配置法[J].测绘学报,2012,41(6):804-810.

[责任编辑：李铭娜]

The move window algorithm of merging irregularquasi-geoid based on the regional attribute

JIANG Guangwei,GUO Chunxi,WANG Bin, TIAN Xiaojing, NIE Jianliang

(Center for Geodetic Data Processing,National Administration of Surveying,Mapping and Geoinformation,Xi’an 710054,China)

Because the regional land quasi-geoid has the irregular and unequal precision, this paper proposes a new move window method to merge the quasi-geoid, which takes into account the regional attribute. Taking the southwest China region’s quasi-geoid as the case, this paper demonstrates the feasibility and reliability of the method, and the results indicate that, the algorithm can enhance the control effect of relative high precision quasi-geoid, and effectively weaken the systematic errors. The merging accuracy is better than the fitting method while the algorithm model is rigorous and fast in computional efficiency.

quasi-geoid;merging;move window algorithm;irregular region

10.19349/j.cnki.issn1006-7949.2017.03.004

2015-12-07

国家863资助项目(2009AA121402-5)；2015年测绘地理信息公益性行业科研专项(201512004)

蒋光伟(1985-)，男，硕士.

P223

A

1006-7949(2017)03-0019-04

引用著录：蒋光伟,郭春喜,王斌，等.顾及区域属性的不规则似大地水准面的移动窗口拼接方法[J].测绘工程，2017，26(3)：19-22.