一种基于平面不等式约束法的北斗三频数据组合选取方法
2017-12-22张建龙
张建龙,丰 勇,隋 心
(1.黑龙江煤炭职业技术学院 资源环境工程系,黑龙江 双鸭山 155100; 2.辽宁省测绘地理信息局 辽宁 沈阳 110804;3.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)
一种基于平面不等式约束法的北斗三频数据组合选取方法
张建龙1,丰 勇2,隋 心3
(1.黑龙江煤炭职业技术学院 资源环境工程系,黑龙江 双鸭山 155100; 2.辽宁省测绘地理信息局 辽宁 沈阳 110804;3.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)
GNSS现代化的标志之一是三频或多频数据的广泛使用,文中在研究北斗三频数据组合原理、优化选取准则的基础上,推导出一种基于平面不等式约束法的三频数据组合选取方法。该方法将长波长条件转化为组合系数的线性关系,将弱电离层条件转化为平面域,将低噪声条件转化为椭圆域,依此建立模型并给出模型的几何解释,最后应用该方法选取特性较优的北斗三频数据组合,并总结了一些组合系数的特点。结果证明,该方法组合系数选取效率大于枚举法等常规方法,从而为多频数据组合理论的研究提供参考。
北斗系统;三频数据组合;平面不等式约束法; 平面域;椭圆域
伴随着GNSS现代化进程,各国导航系统为了抢占市场都增加了多个频率信号的建设,我国北斗二代系统采用B1、B2、B3 3个频率。多频数据能形成更多长波长、低噪声、弱电离层延迟等特性优良的组合,因而在周跳探测与修复、模糊度快速固定等方面应用广泛。多频数据的使用为导航定位关键技术的解决带来了新机遇,同时也衍生出适应于多频数据处理的算法[1]。
本文在研究北斗三频数据组合理论的基础上,基于优化选取原则,结合椭圆方程,推导出一种基于平面不等式约束法的组合系数选取法,给出了图形的几何解释,并结合程序优化选取了特性较优的部分组合。
1 北斗三频数据组合
1.1 数据组合原理
三频载波相位组合是在载波相位观测方程基础上进行线性组合形成的,设某历元下GNSS接收机捕获的各频点载波相位观测方程为[2]
Li=λiφi=ρ+c(dT-dt)-λiNi-
(Vion)i-(Vtrop)i+δdorb+Mi+εi.
(1)
式中:i=1,2,3为3个载波;λ为波长;φ为载波相位观测量;ρ为卫星至接收机的几何距离;c为真空中光速(2.997 924 58×108m/s);dT为卫星钟差;dt为接收机钟差;N为整周模糊度;Vion为电离层延迟影响;Vtrop为对流层延迟影响;δdorb为轨道误差影响;M为多路径影响;ε为观测噪声。则组合观测值为[3-5]
Lcom=λcφc=pL1+qL2+rL3.
(2)
若要保证组合后测站与卫星间距离不发生变化,3个组合系数p,q,r需满足
p+q+r=1.
(3)
代入式(2)可写为
λcNc-ξ(Vion)1+Mc+ec.
(4)
其中:
λcNc=pλ1N1+qλ2N2+rλ3N3,
ξ=p+qα+rβ,
Mc=pM1+qM2+rM3,
ec=pe1+qe2+re3.
一般要求组合后模糊度仍然保留整数特性,以便于模糊度正确固定,即
Nc=lN1+mN2+nN3.
(5)
式中,l,m,n为整数。最终求得组合波长
(6)
组合频率
fc=lf1+mf2+nf3.
(7)
组合相位
φc=lφ1+mφ2+nφ3.
(8)
1.2 组合值误差影响
这里仅分析与优化选取有关的一些误差影响如电离层、噪声,而对流层、轨道误差、卫星钟差及接收机钟差都是与频率无关的量,组合前后误差影响不发生变化。组合后电离层误差影响为[6-7]
(9)
可见组合系数的选取将直接影响组合观测值电离层延迟误差大小,经过合理选取后的组合系数可以使得组合观测值电离层延迟达到相对较小的要求。
各频点噪声相同σLi=σL(i=1,2,3),则组合观测值以米为单位的噪声
(10)
1.3 优化选取准则
从数学角度看组合系数有无穷多组,但要从中选出有利于周跳探测、模糊度固定、提高定位精度的组合就大大减少了。对于组合观测值的选取通常有如下一些选取准则:组合值应保持整数特性以利于确定整周模糊度;组合值应具有较长的波长;组合值应降低电离层误差的影响;组合值受到的噪声影响应尽量小。
对北斗系统要满足组合观测值具有较长波长的要求就是要使得组合波长λc满足λc>λ2,由此可确定m的取值范围为
(lλ2/λ1+nλ2/λ3) 1-(lλ2/λ1+nλ2/λ3). (11) 不难发现整数m在l和n确定后是唯一存在的,考虑到组合系数还要满足式(10),故l和n不宜太大,否则组合值噪声将会被放大。采用式(12)来对比组合波长与原始载波的比率关系 (12) 为了减小电离层的影响,组合后电离层误差影响Δ(Vion)L-com应尽量小。采用式(13)来对比组合值电离层影响与B1频点上电离层影响的比率关系 (13) 为了使组合值噪声尽量小,组合观测值以米为单位的噪声要求满足σL-com<σL,即满足式(14)。 (14) 2.1 模型的建立 只有同时满足了上面3个条件的组合系数才是最优组合系数,对于优化组合系数的选取,比较简单的办法是采用枚举法,但该方法计算量较大,计算效率较低。研究人员开始考虑采用其他方法提高组合系数选取效率,文献[8]对北斗三频数据线性组合进行了优化分析。文献[9]采用整数规划法,以组合观测值的波长为目标函数,以弱电离层和弱噪声为约束条件建立模型;文献[10]采用模糊聚类法。但这些方法模型建立过程比较复杂。 若对长波长约束条件式(11)观察可以发现,尽管含有3个变量,但m与l和n相关,因此实际上仅有两个变量,是一个二维平面上的不等式约束问题。在弱电离层条件约束下,式(13)可以给定一个较小的取值范围。在低噪声条件约束下,式(14)是一个椭圆域。由以上两个条件再把取值限定为整数,即可确定符合条件的组合系数。下面进行推导: 由式(11)可知,m可以表示为l和n的线性表达式 m=k1l+k2n+b. (15) (16) 即 -ν0f2f3≤(f2f3+k1f1f3)l+(k2f1f3+ f1f2)n+bf1f3≤ν0f2f3. (17) 这是一个关于l和n所表示两条直线形成的平面区域。式(14)化简为 (18) 即 (19) 为了便于理解,这里引入椭圆方程的知识,现引述如下。椭圆一般方程为 Ax2+Bxy+Cy2+Dx+Ey+F=0. (20) 椭圆标准方程为 (21) 式(20)变形为 A(x-x0)2+B(x-x0)(y-y0)+ C(y-y0)2+f=0. (22) 令x′=x-x0,y′=y-y0,则有 Ax′2+Bx′y′+Cy′2+f=0. (23) 式(21)中,令x=x′cosθ-y′sinθ,y=x′sinθ+y′cosθ。 代入式(21)有 (24) 化简式(24)并与式(23)对比各项系数有 (25) 最后求得 (26) 式中,a,b分别为椭圆长半轴和短半轴。 椭圆中心为 (27) 长半轴倾角为 (28) 这里看出式(19)表示的是一个椭圆域,其椭圆的两个半轴长为 椭圆中心为 两直线为 1.029l+0.196n+1.53ν0-1.98b≥0, 1.029l+0.196n-1.53ν0-1.98b≤0. 2.2 模型的几何解释 通过2.1节的分析,由式(17)和式(19)所组成的范围是两条直线和一个椭圆所确定的平面区域,如图1所示。从图1看出只有落在椭圆内部或其附近及两条直线内侧的点才是符合优化条件的组合,这是对噪声及电离层延迟量约束的直观显示。凡是距离椭圆比较远的点,即使在直线内侧也不一定满足优化条件。如果给出的ν0太大,也就是说两条直线远离椭圆,会造成电离层放大倍数太大,同样不符合条件。选取过程中,可用一条平行n轴的直线至左向右逐步搜索,这样选出特性较优组合的效率要大于枚举法。 图1 不等式约束条件确定的区域 根据相关文献,组合波长在0.75 m与2.93 m之间为宽巷组合,波长大于2.93 m为超宽巷组合,本文以l∈[-15,15],n∈[-15,15]为范围,基于上面提出的方法进行实验验证。如表1所示求取了部分北斗三频组合系数及参数。 通过组合系数的求取可以发现组合系数具有如下特点: 1)分布在取值范围边界的组合电离层和噪声都比较大,有些组合电离层扩大倍数甚至达到数百倍,噪声也达到分米级,往往不满足最优组合条件。 2)分布在取值范围中间的组合值多具有同时满足3个条件的特性,说明组合系数绝对值不宜过大。 3)组合系数和为零的组合电离层及噪声都比较小。 表1 北斗三频组合系数及参数 三频数据组合在周跳探测、模糊度快速解算等方面有着广泛的应用,也是这些算法建立过程中选取优化组合系数的基础[11]。本文从相位组合的定义出发分析了组合后的各项误差特性,将长波长条件表示为组合系数的线性关系,利用直线方程和椭圆方程对优选条件进行综合分析,建立了一种新的数据组合选取方法。本文提出的平面不等式约束法是第3节所总结特点的直观化表示,是一种有效的三频数据选取方法,从而为北斗导航系统数据处理方法研究提供了一些参考。 [1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6. [2] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2010. [3] 黄令勇.GNSS多频数据处理理论与方法研究[D].郑州:信息工程大学,2012. [4] 王泽民,柳景斌.Galileo卫星定位系统相位组合观测值的模型研究[J].武汉大学学报(信息科学版),2003,28(6):723-727. [5] 刘旭春,伍岳,黄学斌,等.多频组合数据在原始载波观测值预处理中的应用[J].测绘通报,2007(2):14-17. [6] 郭忠臣,高井祥,王坚,等.GNSS多频观测值线性组合研究[J].大地测量与地球动力学,2015,35(3):379-382. [7] 徐军,陶庭叶,高飞.GLONASS三种载波频率组合值研究[J].大地测量与地球动力学,2013,33(1):86-89. [8] 刘国超,黄张裕,徐秀杰,等.北斗三频数据线性组合优化分析[J].测绘科学,2015,40(10):69-73. [9] 陈宇,白征东,原波.整数规划在三频组合观测值确定中的应用[J].大地测量与地球动力学,2010,30(6):116-119. [10] 邢喆,王泽民,伍岳.利用模糊聚类方法筛选GPS载波相位组合观测值[J].武汉大学学报(信息科学版),2006,31(1):23-26. [11] 黄令勇,翟国君,欧阳永忠,等.三频GNSS电离层周跳处理[J].测绘学报,2015,44(7):717-725. [责任编辑:刘文霞] A new BDS triple-frequency data combination selection method based on planar inequality constraints rules ZHANG Jianlong1,FENG Yong2,SUI Xin3 (1.Dept. of Resources and Environment Engineering, Heilongjiang Coal Vocational and Technical College, Shuangyashan 155100, China;2.Liaoning Province Geographic Information Bureau of Surveying and Mapping, Shenyang 110804, China; 3.School of Geomatics, Liaoning Technical University, Fuxin 123000, China) One symbol of GNSS modernization is the widespread use of triple-frequency or multi-frequency data. The paper proposes a method based on planar inequality constraints triple-frequency data selection method with the study of BeiDou triple-frequency data combination principle and optimization selection criterion. In this paper, the long wavelength condition is transformed into the linear relationship of combination coefficients, the week ionosphere condition is conversed into surface domain, and low noise condition is changed into elliptic domain. The model is established, and geometric interpretation of the model is given. Finally it selects BeiDou triple-frequency data combination with better characteristic according to this method and summarizes some characteristics of combination coefficient. The results prove that selection efficiency of this method is better than conventional methods such as enumeration method. Thus this method provides some reference for the research of multi-frequency data combination theory. BeiDou Satellite Navigation System(BDS);triple-frequency data combination; planar inequality constraints rules;surface domain;elliptic domain 10.19349/j.cnki.issn1006-7949.2017.03.006 2016-04-24 地理空间信息工程国家测绘地理信息局重点实验室经费资助项目(201522) 张建龙(1987-),男,助理讲师,硕士研究生. P228 A 1006-7949(2017)03-0028-04 引用著录:张建龙,丰 勇,隋 心.一种基于平面不等式约束法的北斗三频数据组合选取方法[J].测绘工程,2017,26(3):28-31,36.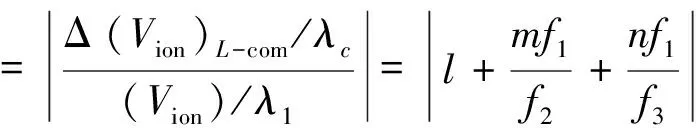
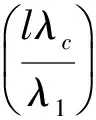
2 基于平面不等式约束法的组合系数选取法
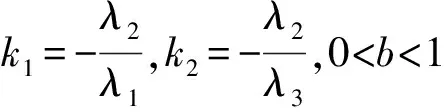

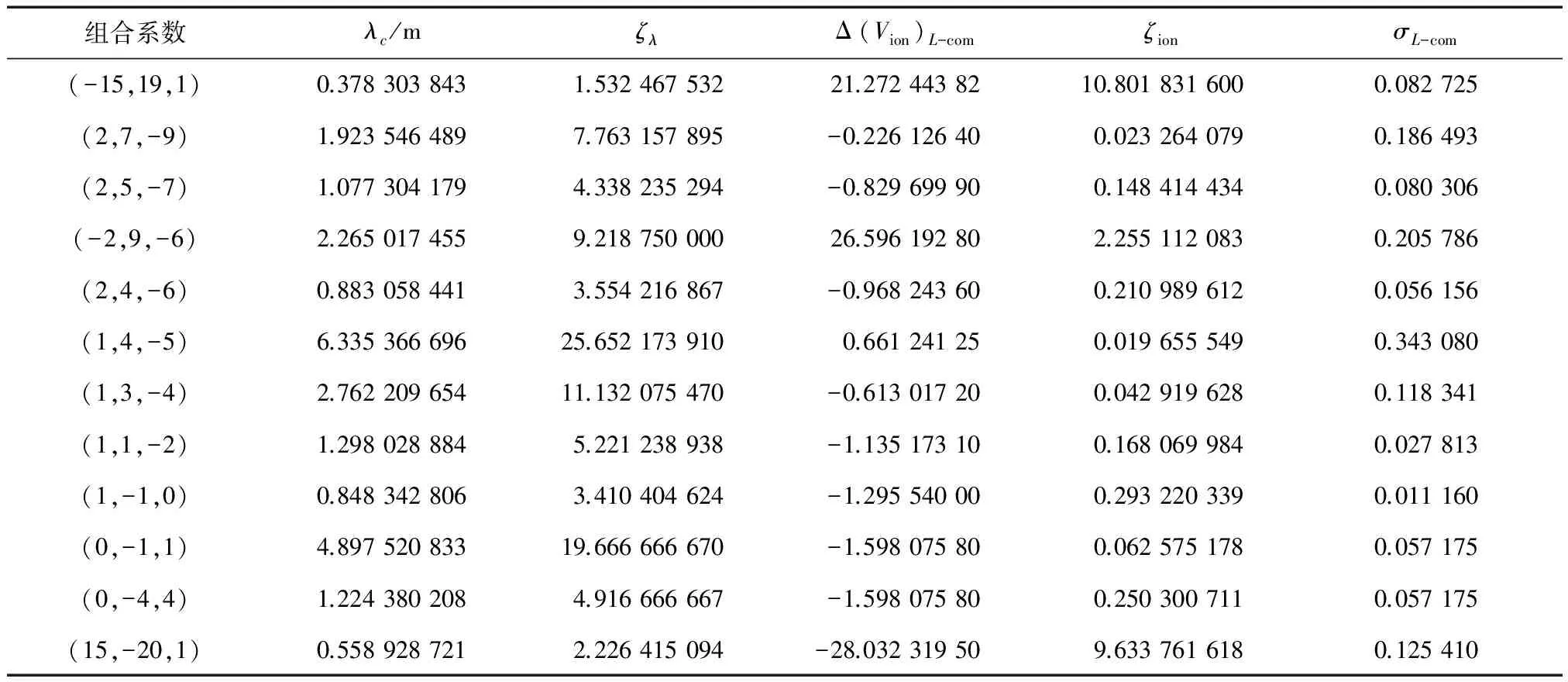
3 组合系数的选取
4 结 论
