小波分析在垂向海潮特征信息去噪研究

陈 运，吴志露，何丽娜，2

(1.河海大学 地球科学与工程学院，江苏 南京 211100;2.地理信息工程国家重点实验室，陕西 西安 710054)



小波分析在垂向海潮特征信息去噪研究

陈 运1，吴志露1，何丽娜1，2

(1.河海大学 地球科学与工程学院，江苏 南京 211100;2.地理信息工程国家重点实验室，陕西 西安 710054)

目前国内外许多学者利用沿海GPS站点的高精度坐标时间序列进行海潮特征信息的提取研究，已取得一定成果，但高精度坐标时间序列中不可避免地存在许多噪声，极大影响海潮特征信息的提取。基于日本GMSD站的67 d的高精度PPP坐标时间序列，利用小波分析进行去噪实验，经FFT变换后，将提取的结果与FES2004海潮模型的特征值比较。实验结果表明：经小波分析后，GPS站点的时间序列精度得到提高；经小波去噪后的反演精度均有不同程度的提高，最多达到0.14 mm，而海潮特征值的量级为厘米级或者亚厘米级，说明小波分析对海潮特征值的提取精度有明显提高。

小波分析；时间序列；PPP；海潮特征信息；FFT

近年来，GPS技术发展日趋成熟，定位精度也越来越高，高精度的GPS技术逐渐应用于地球板块运动、地壳形变监测、海平面变化监测和地球框架的构建等高精度领域[1-2]。

海潮负荷是进行精密单点定位(Precise Point Positioning，PPP)不可忽略的误差源，在沿海区域进行高精度单点定位时需考虑。但同时，海潮负荷是海洋科学中重要的信息，可反映海洋潮汐的一些重要信息。不加入海潮改正的GPS精密单点定位坐标时间序列中包含有海潮信息，通过频谱分析可将海潮特征信息提取出来，从而达到对潮汐观测的目的，目前已有多位专家学者进行相关领域研究[3-6]。然而在高精度坐标时间序列中不可避免的存在着许多噪声，这些噪声无疑将影响坐标时间序列的精度以及对时间序列的进一步分析。小波分析具有良好的时频局部性，目前已经被广泛应用于形变分析中，并取得较好的结果[7-8]，是国际上极为活跃的研究方向[9]。通过小波变换可对信号的不同频率成分进行分解，可将时间序列中高频噪声去除，提高反演精度。

本文基于GMSD两个月的高精度PPP坐标时间序列，利用小波分析对时间序列进行去噪。海潮对于GPS定位影响主要集中在高程方向，故本文只对高程方向进行研究分析。

1 小波分析的基本理论及去噪模型

1.1 小波分析的基本理论

小波分析是20世纪80年代中期由傅里叶变换发展而来的一种时频分析方法，性能较傅里叶变换更加优越，可以根据频率的高低自动调节窗口大小，具有多频率分析功能，目前已广泛应用于调和分析、话音处理、图像分割等[10]。

小波分析的基本思想是基于小波函数去表达或者逼近一个信号或者函数。对于任意信号函数f(x)，其小波变换定义为

ωf(a,b)=∫Rf(x)ψ(a,b)(x)dx=

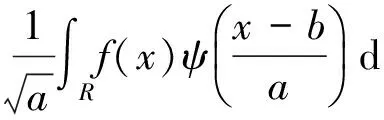
(1)

式中：a为尺度因子；b为时间平移因子；ψ(a,b)为小波母函数。

1.2 小波去噪模型

小波分析应用主要是进行信号去噪，含有噪声的一维信号：

s(k)=f(k)+ε·e(k)，k=0,1,…,n-1.

(2)

式中：s(k)为原始信号，f(k)为有用信号，e(k)为噪声信号，ε为噪声系数的标准差。

观测序列中有用信号与噪声在频率域特征通常是不同的：有用信号在时域和频域上是局部化的，表现为低频特性或较为平稳的信号；而噪声在时频空间中的分布是全局性的，存在于整个观测时域内，故在频域上表现为高频信号。小波分析在时域和频域同时具有良好的局部化性质，可分离高频与低频信号，通过小波分析消除高频噪声，保留低频有用信息。

对原始数据进行小波分析有3个步骤：

1)小波分解。根据具体问题与性质选择合适的小波函数及其分解层次f，并对原始数s(k)进行f层分解。对于分解的层次的选择，应根据信号变化情况以及数据采样率，当信号波动性较强而采样数点过稀时，过高的分解层次会对信号中确定性现象进行过滤，引起信号恢复时的失真。一般情况下，3层或4层分解即可获得较好结果。

2)对小波分解的高频系数进行处理。通过小波分解将真实信号与噪声信号最大程度分离，最终达到削弱甚至消除噪声误差的影响。进行阈值去噪时，阈值的选择有多种，可根据不同的分解目的选择不同的阈值，进行软阈值和硬阈值处理，硬阈值处理后信号比软阈值处理后的信号较为粗糙。

3)信号重构。将小波分解的第f层低频信号与经过阈值处理之后的1～f层的高频系数进行重构，可得到消除噪声之后的观测时间序列估计值。

2 海潮反演模型

潮汐现象可视为由多个周期、振幅各异的分潮组成，按周期大致分为3类：①半日潮，如M2,N2,K2,S2分潮；②全日潮，如K1,P1,Q1,O1分潮；③长周期分潮，如Ssa,Sa,Msf等[11]。本文只对其中8种短期分潮进行研究，其周期如表1所示。

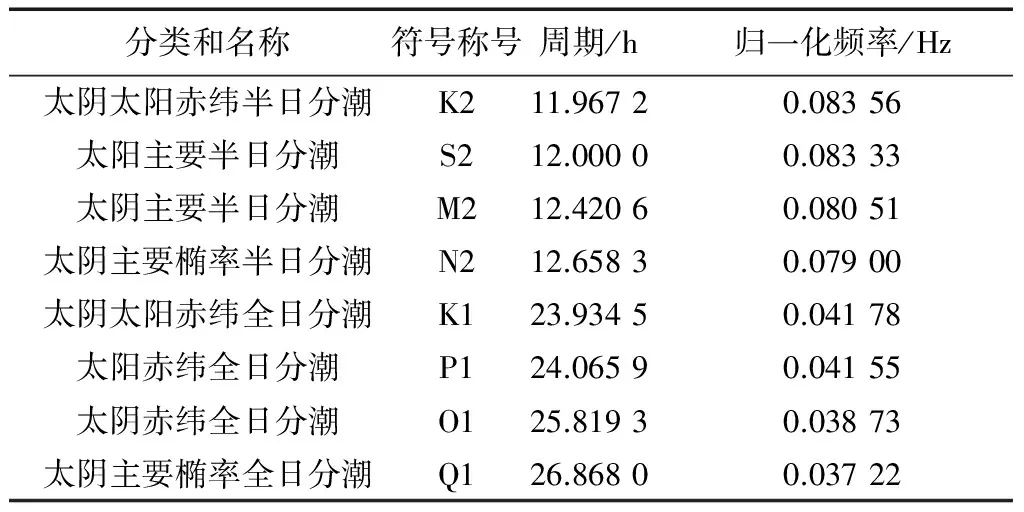
表1 短周期分潮的周期

海潮负荷主要由这8种不同频率谐波组成，其数学式可表达为

).

(3)

式中：Δj(j=1，2，3)分别为观测站N向、E向和U向的海潮负荷变形；Φk,j和Ak,j为对应分潮的初始相位和振幅；ωj为对应分潮的角速度。

在不加入海潮负荷改正的坐标时间序列中，假如对其他误差源进行较好抑制与消除，时间序列中主要包含的信息将为海潮负荷信息，此时利用频谱分析手段对坐标时间序列进行分析，将得到海潮负荷的振幅与相位，即海潮的特征值。快速傅里叶变换(Fast Fourier Transform，FFT)主要应用于离散数据在计算机上快速获取信号频域特征，借助MATLAB仿真平台，利用FFT对坐标时间序列进行海潮负荷提取的研究。

3 实验结果与分析

本文选取的GPS站点为日本的GMSD站，采样时间为2014年年积日189～243，共67 d，采样频率为30 s，借助PPP解算软件的动态模块解算(不加入海潮改正)。卫星精密星历与钟差采用IGS提供的最终精密轨道(15 min)和精密钟差(30 s)，将IGS提供的GMSD坐标为真实值，输出站心坐标(N、E、U)，最终输出67 d高精度垂向时间序列，结果如图1所示。

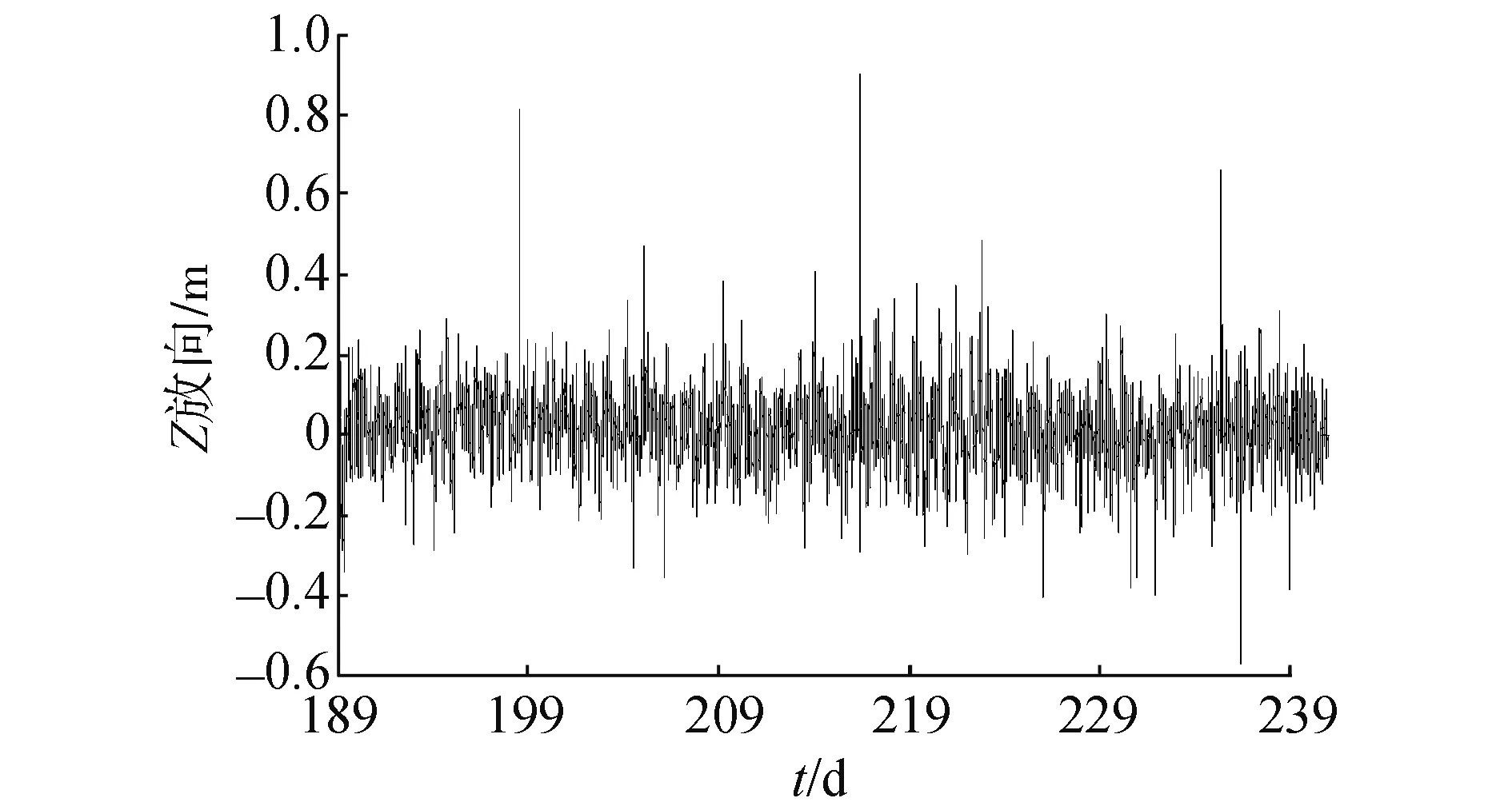
图1 GMSD站U方向的变化

Daubechies小波基具有紧支集正交，由于它具有良好的时频分析性能， 目前已在许多工程领域中得到应用。因此，本文分析考虑采用Daubechies小波，经小波分析之后时间序列如图2所示。

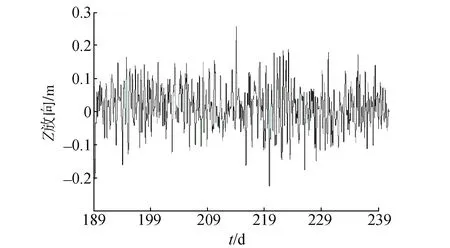
图2 小波去噪后GMSD站U三个方向的变化

对去噪前后的时间序列进行统计分析，原始时间序列高程方向中误差由7.86 cm降低为6.32 cm，精度提高1.5 cm；此外，从图1、图2中可知，一些毛刺得到很好的抑制，说明小波分析可提高时间序列的精度。

对滤波前后的时间序列进行FFT变换，频谱分析结果如图3、图4所示。海潮负荷8种分潮的频率分布在0.4 Hz与0.8 Hz附近。图3、图4中目标信号非常明显，说明基于精密坐标时间序列提取海潮分潮特征信息是可行的。同时，比较两种时间序列的频谱结果，经过小波分析后，大部分高频噪声都被消除或者抑制，低频有用的目标信号得到了保留。

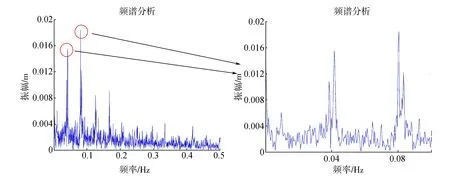
图3 原始时间序列频谱结果

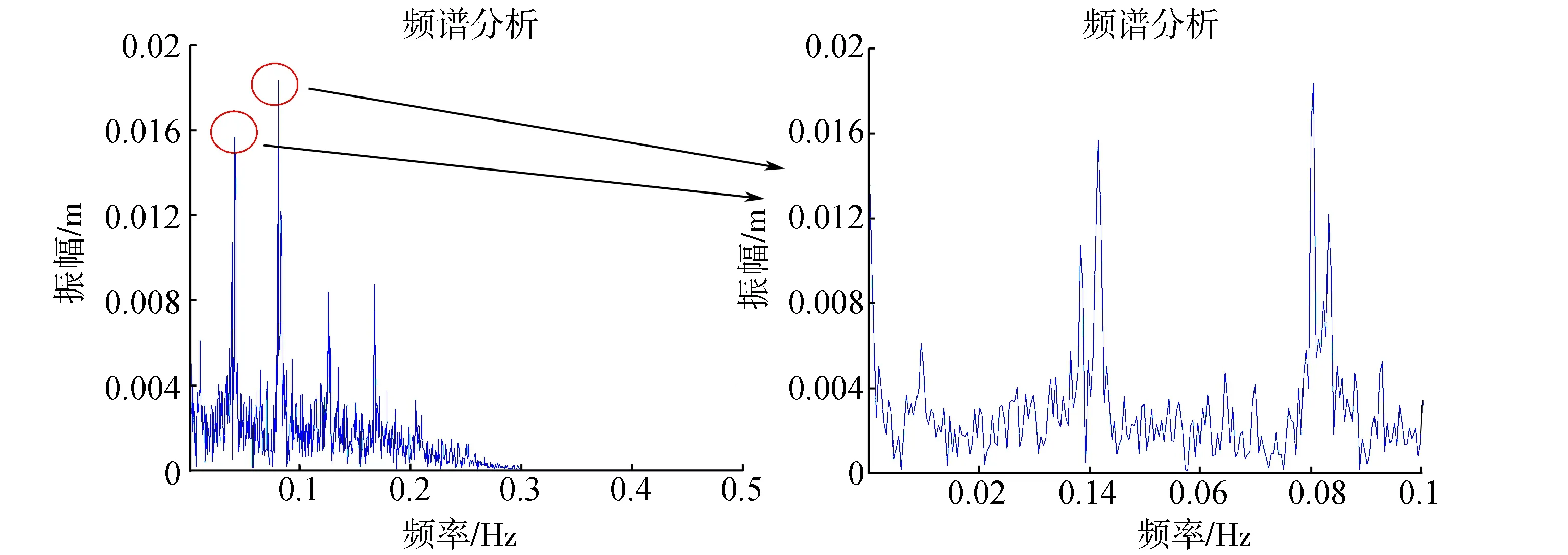
图4 滤波之后频谱结果

为进一步分析小波分析对海潮特征信息的提取的影响，本文将两种方法的海潮特征值与目前比较流行的全球海潮模型FES2004进行比较，模型值特征值通过瑞典Onsala天文台获得。反演值与模型性的振幅差值如图5所示。

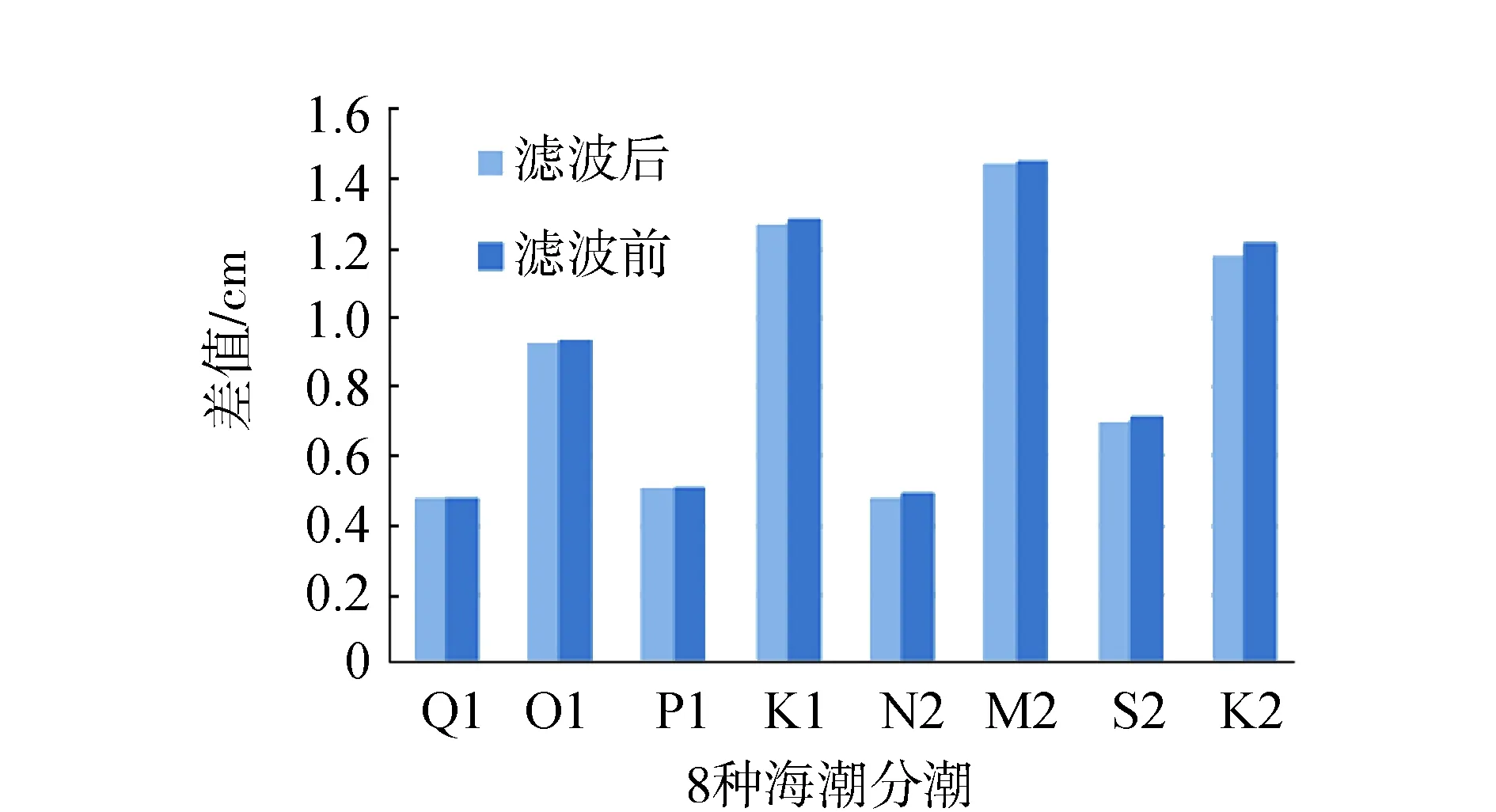
图5 滤波前后与模型值比较结果

从图5可知，经过小波去噪之后，反演值与模型值差值均有不同程度减少，最大方向为K1分潮，达到0.14 mm，说明经小波去噪后，海潮模型的反演精度得到提高；而海潮模型数量级仅为mm～cm，因此相较于海潮模型本身的数值，小波去噪对于海潮特征信息提取精度的改正效果已非常明显。

4 结论与建议

海潮负荷是精密单点定位中不可忽视的一个误差源，目前基于GPS精密坐标时间序列对海潮模型的研究越来越多，但是坐标时间序列不可避免会包含有噪声信号，而时间序列的精度决定最终海潮特征值的提取精度。本文考虑利用小波分析对坐标时间序列进行去噪试验，并将两种方法得到的海潮负荷特征值与FES2004模型值进行比较。实验表明:①小波分析可提高时间序列的精度；②经小波去噪后，海潮特征信息的提取精度有所提高，最多可达0.14 mm，考虑到海潮模型特征值的数量级在mm～cm之间，小波分析已明显提高海潮特征值的提取精度。

本次选择站点较少，时间序列也较短，未来考虑利用站点的分布以及更长GPS时间序列对海潮特征信息进行进一步研究。

[1] 范朋飞.高精度GPS站点坐标时间序列分析与应用[D]. 西安：长安大学，2013.

[2] 袁林果，丁晓利，孙和平，等.利用GPS技术精密测定香港海潮负荷位移[J].中国科学(D辑：地球科学)， 2010 (6): 699-714.

[3] YUAN L G，DING X L，ZHONG P，et al. Estimates of ocean tide loading displacements and its impact on position time series in Hong Kong using a dense continuous GPS network[J].Journal of geodesy，2009， 83(11): 999-101.

[4] THOMAS I D，KING M A，CLARKE P J. A comparison of GPS， VLBI and model estimates of ocean tide loading displacements[J].Journal of Geodesy， 2007， 81(5): 359-368.

[5] ZHAO Q,ZHANG M,ZHANG,et al.，2014.Extraction of Ocean Tide Semidiurnal Constituents’ Vertical Displacement Parameters Based on GPS PPP and Harmonic Analysis Method[C]. China Satellite Navigation Conference (CSNC). Proceedings: Volume II， Lecture Notes in Electrical Engineering 304，DOI: 10.1007/978-3-642-54743-0_28.

[6] 张燕，吴云，施顺英，等.GPS时间序列揭示地震前兆的初步探索[J].大地测量与地球动力学，2005(3):96-99.

[7] 黄声享，刘经南.GPS变形监测系统中消除噪声的一种有效方法[J].测绘学报，2002(2):104-107.

[8] 黄声享，刘经南，柳响林.小波分析在高层建筑动态监测中的应用[J]. 测绘学报，2003(2):153-157.

[9] 许杭,王俊杰,高俊强.小波分析去噪在腰沙围垦变形监测中的应用[J].测绘与空间地理信息，2016,39(3)：189-192.

[10] 张德丰.MATLAB小波分析[M].北京:机械工业出版社,2009.

[11] 陈宗镛.潮汐学[M].北京：科学出版社，1980.

[12] 赵红.海潮负荷影响及其模型精化研究[D]. 西安：长安大学，2013.

[13] 范士杰，刘焱雄，王振杰.日本3· 11特大地震的GPS震时和震后响应[J].武汉大学学报(信息科学版)，2012，37(2):191-194.

[14] 徐晓庆，方国洪，王新怡，等.渤、黄、东海潮汐的相对导纳及N2，K2，P1和Q1分潮的经验同潮图[J].海洋科学进展，2011，29(3):293-306.

[责任编辑：李铭娜]

A study of de-noising of vertical tide characteristic data based on wavelet analysis of the

CHEN Yun1, WU Zhilu1,HE Lina1,2

(1.School of Earth Science and Engineering, Hohai University, Nanjing 211100，China;2.State Key Laboratory of Geo-information Engineering,Xi’an 710054,China)

Currently many scholars at home and abroad use high precision coordinate time series in coastal GPS stations to extract the characteristic information of the tide, which has made many achievements. But high precision coordinate time series contain lots of inevitable noise, which affect the extraction in the characteristic information. In this paper, based on 67 days coordinate time series of the result of precise point positioning (PPP) of the Japanese GPS station (GMSD), wavelet analysis is used to make de-noising experiments. After Fast Fourier Transform (FFT) method, by comparing the extraction with FES2004 tidal model of the eigenvalue.The results show as follows: the wavelet analysis can improve the accuracy of coordinate time series; wavelet analysis can improve the accuracy of eigenvalue, which is up to 0.14 mm. Compared with scale in mm～cm level between eigenvalue of the tide, the accuracy of wavelet analysis in inversion precision is quite required.

wavelet analysis; time series; PPP; tide characteristics; FFT

10.19349/j.cnki.issn1006-7949.2017.03.014

2016-03-07

国家自然科学基金资助项目(41404025)；地理信息工程国家重点实验室开放基金(SKLGIE2014-M-2-2)；中央高校基本科研业务费专项资金资助(2014B03314)；大学生创新训练课题(2015102941143).

陈 运(1995-)，女，本科生.

吴志露(1990-)，男，博士.

P228

A

1006-7949(2017)03-0065-04

引用著录：陈运，吴志露，何丽娜.小波分析在垂向海潮特征信息去噪研究[J].测绘工程，2017，26(3)：65-68.