多层缠绕提升机卷筒绳槽参数研究
2017-12-22刘文强龚宪生宁显国
刘文强,龚宪生,宁显国,万 园
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.重庆大学 机械工程学院,重庆 400044)
多层缠绕提升机卷筒绳槽参数研究
刘文强1,2,龚宪生1,2,宁显国1,2,万 园1,2
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.重庆大学 机械工程学院,重庆 400044)
研究超深矿井多层缠绕提升系统绳槽参数的选取规律。在超深矿井多绳多层缠绕提升过程中,钢丝绳拉力不断地随提升高度变化,卷筒变形和钢丝绳张力相互影响,及钢丝绳层间拉力降低,建立卷筒和钢丝绳拉力相互影响的力学模型,计算钢丝绳变形量,研究绳槽参数变化规律,为超深矿井提升装备卷筒绳槽参数设计和选取提供理论参考。研究结果表明:在缠绕6层时,节距取值范围为1.032 6~1.414 d,绳槽最佳直径为1.032 6 d,接触深度为0.329 d;通过分析节距对圈间过渡加速度的影响,得到不同节距下圈间过渡加速度曲线,结果表明,节距越小对减小圈间过渡加速度越有利。研究方法和结果可为超深矿井提升机绳槽的设计、合适的绳槽参数选取提供参考。
多层缠绕;提升机;绳槽节距;绳槽深度;绳槽直径
随经济的不断发展,我国对于大型矿产资源的需求不断增大,但浅层矿产资源已经消耗殆尽,为了满足经济发展的需求,深层矿产资源的开发已经迫在眉睫。目前,我国矿山的平均开采深度在500 m左右,随浅层矿产资源的消耗,未来10 a内,我国矿井的开采深度必然达到1 000~2 000 m[1]。对于超深矿井提升(井深>1 200 m),由于多绳摩擦式提升机会尾绳过重而导致有效提升载荷降低、钢丝绳应力波动过大而影响钢丝绳寿命,单绳缠绕式提升机受钢丝绳和卷筒尺寸限制,均无法满足超深矿井重载提升的要求。因此,双折线平行绳槽多绳多层缠绕式提升系统有望成为超深井提升装备的有效型式,如图1所示。
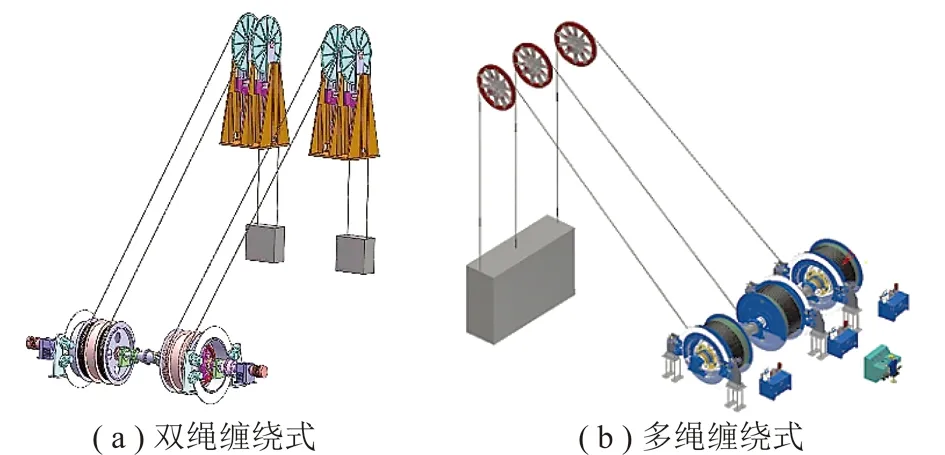
图1 多绳缠绕式提升机示意Fig.1 Diagram of the ultra-deep mine hoist
对于传统单绳缠绕式提升装备已经有完善的设计理论,主要有:钢丝绳拉力降低系数研究[2];层间过渡块设计[3];层间过渡加速度和对挡绳板挤压力研究[4-5];卷筒主轴装置设计[6-8];运行安全设计[9-11]等。与传统单绳缠绕式提升设备相比,多绳缠绕式提升机卷筒分为两个或多个缠绳区,钢丝绳分别在各缠绳区多层缠绕,并分别通过天轮连接到罐笼来实现同步提升。由于高速重载提升,卷筒和钢丝绳变形量大,引起的缠绕误差大,增大了同步提升的难度。因此,选取合理的绳槽参数有利于钢丝绳的平稳缠绕,有利于减小缠绕误差。
本文拟研究绳槽参数的选择依据,为绳槽的设计提供理论基础。多层缠绕卷筒和钢丝绳相互作用关系复杂,当钢丝绳缠绕到卷筒上后钢丝绳的张力引起卷筒变形,卷筒变形反过来引起钢丝绳张力降低,每缠绕上一层钢丝绳也会引起卷筒变形和下层钢丝绳变形,引起下层钢丝绳张力降低,这样导致层间钢丝绳张力降低。这些与绳槽节距也有关。国内外关于卷筒、钢丝绳结构和多层缠绕钢丝绳张力降低的研究较多,杨家驹[12]采用平衡系统法分别研究了1~4层钢丝绳的拉力降低系数。葛世荣[13]建立静不定计算模型,研究筒壳载荷变化规律,与实验结果对比误差较小。刘守成[14]考虑卷筒径向变形和钢丝绳断面变形对张力的削弱,提出多层卷绕径向压力的计算方法,得出钢丝绳直径等于节距时能很好的缠绕;龚伟安[15]在考虑支承条件下通过解析法,给出了均布外压下,筒壳变形与应力的准确解。龚宪生[16]建立钢丝绳多层缠绕与双绳区卷筒在圈间、层间缠绕时的耦合变形模型,得到卷筒在各圈缠绕时的受载情况,WU Juan[17]提出了钢丝绳受拉伸载荷时的有限元模型。目前,关于绳槽参数的研究很少。夏荣海[18]分析了最大内偏角和缠绕间隙的关系。江华[19]从最大许用偏斜角的角度计算了螺旋绳槽相邻绳圈之间的最小间隙。
由于多层缠绕过程中钢丝绳和卷筒相互作用关系比较复杂,而绳槽的设计必然要考虑卷筒及钢丝绳的变形。因此,本文拟考虑钢丝绳层间拉力降低,建立卷筒和钢丝绳拉力降低相互影响的力学模型,计算钢丝绳变形量,考虑钢丝绳的变形后选取合适的绳槽参数,为超深矿井提升装备绳槽参数设计提供理论参考。
1 钢丝绳张力及变形
设卷筒半径为R,厚度为δ,弹性模量为E,绳槽节距为t,钢丝绳对卷筒的压力为P,钢丝绳拉力为T,厚度方向壁上受正压应力为σ,径向变形量为ΔR,微元体dθ上卷筒及钢丝绳受力如图2所示,建立卷筒的受力变形方程:
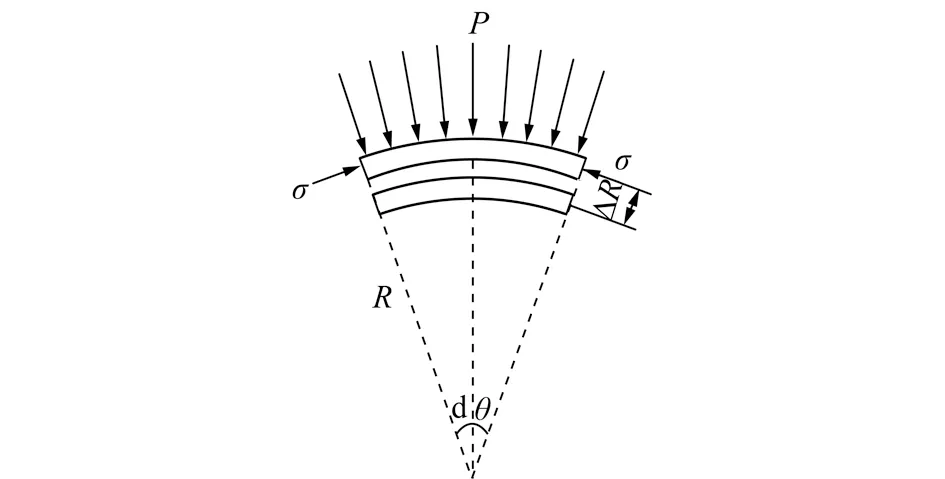
图2 卷筒受力Fig.2 Loads on drum
卷筒上钢丝绳的拉力为T,受力如图3所示,其受力平衡方程为
则
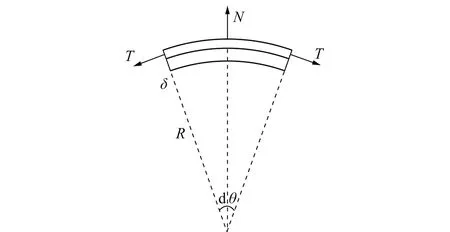
图3 钢丝绳受力Fig.3 Loads on rope
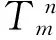
卷筒变形量及受到的压力为


图4 钢丝绳间相互作用力Fig.4 Interacting forces between ropes
则
将F和Fs沿竖直和水平方向分解,得
其中γ=arctanμ。
将两侧竖直和水平方向力叠加,钢丝绳的横向弹性模量为E1,直径为d,变形如图5所示,则钢丝绳在竖直方向的变形方程为

图5 钢丝绳变形Fig.5 Deform of rope
水平方向的变形方程为
此变形是假设力作用在竖直和水平极限点,而真实钢丝绳接触力与水平面呈β角,以接触点竖直方向长度为比例近似表示,钢丝绳横向泊松比v1,得钢丝绳在竖直方向的总变形为
令ΔRn表示第n层缠绕相对上一层造成的卷筒径向变形量,则第1层钢丝绳在第2层缠绕后的相对径向变形量为
钢丝绳拉伸弹性模量为E2,则第1层钢丝绳的拉力降低量为

…
…
对第1层钢丝绳有:
对第m层钢丝绳有:
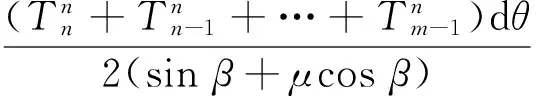

2 绳槽参数
2.1 绳槽最小直径
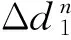
2.2 最小绳槽节距

最小节距为
2.3 最大节距

因此,将绳槽的最大节距取为
2.4 绳槽深度
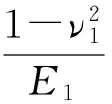
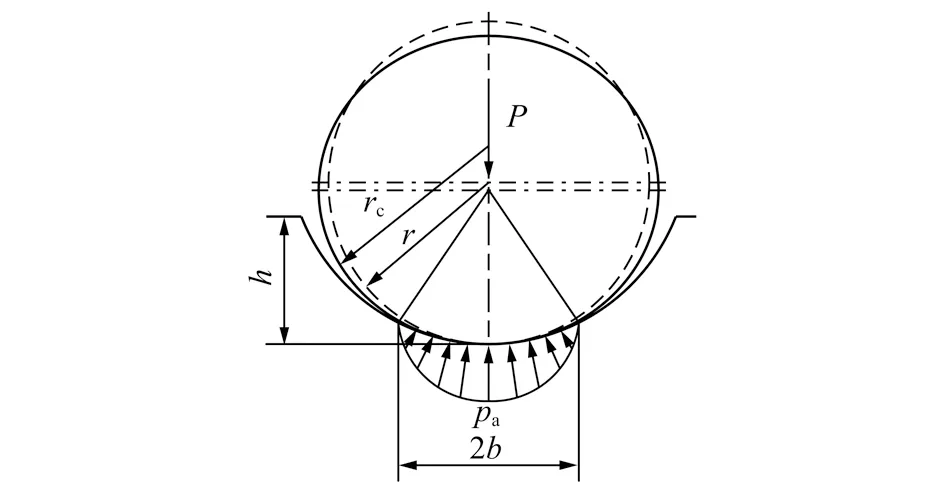
图6 钢丝绳和绳槽接触Fig.6 Contact between rope and groove
通过钢丝绳和绳槽接触的几何关系,得出缠绕至第n层时钢丝绳与绳槽接触的深度为
3 绳槽参数计算及其结果分析
以中信重工超深井试验台提供的参数为依据,见表1。
根据表1中的参数,代入第1节中的数学模型,通过Matlab计算每层缠绕时钢丝绳的变形量和拉力变化情况,再通过几何关系计算缠满n层后,绳槽的最小节距、最小直径、绳槽深度随缠绕层数、节距的变化情况。为了适应未来超深矿井发展趋势,本文拟计算缠绕6层时绳槽的参数取值。根据计算的结果,缠绕n层时最小节距见表2。
表1超深矿井提升系统参数
Table1Parametersofultra-minehoistingsystem
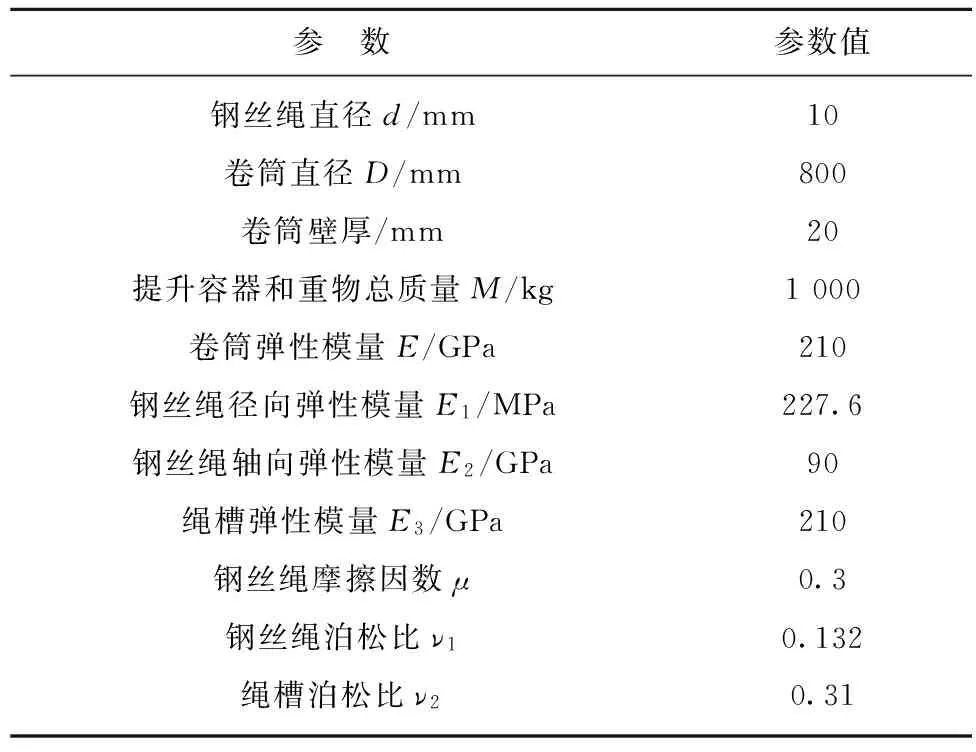
参 数参数值钢丝绳直径d/mm10卷筒直径D/mm800卷筒壁厚/mm20提升容器和重物总质量M/kg1000卷筒弹性模量E/GPa210钢丝绳径向弹性模量E1/MPa227.6钢丝绳轴向弹性模量E2/GPa90绳槽弹性模量E3/GPa210钢丝绳摩擦因数μ0.3钢丝绳泊松比ν10.132绳槽泊松比ν20.31
表2不同层最小节距值
Table2Minimumpitchofdifferentlayers

层数n123456tmin/mm1010.09110.15710.22510.28110.326

图7 不同层最小节距Fig.7 Minimum of pitch of different layers
如图8所示,2~6层最小绳槽直径随节距的增大而减小,因为随节距的增大,钢丝绳变形量将减小,因此其最小直径也随之减小。如图9所示,随缠绕层数的增加,绳槽直径逐渐增大,且节距越小时增大的趋势较节距大时明显,这是由于节距较小时钢丝绳的变形量较大,且节距越小,钢丝绳变形量增大的趋势越明显,说明钢丝绳变形与节距是非线性关系。图10表示节距t=10 mm和t=14.14 mm时各层绳槽直径的变化,可知节距从最小值到最大值范围内变化时,绳槽直径也有明显的变化,且随缠绕层数的增加,绳槽直径的变化范围逐渐增大。
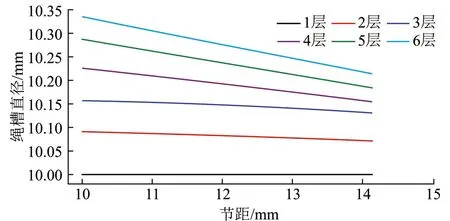
图8 不同节距下各层绳槽直径Fig.8 Diameter of rope groove of different pitches
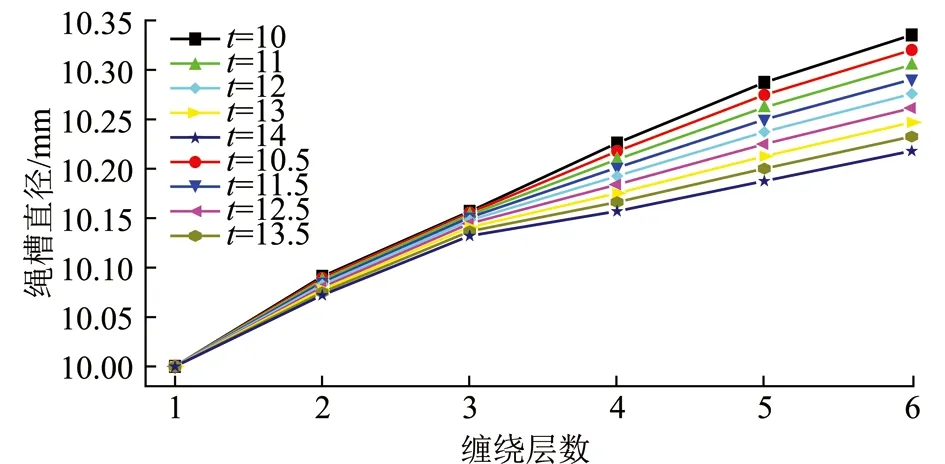
图9 不同层最小绳槽直径Fig.9 Minimum groove diameter of different layers

图10 2~6层绳槽直径取值范围Fig.10 Diameter ranges of rope groove of 2~6 layers
缠满6层时,第1层钢丝绳变形量随节距的变化量不大,约为0.12 mm,因此取绳槽直径为钢丝绳变形量最大时的直径,此时dc为10.326 mm,根据式(52),计算绳槽直径为10.326 mm时,不同节距下第1层钢丝绳与绳槽接触宽度b,如图11所示。

图11 不同节距和层下各层接触宽度Fig.11 Contact width of different pitches and layers
由图11(a)可知,缠绕层数为1~6层时,各层缠绕时钢丝绳与绳槽的接触宽度随节距的增大逐渐减小,因为节距增大钢丝绳变形量减小,与绳槽的接触宽度也随之减小。由图11(b)可知,接触宽度随缠绕层数的增加而增大,但不是线性关系,而是层数越多,增大的越平缓,这是由于层间拉力降低引起的;2~6层缠绕时,不同节距下,接触宽度变化幅值很小,其中第2层时为0.44 mm,第3层缠绕时差值0.45 mm,第4层为0.51 mm,第5层为0.92 mm,第6层为0.98 mm。4~6层时整体增大的比较缓慢,且节距越小增大的幅度略大。

图12 不同节距和层下的接触深度Fig.12 Contact depth of different pitches and layers
通过钢丝绳与绳槽接触的几何关系计算可得,如图12(a)所示,各层接触深度随节距t的增大而减小,随缠绕层数的增加而增大(表3),因为随节距的增大,上层钢丝绳对第1层钢丝绳沿竖直方向的分力将减小,导致钢丝绳变形量减小,从而钢丝绳与绳槽的接触深度也将减小,而随缠绕层数的增加,第1层钢丝绳受上层钢丝绳作用力增大,变形量也增大,因此和绳槽的接触深度也随之增大;图12(b)中,缠绕2层和缠绕3层时接触深度变化不大,因为在缠绕3层以内时,卷筒和钢丝绳变形量较小,节距对变形量的影响不大;当缠绕4层及以上时,节距越小,接触深度相对2~3层增加比较明显,节距越大,接触深度增加的比较平缓,因为随缠绕层数的增加,节距对钢丝绳的变形量的影响逐渐增大,和图8的变化相符合。在选取绳槽参数时,应适当增大绳槽深度,保证绳槽深度略大于钢丝绳与绳槽接触的实际深度,从而预留一定的安全余量。
表3接触深度变化范围
Table3Rangesofcontactdepth

层数n23456接触深度h/mm0.907~1.0701.329~1.5451.744~2.0521.982~2.6782.395~3.294
由图13可知,层间拉力降低系数随节距的增大而减小,因为卷筒和钢丝绳变形量随节距的增大而减小,变形量越大,层间拉力降低量就越大。在缠绕至第6层时,层间拉力不是逐层增加的,而是受节距的影响,t=10~12 mm时,1~3层逐渐减小,第3层达到最低,4~6层逐渐增大,并且第4层拉力大于第1层拉力,因为此时第1~2层钢丝绳和卷筒变形量较大,造成第3层钢丝绳拉力降低比较明显;t>12 mm时,层间拉力在第2层达到最小值,且第3层和第1层拉力接近,此时卷筒和钢丝绳的变形量较小,对第2层拉力有比较明显的降低,而对第3层的影响相对较小。
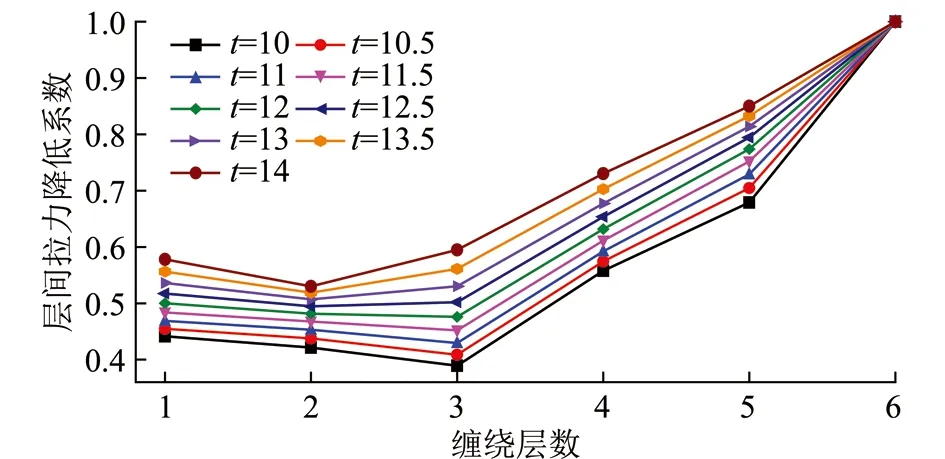
图13 不同节距层间拉力降低Fig.13 Ropes’ tension reduction coefficient of different pitches
4 绳槽间隙对圈间过渡加速度的影响
如图14所示,根据几何关系有:
式中,ε为绳槽间隙。
尼康D500倾向于保留高光细节,在光比较大的场景中,D500的画面会偏暗,相比之下X-H1的拍摄效果更接近目视效果。
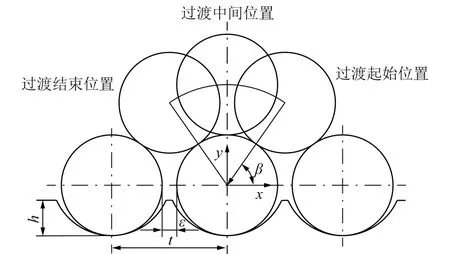
图14 圈间过渡加速度Fig.14 Acceleration of transition between the circles
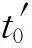
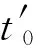
圈间过渡时上层钢丝绳从过渡的起始位置到结束位置沿水平方向的平均速度为

x=vxt

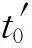

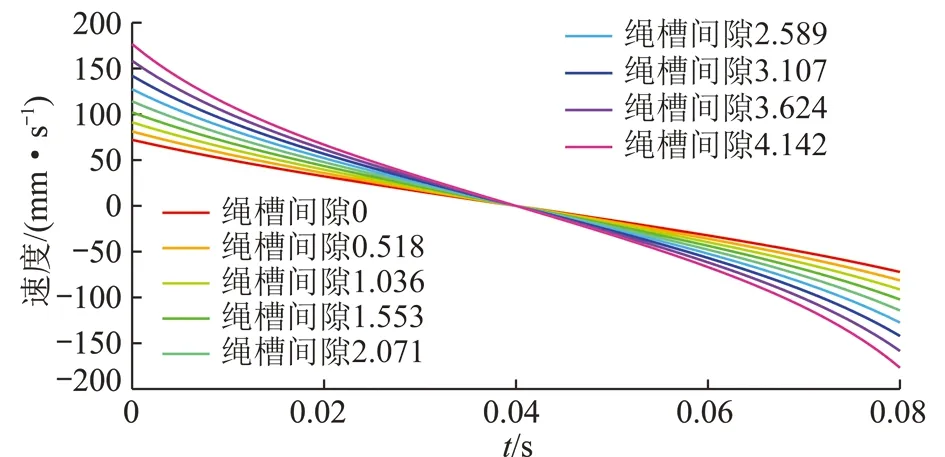
图15 不同间隙下圈间过渡速度变化Fig.15 Variation of speed of different gap of circles
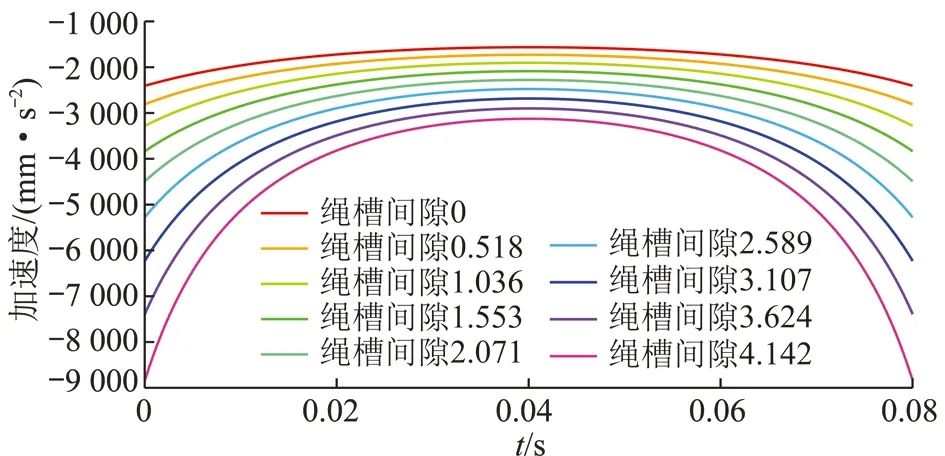
图16 不同间隙下圈间过渡加速度变化Fig.16 Variation of acceleration of different gap of circles
5 结 论
(1)对超深矿井的多层缠绕式提升机建立卷筒和钢丝绳缠绕相互影响的力学模型,计算不同节距时多层缠绕钢丝绳的变形量,通过变形后的钢丝绳取绳槽最小节距和最小直径,再计算接触的深度,得到了绳槽节距、直径、深度变化曲线。工程实践中可以根据需要按照图中变化曲线参考选取合适的值。对试验提升机,研究结果表明,缠绕6层时,节距取值范围为1.032 6~1.414 d,绳槽最佳直径为1.032 6 d,绳槽深度应略大于钢丝绳与绳槽的接触深度0.329 d。
(2)从圈间过渡加速度的角度分析节距对加速度的影响。结果表明,节距越小对减小圈间过渡加速度越有利,选取节距参数时,宜选取多层缠绕排绳稳定后保证同层相邻绳圈不发生挤压的前提下的最小节距。
(3)研究得到绳槽参数的设计选择方法对单绳、多绳多层缠绕均适用,对于别的系统,只需把相应的参数代入理论模型中计算相应的参数,从而得出合理的绳槽参数。
(4)研究中未将提升过程中钢丝绳垂绳质量变化考虑在内,对钢丝绳的径向变形计算没有考虑股与股、丝与丝之间的相互影响,故对计算结果会造成微量的偏差。
以上研究提出的方法和所得结果可为超深矿井提升机绳槽的设计、合适的绳槽参数选取提供参考。
[1] 刘劲军,邹声勇,张步斌,等.我国大型千米深井提升机械的发展趋势[J].矿山机械,2012,40(7):1-5.
LIU Jinjun,ZOU Shengyong,ZHANG Bubin,et al.Discussion trend of domestic large hoisting equipment for deep shafts of thousands meters[J].Mining & Processing Equipment,2012,40(7):1-5.
[2] 张义儒.钢丝绳拉力降低系数的计算[J].河南理工大学学报(自然科学版),1985(2):70-76.
[3] 龚宪生,杨雪华,夏荣海.提升机钢丝绳多层缠绕平稳过渡的研究[J].煤炭学报,2000,25(2):212-216.
GONG Xiansheng,YANG Xuehua,XIA Ronghai.Study on stable coiling of multiple layers of wire rope on cylindrical drum hoists[J].Journal of China Coal Society,2000,25(2):212-216.
[4] 杨厚华.层间过渡时提升钢绳的压力计算[J].贵州工业大学学报:自然科学版,2000,29(2):31-35.
YANG Houhua.Pressure calculation in winding rope during layer-to-layer transition[J].Journal of Guizhou University of Technology:Natural Science Edition,2000,29(2):31-35.
[5] 杨厚华.层间过渡时钢绳对滚筒轮缘的挤压力[J].现代机械,2000(1):73-75.
[6] JIN Minjie,WAN Hanbing,CHEN Hongzhang,et al.The optimum design of main shaft device of double reels for wrapped hoist[J].International Journal of Information and Systems Sciences,2005,1(3-4):398-405.
[7] 龚宪生,曹静,陈器,等.提升机主轴装置结构应力应变场数值模拟及优化分析方法[J].中国机械工程,2009,20(21):2575-2580.
GONG Xiansheng,CAO Jing,CHEN Qi,et al.Structure optimization and numerical simulation of stress and strain fields for the main shaft device of a hoist[J].China Mechanical Engineering,2009,20(21):2575-2580.
[8] 李自贵,解龙翔.基于MATLAB的单绳缠绕式提升机主轴振动特性研究[J].矿山机械,2013,41(11):61-65.
LI Zigui,XIE Longxiang.Study on vibration characteristics of spindle of single-rope winding hoist based on MATLAB[J].Mining & Processing Equipment,2013,41(11):61-65.
[9] 龚宪生,谢志江,杨雪华.矿井提升机多层缠绕钢丝绳振动控制[J].振动工程学报,1999,12(4):460-467.
GONG Xiansheng,XIE Zhijiang,YANG Xuehua.Vibration control on winding wire rope of multiple layers on mine hoists[J].Journal of Vibration Engineering,1999,12(4):460-467.
[10] 刘小平,徐桂云,任世锦,等.基于HHT-DDKICA和支持矢量数据描述方法的提升机故障监测[J].机械工程学报,2012,48(23):65-75.
LIU Xiaoping,XU Guiyun,REN Shijin,et al.Hoist machinery fault monitoring based on HHT-DDKICA and support vector data description method[J].Journal of Mechanical Engineering,2012,48(23):65-75.
[11] 李娟莉,杨兆建.基于本体的矿井提升机故障诊断方法[J].振动、测试与诊断,2013,33(6):993-1094.
LI Juanli,YANG Zhaojian.Fault diagnosis method for mine hoist based on ontology[J].Journal of Vibration,Measurement & Diagnosis,2013,33(6):993-1094.
[12] 杨家驹.钢丝绳多层缠绕拉力降低系数——缠绕系数[J].辽宁工程技术大学学报,1982(2):49-56.
YANG Jiaju.Drop coefficient of pulling force for the multiple coat steel cable twined on the drum[J].Journal of Liaoning Technical University,1982(2):49-56.
[13] 葛世荣,孙玉荣.多层缠绕卷筒壳载荷计算的静不定方法[J].中国矿业学院学报,1987(2):39-48.
GE Shirong,SUN Yurong.Statically indeterminate method for calculating the load produced by multilayer ropes upon the hoisting drum[J].Journal of China University of Mining & Technology,1987(2):39-48.
[14] 刘守成,依·彼·克摇其科夫.起重机多层卷绕卷筒径向压力的研究[J].大连工学院学刊,1962(3):25-47.
[15] 龚伟安.缠绕筒壳的弹性理论及应力计算问题[J].矿山机械,1976(4):13-42.
GONG Weian.Elastic theory and stress calculation of drum[J].Mining & Processing Equipment,1976(4):13-42.
[16] 龚宪生,罗宇驰,吴水源.提升机卷筒结构对多层缠绕双钢丝绳变形失谐的影响[J].煤炭学报,2016,41(8):2121-2129.
GONG Xiansheng,LUO Yuchi,WU Shuiyuan.Effect of drum structure of mine hoist on multilayer winding and multipoint lifting ropes’ discordance[J].Journal of China Coal Society,2016,41(8):2121-2129.
[17] WU Juan.The finite element modeling of spiral ropes[J].International Journal of Coal Science & Technology,2014,1(3):346-355.
[18] 夏荣海.矿井提升设备容许最大绳弦内偏角和钢丝绳缠绕间隙[J].煤炭学报,1964(2):3-12.
XIA Ronghai.The maximum allowable inner fleet angle and clearance between wound-on coils for mine hoists[J].Journal of China Coal Society,1964(2):3-12.
[19] 江华.卷筒绕进绕出钢丝绳与相邻绳的最小间距计算[J].起重运输机械,2011(S1):24-25.
[20] 陈国荣.弹性力学[M].南京:河海大学出版社,2001:132-136.
Researchonropegrooveparametersofmultilayerwindinghoistdrum
LIU Wenqiang1,2,GONG Xiansheng1,2,NING Xianguo1,2,WAN Yuan1,2
(1.TheStateKeyLaboratoryofMechanicalTransmission,ChongqingUniversity,Chongqing400044,China; 2.CollegeofMechanicalEngineering,ChongqingUniversity,Chongqing400044,China)
This paper studies the selection rule of rope groove parameters for the multi-layer winding hoisting system of ultra-deep mine.In the process of multi-rope and multi-layer winding lifting,the tension of the wire rope is constantly changing with the lifting height and the deformation of the drum and the tension of the wire rope affects each other.In considering the decrease of rope’s tension in layers,the mechanical model of the mutual influence of drum and wire rope is established to calculate the deformation of wire rope and to study the variation of rope parameters,which provide theoretical reference for the design and selection of the parameters of the rope groove of drum.The results show that the pitch ranges from 1.032 6 d to 1.414 d,the best diameter of the groove is 1.032 6 d and the contact depth is 0.329 d.By analyzing the effect of pitch on the inter-circle transition acceleration,the transition curve of inter-circle transition is obtained.The results show that the smaller the pitch is,the more favorable the acceleration is.The research methods and results can effectively guide the design of the rope groove of ultra-deep mine hoist and the selection of appropriate rope groove parameters.
multilayer winding;hoist;pitch of groove;depth of groove;groove diameter
刘文强,龚宪生,宁显国,等.多层缠绕提升机卷筒绳槽参数研究[J].煤炭学报,2017,42(11):3035-3043.
10.13225/j.cnki.jccs.2017.0321
LIU Wenqiang,GONG Xiansheng,NING Xianguo,et al.Research on rope groove parameters of multilayer winding hoist drum[J].Journal of China Coal Society,2017,42(11):3035-3043.doi:10.13225/j.cnki.jccs.2017.0321
TD534
A
0253-9993(2017)11-3035-09
2017-03-13
2017-08-16责任编辑许书阁
国家重点基础研究发展计划(973)资助项目(2014CB049403)
刘文强(1990—),男,重庆人,硕士研究生。E-mail:20140713191@cqu.edu.cn。
龚宪生(1956—),男,重庆人,教授,博士生导师,博士。E-mail:cqxsgong@cqu.edu.cn
