空气间隔装药孔壁初始冲击压力分析
2017-12-22楼晓明王振昌陈必港王作棠
楼晓明,王振昌,陈必港,王作棠,俞 缙
(1.福州大学 紫金矿业学院,福建 福州 350116; 2.福州大学 爆炸技术研究所,福建 福州 350116; 3.中国矿业大学 矿业工程学院,江苏 徐州 221116; 4.华侨大学 岩土工程研究所,福建 厦门 361021)
空气间隔装药孔壁初始冲击压力分析
楼晓明1,2,王振昌1,2,陈必港1,2,王作棠3,俞 缙4
(1.福州大学 紫金矿业学院,福建 福州 350116; 2.福州大学 爆炸技术研究所,福建 福州 350116; 3.中国矿业大学 矿业工程学院,江苏 徐州 221116; 4.华侨大学 岩土工程研究所,福建 厦门 361021)
为分析空气间隔装药时孔壁的初始冲击压力,引入Starfield迭加法,将柱状药包等效为有限个单元球形药包,考虑压力沿炮孔轴向的衰减及叠加作用,分析得到上部空气间隔装药及中部空气间隔装药条件下的孔壁初始冲击压力计算表达式。利用ANSYS/LS-DYNA软件建立数值模型,对监测点进行应力监测;同时,浇筑混凝土模型,并借助高速多路动态应力测试系统测量炮孔周围爆炸应力场,将2种方式的监测结果与理论分析结果相比较。结果显示:上部空气间隔装药,装药段处压力达到最大,随着与装药段距离的增大,压力明显呈先急剧减小、后趋于稳定的趋势;中部空气间隔装药,压力最小值出现在空气柱约1/2处,整体呈两端大、中间小的下凹型分布特征。在2种装药结构下,空气柱中指定点初始冲击压力的理论值与模拟值相对误差均较小。上述结果充分表明:空气间隔装药孔内压力沿炮孔轴向呈不均匀分布,2种装药结构压力分布特征与理论分析结果基本吻合,验证了理论分析的合理性。
空气间隔装药;初始冲击压力;数值模拟;混凝土模型
为改善爆破效果,光面爆破常采用空气间隔装药结构[1-2]。空气间隔装药最关键的一个参数是孔内的空气柱长度,孔壁初始冲击压力与该参数的取值息息相关。显然,孔壁初始冲击压力不同,周围岩体任意点上的动态应力也将不同,最终将影响光面爆破裂缝的贯通效果。因此,开展空气间隔装药孔壁初始冲击压力的研究显得非常重要。
目前,对于空气间隔装药条件下的初始冲击压力,通常按爆生气体准静态压力的8~11倍计算[1-3],具体可表示为式(1)和(2)的形式。此2式是基于爆轰波正入射孔壁且孔壁为刚壁这2个假设条件下的结果,并不考虑应力波沿炮孔轴向的衰减和叠加作用,因此所得孔壁初始冲击压力沿炮孔轴向必然均匀分布,比较适用于分析空气柱较短或连续装药时的情形。而对于空气柱较长时的情形,采用该式进行分析计算显然是不合理的。
当P≥Pk时:
当P 式中,P为气体膨胀压力;Pk为阶段气体临界压力;Pd为初始冲击压力;β为孔壁压力增大倍数,一般取β=8~11;ρe为炸药密度;D为炸药爆轰速度;Kl为轴向不耦合系数,Kl=(la+le)/le,其中la为空气柱长度,le为装药长度;Kd为径向不耦合系数,Kd=db/dc,其中db为炮孔直径,dc为装药直径;k为等熵膨胀指数,一般取k=3。 对于空气柱较长时的孔壁初始冲击压力,国内外学者尝试采用不同的方法,致力于探求更加切合实际的压力分布特征。杨国梁等[4]采用数值计算方法对不同空气间隔装药条件下的孔内压力分布规律进行了系统研究,得出:空气间隔装药孔内各点压力并不相等,装药段中部的孔壁初始冲击压力最大,其值显著大于空气柱段的孔壁初始冲击压力。该结论充分表明了孔壁初始冲击压力沿炮孔轴向呈不均匀分布的特征,但遗憾的是他们未曾用数理表达式对该分布特征加以描述。凌伟明[5]采用锰铜压阻传感器加脉冲恒流源试验系统,对水泥砂浆和有机玻璃介质在耦合与不耦合装药条件下的孔壁初始冲击压力进行了测试,得到了各点的孔壁初始冲击压力值,为直接测量该值提供了参考。倪芝芳等[6]运用锰铜压阻测试系统测量了岩石硝铵炸药、乳化炸药和水胶炸药分别在花岗岩和混凝土中爆炸产生的初始冲击压力峰值,通过回归分析方法得到了孔壁压力与入射角之间的指数型关系,同时指出在炮孔轴向上初始冲击压力与距起爆点的距离有关。该研究成果实测了孔壁初始冲击压力,定量地分析了炮孔轴向上初始冲击压力的分布特征,对空气间隔装药孔壁初始冲击压力有了新的认识。但是,倪等仅考虑了单段装药时的孔壁压力分布,并未考虑双段或多段时的情形,因此仍有待进一步完善。 基于上述分析,本文针对空气柱较长时的孔壁初始冲击压力,引入Starfield迭加法,考虑压力沿炮孔轴向的衰减及叠加作用,分析上部空气间隔装药及中部空气间隔装药2种条件下的孔壁初始冲击压力。 为获得空气柱较长时的孔壁初始冲击压力,引入Starfield迭加法,其基本思想是把柱状药包等效为有限多个具有相同等效半径的单元球形药包的迭加[7],如图1所示。 图1 Starfield迭加法等效单元Fig.1 Equivalent unit of Starfield superposition method 假设单元球形药包的等效半径为re,柱状药包直径为dc。根据药量相等原则,有 再假设柱状药包长度为le,则等效单元球形药包个数可表示为 且最后一个等效药包半径为 利用Starfield迭加法精确地计算出迭加过程中的应力峰值点是一个复杂的过程。各单元球形药包无论是同时起爆或顺序起爆,考虑到柱状药包爆轰特点和应力波在岩石中传播的情况,都将与空气间隔段距离最近的等效单元球状药包爆破时产生的爆炸应力波传播到空气间隔段指定点时的应力值,近似作为该点的应力峰值与实际相差不大,可满足计算要求[7]。值得注意的是,由于炸药爆轰速度与岩石纵波波速处于同一个数量级,故在利用Starfield迭加法计算柱状药包的作用过程中,必须考虑各个等效单元球状药包在迭加过程中的时间效应。对此,已有学者给出了描述单元球药包激发的应力波随时间衰减的指数函数[8]: 式中,A为等效单元球状药包爆破荷载衰减系数,A=Cp(1-2μ)/[a(1-μ)k][9-10];Cp为岩石纵波速度;a为与岩石性质有关的常数。 对于空气间隔段某一指定点,每个等效单元球状药包在整个正压作用时间内对该点都有应力作用。为不失一般性,假设应力峰值总是在某个单元药状包激发的应力波正好传播到该指定点时出现,例如当第k个单元球状药包应力波到达该点时,应力达到最大值,此时第i个单元球状药包在该点的应力已经衰减,其衰减时间为 式中,li为第i个等效单元球形药包到空气柱指定点的距离;lk为第k个等效单元球形药包到空气柱指定点的距离;D为炸药爆速。 同时,根据激波理论,在单个球形药包爆炸作用下,任意点冲击波峰值压力随距离的衰减关系[11]可表示为 对特定的炸药及围岩,其对应的ρ,Ws,B,α为常数,令K=0.98α(ρWs/WT)α/3B,同时为区别于冲击波在岩体中的衰减系数,用δ表示压力沿炮孔轴向的衰减系数,故有 考虑单元球状药包的应力衰减,可得到单个等效单元球形药包在指定点的峰值应力表达式: 在忽略相邻单元球形药包爆炸相互作用的前提下,整个柱状装药段在某点的峰值压力可近似看成所有球形药包在该点峰值应力的迭加。 假设在上部空气间隔装药结构中,空气柱长度为la,孔底装药段长度为le,装药直径为dc,如图2所示。 图2 上部空气间隔装药孔壁初始冲击压力分析Fig.2 Analysis of initial shock pressure for hole wall with up-air-decked charge 因此,整段柱状药包在该点产生的冲击压力可表示为n个单元球形药包在该点的应力叠加,即 假设在中部空气间隔装药结构中,空气柱长度为la,上、下两个装药段分别为I,II装药段,I装药段长度为l1,II装药段长度为l2(l1+l2=le,le为装药段总长度),如图3所示。 图3 中部空气间隔装药孔壁初始冲击压力分析Fig.3 Analysis of initial shock pressure for hole wall with middle-air-decked charge 同理,II装药段传爆到第j个单元球形药包(从装药段顶部到底部,j依次递减,同时满足j≤n2且j为正整数,n2为II装药段划分的等效单元球形药包总个数)时,该球形药包在A′点的冲击压力表示为 因此,上、下2个装药段在该点产生的冲击压力可表示为所有单元球形药包在该点的应力叠加,即 分析式(13)和(16)的函数特征易知,对于上部空气间隔装药结构,沿炮孔轴向方向,冲击压力在装药段处达到最大值,随着与装药段距离的增大,压力不断减小,且在孔口达到最小值;对于中部空气间隔装药结构,沿炮孔轴向方向,冲击压力在上、下两个装药段达到最大值,随着与装药段距离的增大,压力不断减小,且在空气柱1/2处达到最小值,整体呈下凹型分布特征。根据上述分析,可大致绘出孔壁初始冲击压力沿炮孔轴向的变化趋势曲线,如图4,5所示。 图4 上部空气间隔装药结构孔壁初始冲击压力变化趋势Fig.4 Variation trend of initial shock impact pressure for hole wall with up-air-decked charge structure 图5 中部空气间隔装药结构孔壁初始冲击压力变化趋势Fig.5 Variation trend of initial shock impact pressure for hole wall with middle-air-decked charge structure 测试基于电阻应变原理。当试件受到动态应力作用时,粘贴在测点上的应变片会随着试件的变形产生相应的应变,从而引起电阻的变化。将电阻变化转化为电压或电流的变化,再用显示仪器记录电压或电流的变化过程,就能反算出试件发生的应变,计算方法为 式中,ε为试件发生的应变,10-6;U为输出电压,V;k为仪器的灵敏度系数;U0为仪器桥压,V;n为有用桥臂数(仅指测量应变片的数量,不包括补偿片);G为仪器增益。 在式(14)的基础上,结合胡克定律(Hooke’s law):P=εE,即可得到各点所受的应力大小,其中,P为应力值,MPa。 模型测试实验采用成都泰测科技有限公司生产的Blast-Ultra多通道冲击测试仪和扬州科动电子有限责任公司生产的KD60009A型应变放大器作为数据采集设备。将应变片粘贴于预制的应变砖上,将其预埋于混凝土模型中作为接收爆炸信号的传感器。测试系统及其流程图如图6所示。 图6 应力监测测试系统及流程Fig.6 Test system for stress monitoring 混凝土模型尺寸为40 cm(长)×20 cm(宽)×50 cm(高),采用42.5号普通硅酸盐水泥及筛选后的细砂(粒径不大于1 mm)浇注而成,配合比为水泥∶沙子∶水=1∶1∶0.5,室温养护28 d。模型中,采用外径为12 mm的玻璃纤维管预留炮孔,炮孔深度为40 cm,最小抵抗线为5.5 cm,距模型前、后边界各10 cm。采用上部空气间隔装药结构时,在炮孔底部装1枚2号岩石导爆管雷管,上部预留约28 cm空气柱,对应的轴向不耦合系数为Kl=5.0;采用中部空气间隔装药结构时,在炮孔底部和孔口位置各装1枚2号岩石导爆管雷管,中部预留约21 cm空气柱,对应的轴向不耦合系数为Kl=2.5。2种装药结构孔口均用快硬水泥堵塞5 cm,如图7所示。 图7 模型及测点布置Fig.7 Layout of model and measuring point 应变砖制作成长条形,尺寸为3 cm(长)×3 cm(宽)×40 cm(高)。为使爆炸瞬时信号传至应变砖时不产生反射,应保证应变砖和实验模型的波阻抗严格一致,故对两者采用相同的材料配合比[12-13]。为有效测得爆炸应力,应变砖布置在距炮孔约2 cm处,且与之平行。两块应变砖分别布置8个和11个测点,如图7所示。每个测点垂直粘贴2片测试应变片,采用半桥接法,应变片为扬州科动电子有限责任公司生产的BX120-4AA电阻应变计,阻值为120 Ω,灵敏度系数为(2.08±1)%。粘贴应变片时,先用零号砂纸沿与应变砖轴向成45°的方向对试件表面进行磨光,保证其表面光滑、无镶嵌砂砾等,再用502胶水进行粘贴,待胶水发粘时迅速将应变片按正确位置粘贴,并挤出多余胶水,确保应变片与应变砖良好接触。 在实验模型的制作过程中,同时制作了3组5 cm(长)×5 cm(宽)×10 cm(高)的标准试件,与实验模型在相同的环境中养护28 d后进行相关的力学参数测定,测定结果见表1。 表1实验模型物理力学参数 试块编号密度/(kg·m-3)纵波波速/(m·s-1)弹性模量/GPa抗压强度/MPa12247.12311526.442022153.24306725.853032177.00313924.5020平均值2192.45310025.5023.33 仪器参数设置如下:采样速率为4 MSps;采集时长为10 ms;负延时为1 ms;触发电平为5%;增益为100;桥压为2 V;低通为1 kHz。按照上述测试方案,得到上部空气间隔装药结构与中部间隔装药结构爆炸应力分布数据各一组,见表2,图8为测试典型波形图。 表2上部空气间隔装药结构与中部间隔装药结构应力测试结果 装药结构测点编号与孔底距离/m与孔底相对距离峰值电压/V峰值应变峰值压力/MPa1002.89514092359.34620.0352.923.10615118385.50530.0705.832.83614180361.590单孔单段连续40.1058.752.10610530268.515上部空气间隔装药50.17514.581.0425210132.85560.24520.410.332166042.33070.31526.250.19597524.86380.38532.080.16281020.6551003.34516725426.48820.0352.923.50417521446.77830.0705.833.25816290415.39540.1058.752.42112105308.67850.14011.671.2736365162.308双段装药60.17514.581.1885940151.470中部空气间隔装药70.21017.501.1935965152.10880.24520.422.28511425291.33890.28023.333.15015748401.573100.31526.253.51217559447.753110.35029.173.27616377417.608 注:与孔底相对距离=与孔底距离/炮孔直径。 图8 压力测试典型波形Fig.8 Typical waveform of pressure test 2.4.1上部空气间隔装药结构应力测试结果分析 图9为上部空气间隔装药结构压力测试结果。由图9可知,采用上部空气间隔装药时,沿炮孔轴向方向,孔壁初始冲击压力分布情况与图4的形式基本相同。 图9 上部空气间隔装药孔壁应力随孔底相对距离变化拟合曲线Fig.9 Initial pressure for hole wall of up-air-deck changes with the relative distance of hole bottom 2.4.2中部空气间隔装药结构应力测试结果分析 图10为中部空气间隔装药结构压力测试结果。由图10可知,采用中部空气间隔装药时,沿炮孔轴向方向,孔壁初始冲击压力分布情况与图5的形式基本相同。 图10 中部空气间隔装药孔壁应力随孔底相对距离变化拟合曲线Fig.10 Initial pressure for hole wall of middle-air-deck changes with the relative distance of hole bottom 2.4.3讨 论 通过2种不同装药结构的混凝土爆炸模型试验,对应力测试结果进行整理和分析,可以得出: (1)对于上部空气间隔装药结构,其应力峰值呈现在装药段处应力最大,在孔口处应力最小的分布特征;对于中部空气间隔装药结构,其应力峰值呈开口向上的抛物线型分布特征,在装药段处应力最大,在空气柱约1/2处应力最小; (2)无论是上部空气间隔装药结构还是中部空气间隔装药结构,越靠近装药段,应力值越大,最大应力值约为450 MPa。随着与装药段距离的增大,应力值逐渐减小,且初始阶段下降速度较快,后阶段下降速度变缓,最终趋向于稳定; (3)单独观察中部空气间隔装药结构两个装药段的爆炸应力情况,可以发现,其分布特征与上部空气间隔装药的分布特征相同;若同时考虑中部空气间隔装药结构两个装药段的爆炸应力分布情况,可对上、下两个装药段产生的爆炸应力进行简单叠加。 图11 数值模型示意Fig.11 Diagram of numerical simulation model 3.1.1数值模型和参数设置 利用ANSYS/LS-DYNA大型动力有限元分析软件,建立了含1个炮孔的数值模型,其几何尺寸、炮孔规格、炮孔布置均与混凝土试验模型一致,如图11所示。对于上部空气间隔装药结构,分别建立Kl=2.5,3.5,4.0,5.0四种轴向不耦合系数的装药结构模型,其中Kl=5.0对应混凝土模型实验的装药结构;对于中部空气间隔装药结构,分别建立Kl=2.5,3.5,4.0,5.0四种轴向不耦合系数的装药结构模型,其中Kl=2.5对应混凝土模型实验的装药结构。所有模型对应的装药参数,见表3,对于上部空气间隔装药结构,装药总长度即为下部装药段长度,对于中部空气间隔装药结构,装药总长度为上部和下部装药段长度之和。为了观察孔壁初始冲击压力,由孔底向孔口沿炮孔轴线方向选取孔壁上的一列单元作为应力监测点。 表3不同装药条件模型参数设置 轴向不耦合系数炮孔长度/cm堵塞长度/cm空气柱长度/cm装药长度/cm总长度上部长度下部长度2.540521.0014.004.79.303.540525.0010.003.36.704.040526.258.752.95.855.040528.007.002.34.70 为确保数值模拟结果的准确性,建模过程中,岩石材料、炸药材料、空气间隔层材料和炮泥材料分别采用*MAT-PLASTIC-KINEMATIC、*MAT-HIGH-EXPLOSIVEBURN、*MAT-NULL和*MAT-SOIL-AND-FOAM模型描述,同时,炸药和空气的状态方程分别采用*EOS-JWL和*EOS-LINEAR-POLYNOMAIAL描述,各材料模型及其状态方程对应的参数取值,见表4~7。边界条件设置为:模型的左面和顶面设置为自由面,其余平面均设置为无反射边界(Non-reflecting boundary)。计算过程中,炸药材料和空气间隔层材料采用ALE算法,岩石材料采用Lagrange算法。 3.1.2结果分析 上部空气间隔装药和中部空气间隔装药2种装药结构,在不同的装药条件(不耦合装药系数)下,孔壁初始冲击压力峰值沿炮孔轴向的分布特征曲线分别如图12,13所示。 由图12可以看出,对于上部空气间隔装药结构,装药段的压力显著大于空气柱段的压力,且在起爆点附近压力达到最大值,随着与装药段距离的增大,压力值明显呈先急剧减小、后大致趋于稳定的趋势;由图13可以看出,对于中部空气间隔装药结构,上、下装药段的压力显著大于空气柱段的压力,压力同样在起爆点附近达到最大值,越靠近空气柱段中部,压力越小,其最小值出现在空气柱约1/2处,且从整体上来看,该装药结构孔壁压力呈两端大、中间小的下凹型分布特征。对于这2种装药结构,在不同装药条件下所得压力分布曲线具有相似性。上述数值模拟的结果,尤其是上部空气间隔装药Kl=5.0对于的曲线和中部空气间隔装药Kl=2.5对应的曲线与理论分析结论和模型实验结论能较好地吻合,在一定程度上验证了理论分析和模型实验结论的合理性。 表4岩石材料参数 密度/(kg·m-3)弹性模量/GPa泊松比屈服应力/MPa切线模量/GPa硬化系数219225.20.1850.02.01.0 表5炸药材料及状态方程参数 密度/(kg·m-3)爆速/(m·s-1)爆轰压力/GPaA/GPaB/GPaR1R2ωE0/GPaV0181028003.555.4090.0934.51.10.350.0801.0 注:A,B,R1,R2,ω均为材料参数,其中,R1和R2为无量纲参数,ω为格林爱森常数,表示定容条件下压力相对于内能的变化率;E0为单位体积的初始内部能量;V0为相对体积。下同。 表6空气材料及状态方程参数 密度/(kg·m-3)C0C1C2C3C4C5C6E0/GPaV01.29×10-200000.40.4001.0 注:C0~C6为空气材料状态方程的多项式系数。 表7炮泥材料参数 密度/(kg·m-3)剪切模量/GPa体积模量/GPaA0A1A2PCEPS1EPS218001.60×10-21.3280.00331.31×10-70.1232000.05EPS3EPS4EPS5EPS6EPS7EPS8EPS9EPS10P1/GPa0.090.110.150.190.210.2210.250.300P2/GPaP3/GPaP4/GPaP5/GPaP6/GPaP7/GPaP8/GPaP9/GPaP10/GPa3.424.536.7612.7020.8027.1039.2056.60123.0 注:A0,A1,A2为屈服函数常数;PC为拉伸破坏截断压力;EPS1~EPS10为特征体应变;P1~P10为与特征体应变对应的压力。 图12 上部空气间隔装药孔壁初始冲击压力Fig.12 Initial pressure for hole wall with up-air-decked charge 图13 中部空气间隔装药孔壁初始冲击压力Fig.13 Initial pressure for hole wall with middle-air-decked charge 3.2.1数值模型和参数设置 为检验基于Starfield迭加法推导的上部空气间隔装药和中部空气间隔装药2种情况下,炸药爆炸在空气柱部分的初始冲击压力理论公式的合理性,各建立5个数值模型,分别模拟2种装药条件下,柱状药包长度le取1~5倍等效球药包直径(中部空气间隔装药时,上下装药段药包长度均取1~5倍等效球药包直径)的5种情况,模型的几何尺寸如图14所示。其中,柱状药包直径为1.2 cm,根据式(3)可得,等效球药包直径为1.46 cm。设置预留空气柱长度为5 cm,炮孔最小抵抗线为5.5 cm。上部空气间隔装药的炮孔规格为:φ1.2 cm×((1~5)×1.46)cm(药柱长度)+5 cm(空气柱长度);中部空气间隔装药的炮孔规格为:φ1.2 cm×(2×((1~5)×1.46))cm(药柱长度)+5 cm(空气柱长度)。装药段每间隔1.46 cm设置一个起爆点,各起爆点同时起爆。岩石、炸药和空气柱的材料模型及对应的状态方程与孔壁初始冲击压力轴向分布特征验证模型一致,参数设置分别见表4~6。 图14 数值模型示意Fig.14 Diagram of numerical simulation model 3.2.2结果分析 选取空气柱1/2截面远离自由面一侧与孔壁接触的单元为孔壁初始冲击压力监测点。根据模拟结果,可分别获取上部空气间隔装药和中部空气间隔装药2种条件下数值模型中监测点的两组初始冲击压力值。同时,由理论分析结论及几何关系计算可得,该指定计算点的爆炸应力理论值。图15所示为2种装药条件下指定点初始冲击压力理论计算值与模拟值的对比情况。根据理论计算和数值模拟结果可知,在2种装药条件下,数值模拟所得压力值与式(13)和(16)计算压力值的相对误差平均值分别为8.82%和8.96%,均保持在10%以内,可见二者相互印证效果较好,由此说明基于Starfield迭加法推导的上部空气间隔装药和中部空气间隔装药2种情况下,炸药爆炸在空气柱部分的初始冲击压力理论公式是合理可行的。 图15 监测点初始冲击压力随药柱长度变化趋势Fig.15 Variation trend of initial shock pressure with the length of the column at designated point 同时,根据图15所示指定点初始冲击压力随药柱长度的变化趋势可知,空气柱中指定点受到的初始冲击压力理论值和模拟值均呈现随药柱长度的增加而增大的趋势,这与经典爆破理论的观点是相符的。 (1)基于Starfield迭加法,推导得到上部空气间隔装药及中部空气间隔装药2种条件下的孔壁初始冲击压力计算表达式。 (2)应力监测结果及数值模拟结果均表明,空气柱较长时,孔壁初始冲击压力呈不均匀分布。采用上部空气间隔装药时,装药段初始冲击压力最大,随着与装药段距离的增加,压力值明显呈先急剧减小后趋于稳定的趋势,压力最小值出现在孔口处;采用中部空气间隔装药时,装药段初始冲击压力最大,压力最小值出现在空气柱约1/2处,整体呈两端大、中间小的下凹型分布特征。 (3)空气柱中指定点的孔壁初始冲击压力理论值与模拟值的相对误差始终保持在10%以内,基于Starfield迭加法推导的上部空气间隔装药和中部空气间隔装药2种情况下,炸药爆炸在空气柱部分的初始冲击压力理论公式合理可行。 (4)对空气间隔装药孔壁初始冲击压力进行分析,得到了更加切合实际的孔壁压力分布特征,为今后空气间隔装药关键参数-空气柱长度的计算研究提供了良好的理论基础和试验依据。 [1] 徐颖,宗琦.光面爆破软垫层装药结构参数理论分析[J].煤炭学报,2000,25(6):610-613. XU Ying,ZONG Qi.Theoretical analysis on the parameters of smooth blasting soft mat layer charging construction[J].Journal of China Coal Society,2000,25(6):610-613. [2] 郭义奎,张登龙.软岩中巷道掘进光面爆破参数的计算分析[J].矿山压力与顶板管理,2003,20(1):102-103. GUO Yikui,ZHANG Denglong.The calculation and analysis on the parameters of smooth-surface blasting in the course of drifting in soft rock[J].Ground Pressure and Strata Control,2003,20(1):102-103. [3] 陈俊桦,张家生,李新平.基于岩石爆破损伤理论的预裂爆破参数研究及应用[J].岩土力学,2016,37(5):1441-1450. CHEN Junhua,ZHANG Jiasheng,LI Xinping.Study of presplitting blasting parameters and its application based on rock blasting-induced damage theory[J].Rock and Soil Mechanics,2016,37(5):1441-1450. [4] 杨国梁,杨仁树,姜琳琳.轴向间隔装药爆破沿炮孔的压力分布[J].爆炸与冲击,2012,32(6):653-657. YANG Guoliang,YANG Renshu,JIANG Linlin.Pressure distribution along borehole with axial air-deck charge blasting[J].Explosion and Shock Waves,2012,32(6):653-657. [5] 凌伟明.岩石爆破炮孔孔壁压力的试验研究[J].矿冶,2004,13(4):13-16. LING Weiming.Experimental research on explosion pressure on the wall of a borehole in rock[J].Mining and Metallurgy,2004,13(4):13-16. [6] 倪芝芳,李玉民.岩石爆破孔壁初始冲击波压力的理论计算与拟合[J].岩石力学与工程学报,1996,15(S1):511-514. NI Zhifang,LI Yumin.Theoretical calculation and regression on initial shock wave pressure of borehole in rock blasting[J].Chinese Journal of Rock Mechanics and Engineering,1996,15(S1):511-514. [7] 金旭浩,沙颖,王冉.柱状装药的爆破漏斗破坏分析[J].水利水电技术,2010,41(11):48-51. JIN Xuhao,SHA Ying,WANG Ran.Analysis on breakage from blasting crater of column charge[J].Water Resources and Hydropower Engineering,2010,41(11):48-51. [8] 王文龙.钻眼爆破[M].北京:煤炭工业出版社,1984. [9] HARRIES G.The modeling of long cylindrical charge of explosive[A].1st Int.Symp.on Rock Fragmentation by Blasting[C].Sweden,1983:419-431. [10] 卢文波.岩石爆破中应力波的传播及其效应研究[D].武汉:武汉水利电力大学,1994. LU Wenbo.The propagation of stress wave and its effects in rock blasting[D].Wuhan:Wuhan University of Hydraulic and Electric Engineering,1994. [11] HENRYCH J.爆炸动力学及其应用[M].北京:科学出版社,1987. [12] 宗琦.立井冻土掘进爆破参数模型试验研究[D].合肥:中国科学技术大学,2004. ZONG Qi.Tunneling blasting parameters model experiment study on vertical well freezing soil[D].Hefei:University of Science & Technology China,2004. [13] 马建军,熊祖钊,段卫东,等.工程爆破模拟试验的相似律[J].武汉科技大学学报(自然科学版),2001,24(2):170-174. MA Jianjun,XIONG Zuzhao,DUAN Weidong,et al.Theoretical testing study factors affecting parallel hole cut blasting[J].Journal of University of science and Technology (Natural Science Edition),2001,24(2):170-174. Initialshockpressureanalysisforholewallwithair-deckedcharge LOU Xiaoming1,2,WANG Zhenchang1,2,CHEN Bigang1,2,WANG Zuotang3,YU Jin4 (1.ZijinMiningCollege,FuzhouUniversity,Fuzhou350116,China; 2.InstituteforExplosiveTechnology,FuzhouUniversity,Fuzhou350116,China; 3.SchoolofMiningTechnology,ChinaUniversityofMiningandTechnology,Xuzhou221116,China; 4.InstituteofGeotechnicalEngineering,HuaqiaoUniversity,Xiamen361021,China) In order to analyze the initial shock pressure of hole wall with air-decked charge,the column charge is equivalent to a certain number of the spherical charges with Starfield method.Considering the attenuation and superposition of the pressure in the axial direction,the theoretical solution of the initial pressure acting on the hole-wall can be obtained for the charge conditions of up-air-deck and middle-air-deck,respectively.The stress monitoring is carried out with the numerical modeling by the software of ANSYS/LS-DYNA.Meanwhile,the stress field of explosion around the blast hole is also measured for the concrete model via the high-speed dynamic stress testing system.The comparison is conducted between the results obtained from the numerical measurements and theoretical solutions.Results show that the maximum stress occurs in the charging section for the up-air-deck charge condition.With the increase of the distance away from the charging section,the stress presents a sharp decrease first and maintains a relatively constant value.For the middle-air-deck condition,the minimum stress occurs at the middle of the air column and the maximum stresses occurs at the both end of borehole.The relative errors between the initial impact pressures obtained from the theoretical solution and numerical model are relatively small for both the two charging structures.The above mentioned results indicate that the pressure distribution is nonuniform along the axial direction of the borehole.Meanwhile,the stress distribution characteristics for the two charge structures agree well with the theoretical results,which verifies the rationality of the theoretical solutions. air-decked charge;initial shock pressure;numerical simulation;concrete model 楼晓明,王振昌,陈必港,等.空气间隔装药孔壁初始冲击压力分析[J].煤炭学报,2017,42(11):2875-2884. 10.13225/j.cnki.jccs.2017.0919 LOU Xiaoming,WANG Zhenchang,CHEN Bigang,et al.Initial shock pressure analysis for hole wall with air-decked charge[J].Journal of China Coal Society,2017,42(11):2875-2884.doi:10.13225/j.cnki.jccs.2017.0919 TD235.4 A 0253-9993(2017)11-2875-10 2017-07-04 2017-09-13责任编辑常 琛 国家自然科学基金资助项目(51679093,51374112) 楼晓明(1972—),男,浙江东阳人,副教授,博士。Tel:0591-22866516,E-mail:lxm@fzu.edu.cn1 理论基础
1.1 Starfield迭加法




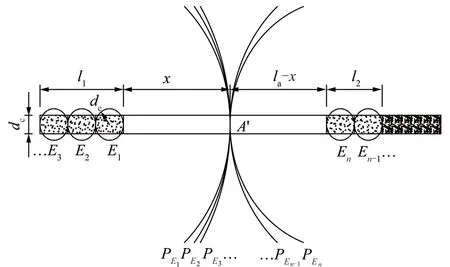
1.2 上部空气间隔装药孔壁初始冲击压力分析


1.3 中部空气间隔装药孔壁初始冲击压力分析



2 模型实验验证
2.1 应力测试原理及系统

2.2 混凝土模型及应变砖制作
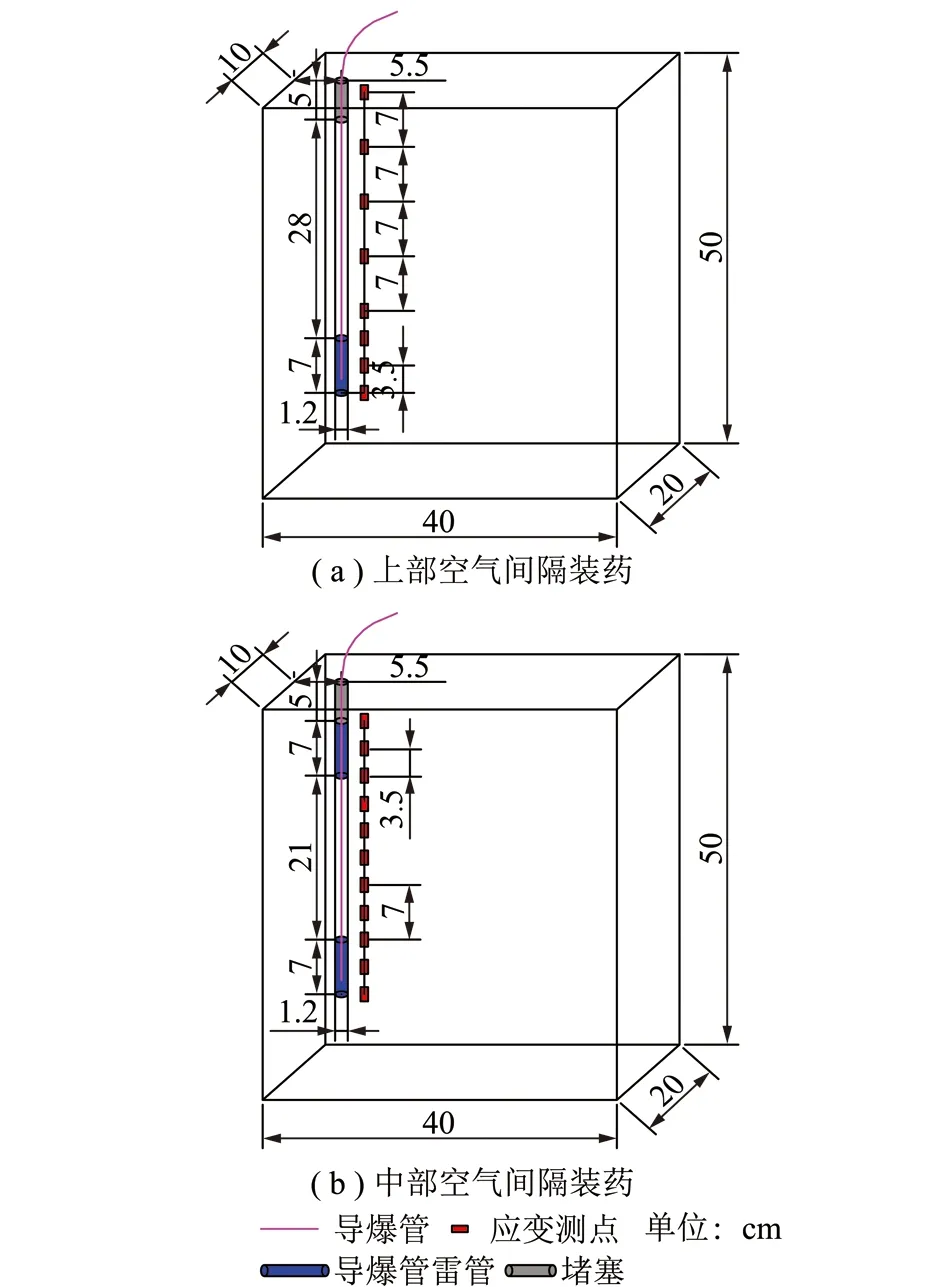
Table1Physicalmechanicsparametersofexperimentalmodal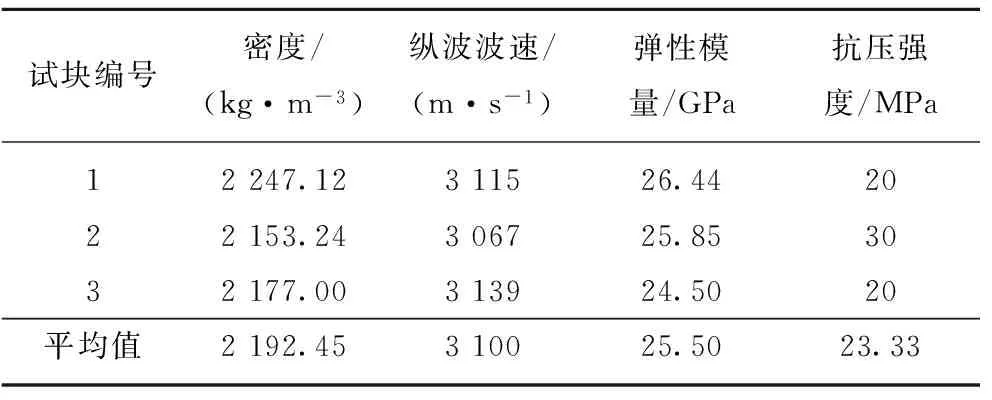
2.3 实验结果
Table2Stresstestresultswithup-air-deckchargestructureandmiddle-air-deckchargestructure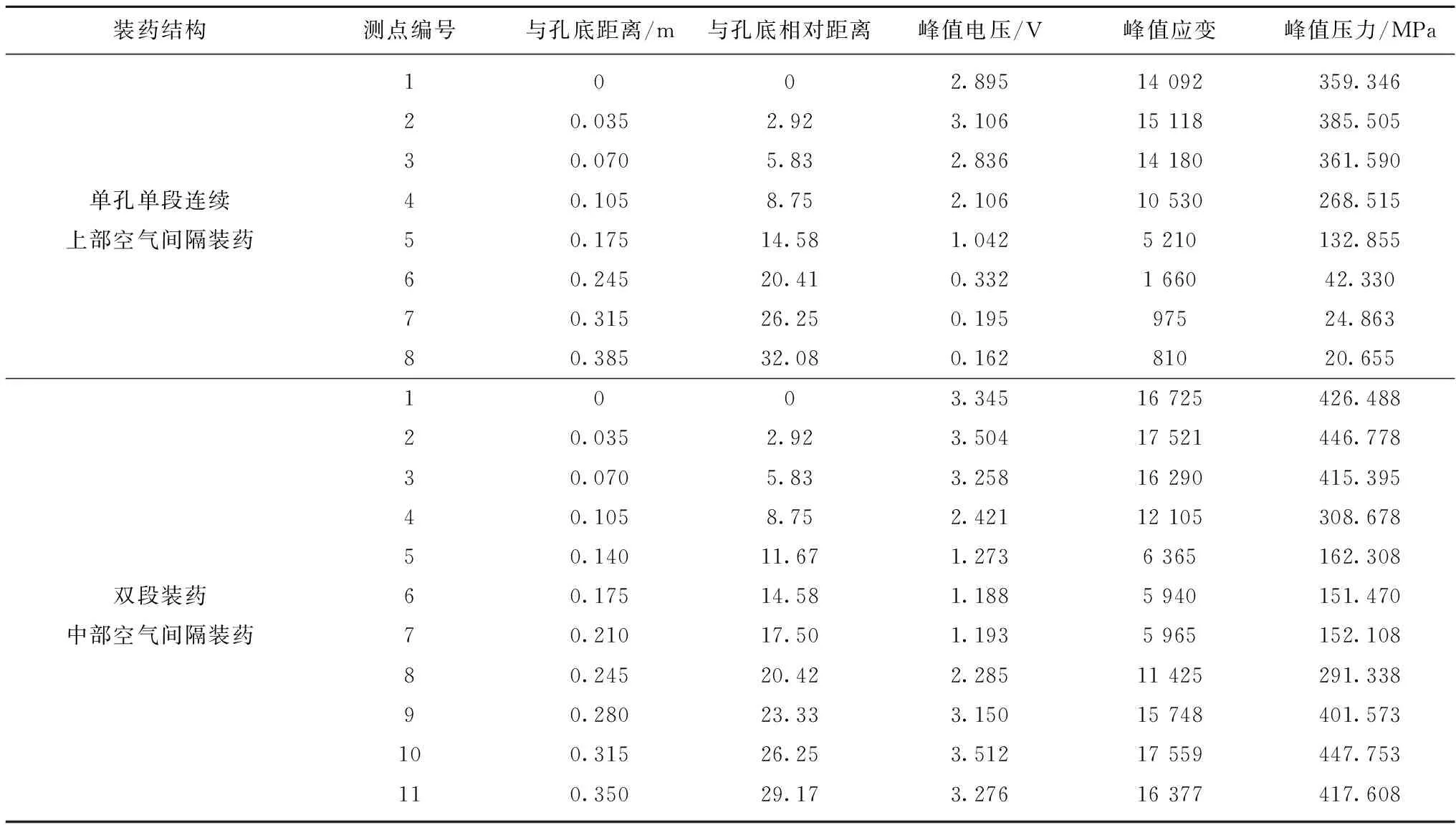
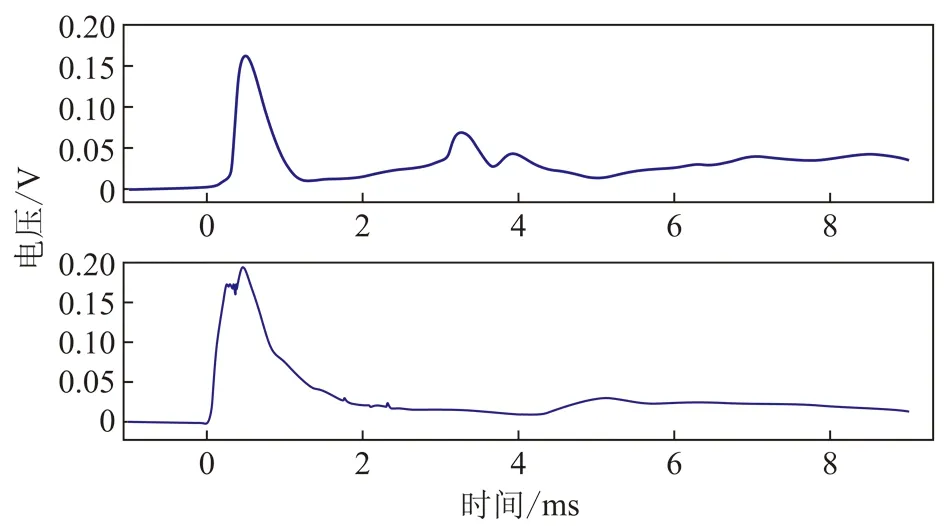
2.4 实验结果分析及讨论



3 数值模拟验证
3.1 孔壁初始冲击压力轴向分布特征分析
Table3Parametersettingofdifferentchargecondition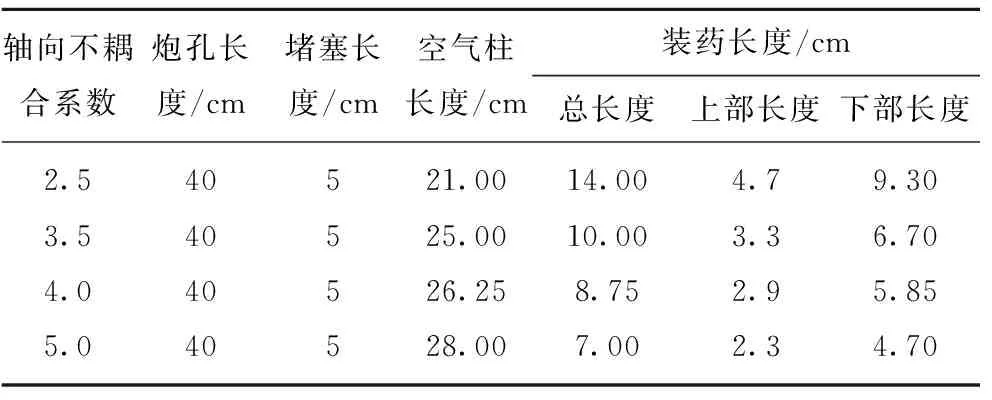
Table4Materialandstateequationparametersofrock
Table5Materialandstateequationparametersofexplosive
Table6Materialandstateequationparametersofair
Table7Parametersofthestemmingmaterialproperties
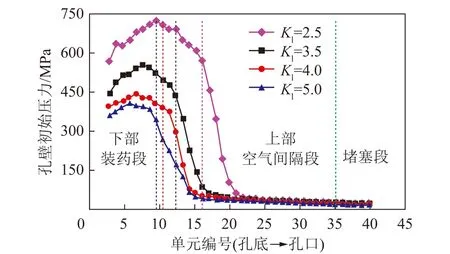

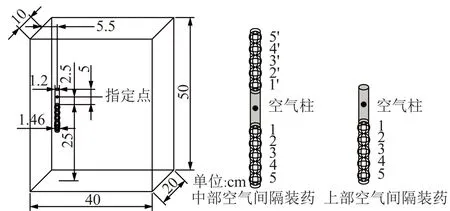
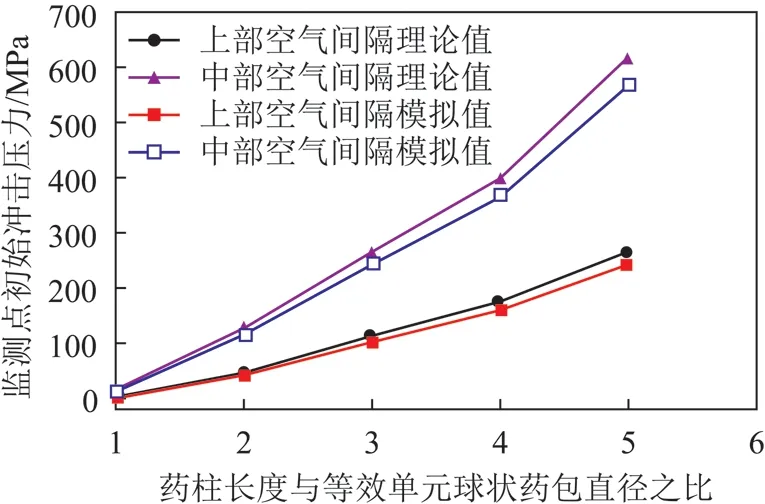
3.2 孔壁初始冲击压力理论公式合理性分析
4 结 论
