几何粗糙对岩体裂隙非线性流动的影响机制

朱红光，易 成，马宏强，张宇婷，苏振晋，褚 震，谢和平

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083; 2.四川大学，四川 成都 610065)

几何粗糙对岩体裂隙非线性流动的影响机制

朱红光1，易 成1，马宏强1，张宇婷1，苏振晋1，褚 震1，谢和平2

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083; 2.四川大学，四川 成都 610065)

破断岩体裂隙的几何粗糙使得其中的流体流动行为呈现出显著的非线性。借助粗糙裂隙的平行板离散模型和COMSOL软件，分析了离散模型单元体内部的流体流速及压力分布规律，获得了岩体裂隙中非线性流动产生的物理机制;研究了裂隙几何特征对非线性流动的影响规律，提出岩体裂隙非线性流动的流量计算方法，并与数值模拟结果进行了对比。结果表明:隙宽突变处的附加压力降损耗是导致粗糙裂隙流体流动产生非线性的主因;裂隙壁面粗糙和雷诺数的耦合作用显著影响裂隙中流体的非线性流动行为，裂隙中隙宽明显收缩处是附加压力降损耗的主要位置;提出的粗糙裂隙非线性流动的流量计算方法显著提高了分析结果的准确度，显示出较好的实用性。

裂隙粗糙;非线性流动;影响机制;附加压力降损耗

近年来，由于地下水及油气资源等的开采，破断岩体裂隙中的流体流动问题受到了极大的关注。由于裂隙能为地下流体的迁移提供通道[1-2]，油气、地热以及地下水等都适合在裂隙高度发达的岩层中开采[3]。因此理解和量化地下流体在岩体裂隙中的流动性质对这些资源开采的经济性非常关键。而现有研究表明流体在岩体裂隙中的流动行为呈现出复杂和非线性[4-5]:相同的隙宽，裂隙壁面粗糙的轻微变化就会导致流动路径的迂曲和传导能力的改变。而裂隙粗糙究竟是如何影响岩体中流体的流动行为仍未明晰，值得深入探讨。

以往众多学者研究了粗糙裂隙中的流体流动形态和非线性行为，多数是借助某个粗糙度参数如:裂隙面高度差[6-8]、节理面粗糙系数JRC[9-10]及分形维数D[11-12]等，来表征裂隙粗糙对非线性流动的影响，得到了很多经验的、试验的[13]或者数值模拟[14]的结果。这些结果均显示，随着雷诺数的增加，裂隙粗糙引起的非线性流动将越发明显。KONZUK等[15]通过一系列的试验和分析，指出只要雷诺数Re>1时粗糙裂隙就会出现非线性流动;DUSTIN等[16]借助数值模拟研究了裂隙粗糙与流体流态之间的关系，结果表明，高粗糙情况下裂隙中流体流动呈现出明显的迂曲路径，其导流系数与裂隙粗糙参数存在某种函数关系。笔者在之前的研究中[17]建立了粗糙裂隙低雷诺数(Re<10)流动的非线性模型，但是裂隙粗糙如何影响流体的非线性流动行为，特别是在雷诺数Re>10情况下粗糙裂隙非线性流动的物理机制并未研究。本文从粗糙裂隙中流体的压力变化入手，分析了裂隙粗糙对流体非线性流动的作用机制和影响规律;并定义了一个反映裂隙几何粗糙作用的附加压力降损耗系数，进而修正了本文的粗糙裂隙的流量计算公式。

1 粗糙裂隙单元体内流动模拟

本文之前的研究中[17]提出了粗糙裂隙的平行板离散模型，如图1(a)所示，图中实线代表原粗糙裂隙，虚线代表离散裂隙，该离散模型能够较好的表达出原裂隙的粗糙特征。因此，可以基于离散裂隙进行几何粗糙对非线性流动的影响机制探讨。从图1(a)中可以看出，原裂隙的粗糙在离散裂隙中表现为不同隙宽的小段平行板以某一角度联接;文献[4]的研究表明，平行板的连接角度对其中流体流动影响很小，可近似忽略。因此离散裂隙可用一系列无角度连接的平行板表示(图1(b))。文献[17]对粗糙裂隙的非线性流动研究表明，裂隙隙宽显著变化的位置，其压力降不服从立方定律，即小段平行板之间的隙宽突变会导致流动压力的非线性衰减。因此，可以从离散模型中取一个包含隙宽变化的典型代表单元体进行分析。

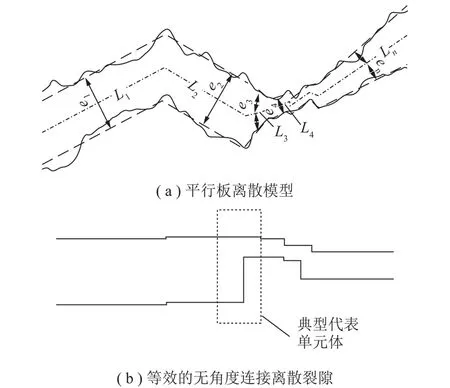
图1 粗糙裂隙的平行板离散模型Fig.1 Series-parallel discrete model for rough fracture

典型代表单元体的取法如图1(b)中的黑色虚框所示，为了体现裂隙粗糙的影响，选取隙宽不同且连通的两小段平行板为单元体。鉴于单元体上下面裂隙的组成方式是相同的，均为上下错动的平行板，只是错动的间距不同，而对流体非线性流动的影响是同一种作用，因此本文为了便于机制层面的探讨，取其一半为单元体进行分析，如图2所示，两段平板的长度相等，记为l/2;e1,e2分别为两段平行板的半隙宽。

想要从根本上研究几何粗糙对裂隙非线性流动的作用机制，就必须研究由隙宽突变引起的流体流动行为的变化。这在物理试验中难以观测，因此借助数值软件COMSOL Multiphysic模拟单元体在不同边界条件下的流体流动情况。数值分析时已知入口和出口压力，研究区域为两长方形。假设在平行板间流体温度为常数，密度也是常数，应用N-S方程描述该问题，且只进行水平方向的讨论，忽略重力的影响。主要的边界条件及参数设置见表1。

2 粗糙裂隙单元体的非线性流动机制

图3是在相同压力降下不同粗糙特征的单元体流线图，图中流线的颜色表示压力大小，从图3的上下图中都可以看出由于隙宽的扩张(e2比e1大)，流线不再保持原有的平行直线状态，发生了y方向的偏转，说明隙宽的扩张导致流体流速发生了改变;另外，对比上下图可知由于入口隙宽的不同(e1/l)，流线偏转程度也不同，入口隙宽的变化明显引起了流速的重分布。

表1边界条件和参数设置
Table1Boundaryconditionsandparametersforsimulation

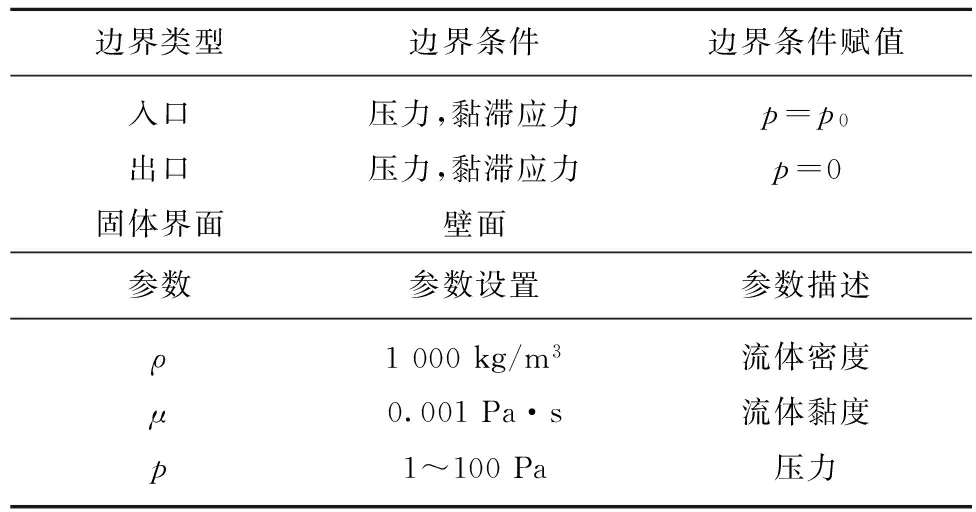
边界类型边界条件边界条件赋值入口压力,黏滞应力p=p0出口压力,黏滞应力p=0固体界面壁面参数参数设置参数描述ρ1000kg/m3流体密度μ0.001Pa·s流体黏度p1～100Pa压力

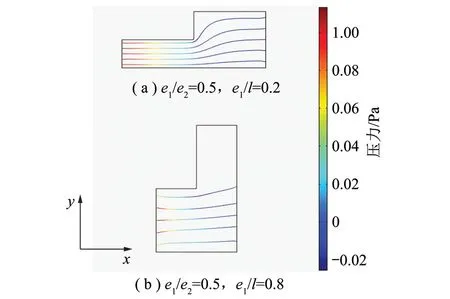
图3 单元体的流线图Fig.3 Streamline diagram of element

图4为e1/l=0.2时的压力分布，图中的颜色及纵向高度代表压力。可以看出在隙宽突变的位置附近，压力发生了较大的变化，先急剧减小，然后再变缓。若按照立方定律来分析，则压力变化应该如图中的黑色虚线所示，在隙宽突变处压力也会发生突变，但其下降的速率应该是不变的，为ab段的斜率。而实际上在隙宽突变附近真实的压力下降速率比黑色虚线大，导致在裂隙隙宽突变附近位置，压力降低的幅度比按局部立方定律大，即在相同流量的情况下，按立方定律计算得到的压力降会比实测小。这说明在局部立方定律计算时，隙宽突变的附近位置有一部分压力损耗被忽略了，这部分压力降称之为附加压力降损耗。因此，裂隙粗糙引起其中的流体流速重分布，从而引发附加压力降损耗是产生非线性流动现象的原因。

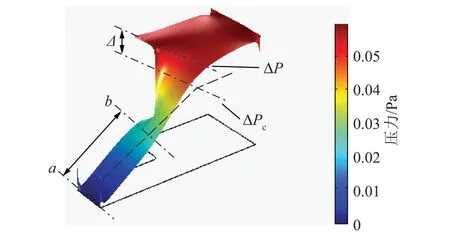
图4 e1/l =0.2的单元体压力分布Fig.4 Pressure distribution for element when e1/l=0.2

3 裂隙几何特征对非线性流动的影响规律

通过前面的分析可知，隙宽突变处的附加压力降损耗主要由2个因素引起:一部分是由隙宽突变处的流体流速变化所导致的;另一部分是由隙宽突变处的流体流动状态改变所导致的[18-19]。从上述原因可知，只要发生了隙宽突变则会引起附加压力降损耗，因此对多平行板等效模型单元体来说，就存在2种情况，即隙宽扩张和隙宽收缩，实际分析中单元体本身可以不变，只需改变流动方向即可表示这2种情况。本文就裂隙粗糙特征引起的附加压力降损耗进行分析，定义附加压力降损耗系数:

式中，ΔP为实测压力降；ΔPc通过局部立方定律计算得到的压力降，表示为

ΔPc=ΔP1+ΔP2

将式(2)代入式(1)，则有:

考虑到单元体入口的平均流速及雷诺数Re表示:

将压力降无量纲化:

则式(3)变成:

如果考虑图2的单元体中L1=L2=0.5l，则上式可以简化为

从上式可以看出，附加压力降损耗系数的影响因素有3个:裂隙粗糙参数e1/e2，e1/l;流动状态参数Re;以及压力降Δp。前两者是相互独立的，但后者与前两者均可能存在耦合关系。为了弄清楚3个因素之间的相互影响，对单元体在不同的e1/e2，e1/l;Re参数下进行数值分析，得到附加压力降损耗系数变化规律如图5～7所示。

图5 裂隙粗糙特征对附加压力降损耗系数的影响规律(Re=32)Fig.5 Effect of fracture geometry on the excess loss coefficient of pressure drop(Re=32)

图6 雷诺数对单元体附加压力降损耗的影响Fig.6 Effect of Re on excess pressure loss coefficient

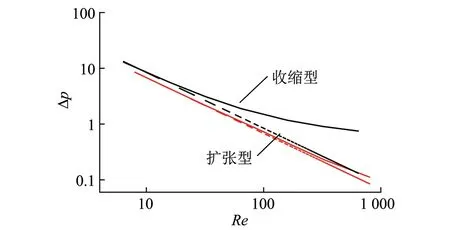
图7 无量纲的压力降Δp与雷诺数Re的关系Fig.7 Relationship of dimensionless pressure and Re

从图5可以看出，无论是扩张型还是收缩型，在e1/e2<0.5范围内，附加压力降损耗系数ξ变化较缓;当e1/e2>0.5随着比率的增大即单元体两平行板隙宽越接近，ξ快速下降;在e1/e2=1时单元体的两平行板连接为一个平行板，ξ为0。同时随着e1/l比率的增大即单元体两平行板的较小隙宽越接近特征长度，ξ越大。另外对比图5(a)和图5(b)可以看出，相同裂隙条件下，收缩型的附加压力降损耗显著大于扩张型。

图6为e1/l=0.2，e1/e2=0.5下，由式(7)得到的雷诺数Re对附加压力降损耗的影响。从图中可以看出，随着Re增大，ξ显著增加;很显然收缩型单元体较扩张型增加得更快。在Re达到300时，扩张型单元体的附加压力降损耗才10%，而收缩型则达到了惊人的60%，相比之下，扩张型的附加压力降损耗基本可以忽略。

另外由图6还可知，数据拟合所得扩张型附加压力降损伤系数与雷诺数呈线性增加的关系，这与式(7)中ξ-Re的反比例关系相差较大，说明式(7)中压力降Δp与其他参量存在耦合作用，对图6结果进一步分析，发现Δp与Re有如下关系，如图7所示。

图7中实线为数值模拟结果，虚线为拟合曲线。可以看出，压力降Δp随着雷诺数Re的增大而减小，将坐标轴取对数后发现，对于扩张型的单元体，其关系可以表示为

式中,C为Re=1时压力降，其值约为70。在对更大雷诺数Re=100,150,300,800,1 600求值后对比发现，上式的平均误差仅为10%，因此在估算ξ时，对于扩张型单元体，Δp×Re可直接用C代替。但对于收缩型单元体来说，上式的误差较大，Δp-Re双对数图约成二次下降的关系。在分析Δp×Re与Re的趋势后，发现有线性关系如图8所示。通过对多个e1/l的数据结果拟合，得到下式:

Δp×Re=0.61Re+14.04/(e1/l)

如此一来，综合式(8)～(10)就能直接求得裂隙单元体的ξ，分析粗糙裂隙中的非线性流动计算就会极大的简化。

图8 Δp×Re与Re的关系Fig.8 Relationship of Δp×Re and Re

上述关系和结论对自然粗糙裂隙的流体流动分析非常有意义，在分析裂隙粗糙引起的附加压力降损耗时应该关注隙宽较小并且是产生流动收缩效应的位置，其对整个流场中的附加压力降损耗起控制作用;同时，在附加压力降损耗系数中，首先考虑的几何参数是e1/l;而参考图5的规律，可近似将e1/e2<0.5的附加压力降损耗忽略，而e1/e2>5的情况直接用e1/e2=0.5的结果来代替，这无疑将大大简化自然粗糙裂隙水力传导能力的计算。

4 粗糙裂隙非线性流动的流量计算方法及应用举例

借助上节定义的附加压力降损耗系数，可以导出粗糙裂隙非线性流动的流量计算方法。在单元体内由式(1)可知

将式(2)代入上式，有

将上式推广到整个离散裂隙，有

式中，下标i表示第i个单元体。将上式变换一下，可以得到流量的计算公式:

这就是基于附加压力降损耗系数的粗糙裂隙非线性流动流量计算方法。附加压力降损耗系数可以通过上节所得到的式(5),(7)～(10)估算求得。

本文以岩石力学中典型的剖面粗糙曲线——JRC曲线来构建裂隙，选择较为粗糙的第6条JRC曲线与平行板组成裂隙6-P如图9中实线所示。其最小隙宽为0.51 mm，平均隙宽3.3 mm；裂隙长度100 mm，深度30 mm。主要有两个收缩区域，为虚框a,b部分。借助数值软件分析，在左端入口压力290 Pa作用下，通过该裂隙的流量为1.87×10-4m3/s。若采用立方定律的分析方法，将数据代入式(2)可求得流量Qc=2.36×10-4m3/s，与数值模拟结果相差达到了24%。作为对比，用式(12)进行计算，可只考虑隙宽收缩区域的过量压力降损耗，忽略扩张区域。将裂隙进行粗略离散，如图9中虚线示，收缩处离散成两段，利用公式(8)，(10)求得ξa=0.45,ξb=0.25，再代入式(12)可得到裂隙6-P的流量Qd=1.96×10-4m3/s，与数值模拟结果误差仅为4.8%，相比立方定律结果准确度提升了80%，说明本文计算方法具有较高的准确性。

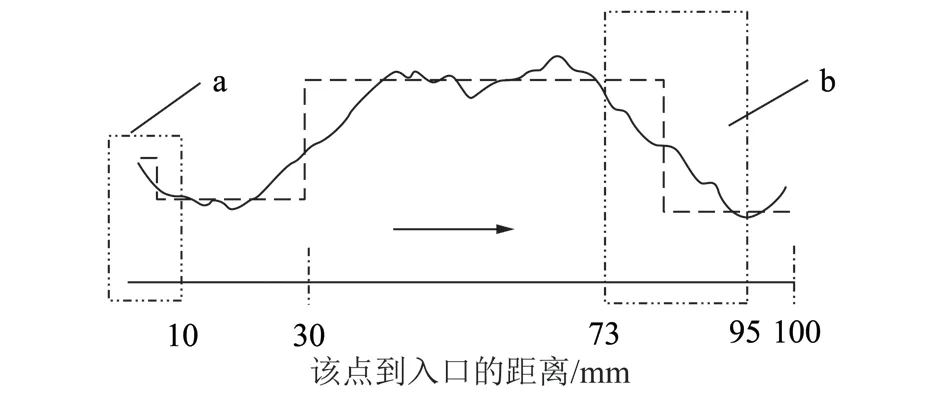
图9 裂隙6-P的离散示意Fig.9 Series-parallel equivalent of fracture 6-P

5 结 论

(1)裂隙粗糙引起其中的流体流速重分布，从而引发附加压力降损耗是产生非线性流动现象的原因。

(2)裂隙壁面粗糙和雷诺数的耦合作用显著影响裂隙中流体的非线性流动行为。提出了一个附加压力降损耗系数来表征裂隙几何粗糙特征对非线性流动的影响;该系数的关键影响参数为:裂隙单元体的几何参数e1/e2，e1/l，及雷诺数Re。随着e1/l比率的增大，单元体的附加压力降损耗显著增大;在保持e1/l不变的情况下，附加压力降损耗随e1/e2增大而减小;随着雷诺数的增加，附加压力降损耗显著增大;裂隙中隙宽显著收缩的位置附加压力降损耗较大，应予以特别关注。

(3)基于附加压力降损耗系数导出了粗糙裂隙非线性流动的流量计算方法，并就粗糙裂隙非线性流动的计算结果与数值模拟进行了对比。结果显示，基于附加压力降损耗系数的流量计算方法是正确有效的。

[1] LIU J,ELSWORTH D,BRADY B H.Linking stress-dependent effective porosity and hydraulic conductivity fields to RMR[J].International Journal of Rock Mechanics and Mining Sciences，1999，36(5):581-589.

[2] BRIAN Berkowitz.Characterizing flow and transport in fractured geological media:A review[J].Advances in Water Resources,2002,25(8):861-884.

[3] NEUMAN S P.Trends,prospects and challenges in quantifying flow and transport through fractured rocks[J].Hydrogeology Journal,2005,13(1):124-147.

[4] 朱红光,易成,姜耀东,等.裂隙交叉联接对采动岩体中流体流动特性的影响研究[J].中国矿业大学学报,2015,44(1):24-28.

ZHU Hongguang,YI Cheng,JIANG Yaodong,et al.Effect of fractures cross connection on fluid flow characteristics of mining-induced rock[J].Journal of China University of Mining & Technology,2015,44(1):24-28.

[5] 朱红光,谢和平,易成,等.破断岩体裂隙的流体流动特性分析[J].岩石力学与工程学报,2013,32(4):657-663.

ZHU Hongguang,XIE Heping,YI Cheng,et al.Analysis of properties of fluid flow in rock fractures[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(4):657-663.

[6] NOVAKOWSKI K S,LAPCEVIC P A,et al.Preliminary interpretation of tracer experiments conducted in a discrete rock fracture under conditions of natural flow[J].Geophysics Research Letters,1995,22(11):1417-1420.

[7] CARLSSON A,OLSSON T.The analysis of fractures,stress and water flow for rock engineering project[J].Analysis & Design Methods,1993,36(3):415-437.

[8] 王媛.单裂隙面渗流与应力的耦合特性[J].岩石力学与工程学报，2002，21(1):83-87.

WANG Yuan.Coupling characteristic of stress and fluid flow within a single fracture[J].Chinese Journal of Rock Mechanics and Engineering，2002，21(1):83-87.

[9] BARTON N,BANDIS S,BAKHART K.Strength,deformation and conductivity coupling of rock joints[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1985,22(3):121-140.

[10] OLSSON R,BARTON N.An improved model for hydromechanical coupling during shearing of rock joints[J].International Journal of Rock Mechanics and Mining Scienses,2001,38(3):317-329.

[11] WALSH J B.Effect of pore pressure and confining pressure on fracture permeability[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1981,18(5):429-435.

[12] 周创兵，熊文林.岩石节理的渗流广义立方定律[J].岩土力学，1996，17(4):1-7.

ZHOU Chuangbing，XIONG Wenlin.A generalized cubic law for percolation in rock joints[J].Rock and Soil Mechanics，1996，17(4):1-7.

[13] QIAN J,ZHAN H,ZHAO W,et al.Experimental study of turbulent unconfined groundwater flow in a single fracture[J].Journal of Hydrology,2005,311(S1-4):134-142.

[14] LI Z,WANG M,ZHAO J,et al.Analysis on intersections between fractures by parallel computation[J].International Journal of Coal Science & Technology,2014,1(3):356-363.

[15] KONZUK J S,KUEPER B H.Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture[J].Water Resources Research,2004,40(2):389-391.

[16] CRANDALL D,BROMHAL G,KARPYN Z T.Numerical simulations examining the relationship between wall-roughness and fluid flow in rock fractures[J].International Journal of Rock Mechanics and Mining Scienses,2010,47(5):784-796.

[17] 朱红光,易成,谢和平,等.基于立方定律的岩体裂隙非线性流动几何模型[J].煤炭学报,2016,41(4):822-828.

ZHU Hongguang,YI Cheng,XIE Heping,et al.A new geometric model for non-linear flow in rough-walled fractures based on the cubic law[J].Journal of China Coal Society,2016,41(4):822-828.

[18] 李卓,俞坚,马重芳.小通道单相流体突扩和突缩局部阻力特性[J].化工学报,2007,58(5):1127-1131.

LI Zhuo,YU Jian,MA Chongfang.Local resistances of single-phase flow across abrupt expansion and contraction in small channels[J].Journal of Chemical Industry and Engineering,2007,58(5):1127-1131.

[19] 孙琳,赵宝峰,郭春力.对圆管突然缩小局部阻力系数的研究[J].水利科技与经济,2010,16(4):367-368.

SUN Lin,ZHAO Baofeng,GUO Chunli.Study on local resistance coefficient of subcontract tube[J].Water Conservancy Science and Technology and Economy,2010,16(4):367-368.

Effectmechanismofgeometryroughnessonno-linearflowinrockfractures

ZHU Hongguang1,YI Cheng1,MA Hongqiang1,ZHANG Yuting1,SU Zhenjin1,CHU Zhen1,XIE Heping2

(1.SchoolofMechanicsandCivilEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China; 2.SichuanUniversity,Chengdu610065,China)

Geometry roughness of rock fractures affects the non-linear behavior of fluid flow through it.Com-bining with the series-parallel plate discrete model for rough fractures and COMSOL software,this paper analyzed the fluid flow velocity and pressure distribution in discrete model unit,and the physical mechanism of non-linear fluid flow occurred in fractures was obtained.By studying the law of geometry characteristic parameter effect on non-linear flow,a mass flow calculation method was proposed,and was compared with numerical results.It shows that the excess pressure loss taken place at aperture mutation position led to non-linear flow in rough fractures;it is the roughness of fracture wall coupled with Reynolds number which significantly influenced the non-linear flow behavior in rock fractures,and the max value of excess pressure loss arose in place which aperture obviously narrow;the proposed calculation method improved the analysis accuracy of results,displayed a better applicability.

rough fractures;non-linear flow;effect mechanism;excess pressure loss

朱红光，易成，马宏强,等.几何粗糙对岩体裂隙非线性流动的影响机制[J].煤炭学报,2017,42(11):2861-2866.

10.13225/j.cnki.jccs.2016.1412

ZHU Hongguang,YI Cheng,MA Hongqiang,et al.Effect mechanism of geometry roughness on no-linear flow in rock fractures[J].Journal of China Coal Society,2017,42(11):2861-2866.doi:10.13225/j.cnki.jccs.2016.1412

TD315

A

0253-9993(2017)11-2861-06

2017-01-10

2017-08-12责任编辑常 琛

北京市自然科学基金资助项目(8164061);国家自然科学基金资助项目(51578539);国家重点研发计划资助项目(2016YFC0600704)

朱红光(1984—)，男，湖南双峰人，副教授，博士(后)。E-mail:uu_gr@qq.com