关于对p级数敛散性研究的注记
2017-12-22张国利杜智慧
张国利, 杜智慧
(洛阳师范学院数学科学学院,河南洛阳 471934)
关于对p级数敛散性研究的注记
张国利, 杜智慧
(洛阳师范学院数学科学学院,河南洛阳 471934)
对于p级数收敛性,一般教材只给出了其随参数p的收敛性和发散性.本文归纳总结了p级数中当参数p取1, 2, 3时的特殊情况下的研究历史及一般情况下的推广.
p级数;调和级数;巴塞尔问题;阿佩里常数;zeta函数
在p级数的教学过程中,很多教材都只给出了其敛散性的结论,对于各种情况下的敛散性研究过程却没有深入研究,本文尝试对这个问题进行了一些探索.
我们把数项级数
(1)
称为p级数,也称超调和级数. 由积分判别法知, 当p>1时级数(1)收敛,p≤1时级数发散[1].
1 黎曼zeta函数
一般情况下,称
(2)
为黎曼zeta函数,其中s为实部大于1的复数[2]. 由此可知某些情况下(1)是(2)的特例. zeta函数是数学中很重要的函数,它在解析数论中有着极其重要的地位, 尤其是与素数的分布有着密切的联系,它在物理学、概率论和应用统计学中也有广泛应用.当s取值负整数时,欧拉[3]首先证明了此时ζ(s)为有理数,并指出了它在模形式理论中的重要作用.
ζ(s)的一个积分表达式为
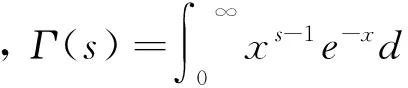
当s取正偶数2n时,ζ(2n)有一个简洁的表达式,即
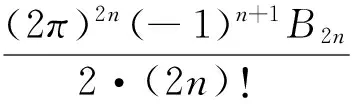
由上式,我们可以计算出ζ(2)、ζ(4)、ζ(6)、ζ(8)等数值,当s=-n,n为非负整数时,
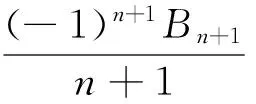
其中Bn为伯努利数,Bn用生成函数定义为
zeta函数与素数分布的密切关系体现在欧拉发现的恒等式中.
(3)
(3)式右端称为欧拉乘积.由于s=1时,(3)式左端发散,由此可知素数有无穷多个.
1859年,黎曼证明了zeta函数满足黎曼方程
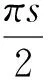
此处Γ(s)表示gamma函数.这个方程将s取负奇整数和正偶整数的zeta函数值联系了起来. 同时,他还提出了ζ(s)的零点分布假设,即著名的黎曼猜想,这也是克雷数学研究所悬赏的世界七大数学难题之一.
2 调和级数
当(2)式中s=1时,称级数
(4)
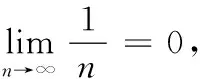
假设(4)收敛,设其和为S,则
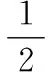
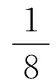
因为对任意的x>1,都有
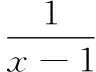
所以
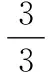
这就推出了矛盾,所以级数(4)发散.
此后,Honsberger,Leonard Gillman,Cusumano,Ecker等人也各自用不同的方法证明了(4)的发散性[4]. (4)的发散速度是很慢的,计算可得此级数的前1043项之和也不会超过100. 数学家欧拉曾证明(4)的前k项和只有一个对数级的增长速度,进一步,他还证明(4)中的n替换成素数后级数依然发散.
与(4)相关的一个级数是
(5)
称之为交错调和级数,通过莱布尼茨判别法容易证明(5)是收敛的.在1650年Mengoli证明了
上述等式也可以在对数函数ln(1+x)的泰勒级数展开式中令x=1得到.特别地,Hudelson在2010年用图形化的方法无字证明了此结论[5].
3 巴塞尔问题
当(2)式中s=2时,称级数
的求和问题为巴塞尔问题. 这个问题是数论中的一个重要问题,由Mengoli在1644年提出.1735年,年仅28岁的欧拉得到了经典的结果
(6)
并由此在数学界声名大振.欧拉采用的方法如下[6].
由sinx的麦克劳林级数得
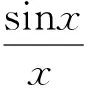
(7)
又因为
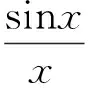
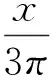
(8)
由(7) , (8)两式,比较x2的系数得
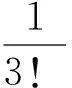
由此即得(6)式成立.
欧拉在证明的过程中默认(8)式的分解式是唯一的,这是未加证明的结论.事实上,在100年之后数学家维尔斯特拉斯才给出严格证明,称之为维尔斯特拉斯分解定理. 一直到1741年,欧拉才另外给出了一个严格的证明.更多严格的证明可以借助傅里叶级数、复分析和多元函数微积分等知识来给出.1821年,数学家柯西没有借助高等数学知识,仅用一元函数极限等知识给出了这个结论的初等证明[7].
由于
所以要想证明(6)式成立,只需证明
成立,历史上对(6)式的若干证法都是基于上式. 2003年,Robin Chapman总结了证明了(6)式的14余种方法.
正是受欧拉等数学家对此研究工作的影响,数学家黎曼在1859年定义了zeta函数这个非常重要的数学概念, 并给出了这个函数的一些基本性质.
4 阿佩里常数
当(2)式中s=3时,称级数和
(9)
为阿佩里常数,它是数论和特殊函数等交叉学科中一个非常重要的数,在电磁学、量子电动力学和随机最小生成树等数学物理问题中有重要应用.
Apéry在1979年证明了(9)是一个无理数,此证明被称之为Apéry定理.Apéry的证明十分复杂和难懂,Beukers和Zudilin分别在1979和2002年给出了更简洁的证明[8-9],但是至今为止还不知道(9)是否是一个超越数.
早在1772年,欧拉就给出阿佩里常数的级数表达式
(9)式还有很多经典级数表达式如
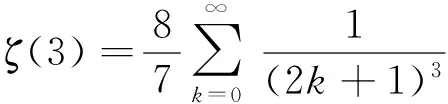
等或积分表达式如
许多数学家都试图推广Apéry的方法来证明ζ(2n+1)的无理性.2000年Rivoal 和Tanguy 证明了ζ(2n+1)中有无穷多个无理数.2001年,Wadim 和Zudilin证明了ζ(5),ζ(7),ζ(9),ζ(11)这四个数中至少有一个是无理数[10].
5 结语
在对p级数这一知识点的教学过程中,通过对参数p=1, 2, 3等特殊值的研究过程的讲解以及对相关数学家的介绍,可以使学生加深对这些结论的认识,从而增加学习兴趣,活跃课堂气氛.
[1] Vladimir Z A. Mathematical Analysis I [M]. Germany: Springer, 2004: 96-100.
[2] Edwards H M. Riemann’s Zeta Function[M].American:Dover, 2001.
[3] Dunham W. Euler: The Master of Us All[M]. American:The Mathematical Association of America, 1999.
[4] Steven J. The Harmonic Series Diverges Again and Again[J].The Amatyc Review, 2006, 27: 31-43.
[5] Hudelson, Matt.Proof Without Words:The Alternating Harmonic Series Sums to ln 2[J]. Mathematics Magazine, 2010, 83 (4): 294.
[6] Sandifer, Charles Edward. How Euler Did It[J]. Mathematical Association of America, 2007: 193.
[7] Robin Chapman. Evaluating ζ(2)[EB/OL].2003:http://empslocal.ex.ac.uk/people/staff/rjchapma/etc/zeta2.pdf
[8] Beukers F. A Note on the Irrationality of ζ(2) and ζ(3)[J]. Bull. London Math. Soc, 1979,(11): 268-272.
[9] Zudilin W.An elementary proof of Apery’s theorem[EB/OL].2002: https://arxiv.org/pdf/math/0202159.pdf
[10] Zudilin W. One of the numbers ζ(5), ζ(7), ζ(9), ζ(11) is irrational[J]. Russ.Math. Surv, 2001, 56 (4): 774-776.
A Note on the Research of thep-series’ Convergence and Divergence
ZHANG Guo-li, DU Zhi-hui
(College of Mathematics and Science, Luoyang Normal University, Luoyang 471934, China)
When teaching the convergence and divergence of thep-series, many mathematical analysis textbooks only provide the convergence and divergence with the parameterp. This paper summarizes the research history and the main conclusion whenpis 1, 2 and 3 and their generalizations.
p-series; harmonic series; Basel problem; Apery constant; zeta function
O173
A
1009-4970(2017)11-0022-03
2017-06-08
张国利(1978—), 男, 河南温县人, 讲师.
[责任编辑 胡廷锋]
